新体制机载雷达波形优化设计研究综述

李志汇, 唐 波, 周青松, 师俊朋, 张剑云

(国防科技大学电子对抗学院, 安徽 合肥 230037)

0 引 言

在现代复杂战场环境中,战场态势瞬息万变,如何及时、准确、全面地获取战场态势信息是夺取战争胜利的关键因素。机载雷达借助飞机平台的高度可以克服地球曲率的影响,扩大了对空中、海上和陆地上各类低空和超低空目标的探测距离,机载雷达是夺取战场主动权和赢得胜利的关键因素之一[1]。机载雷达利用空时自适应处理(space time adaptive processing, STAP)技术,根据目标和杂波在空间-多普勒域上的分布差异对杂波进行抑制,可以提高慢速目标的检测能力[2-6]。自1973年Brenann和Reed首次提出STAP理论以来[2],经过学者们四十多年的探索和研究,STAP技术已经形成了比较成熟和完善的理论体系,而且是当前国际雷达领域的研究热点[7-12]。

然而,传统关于机载雷达杂波抑制和运动目标检测的研究,大都基于雷达发射固定形状的脉冲序列,在接收端进行STAP处理来检测运动目标[7-12],而复杂电磁环境下机载雷达面临的战场环境瞬息万变,传统发射固定波形的方式使得机载雷达无法有效完成复杂电磁干扰环境和高动态杂波环境下对低空、隐身等目标的检测、跟踪等任务。此外,随着无线通信技术和雷达技术的快速发展,战场上电子设备的种类也越来越多,电子设备与机载雷达的频段相互重叠,严重影响机载雷达的工作性能[13-14]。因此,为提升机载雷达面对隐身/低空目标、复杂电磁对抗环境以及高动态杂波环境的探测性能,扩展机载雷达对空和对地海一体化监视的功能,使机载雷达融入现代化信息作战体系并成为核心的网络战枢纽,必须发展新体制机载雷达、新体制机载雷达杂波及干扰抑制等新技术。

认知雷达和多输入多输出(multiple-input multiple-output, MIMO)雷达的出现为解决上述问题提供了一条崭新的途径。认知雷达充分利用了目标与环境信息,将STAP从接收端延伸到了发射端,构成了接收机、发射机与环境动态闭环的全自适应雷达处理系统[15-18]。认知雷达能够根据动态环境数据库中的先验信息以及雷达实时获取的目标及环境信息推理决策适合当前雷达工作场景的最优波形和信号处理参数,自适应地调整优化雷达系统资源配置和发射信号波形,从而适应复杂多变的工作环境,实现对目标的最佳探测效果。MIMO雷达是近年来发展起来的一种新体制雷达,引入多天线、多波形收/发技术和概念,通过发射多个独立的波形/信号(即波形分集特性)来获得波形分集增益[19-23]。MIMO雷达分为集中式MIMO雷达和统计MIMO雷达,收发天线分置的统计MIMO雷达通过空间分集增益可以克服目标散射截面积起伏所带来的性能损失[21]。与传统的相控阵雷达相比,MIMO雷达具有以下优势:杂波及干扰抑制能力强[24-25];参数估计精度高[26-28];抗干扰能力强[29-30];反隐身能力强[21];反侦察、低截获性能高[31];抗摧毁能力强。

随着灵活波形产生器和高速信号处理硬件的快速发展,雷达发射复杂的波形以动态适应其所面临的感知环境成为了可能[32]。作为认知雷达的关键技术之一,近些年来,认知雷达波形优化设计,尤其是信号相关杂波或干扰背景下的认知雷达波形优化设计,受到了国内外学者的广泛关注[33-45]。从目标检测的角度,认知雷达波形优化设计就是以最大化目标的检测性能为优化准则,同时考虑发射波形的实际约束条件,吸收借鉴先进的优化方法,来设计发射波形或接收滤波器。但机载雷达由于平台架设高以及平台运动,其回波模型不同于传统地基雷达。此外,机载雷达面临的杂波环境是非均匀和非平稳的,高脉冲重复频率下还存在杂波的距离模糊问题,这也不同于地基雷达。考虑机载平台的特殊性,将认知理论与机载MIMO雷达相结合,充分利用MIMO雷达发射波形的自由度,结合动态环境的先验信息,开展机载MIMO雷达发射波形优化设计或发射波形与接收滤波器联合设计,对于提升机载MIMO雷达在复杂电磁对抗环境以及高动态杂波环境下的目标检测性能而言具有重要意义,也为机载认知雷达系统的发展提供了理论支撑。

本文介绍了当前新体制机载雷达波形优化设计的研究进展。具体而言,阐述了认知雷达的基本原理,对新体制机载雷达波形优化设计进行了概述;从先验条件是否理想以及收发处理的角度,对机载雷达波形优化设计的研究成果进行了总结归纳,在此基础上进行总结和分析,针对当前机载雷达波形优化设计存在的问题,对新体制机载雷达波形优化设计的未来研究趋势进行了展望。

1 认知雷达原理与新体制机载雷达波形优化设计概述

1.1 认知雷达原理

认知雷达继承了从发射到接收的联合全自适应处理架构[15],其原理如图1所示。

图1 认知雷达工作原理框图Fig.1 Diagram of principle of cognitive radar

可以看出,雷达与目标、环境构成了闭环处理系统,系统通过与外界环境不断地交互实现对环境的感知。首先,系统通过实时雷达场景分析获取环境中目标、杂波和噪声的统计特性和不确定性,统计特性实现了对环境的精细化表征,不确定性决定了先验信息的准确程度,不确定度越小,先验信息越准确,反之亦然。然后,利用场景分析结果并结合环境动态数据库对接收回波进行实时分析,根据系统的任务确定优化准则,包括目标检测、参数估计、目标识别和抗干扰性能等。最后,系统利用反馈信息和先验知识,并在现有优化准则和波形约束条件下设计最优发射波形,实现与当前目标和环境的最佳匹配。

这种感知—优化设计—自适应调整的闭环探测系统最大程度地利用了先验信息和实时环境信息,通过波形优化设计使雷达“主动”适应环境的变化,而不是接收机“被动”地自适应,从而大大提升了系统的性能。具体地,雷达通过环境动态数据库和环境感知模块实时感知外界杂波环境、干扰环境以及电磁散射特性的变化,获取杂波、干扰以及电磁散射特性的特征和先验参数;然后,波形优化模块利用环境动态数据库和环境感知模块获取先验信息,根据雷达系统的目标任务以及系统对波形的实际约束条件,设计最优的发射波形或者联合设计发射波形与接收滤波器,使得所设计的波形和接收滤波器具有最优的杂波和干扰抑制性能、最优的目标检测、估计和识别性能。

1.2 新体制机载雷达波形优化设计概述

将认知雷达原理运用于机载雷达,使机载雷达拥有感知环境信息的能力,从而实现目标特性、杂波和干扰变化时的目标检测、估计和识别性能优化。由认知雷达工作原理可知,波形优化设计是其中的关键环节,开展新体制机载雷达波形优化设计研究不仅要关注雷达发射机硬件技术(如任意波形发生器和智能发射机),还要研究与之相适应的波形优化设计方法。新体制机载雷达波形优化设计的基本过程为:充分利用目标、杂波和干扰的先验信息,根据机载雷达目标检测、参数估计或识别等任务确定优化准则,同时考虑雷达硬件资源约束(即波形约束),采用合适的先进优化方法来设计发射波形(与接收滤波器),以提升复杂场景下机载雷达的工作性能。因此,先验信息、优化准则、约束条件是构成新体制机载雷达波形优化问题的三个要素,优化方法是解决波形优化设计问题的关键。

(1) 目标、杂波和干扰的先验信息通过动态环境数据库(包括:地理信息系统、先前的扫描跟踪、电磁反射、杂波谱模型等)获取。在实际非理想条件下,由于估计误差、动态时变的杂波环境以及复杂多变干扰的存在,先验信息并不是完全准确的,如何在非理想先验条件下设计发射波形(与接收滤波器)以抵抗先验信息的失配是值得关注的问题。

(2) 优化准则与机载雷达的任务有关。衡量检测性能的优化准则一般采用最大化输出信干噪比(signal to interference-plus noise ratio, SINR)或信杂噪比(signal to clutter plus noise ratio, SCNR)作为优化准则,当先验信息不准确时,通过设计最差性能输出SINR或SCNR作为优化准则。衡量参数估计性能的优化准则一般采用最小化克拉美罗界(Cramer-Rao bounds, CRB)或者最大化互信息(mutual information, MI)作为优化准则。雷达接收回波与目标冲激响应之间的互信息越大,目标的估计性能越好; 无偏估计下目标的CRB越小,参数估计性能越好。如何建立上述评价准则与雷达发射波形之间的关系,是开展波形优化的前提。

(3) 波形约束主要与雷达发射机硬件的物理可实现性有关,工程实际波形中一般考虑能量约束、恒模约束、峰均比(peak-to-average power ratio, PAPR)约束和相似性约束。其中,能量约束用于约束发射波形的能量不至于过大,恒模约束和PAPR约束对于射频功率放大器而言能够避免不必要的非线性影响,相似性约束可使发射波形具有良好的脉冲压缩和模糊函数特性。此外,在频谱拥挤情况下,还需考虑波形的频谱约束,使机载雷达避开通信系统的工作频段。

(4) 机载雷达波形优化问题是一个包含多变量和多约束条件的非线性高维优化问题,波形优化方法的设计要考虑实际优化问题的数学特征、雷达硬件性能要求以及系统响应时间等。

2 新体制机载雷达波形优化设计研究现状

新体制机载雷达波形设计的关键就是如何根据目标、杂波/干扰等先验信息实现最优目标检测和参数估计。因此,在给定波形优化设计的优化准则和约束条件后,目标、杂波/干扰等先验信息的准确性极大程度地影响着波形设计的效果。当先验信息准确时,机载雷达能够自适应地设计与目标匹配、与杂波/干扰失配的发射波形,以提升系统目标检测与参数估计的性能;当先验信息不准确时,所设计的波形必然与实际工作环境失配,导致系统性能严重恶化。此外,实际机载MIMO雷达阵列中不可避免地存在各种误差,当误差存在时,不仅导致理想的空时响应产生畸变,而且严重影响雷达系统的检测性能。本文将先验信息准确和误差不存在统称为理想条件,将先验信息不准确和误差存在统称为非理想条件,并分别从先验条件理想和先验条件非理想的角度,详细介绍新体制机载雷达波形优化设计的研究进展。

2.1 先验条件理想时机载雷达波形优化设计

根据阵列天线配置,雷达可以分为单输入单输出(single-input-single-output, SISO)雷达和MIMO雷达;根据收发处理方式,分为仅发射端的波形设计和收发(指发射波形和接收滤波器)联合设计;根据杂波和干扰模型与发射波形的关系,可以分为信号相关杂波或干扰、信号无关杂波或干扰;根据发射信号的形式,可以分为线性调频(linear frequency modulated, LFM)波形、正交频分复用(orthogonal frequency division multiplexing, OFDM)波形、MIMO正交频分复用(MIMO orthogonal frequency time division multiplexing, MIMO-OFDM)和步进频波形等。因此,新体制机载雷达波形优化设计的研究内容多种多样,下面从收发处理的角度对先验条件理想时机载雷达波形优化设计的研究进行总结。

2.1.1 机载雷达发射波形优化设计

2010年,De Maio等[46]给出了色高斯杂波场景下机载雷达波形优化的信号模型,将杂波背景下的目标检测问题表示为二元假设检验问题,表达式为

(1)

(2)

2011年,文献[47]较早地研究了色高斯干扰下多输入多输出(multiple-input multiple-output space time adaptive processing, MIMO-STAP)波形优化方法,以提升MIMO-STAP的目标检测性能。其中,波形相关的接收信号模型可以表示为

(3)

(4)

式中:P表示总的发射功率。文献[47]将问题(4)转化为SDP问题进行求解,仿真结果表明该方法能够有效提升输出SINR。然而,该方法的对角加载因子随着杂噪比(clutter-to-noise ratio, CNR)的增加而增加,使得所设计的波形协方差矩阵偏离最优值而无法充分抑制强杂波。为此,Tang等[48]提出了一种不需要对角加载的波形优化方法来优化波形协方差矩阵,该方法避免了杂波协方差矩阵的启发式对角加载,且能够寻得全局最优值。进一步地,Tang等[49]提出一种计算高效的算法来优化MIMO-STAP的波形,该算法迭代优化接收滤波器和发射波形。结果表明,这种方法不仅能够获得期望的输出SINR,而且其计算复杂度远小于文献[48]所提方法。

图2给出了文献[48]中不同波形的输出SINR随阵列信噪比(array signal to noise ratio, ASNR)和CNR的变化,可以看出,文献[47]和文献[48]方法得到的优化波形优于正交波形和单输入多输出波形。从图2(a)可以看出,当ASNR比较大时,文献[47]方法无法获得最优波形,导致其SINR性能明显低于文献[48]方法。从图2(b)可以看出,文献[47]方法的输出SINR随CNR的增加而显著下降,这是由于文献[47]的方法随着CNR增加而对角加载因子增大,导致所设计的波形越来越偏离最优波形。图3给出了文献[48]和文献[49]方法的输出SINR和计算时间,可以看出,尽管文献[49]方法的输出SINR略低于文献[48]方法,但是前者的计算时间远小于后者。

图2 不同方法的输出SINR性能(文献[47]及文献[48]所提方法)Fig.2 Output SINR performance of different methods ([47] and [48])

图3 不同方法的输出SINR性能能(文献[48]及文献[49]所提方法)Fig.3 Output SINR performance of different methods ([48] and [49])

2014年,Sen[50]研究了机载正交频分复用-空时自适应处理(OFDM-STAP)雷达PAPR约束下的波形设计问题,该方法以最大化SINR、最小化归一化空域频率和多普勒频率的CRB以及目标散射稀疏估计的CRB矩阵作为4个目标函数,建立了多目标优化问题,并采用非支配排序遗传算法II进行求解。机载OFDM-STAP接收信号模型为

(5)

式中:A是一个包含发射信号权值的复对角矩阵;XT和XC,k分别表示包含目标和第k个方位角杂波散射系数的对角矩阵;Φ和Φk分别表示目标和杂波空时导向矩阵;N表示噪声,关于A,XT,XC,k,Φ和Φk的具体表达详见文献[50]。实际上,由于目标不同的散射中心在不同的频率下产生不同的共振,通过机载OFDM雷达可以提供额外的信息,从而增加了系统的频率分集特性,提升了杂波背景下的目标检测性能。图4给出了文献[50]中两种场景下不同波形的检测概率随信噪比(signal to noise ratio, SNR)的变化,尽管固定OFDM波形的检测概率低于时域码和巴克码,但是文献[50]得到的自适应OFDM波形具有最优的检测性能。文献[51]研究了恒模约束下MIMO-OFDM雷达的波形优化问题,与文献[47]中的方法类似,该方法从接收数据中估计所需参数时,仍然会存在性能下降的问题。

图4 不同波形的检测概率随SNR的变化Fig.4 Detection probability of different waveforms versus SNR

2015年,文献[52]研究了机载MIMO雷达发射方向图的设计方法,以解决非均匀杂波背景下的旁瓣杂波抑制问题,该方法以最大化空时匹配滤波后的输出SCNR为优化准则,同时约束发射波形,使其在主瓣方向具有一定的增益,以此来抑制旁瓣区域的杂波能量来提高输出SCNR。进一步地,为了解决杂波抑制下的发射方向图优化与目标检测之间的矛盾,将发射阵列分为杂波抑制子阵和目标检测子阵,提出基于子阵划分算法和最优探测子阵发射方向图的设计方法[53],实现了对杂波环境的实时感知探测。

文献[54]采用接收信号和目标脉冲响应之间的互信息作为优化准则,通过波形优化来提升运动目标的检测性能,基于最大化互信息的波形优化问题可表示为

(6)

式中:Rtc表示目标加杂波协方差矩阵;Rc和Rn分别表示杂波和噪声协方差矩阵,Rtc,Rc和Rn的具体表示详见文献[54]。为解决波形优化问题(见式(6)),文献[54]利用极大极小(majorization-minimization, MM)算法和交替方向乘子算法(alternation direction method of multipliers, ADMM)寻找最优波形。图5给出了文献[54]中不同波形的互信息和检测概率随总发射功率的变化。

图5 不同波形的互信息和检测概率对比Fig.5 Comparison of mutual information and detection probability for different waveforms

由图5可以看出,文献[54]的方法利用了目标和杂波的先验信息,可以获得最大的互信息,因此具有最佳的检测性能。

2.1.2 机载雷达发射波形和接收滤波器联合优化设计

发射波形和接收滤波器的联合优化设计涉及收发联合优化,在此框架下,机载雷达接收的目标和杂波是信号相关回波,即是发射波形经过目标和杂波调制后产生的与发射波形具有很强相关性的回波。2016年,Tang等[55]较早研究了机载MIMO雷达发射波形和接收滤波器联合设计问题,图6给出了机载MIMO雷达阵列几何结构示意图,机载MIMO雷达波形相关回波模型可以表示为

y=αt[IM⊗INR⊗ST][u(fd)⊗b(θt)⊗a(θt)]+

[u(fc,l,k)⊗b(θc,l,k)⊗a(θc,l,k)]+yj

(7)

式中:αt和αc,l,k分别表示目标和第l个距离单元第k个杂波块的复幅度;u(f)、a(θ)和b(θ)分别表示时域导向矢量、发射空域导向矢量和接收空域导向矢量;S为系统波形矩阵;Jl表示转移矩阵;yj为噪声部分。

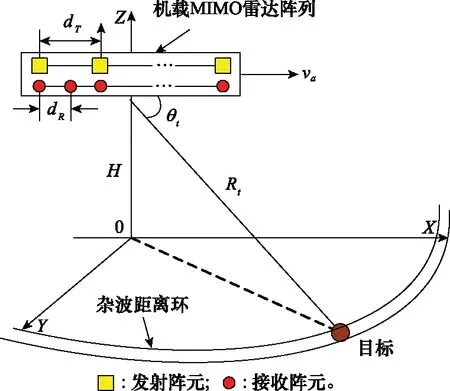
图6 机载MIMO雷达阵列几何结构Fig.6 Geometry configuration of airborne MIMO radar

接收信号通过接收滤波器w处理,考虑波形的能量约束,MIMO-STAP发射波形和接收滤波器联合优化设计问题可以通过最大化输出SINR得到:

(8)

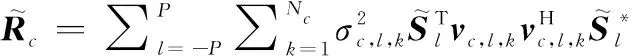
图7 不同算法的输出SINR随目标归一化多普勒频率的变化Fig.7 Output SINR of different algorithms versus the normalized Doppler frequency of the target

通常而言,机载MIMO雷达发射波形和接收滤波器联合优化设计涉及发射波形和优化和接收滤波器的优化。其中,接收滤波器约束条件简单,最优接收滤波器很容易获得,联合设计的关键是发射波形的优化,不同波形约束条件下的求解方法也不尽相同。文献[56]将机载MIMO-STAP波形优化问题转化为二次波形优化问题,并采用MM技术寻找优化问题目标函数的紧致下界,在此基础上设计了能量约束、恒模约束以及恒模和相似性约束下的联合设计方法。结果表明,这3种方法不仅收敛速度快,而且能够有效提升输出SCNR性能。文献[57]和文献[58]首次将黎曼几何优化方法引入到机载MIMO雷达发射波形和接收滤波器联合设计中,通过黎曼流形来解决恒模约束下的联合设计问题,该流形优化方法将约束优化问题视为一个约束搜索空间上的无约束优化问题,并提出黎曼梯度下降算法和黎曼信任域算法来进行求解。结果表明,该方法能够在每次迭代时同时更新发射波形和接收滤波器,且计算量远小于基于SDP的优化方法。此外,该方法可以推广到解决复杂波形约束和目标函数情况下的联合设计问题。

图8(a)和图8(b)给出了文献[56]算法1和文献[55]算法1的输出SINR随目标归一化多普勒频率变化和计算时间变化的情况。从图8(a)可看出,文献[56]算法1和文献[55]算法1具有几乎相同的输出SINR,且均优于正交波形和相干LFM波形。从图8(b)可以看出,文献[56]算法2的计算量明显小于其他对比算法。图9(a)和图9(b)给出了文献[58]中不同算法的输出SINR随目标归一化多普勒频率和计算时间的变化情况,文献[58]提出的黎曼流行-最速下降和黎曼流行-共轭梯度属于黎曼一阶算法,黎曼流行-信赖域属于黎曼二阶算法。可以看出,黎曼流行-最速下降、黎曼流行-共轭梯度和黎曼流行-信赖域得到的输出SINR性能均优于文献[55]算法,而且前3种算法的收敛速度远快于文献[55]算法。

图8 不同算法的输出SINR和计算时间对比Fig.8 Comparison of output SINR and computation time of different algorithms

图9 不同算法的输出SINR和计算时间对比Fig.9 Comparison of output SINR and computation time of different algorithms

2016年,文献[59]研究了STAP中的波形优化问题,其中假定杂波响应与发射波形是相关的,由于权矢量和波形向量的目标函数是联合非凸的,而单个权矢量和波形的目标函数是凸的,采用约束选择最小化技术在保持一个矢量不变的同时迭代优化另外一个矢量。在此基础上,文献[60]研究了信号相关STAP下联合信号-波束形成器的优化问题,并提出一种松弛双二次优化方法来寻找可行的解。此外,还将关于波形的能量约束推广到了恒模约束和相似性约束[61]。

然而,上述方法设计出的波形相位是连续的,很难在实际雷达中获得应用。为此,Tang等[62]在MIMO-STAP发射波形和接收滤波器联合设计中考虑了波形的恒模约束和有限相位约束

(9)

图10 不同算法的输出SINR随归一化多普勒频率的变化Fig.10 Output SINR of different algorithms versus the normalized Doppler frequency

为实现与通信系统的共存,童日武等[64]研究了PAPR约束下机载MIMO雷达与通信频谱共存的联合设计

(10)

2.2 先验条件非理想时机载雷达稳健波形优化设计

当前关于先验条件理想时的机载雷达波形优化设计考虑的主要是机载MIMO雷达体制,因此,下面从机载MIMO雷达稳健发射波形优化设计、机载MIMO雷达发射波形和接收滤波器稳健的联合优化设计两个方面进行总结。

2.2.1 机载MIMO雷达稳健发射波形优化设计

针对空时导向矢量误差存在时MIMO-STAP的波形优化问题,文献[65]将目标空时导向矢量建模为

(11)

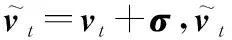
(12)

文献[66]是一个极大化极小优化问题,采用对角加载技术将原问题转化为一个SDP问题进行求解。但目标导向矢量的松弛约束和对角加载技术得到的波形协方差矩阵仍是次优的。为此,Tang等[48]采用更普遍的不确定集来描述导向矢量误差,然后精确推导出使SINR最小的最差目标导向矢量,并舍弃启发式对角加载方法,来寻找全局最优的且对目标导向矢量误差稳健的波形协方差矩阵。图11给出了文献[48]中最差输出SINR随不确定集大小ε的变化。

图11 最差输出SINR随不确定集大小的变化Fig.11 Worst-case output SINR versus the size of the uncertain gather

由图11可以看出,所有方法的最差输出SINR随不确定集大小的增加而下降,而文献[48]的方法优于其他3种方法。

进一步地,文献[66]研究了杂波先验信息不准确时MIMO-STAP波形优化问题:

(13)

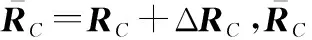
2.2.2 机载MIMO雷达发射波形和接收滤波器稳健的联合优化设计

部分学者针对先验信息不准确条件下机载MIMO雷达发射波形和接收滤波器的联合设计进行研究。文献[71]针对机载MIMO雷达目标导向矢量不准确导致性能下降的问题,建立了目标导向矢量的椭球不确定集,以最大化不确定集上的最差输出SINR作为优化准则,考虑波形的能量约束和PAPR约束,建立了发射波形和接收滤波器稳健联合设计问题模型,但所提的求解方法计算复杂度较高。

童日武等[72]针对目标先验信息未知情形,设计了一组与目标参数不确定集对应的线性接收滤波器,以最大化最差情况下的输出SINR作为优化准则,同时考虑了波形的能量约束、相似性约束和PAPR约束

(14)

采用类似文献[64]中的方法求解文献[73]中的问题,并利用可行点追踪连续凸近似算法求解最优波形。计算结果表明,该方法对目标先验信息的失配具有稳健性。

文献[73]针对目标多普勒频率和空间锥角的不确定性问题,研究了MIMO-STAP雷达慢时间稳健发射接收联合优化设计,设计了平均输出SCNR,作为联合优化设计目标函数:

(15)

(16)

式中:s∈S表示波形的恒模约束或相似性约束。文献[73]提出了4种迭代优化算法进行求解。其中,算1和算法3基于SDP和随机化,或者秩一分解方法,算法2和算法4是基于分式规划和拟幂法。图12给出了文献[73]中算法2和算法4在确定性和随机性场景下的空时响应图。由图12可以看出,两种算法空时响应图的主瓣在目标参数不确定情形下要比目标参数确定性情形下略大,这意味着两种算法在目标参数不确定时具有更好的稳健性。图13给出了输出SCNR随目标参数不确定性的变化。由图13可以看出,整体上,不同算法的输出SCNR随着参数不确定性的增加而下降,这是以增加系统的稳健性为代价的。

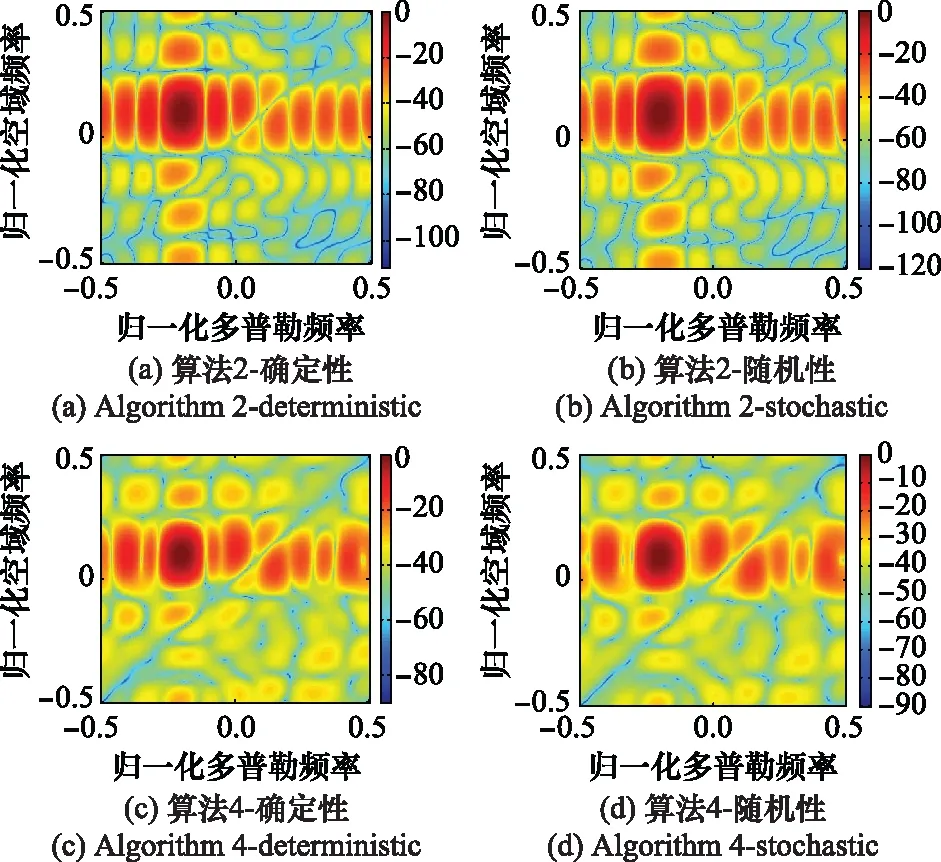
图12 目标参数确定和不确定下算法2和算法4的空时响应图Fig.12 Spatial-temporal beampattern of Algorithm 2 and Algorithm 4 under the target parameter deterministic and stochastic cases

图13 输出SCNR随目标参数不确定性的变化Fig.13 Output SCNR versus the target uncertainty value

3 新体制机载雷达波形优化设计研究展望

新体制机载雷达具备数字化、多功能、战场环境感知、低截获和阵元效率高等现代雷达发展的综合特性,能够有效适应未来预警机小平台、多功能、一体化的设计需求,能够有效适应未来雷达反隐身、抗反辐射导弹、抗复杂干扰作战的军事需求。因此,新体制机载雷达是未来机载雷达发展的重要趋势,新体制机载雷达的发展也必然引发信号处理领域新理论和新技术的发展。其中,新体制机载雷达波形优化设计是雷达应对复杂电子对抗环境的关键技术,国内外学者从先验条件理想与否、阵列收发结构、不同任务和约束条件等方面出发,提出了丰富的机载雷达波形优化设计方法。随着战场电磁环境的日趋复杂,抗动态杂波和抗复杂干扰的难度也在不断增大,现有的研究仍存在很多不足,需要进一步开展深入研究。

(1) 非理想条件下机载雷达波形优化设计

现有的研究大多针对目标、杂波和干扰等先验条件理想时进行波形优化设计和目标检测[46-64]。部分文献研究了非理想条件下的机载MIMO雷达波形优化设计[65-74],但这些研究成果仍然不足以支撑机载雷达适应实际复杂多变的工作环境。这是由于实际机载雷达面临的战场环境瞬息万变:一是目标参数变幻莫测,机载雷达面临的探测目标正在向“高空、高速、高机动”和“低空、低速、低散射”方向发展,导致目标参数变化多端,很难获取准确的目标先验信息;二是杂波非平稳、高动态起伏等问题。现代战争中机载雷达需要在城市、山区、森林、草原、海洋以及海陆交界等各种地形环境下执行任务,当杂波环境动态多变时,传统的杂波模型将与实际杂波场景失配[9];三是电磁干扰环境复杂多变,机载雷达面临着来自陆地、海洋和空中等各方面的干扰,干扰的样式越来越多,干扰的强度越来越大。因此,建立与实际目标、杂波和干扰相适应的信号模型,并建立相应的不确定模型,开展非理想条件下机载雷达波形优化设计,提升机载雷达对实际工作环境的适应性具有重要的军事意义。

(2) 新体制机载雷达波形优化设计

现有的研究主要以机载相控阵体制和机载MIMO体制着手,从空域和时域(慢时间、快时间)的角度开展波形优化设计来抗杂波和干扰。然而,在动态时变的杂波环境和复杂多变的干扰环境下,仅从空时域开展机载雷达波形优化设计,无法有效对抗各种杂波和干扰。以频率分集阵列、空时编码阵列为代表的波形分集阵列雷达通过阵元间发射波形的变化,形成目标和干扰之间的多维参数差异,从而使系统具有更多可用的距离维自由度,在抗距离模糊杂波[75-80]和主瓣欺骗干扰上具有很大的优势[81]。机载极化雷达充分利用空域、时域和极化域的信息进行极化空时联合处理,增强了强杂波背景和干扰下的慢速目标检测能力[82]。因此,基于频率分集阵列、空时编码阵列以及极化阵列,充分利用空域、时域、频域和极化域信息,开展机载波形优化设计,具有重要的应用前景。

(3) 基于频谱感知的机载雷达波形优化设计

随着战场信息化程度的不断加深,各种类型的电子装备不断涌现,高速发展的电子装备对电磁频谱的需求越来越多,使得电子装备不断地与机载雷达争夺频谱资源。随着无线设备数量的爆发式增长和对高数据传输要求更高的带宽需求的增加,有限的电磁频谱越来越拥挤[13-14]。日益拥挤的频谱环境使得机载雷达与各种电子设备的工作频段不可避免地出现重叠,导致两个系统之间产生相互的电磁干扰;此外,作为信息化作战的体系核心,机载雷达除完成目标探测任务,还担负着侦察情报、指挥控制、信息对抗和综合保障等任务,促使机载雷达向多功能一体化方向发展。因此,频谱感知是下一代机载雷达必不可少的技术,实现频谱共存不仅对机载雷达波形提出了更高的要求,也对如何在有限的频谱资源中进行机载雷达运动目标检测提出了更高的要求,亟需开展基于频谱感知的机载雷达波形设计[83-88]。

(4) 基于稀疏恢复的机载雷达波形优化设计

压缩感知及稀疏重构理论为机载雷达信号处理提供了新的研究思路。近十年来,基于稀疏恢复的STAP技术受到了学者的广泛关注,该技术的主要思想是利用杂波功率谱在角度-多普勒平面上的稀疏性,采用稀疏恢复算法实现杂波空时功率谱的高分辨估计,该技术对于提升小样本条件下的杂波抑制性能具有先天优势[89-92]。 然而,现有的基于稀疏恢复的STAP技术大都针对雷达发射固定的波形,难以根据实际工作环境实现发射波形的动态优化设计。将发射波形与后端的稀疏重构算法的设计联合起来,构建发射波形-重构算法-发射波形的闭环反馈机制[93],开展基于稀疏恢复的机载雷达波形优化设计,对解决非均匀环境下样本不足问题具有重要意义。

4 结束语

机载雷达作为预警机的核心,正面临着高动态杂波环境和复杂电磁对抗环境的挑战,迫切需要发展新体制机载雷达及相应的波形优化技术。本文在给出认知雷达基本原理和新体制机载雷达波形优化设计的概述后,从先验条件是否理想的角度对机载雷达波形优化设计的研究现状进行了总结和归纳,针对现有研究的不足,对新体制机载雷达波形优化设计未来的发展趋势进行了探讨。本文既是对当前机载雷达波形优化设计技术的阶段性总结,也包含对该领域未来发展趋势的合理预判,该领域的研究对未来机载认知雷达系统的发展提供了理论支撑。