基于CUDA 加速的GPS L1C/A 实时信号发生器设计*

王子涵，巴晓辉，2，3，姜 维，2，3，蔡伯根，王 剑，2，3，文 韬，2，3，郭 旗

（1.北京交通大学 电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.北京市电磁兼容与卫星导航工程技术研究中心，北京 100044；4.北京交通大学 计算机与信息技术学院，北京 100044）

0 引言

进入21 世纪后，随着人类步入到信息数字化时代，全球导航卫星系统GNSS（Global Navigation Satellite System）的应用也从最初的军事领域，渗透到包括交通、金融、航空、航海、测绘等生活的方方面面，成为关系人们日常生活的一项重要基础设施[1]。

全球卫星导航系统一般由地面控制部分、空间卫星星座和地面用户设备三部分组成。除了要保证太空中卫星的正常工作外，地面上的用户设备也是系统正常运行的关键一环，而各种高性能接收机的开发与调试都离不开信号模拟器[2]。与直接让接收机接收真实卫星信号或使用信号回放仪回放卫星信号的方法相比，信号模拟器可以根据用户的需要，设计不同环境、不同复杂场景下的模拟卫星信号，从而为导航接收机等设备提供仿真测试条件[3]。此外,卫星导航系统在军事领域的更多潜力也在被迅速开发，通过使用欺骗技术，使得敌方的精确武器、设备失去作战能力，具有非常高的军事研究价值，并已成为世界各国研究的热点。而产生实时高效的模拟卫星信号则是研究欺骗与反欺骗技术的技术前提，具有重要意义[4,5]。

传统的GNSS 信号模拟器由仿真控制软件（simula‐tion control software）和信号生成硬件（signal generation hardware）组成[6-7]。仿真控制软件可以通过设置载体运动轨迹和模拟场景来生成GNSS 信号。在信号生成硬件中，数字信号处理（Digital Signal Processor,DSP）芯片负责计算导航信息、状态参数、控制参数。通过现场可编程门阵列（Field-Programmable Gate Array,FPGA）实现信号编码和直接序列扩频调制，生成数字中频信号。最后，再经过模数转换器（Digital to Analog Converter,DAC）和数字中频信号的上变频得到所需的卫星信号[8-9]。

传统的信号模拟器通常采用“FPGA+DSP”结构。这种系统需要定制化，硬件成本高且灵活性低，用户不能方便地更改导航电文、扩频码等信息。此外，对于传统信号模拟器，诸如认证信息添加和多径效应模拟等功能的拓展也比较复杂。而模拟器在实际运用过程中经常需要根据需要，对不同场景、各种状态的卫星信号灵活模拟，传统信号模拟器亟需改进。

为解决上述问题，基于软件无线电（Software De‐fined Radio,SDR）的GNSS 模拟器体系结构开始被人们所采用[10]。基于软件无线电的GNSS 模拟器使用仿真软件来代替DSP 和FPGA 生成数字中频信号，由于整个中频信号的产生是由软件端完成的，因此系统功能的变更和拓展较为方便。此外，在多通道、高采样率的情况下，普通的CPU 很难做到实时地生成模拟GNSS 信号。因此，通过运用GPU 加速的方法来满足实时、多通道、高速率GNSS 信号的模拟需求成为很多人的选择[11-12]。

针对基于GPU 的卫星生成信号算法，前人已经进行了一些研究。文献[13]对GPU 优化加速的方法进行了系统性的总结，并通过在相同条件下比较使用CPU 和CPU+GPU 两种方法产生卫星信号的快慢，证明了GPU对于信号加速的可行性及有效性；文献[14]针对GPS L1信号，对程序的并行线程结构、内存分配方式进行了优化，实现了多通道高采样率的卫星信号的实时生成；文献[15]设计了一种数据结构，以提高GPU 访问伪码数据的速度，并最终高速实时生成了BDS B1I 信号。但是，前人关于GPU 信号加速的研究，主要是针对并行程序部分的线程结构、内存访问方式以及数据存储方法的优化，而系统在执行核函数以外的命令时，仍然是以串行运行为主的方式，这造成了资源上的浪费。对此，本文在继承前人优化思想的基础上，运用异步运行的思想，引入了CUDA 流的概念，对GPU 产生卫星信号的过程进行进一步的加速。

在本文中，提出了一种SDR GNSS 信号模拟器的体系结构。在这个结构中，仿真控制软件基于本文提出的优化算法高速实时产生GNSS 数字中频信号，然后通过高速接口将信号送到USRP 中，再经过正交矫正、数模变换、上变频，最后通过射频端输出，生成模拟GNSS 信号。由于中频信号的产生是在软件中进行的，因此整个系统具有良好的可拓展性，便于测试与验证。

1 GNSS 模拟器体系结构

1.1 系统总体结构

SDR GNSS 模拟器由软件端和硬件端两部分组成，如图1 所示。数字中频信号由仿真控制软件控制GPU实时产生。软件端实时为用户计算可见卫星的参数（包括载波相位、伪码相位、信号幅度），并产生对应时间段的数字中频信号。然后，该信号经过高速数据传输接口实时传输至硬件端，硬件端对中频信号进行一系列处理后通过射频前端发射，生成模拟GNSS 信号。

图1 GNSS 信号模拟器体系结构

1.2 GNSS 中频信号模拟

GNSS 数字中频信号指的是接收机接收到的卫星信号在经过下变频、模数转换后得到的数字信号。本文采用中频调制方案，即先在上位机中生成中频信号，再将信号经由USRP 调制到射频频段。单颗卫星信号参数包括信号幅值、导航电文、扩频码相位、载波相位（不同的GNSS 系统的卫星信号格式有所差异，本文以GPS L1C/A 信号为例），信号采用BPSK（Binary Phase Shift Keying，二进制相移键控）进行调制，卫星的中频信号[16]可以表示为：

其中，n(tR)表示接收机tR时刻收到的高斯噪声，Ai表示第i颗卫星的幅值，ti,S表示第i颗卫星在接收时刻tR对应的发射时间，Di(ti,S)和Ci(ti,S)分别表示卫星在ti,S时刻的导航电文和扩频码，fc表示中频，fi,d表示第i颗卫星的载波多普勒频移。

GNSS 模拟器生成数字中频信号的方法是每次生成T时间（仿真步长）的数据。也就是说，假设采样率为FS，则每个模拟步骤中生成的GNSS 采样点的数量为N=FS×T。即为保证信号的实时生成，SDR GNSS 模拟器必须保证能在T时间内至少产生N个采样数据。

由式(1)中可知中频信号的基本构成，其中卫星信号的导航电文、扩频码都可以根据GPS 的ICD 文件获取，故生成模拟信号的关键在于确定卫星信号的伪码相位和载波相位。本文通过一阶线性插值的方法来得到仿真步长T内的伪码和载波相位。生成采样数据的过程如下：

(1)假设L是被分配通道的卫星的数量。首先，L不应大于设置的可模拟的最大通道数。

(2)记通道i卫星信号的第k个采样点的伪码相位和载波相位分别为ϕi[k]和θi[k]，其值可由以下公式给出：

其中ϕFi和θFi分别表示初始的码相位和载波相位，ϕSi和θSi表示码相位和载波相位每个采样点之间的增长量（伪码和载波的步进）。

(3)由上述过程可以得到任一通道任一采样点的码相位和载波相位序列，并由此可以产生任意单通道的信号，然后再与信号功率与伪码序列的幅度参数进行调制。对于采用BPSK 调制的GPS L1 信号而言，生成的单通道信号可以表示为：

其中，ψi[k]表示第k个采样点的导航电文比特数，可以由码相位得到；表示i通道下第k个采样点I 路和Q 路的输出值。

(4)对L个通道的I 路和Q 路信号分别求和：

确定初始伪码和载波相位的步骤如下：

(1)确定初始载波相位。卫星与用户之间的距离除以射频信号的波长，并去掉结果的整数部分，从而得到信号的初始载波相位（单位为2π）。

(2)确定初始码相位。GPS L1C/A 码的频率为1.023 MHz，且C/A 码一共有1 023 个码片，故发送一个完整的C/A 码码片的时间为1 ms，所以初始码相位就等于当前时间的毫秒数的小数部分再乘以C/A 码的码片数。

确定伪码和载波相位步进的步骤如下：

(1)确定多普勒频移。在理想情况下，每一个采样点的多普勒频移都可能不同，但在实际情况中，由于受到计算机算力和内存的限制，不可能做到实时计算每一个采样点的多普勒频移。在这里认为在一个很短的时间dt（比如0.1 s）内，信号的多普勒频移是相等的。那么就可以先根据两个相邻时刻的伪距求出径向速度，再求出多普勒频移。

其中v表示所求的径向速度；r1和r0表示两个相邻时刻的伪距；dt表示两伪距的时间差，同时也是仿真步长；fd表示所求的多普勒频移；λL1为GPS L1 信号的波长。

(2)确定伪码和载波的步进。计算步进的计算方法是由信号频率来除以采样率，得到的就是每两个采样点之间相位的增长量。具体方法如式(9)、式(10)所示：

其中θSi和ϕSi为所求的载波和伪码步进；fc为中频载波频率；FS为采样率；fcode为扩频码的频率，这里为1.023 MHz；M为扩频码频率与射频信号频率的比值，这里为1/1540。

2 GPU 算法优化

2.1 并行计算软件架构

为了提高GPU 的资源利用率，本文通过划分计算任务和内存使用来优化CUDA 程序。每个采样点的模拟数字中频信号的生成过程如图2 所示。

中频信号产生及传输的过程如下：首先，用户对场景参数进行设置。然后，CPU 获取到用户设置的参数，并由此生成包括扩频码、导航电文、初始码相位、初始载波相位及其步进等信息。接着将扩频码、导航电文连同本地产生的正弦表、余弦表一同送入GPU 的纹理内存中，将初始码相位和载波相位及其步进送入每个线程中，每个线程的计算结果通过共享内存将数据合并输出，再由页锁定内存传回到CPU，再将结果提供给射频端。

式（7）、式（8）中提到，多普勒频移在dt时间内是保持不变的。即在dt的时间内，采样点具有相同的载波和码相位步进，由此可以得到本文的并行计算模型，如图3所示。

图3 并行计算模型

K、M、N分别表示单个block 中线程的行数和列数以及所使用的线程块的个数。它们应满足下列关系：

GPU 算法的优化包括内存优化、并行优化、CUDA流加速3 部分，下面分别进行介绍。

2.2 内存优化

GPU 的内存种类有寄存器、共享内存、纹理内存、常量内存和全局内存。不同内存之间的访问延迟差别很大。由于GPU 上有足够多的ALU（算术逻辑单元 Arith‐metic and Logic Unit），因此程序算力的高低主要受访问速度的影响，表1 为部分GPU 的内存带宽大小。在信号生成的过程中，会涉及大量的CPU 和GPU 的数据传输，故GPU 内存的合理使用可以有效提高计算效率。

表1 GPU 各种内存带宽

(1)寄存器。每当核函数声明一个变量，系统就会自动为所有要执行该核函数的线程分配含有这个变量的寄存器，不同寄存器之间的数据不能互相读取。

(2)本地内存。当核函数调用了过多的变量导致寄存器溢出时，数据会被存放到本地内存中。本地内存为各个线程私有，不能互相访问，性能上与全局内存相同。

(3)共享内存。共享内存的数据为同一个block 中所有的线程所共享，并具有较快的访问速度。

(4)纹理内存。纹理内存是所有线程都可以进行访问的只读空间，且由于其访问的读取可以通过纹理缓存进行加速，故其访问的速度高于全局内存。

(5)全局内存。全局内存无论是CPU 还是GPU 都可以进行访问，其特点是速度较慢但是容量较大。

在CUDA 编程中，如果使用了带宽较小的存储器，会大幅降低程序的运行速度。灵活选择内存访问方式以匹配不同的数据，避免计算过程中的数据等待，是提高算法性能的重要方式。本文主要采用共享内存和纹理内存来提升程序运行效率。

2.3 线程架构并行优化

对线程的并行优化主要考虑以下两个方面：

(1)确保使用了足够多的warps（线程束），以确保SM（Streaming Multiprocessor）没有进入空闲。SM 也叫GPU 大核，可以看作GPU 的心脏（对比CPU 核心）。CUDA 将这些资源分配给所有驻留在SM 中的threads。warp 是GPU 并行计算的基本单元，一个warp 包含32 个并行线程，这32 个线程同时执行同一条指令，一个warp中的线程必须在同一个block 中。一个SM 中，并不一定会一次性执行完warp 中的所有内容（例如经常需要等待CPU 向其传输数据），这个时候就切换到别的warp 进行计算，由此可以避免等待的时间，所以理论上来说，当一个SM 中有足够多的warp 进行切换时，就可以避免因为SM 等待而造成的时间浪费。

(2)基本上warp 分组的行为是由SM 自行进行的，SM 会以连续的方式来进行分组，且最后不足32 的部分独立组成一个warp，而这会导致线程算力的浪费。所以应尽量确保block 中使用的线程数量为32 或16 的整数倍，以节约计算机的运行资源。在实际情况中，K的值会随着分配卫星通道数的需要而进行改变，故在本文设计中M为32 或16 的整数倍。

2.4 CUDA 流加速

CUDA 流在加速程序方面具有着重要的作用。CUDA 流表示一个GPU 的操作队列，并且该队列中的操作将以指定的顺序执行。队列中由一个或多个引擎执行内存复制操作，以及一个引擎来执行核函数的调用。这些引擎彼此独立地对操作进行排队，如图4 所示。

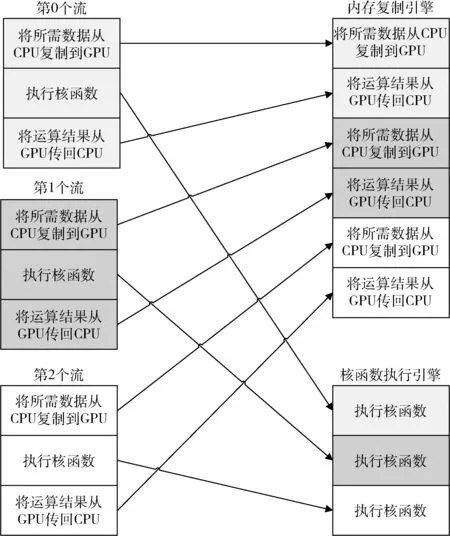
图4 理想情况下CUDA 流的工作过程

然而，在实际情况下，由于程序存在着严格的依赖关系（即在同一个流中，必须在执行完核函数后，才能将数据从GPU 传输回CPU），这就要求安排合理的队列顺序，减少程序等待的时间。也就是说，如果同时调度某个流的所有操作，那么由于程序的依赖关系，很容易会在无意中堵塞另一个流的内存复制操作或核函数调用操作，为解决这一问题，将操作放入流的队列时，应采用宽度优先的方式，而非深度优先方式。假设内存复制时间与核函数运行的时间大致相当，那么程序的执行时间线如图5 所示。

图5 程序执行时间线

由于采取了宽度优先方式将操作放入各个流的队列中，因此第0 个流执行核函数的操作将不会阻塞第一个流对a 和b 的内存复制操作。这使得GPU 能够并行地执行复制操作和核函数，从而使得应用程序的运行速度获得显著提升。

3 信号测试与验证

3.1 信号测试与验证流程

信号发射与验证的流程如图6 所示，首先用户对移动轨迹、广播星历、仿真时间、模拟步长、信号通道数等输入参数进行配置，并将其传入到计算机中。然后CPU对输入参数进行读取、处理，将产生数据所需的参数传入GPU，GPU 通过并行运算快速生成中频信号，并将结果传回CPU，通过射频端（USRP）发送，由硬件接收机验证信号的正确性。

图6 信号测试流程

对射频前端发出信号进行频域分析，结果如图7 所示。结果表明模拟器生成信号的频谱特性与真实信号的频谱特性相一致。

图7 中频信号频谱特性

通过将射频端的信号连接到Ublox 接收机中进行分析解算，验证信号的正确性，结果如图8 所示。

图8 硬件接收机验证信号正确性

3.2 加速效果验证

本文通过运用GPU 加速算法来实现卫星数字中频信号的高效实时生成。开发平台是计算机统一设备架构（CUDA）下的C 编程。本文所采用的GPU 型号及其具体参数如表2 所示。

表2 硬件型号及性能参数

本小节针对2.2、2.3、2.4 小节所提出的优化方法进行实验验证。图9 是在固定可见卫星为10 颗的情况下，不同采样率下生成1 s 中频信号所花费的时间。

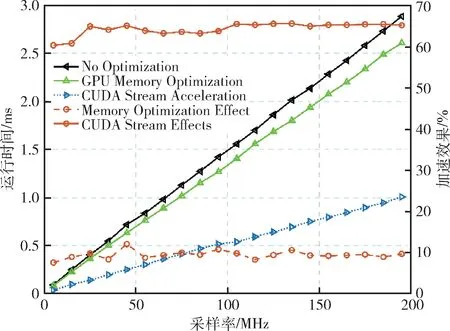
图9 不同采样率下的加速效果

从图9 可以看出，不同信号采样率下，采用内存优化方法加速程序后，程序运行速度相比优化前提升了约10%；采样CUDA 流+内存优化方法加速程序后，程序运行速度相比优化前提升了65%，加速效果明显。

图10 是针对2.3 小节提到的线程架构优化方法进行验证，控制可见星数量固定为10 颗，改变每个线程块中线程的列数（即2.1 小节中M的值），统计10 MHz 采样率下生成1 s 中频信号所用的时间。

图10 线程架构对运行时间的影响

从图10 可以看出，当M为16 或32 时，程序运行速度相比其他情况更快，这是因为在可见星数量为10 时，只有当M取值为16 的倍数时，单个线程块内线程的数量才能是32 的倍数，使得每一个线程束都能高效率工作。

3.3 与其他加速效果的比较

在文献[16]中，只是将使用GPU 产生数据的时间与单纯使用CPU 的时间进行了对比，并没有针对GPU 的算法进行进一步的优化，其产生1 min 的GPS 信号（5.72 MHz 采样率）所花费的时间为58.66 s，相比本文的运行时间可以充分体现本文针对GPU 优化的效果；与文献[15]的结果相比较，在50 MHz 采样率情况下，产生1 s 的B1I 信号所花费的时间为304 ms，作为对比，本文采用的方法产生1 s 信号所用时间为271.255 ms，考虑到文献[15]所采用的GPU 为专业级GPU:Quaro M5000，与本文中所使用的GTX 1050Ti 相比性能优势明显，可以认为本文所采用的加速方法与之相比有明显改进。

4 结论

本文提出了一种基于GPU 加速的GNSS 模拟器信号生成方法。本文采用“CPU+GPU”异构运算架构，实现了GPS L1C/A 码中频信号的实时生成，并通过USRP播发。通过这种方式，本文实现了对真实卫星信号在地面情景下的精准实时复现，通过软件仿真和硬件接收机接收验证了信号的正确性。此外，本文还通过优化GPU内存、设计线程并行结构、运用CUDA 流加速的方式使得数字中频信号的生成更加高效快速。经过测试，在RTX1050TI 设备上，可以在信号采样率195 MHz，10 颗可见卫星情况下，实现卫星信号的实时生成。本文所涉及的代码已在GitHub 上开源[17]。