倒立式三视场施密特望远镜关键技术研究

赖新华，李金鹏，彭润富，杨永兴，王鑫蕊，石旺舟

（1.上海市星系与宇宙学半解析研究重点实验室，上海 200234；2.上海师范大学 数理学院，上海 200234；3.中国科学院南京天文仪器有限公司，江苏 南京 210042；4.中国科学技术大学 南京天文仪器研制中心，江苏 南京 210042）

引言

施密特望远镜在天文观测等领域具有广泛应用，因此国内外学者对施密特望远镜的关键技术进行了深入研究。李德培将云南天文台的施密特望远镜改装成水平结构，用于观测人造卫星及空间碎片[1]。EGLITIS I 研究了直角坐标测定和测光方法，对巴尔顿天文台的施密特望远镜扫描仪进行了精度评估[2]。俞金梅将一种缩焦器应用在一台施密特卡塞格林式望远镜上，缩短了焦距，从而可以使用CCD 相机来代替照相底片[3]。周志中采用2 台步进电机取代复杂驱动系统，改进了北京天文台的施密特望远镜，实现了计算机控制[4]。WILLSTROP R V 研究了具有3 个反射面的Mersenne-Schmidt 望远镜，采用了更为紧凑的设计，使得该望远镜有更大的相对口径和视场[5]。左恒等人为装卸LAMOST 的子镜专门设计了大型自动机械装卸装置，实现了大跨度、高精度自动定位，在望远镜的维护中发挥了重要的作用[6]。董云芬等人推导了斜入射反射式施密特校正板方程，利用补偿器和干涉仪实现了面形的高精度检测，拓展了施密特望远镜在大视场、宽波段天文观测方面的研究[7]。雷存栋等人设计了离轴全反式施密特光学系统，可应用于宽波段、高分辨率紫外成像系统[8]。HRABOVSKY M 研究了有、无施密特校正板情况下的施密特望远镜系统，分析了具有1m Rad 缺陷的系统三维能量分布[9]。蒋兆基等人在北京天文台采用Thomson CCD 进行BVRI四色测光，论证了BAO-CCD 系统在施密特望远镜上测光的可行性[10]。

以上对施密特望远镜的研究，工作方式大多是指向不同天顶角进行观测，直接获取天体信息。随着航天领域需求不断扩大，施密特望远镜的应用得以扩展。例如，倒立式施密特系统的提出，为同时观测多天区天体、测量自身空间姿态信息提供了一种新的思路。借助于倒立式施密特望远镜特有的大视场、多天区观测优势，可以不断提高搭载平台的空间姿态测量精度，扩大其应用范围。例如，DANIELE M 提出了一种三视场Schmidt-Cassegrain 结构星敏感器，能够实现对3 个天区同时观测，从而反演出搭载平台的空间姿态信息[11]。WU Feng 对多个视场（FOV）的姿态计算方法进行了研究，为附近的飞行器可提供准确的导航信息[12]。JOZEF C 使用地球传感器数据确定旋转轴姿态技术，用于航天器姿态的控制[13]。还有学者聚焦于多视场星敏感器的工作模式，提升卫星的空间姿态测量精度[14-16]。

虽然倒立式三视场施密特望远镜已经有相应的科研成果，但更多关注的是在应用方面，对于其本身的关键技术研究较少。针对基于三分区镜的倒立式三视场施密特望远镜系统，本文研究了其中的关键技术。采用数学几何模型分解方法，对实现多天区观测功能的三分区镜设计方法进行了讨论；使用有限元法分析主镜重力形变，剖析其对光学系统像质的影响；利用光学设计软件对施密特修正镜加工误差进行仿真，进而探讨对像质的影响程度；应用蒙特卡罗法，研究了该系统的杂散光；最后，对望远镜光学系统进行了实验检测，验证了该倒立式施密特望远镜能够进行高精度成像。

1 基本原理

1.1 倒立式三视场施密特望远镜系统

本文研究的倒立式三视场施密特望远镜光路如图1 所示。主镜为口径300 mm 的球面镜，光学系统总长约为1 920 mm，3 个视场的视轴夹角互为90°。三条主光线同时从空间中不同视场入射，由三分区镜反射后互相平行。该平行光经过施密特修正镜组，再由主次镜反射聚焦于卡塞格林焦面上。最后在卡塞格林焦面上安装探测相机，由相机采集得到3 个视场方向的叠加星图。

图1 倒立式三视场施密特望远镜光路图Fig.1 Diagram of light path of inverted 3-FOV Schmidt telescope

1.2 三分区镜设计方法

三分区镜是该望远镜系统的重要组成部件，为了实现三视场观测，需要对其进行研究和设计。三分区镜光学理论模型如图2 所示。图2 中3 条主光线同时入射三分区镜，分别交于A、B、C点，且延长线交于O点，反射后平行进入光学系统。连接点O、A、B、C，建立三分区镜光反射数学模型，如图3(a)所示。图3 中箭头指示光线行进方向。

图2 三分区镜数学模型提取Fig.2 Mathematical model extraction of 3-facet mirror

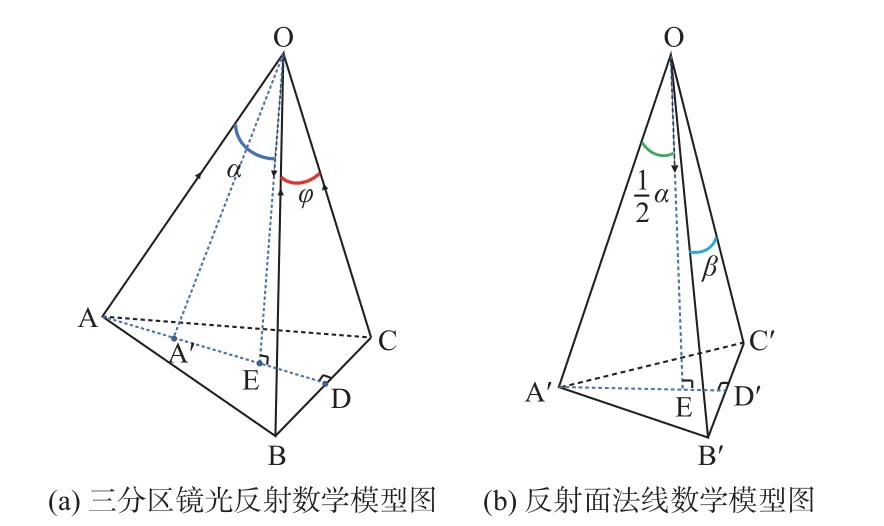
图3 三分区镜模型分解Fig.3 Model decomposition

由3 条光轴的对称性可知，该数学模型为正三棱 锥。设入射 光之间 夹角为 φ，OE 为高，OA′为∠AOE 的角平分线，∠AOE=α。由反射定律可知，OA′为反射面 1 的法线。则有：

在 ∆OBC中，有：

由（1）式、（2）式可得到 α与φ之间的关系式为

类似地，作出 角平分线 OB′、OC′，连接点 A′、B′和 C′，得到由法线组成的新正三棱锥，如图3 (b)所示。在新三棱锥中，令∠B′OC′=β（即三分区镜3 个平面间的夹角），同理有：

将（3）式代入（4）式，可得：

（5）式即是三视场视轴夹角与分区镜面夹角之间的代数关系式。

2 倒立式三视场施密特望远镜关键技术研究

2.1 主镜重力形变分析

望远镜主镜加工时镜面朝上，实际使用时镜面朝下，两者产生的重力形变不同，由此产生的面形差别是影响整个系统波像差的重要因素，因此，需要对主镜重力形变进行研究。主镜采用三点支撑[17-18]，材料是微晶玻璃，口径为300 mm，内径为80 mm，球面曲率半径为1 151.63 mm，边缘厚度为35 mm。使用有限元分析软件构建三维模型，如图4 (a)所示，划分的有限元分析网格如图4 (b)所示。

图4 有限元分析软件构建模型Fig.4 Finite element analysis software modeling

为求出合理的支撑半径，需要对不同支撑半径下的镜面形变进行研究。采用等间距划分方法，对不同支撑半径下镜面重力形变进行分析，最小支撑半径如图5（a）所示，最大支撑半径如图5（b）所示。所得面形RMS 随支撑半径变化如图6(a)所示。由图6（a）可知，支撑半径为95 mm 时面形改变最小，此时RMS=3.80×10-5mm。考虑到实际加工和装调，实际选取的主镜支撑半径为90 mm，在该支撑半径下，主镜面形变化呈现三角状分布，如图6(b)所示。由图6（b）可知，离支撑点越远，形变量越大，最大形变量为7.36×10-5mm。

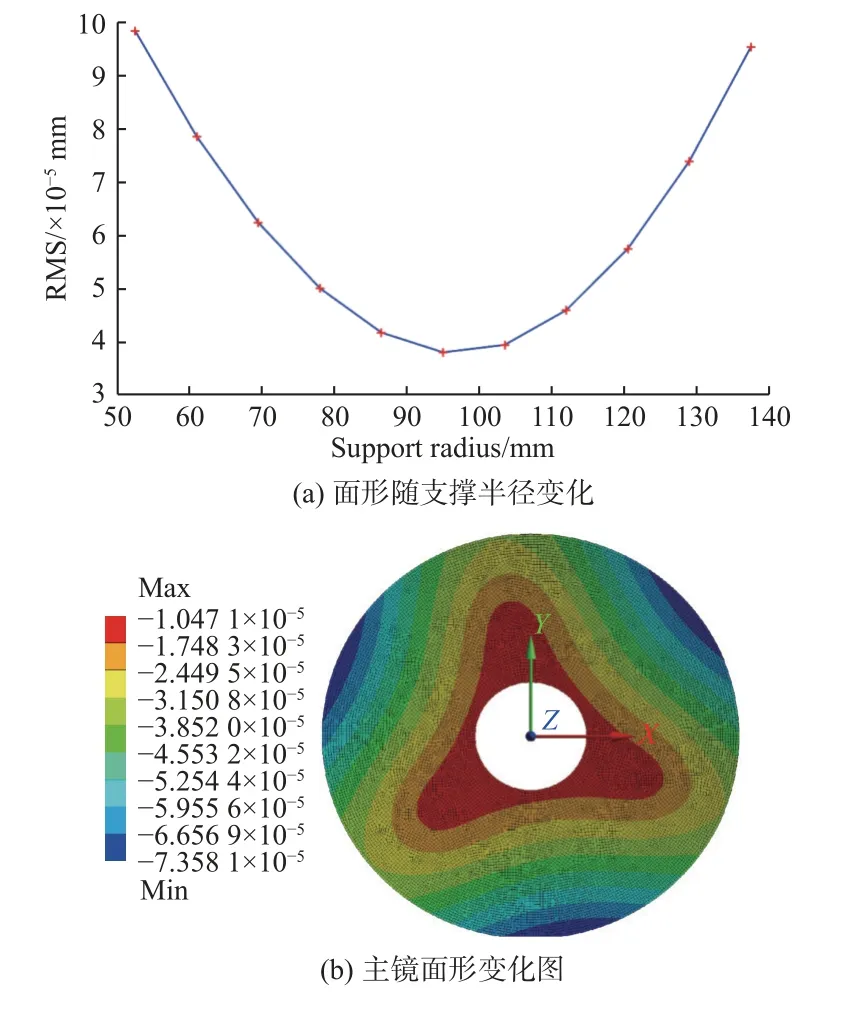
图6 支撑半径选择Fig.6 Support radius selection

将面形的重力形变数据导入MATLAB 软件，通过算法提取出前66 项Zernike 面形系数。使用光学设计软件建模，通过高斯拟合分析点扩散函数(PSF)的半高全宽(FWHM)[19]，如图7 所示，分别展示了X方向导入Zernike 系数前后的PSF。导入Zernike 系数后FWHM 由2.46 μm 退化为2.48 μm，增大了0.02 μm。同理，Y方向也求得FWHM 增大了0.02 μm。由此表明，该望远镜主镜受重力影响较小，不影响光学系统高精度成像。

图7 X 方向的PSFFig.7 PSF in X direction

2.2 施密特修正镜的加工误差分析

施密特修正镜的加工精度将影响光学系统的成像质量，因此，需要对修正镜的加工误差进行研究。使用光学设计软件建立检测光路模型，分析检测光路关键参数导致的修正镜加工偏差，得到修正镜的误差范围。将修正镜的误差导入望远镜光学系统中，分析得到其对望远镜像质的影响。

施密特修正镜检测光路如图8 所示。干涉仪到补偿镜前表面的距离为l，补偿镜的厚度、前后表面的曲率半径分别为t、r1和r2，补偿镜后表面到待测修正镜前表面的距离为d，待测修正镜后表面到球面检验镜的距离为s，且球面检验镜的曲率半径为r3。检测过程中需要使用测量杆进行中心对准，测量杆自身的长度精度为0.02 mm，此时对中心的偏差达到mm 级别，可将d和s的公差变化范围设为±1 mm。镜片厚度在加工过程中通过千分表进行测量，补偿镜厚度t的公差范围为±0.02 mm。根据实际加工能力，r1、r2、r3的公差范围可达到±0.02%，修正镜非球面曲率半径R的公差可达到±0.03R/1 000。实际研制的施密特修正镜组由2 个口径相同、接近平行平板的修正镜1 和修正镜2 组成，其作用是扩大视场及补偿色差。考虑以上检测参数误差，得到修正镜4 阶和6 阶非球面系数，如表1 所示。

表1 加入检测公差后修正镜的非球面系数Table 1 Aspheric coefficients of corrector after adding tolerance

图8 施密特修正镜检测光路示意图Fig.8 Schematic diagram of detecting optical path of Schmidt corrector

考虑到以上各种检测误差，当修正镜1取R′=5.19×104mm，=-2.25×10-10，=1.42×10-17，和修正镜2取R′′=-2.55×104mm，=4.30×10-10，=2.80×10-16时，系统波像差最大，望远镜系统波像差由 0.006 7 λ 退化到 0.039 λ(λ=632.8 nm)，FWHM 由5.16 退化到5.97。通过分析施密特修正镜检测光路中镜间距、补偿镜曲率半径等参数误差，可知修正镜的加工误差不会对光学系统像质造成影响，验证了检测方法的可靠性。

2.3 杂散光分析

杂散光也会对望远镜成像质量有影响，需要对倒立式三视场施密特望远系统进行杂散光分析。本文通过TracePro 软件建模，采用蒙特卡罗法对望远镜光学系统进行光线追迹[20]，分析杂散光一次散射对像质的影响。遮光罩三维模型图如图9(a)所示。根据Harvey-Shack (ABg)散射分布模型，分别使用黑漆和镜面设定主镜、次镜和遮光镜筒等结构的双向反射分布函数（BRDF）参数。对不同离轴角度进行光线追迹，图9(b)为离轴角0°的光线追迹图。

图9 杂散光模型Fig.9 Stray light model

望远镜的点源透过率（PST）曲线如图10 所示。从图10 可以看出，随着离轴角的增大，PST 减小，离轴角在0°～1°之间时PST 下降得很缓慢；离轴角1.4°～1.5°时，PST 急剧下降，离轴角达到1.5°之后，PST 下降到10-4量级；随着轴外视场的继续增大，在2.5°～2.6°附近又有小幅度的上升，分析其原因，可能是该角度下有较多杂散光由主次镜进入到探测器像面中。图11 分别展示离轴角θ=0°、0.2°、1.8°和2.8°下像面 照度图。从图11可以看出，0°、0.2°处于视场内，主光线强度远大于杂散光，光能量集中；1.8°和2.8°都是轴外视场角，2.8°轴外视场杂散光更少，杂散光强度远远小于主光线强度。综上所述，杂散光不影响本望远镜系统的高精度成像。

图10 光学系统PST 曲线Fig.10 PST curve of optical system

图11 不同离轴角下像面照度图Fig.11 Irradiation diagrams of image plane at different off-axis angles

3 实验研究

3.1 三分区镜研制结果

实际使用的3 个视场视轴间的夹角为90°，代入式（5）可求得 β=46.92o，即三分区镜面之间的夹角为133.08°，实际口径为305.4 mm，采用微晶玻璃镀铝膜，0.45 μm～0.85 μm 波段的平均反射率大于90%。三分区镜实物和检测结果图如图12 所示，可以看出，3 个面的RMS 分别为0.022λ，0.023λ，0.011λ(λ=632.8 nm)。

图12 三分区镜实物及各面检测结果Fig.12 3-facet mirror and test results of each surface

3.2 倒立式施密特望远镜检测实验

实际研制了基于三分区镜的倒立式施密特望远镜，主镜口径为300 mm，望远镜高约1 920 mm，如图13(a)所示。使用4D 干涉仪对光学系统进行实验检测，图13(b)为检测结果的波前图，得到PV=0.614λ，RMS=0.105λ(λ=632.8 nm)。在该望远镜光学系统中，三分区镜只起到改变光传播方向的作用，且三分区镜面形较好，对望远镜成像几乎没有影响。因此，为了配合4D 干涉仪的测量，使用标准镜替换三分区镜，可以仿真正常的工作状况。

图13 光学系统实验检测Fig.13 Optical system experiment

4 结论

本文主要研究了倒立式三视场施密特望远系统的光机关键技术。采用构建数学几何模型的方法对三分区镜的设计进行了研究，结果显示，当3 个视场互相垂直时三分区镜面间夹角为133.08°，可用于多视场观测。利用有限元法对主镜重力形变进行了探究，分析了其对像质的影响，分析结果表明，主镜重力形变使得光学系统的FWHM 增大了0.02 μm。针对施密特修正镜加工误差进行仿真分析，得出加工误差对系统像质影响最大时RMS=0.039 λ。使用蒙特卡罗法对系统杂散光进行探讨，由系统PST 图可知杂散光不影响光学系统的高精度成像。对整个望远镜系统进行实验检测，得到PV=0.614λ，RMS=0.105λ。该研究为倒立式多视场施密特望远系统光机关键技术提供了技术支撑，拓展了施密特望远镜的应用范围。