悬臂拼装钢箱梁斜拉桥线形施工控制

邹雨亭

（广西交通设计集团有限公司，广西 南宁 530029）

0 引 言

悬臂拼装的钢箱梁斜拉桥施工控制过程中，需要确定主梁的无应力构形和安装线形。安装线形指的是不同吊装工况下待安装梁段悬臂端的连线。无应力构形指的是主梁在胎架上的制作构形。安装线形关注的是钢梁吊装现场线形的控制，无应力构形关注的是钢梁制作现场梁段的预制长度和梁段间预拼接角度。安装线形的意义较为明确，但考虑到钢箱主梁悬臂拼装过程中的线形受温度的影响，直接按照安装标高理论值进行钢箱主梁定位变得不可行。无应力构形却不直观且不够被重视，梁段在工厂预制时不计算无应力构形，而直接按设计构形进行预制，要么以安装线形作为无应力构形进行预制[1-3]。对于前种做法，对于全焊接接口钢箱梁可通过现场切割顶、底板钢梁长度来调整接头拼装角度，势必造成大量的现场切割工作量，而对于全栓接钢箱梁几乎很难实现。对于后者做法，显然是错误的，因安装线形为不同吊装工况下的线形，以之为基准来预制无应力构形，将会导致待安装梁段与已安装梁段间的夹角过大而造成焊缝宽度要么过宽，要么过窄，与之伴随的是焊接残余应力对结构的不利影响[4]。

综上所述，本文以南宁市某双塔钢箱梁斜拉桥为工程背景，首先以单片梁为研究对象，采用ANSYS 建立其在吊装工况下的局部模型，得出梁段在吊装过程中的变形对无应力构形几乎没有影响。其次以全桥为研究对象，以局部计算结果为支撑，采用Midas Civil 模拟施工过程建立全桥模型，通过一种巧妙的建模方法“一次性激活除合龙单元以外的所有单元（仅有刚度，无自重），荷载按实际施工过程加载”，提出了钢箱主梁无应力构形和安装线形的计算方法。最后给出了考虑温度效应影响的钢箱主梁定位标高的计算公式，为今后类似项目线形提供参考。

1 工程概述

该桥主桥跨径布置为（45+100+300+100+45）m双塔双索面连续钢箱梁斜拉桥，为半漂浮体系，桥宽39 m，桥面设双向6 车道，设计荷载为城市-A 级。上部结构为横向分离的封闭钢箱梁，两分离主梁中间采用横箱连接，箱内梁高3.438 m。索塔采用单柱式空心薄壁圆端型变截面，斜拉索按“密索”布置，标准索距为12 m，索面形状为竖琴型。桥型立面图如图1 所示。

图1 桥型立面图

根据本工程结构特点和区域地形、地貌及施工条件，钢箱梁安装施工总体思路为：采用整节段水路运输，在主塔附近靠边跨侧搭设栈桥及支架，支架上安装变幅式桅杆吊机，采用倒退拖拉和吊机前移方法拼装边跨12～3号钢箱梁，边跨钢箱梁安装完成后利用吊机安装墩顶0～1号钢箱梁，接着安装2号钢箱梁使得边跨合龙，再继续往中跨安装直至全桥合龙[5-7]（见图2、图3）。

图2 边跨钢箱梁安装方案图

图3 中跨钢箱梁安装方案图

2 梁段无应力构形的确定

钢主梁斜拉桥的悬臂拼装不能像混凝土梁段那样实现梁端间转角和悬臂端标高的较大调整，完全依靠斜拉索索力调整标高，将导致较大的内力误差。更为严重的是，必然导致主梁较大的拼接误差。误差的累积使得线形偏离理论值较多，很难再调整过来[3-4]。

在无应力构形确定之前，需要思考一个问题，即如何模拟梁段的吊装。常规做法是，吊装下一片梁时仅在前一片梁段桥面吊机前、后锚点所在节点处施加集中力，以模拟待吊装梁段的重量。这种方法建模进行线形控制忽略了一个问题，即待吊装梁段自重作用下的变形是否会对线形的控制产生影响。本文通过建立ANSYS 建立局部分析模型给予了回答。

2.1 有限元模型的建立

取4 个梁段为研究对象，采用板单元SHELL 181 模拟钢箱梁顶板、底板、腹板、横隔板及U 型加劲肋，分析吊装第5 片梁的工况下主梁的变形和拼接端口的相对变形。有限元模型及加载图如图4 所示。

图4 局部分析模型及加载图

（1）主梁变形计算

在吊装第5 片梁的工况下，作用于前4 片梁上的荷载有吊机前支点压力、后锚点拉力、斜拉索拉力和梁段自重。待吊装梁段变形如图5、图6 所示。

图5 待吊装梁段顶板竖向位移云图

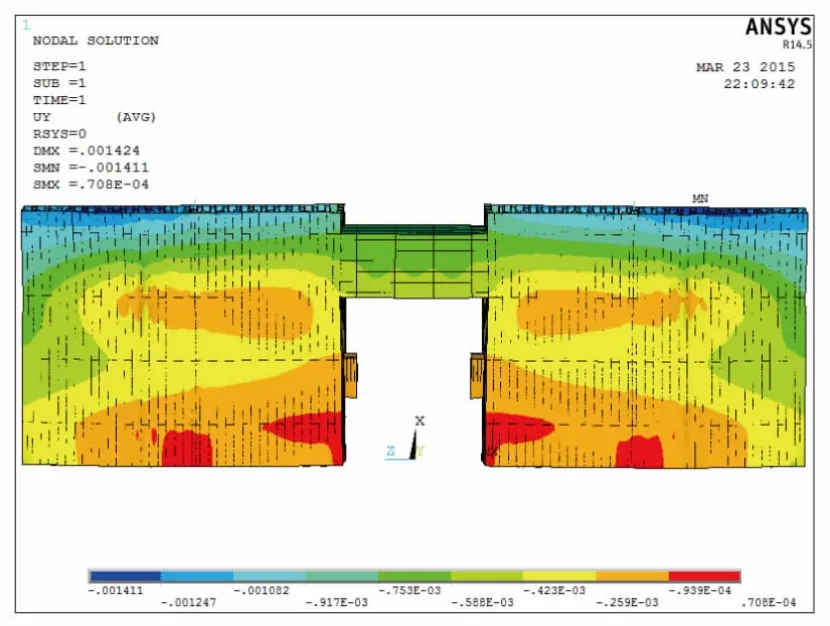
图6 待吊装梁段底板竖向位移云图

由图5、图6 可知，待吊装梁段顶板、底板（非吊点位置）在吊装过程中竖向位移最大值为1.4 mm。

由图7～ 图10 可知，待吊装梁段吊点处（横隔板位置）顶板、底板竖向位移最大值为0.75mm。

图7 前吊点处横断面顶板竖向位移

图8 前吊点处横断面底板竖向位移

图9 后吊点处横断面顶板竖向位移

图10 后吊点处横断面底板竖向位移

（2）待吊装梁段、已安装梁段端口变形计算

因左、右幅对称，为方便阐述，仅提取主梁半幅横断面部分控制点变形计算结果，控制点布置如图11 所示。

图11 变形控制点布置横断面图

由图12 可知，待吊装梁段端口最大值位于外腹板9号控制点处，为0.04 mm；已安装梁段端口与待吊装梁段端口相对位移最大值位于底板13号控制点处，为1.60 mm。

图12 梁段端口变形计算结果

综上所述，无论是待吊装梁段本身的变形，还是待吊装梁段与已安装梁段端口之间的相对变形，值均非常小，几乎可以忽略不计。这表明本桥主梁的刚度很大，在吊装过程中的变形几乎可以忽略不计。

采用Midas Civil 模拟施工过程建立全桥有限元模型（见图13）。以局部计算结果为支撑，全桥模型在吊装下一片梁时，仅在前一片梁段桥面吊机前、后锚点所在节点处施加集中力。集中力的大小根据桥面吊机的站位和待吊梁段的重量近似按“两点支撑”结构计算。同时在建模过程中采用了一种“一次性激活除合龙单元以外的所有单元（仅有刚度、无自重），荷载按实际施工过程加载”的巧妙的建模方法，考虑新生成节点的初始位移指定到沿着已成梁段切线上，以此来得到无应力线形。

图13 整体有限元模型

根据整体计算得到主梁的竖向累计位移，就可以由式（1）得出主梁无应力线形，主梁累计位移计算结果如图14 所示。

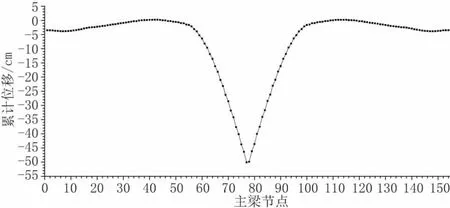
图14 主梁无应力线形（全桥）

由于岸侧过渡墩至主塔之间SA12～SA1 梁段在支架上一次性焊接成型，故相应的累计位移较少。江侧主塔至跨中之间SJ2～ SJ12 梁段为单悬臂拼装施工，相应的累计位移也较大，SJ12 梁段的前端竖向累计位移达到-50.1 cm（以向下为负）。

2.2 无应力构型的确定

主梁各控制点的无应力线形坐标求出后，就可得到梁段的无应力制作尺寸。确定梁段无应力制作尺寸有两种方法：（1）梁段采用带直角的梯形，即将梁段的一端与轴线保持垂直，另一端转动一个角度；（2）梁段采用矩形[8]。通常为了适应梁段间的折角匹配，将梁段做成带直角的梯形，梁段无应力制作尺寸如图15 所示。令第i-1 片主梁与第i 片主梁的预拼装角度为Δαi，第i-1 片主梁倾角为αi-1，第i 片主梁倾角为αi。为了适应梁段间的折角匹配，需将梁段两端或一端的接触面转动。根据简单的几何关系，可以得到如下关系：

图15 梁段无应力制作尺寸图

式中：ki、ki-1分别为第i 片主梁与第i-1 片主梁的斜率；hs、hx分别为截面的上下形心距；L（i-1）o为第i-1 片主梁轴线的无应力长度；L（i-1）s、L（i-1）x分别为顶、底板的无应力长度。

工厂预制过程中，还需考虑焊缝的宽度和收缩量的影响，一般由厂家根据经验或实测值给出。最终的制作尺寸应减去梁段两端的焊缝宽度，再加上焊缝收缩量[9-10]。

3 梁段安装线形的确定

如前所述，主梁的安装线形指的是不同吊装工况下待安装梁段悬臂端的连线，对于线性结构，主梁的设计线形坐标与安装线形坐标之间的关系，如下所示：

根据整体计算得到主梁的竖向累计位移，就可以由式（3）得出主梁的安装标高，详见表1。可见，为达到设计线形，主梁中跨跨中预抬值为244 mm（向上）。

表1 S J 10 梁段定位时定位标高计算单位：mm

4 考虑温度影响的钢箱梁定位标高的修正

温度对线形控制的影响分为昼夜温差和季节性温差，而在施工过程中起作用的是昼夜温差产生的沿梁高变化的温度梯度[11-13]。本文提出了一种考虑温度影响的钢箱梁定位标高的确定的方法。

设第i 片主梁起吊匹配时，第i-1 片主梁前、后端标高实测值为，理论值（不考虑温度效应影响）为，则温度对前、后端标高影响若要保证定位时第i-1片主梁与第i 片主梁之间夹角与理论值相同（未考虑顶、底板焊缝收缩差影响），则第i 片主梁安装标高的调整量按式（4）确定：

式中：Li-1、Li分别为第i-1 片及第i 片主梁的长度。

新梁段起吊匹配时，主梁上各节点的标高值计算公式如下：

式中：H1为节点的设计高程；Δ1为节点自生成到最终成桥状态的竖向累计位移值；Δ2为节点自生成到当前施工阶段的竖向累计位移值。

以南岸的SJ10 梁段的标高控制为例，设梁段SJ10 定位时，SJ9 前、后端实测标高分别为、，梁段长度L9=L10=12 m，其余相关参数见表1。由表1中数据可得SJ10 实时定位标高为

利用上述计算公式，在施工现场即使结构的温度场发生变化，也能实时求出梁段的定位标高，给施工过程中线形的控制带来极大的便利。

5 结 语

（1）本文论述了钢箱主梁无应力构形及安装线形的相关概念及计算方法。

（2）本文提出了在考虑温度影响的梁段定位标高的修正公式，并将其运用于工程实例，简化了施工控制工作，提高了施工控制的效率，并取得了良好的控制效果，可以作为今后类型项目线形控制参考。