基于基线比值法的多基线相位干涉仪解模糊算法研究
徐文君,赵荣琦,刘志永
(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)
0 引 言
对威胁辐射源进行精确方位测量是实现小型运动平台单站定位的前提,因此精确测向对小型运动平台电子战具有重要的意义[1]。小型运动平台对电子战设备的安装尺寸、结构重量、功耗以及成本等因素要求较为苛刻,基于比幅体制的模拟多波束系统或者数字多波束系统设备体积通常较大且成本较高,难以满足小型化平台应用需求。干涉仪测向系统具有测向精度高、设备量小、实时性高等优点,在电子战设备中广泛应用[2-3]。干涉仪测向系统的测向性能及天线基线长度和测向算法密切相关,为保证测向精度,在一定相位测量误差的情况下,基线长度必须满足一定的要求。干涉仪测向系统可通过长、短基线相互配合解模糊[4-5],利用短基线无模糊的相位差测量值,基于长、短基线比,获取长基线的无模糊相位差值。该方法正确解模糊的概率受长、短基线相位差测量误差影响。当相位差测量误差超差时,将会导致解模糊失败,在方位测量结果上表现为方位测量“飞点”。在实际测向天线阵构造时,常常需要构造多组长、短基线,以满足测向精度要求。其中最短基线一般需小于最短半波长,以保证无模糊测向。电子战系统一般为宽带系统,天线尺寸由最大波长决定,受天线物理尺寸限制,需要构造虚拟基线以满足最短基线要求。虚拟基线的应用导致基于长、短基线的逐级解模糊算法的相位容差进一步降低。
基于余数定理,通过构造基线长度为互质数比的天线阵,利用最小均方误差准则进行多维搜索,可以实现相位解模糊[6]。但是在基线组数较多时,存在运算量大、解算实时性差的问题。利用多组基线间的互质关系,可以将多维搜索转换为多次二维搜索,能够在一定程度上降低计算量。但是多次二维搜索的计算量依然较大。令所有相邻基线长度之比为固定值且所有基线长度整数比的最大公约数为1,这样通过多次一维搜索即可实现相位解模糊[7]。本文结合实际工程应用,给出了基于多次一维搜索的基线比值法的基本原理,分析了正确解模糊的条件,通过仿真验证了算法的有效性,为长基线高精度干涉仪测向天线阵的工程优化设计提供了理论设计依据。
1 干涉仪阵列解模糊模型

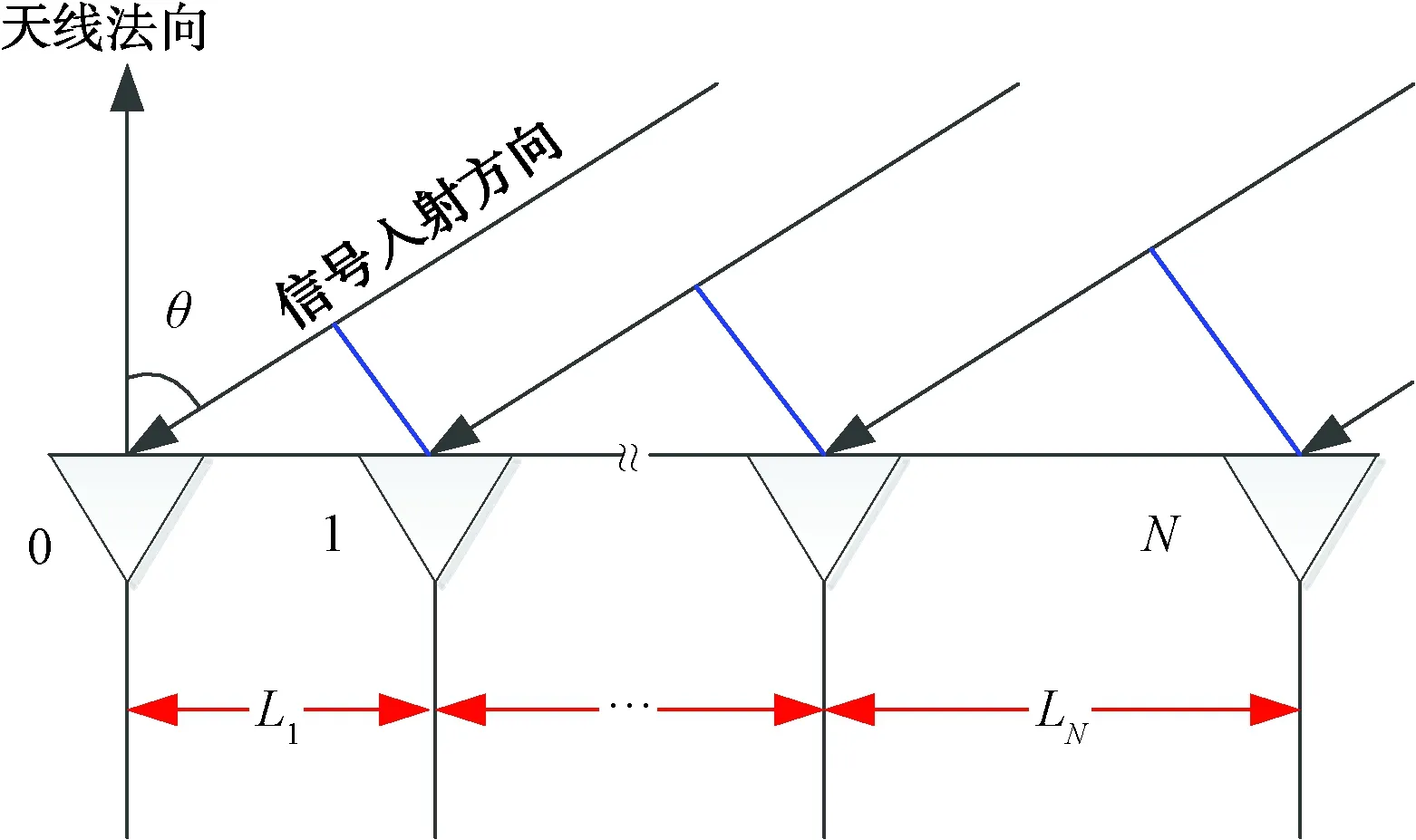
图1 干涉仪测向天线阵排布示意图
假设辐射源和干涉仪测向天线阵的距离关系满足远场条件,则辐射源信号可以看作是平面波入射,记辐射源信号入射角度为θ,则各基线由于路程差引起的相位差为:
φn=2πLnsinθ/λ
(1)
式中:n=1,2,…,N。

(2)
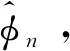
(3)
结合式(1),可以得到:
(4)

(5)
当λ取最小值λ0时,kn具有最大的取值范围,此时有:
(6)

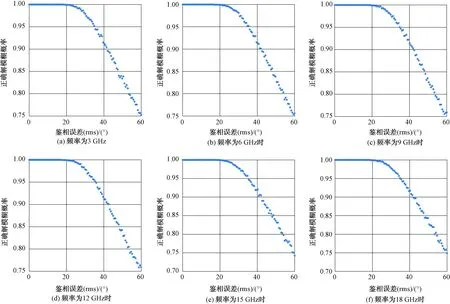
-Pn/2+1/2 (7) kn为在(-Pn/2,Pn/2)范围内的整数,得到kn的取值后,信号入射角为: (8) 以上是不存在相位差测量噪声时的信号入射角估计方法,存在相位差测量噪声时,需要在最小均方误差准则下对式(3)进行N维搜索,计算量较大。 首先讨论双基线干涉仪系统,此时N=2,则: (9) 需要说明的是,对于基线Ln和Ln+1,其最大公因子为GCD(Pn,Pn+1),则满足要求的相位模糊数共有GCD(Pn,Pn+1);对于基线L1、L2、…、LN,其最大公因子为1,因此,存在唯一一组满足要求的相位模糊数。 根据相邻两两基线可以确定各基线所有可能的相位模糊数,取所有基线相位模糊的共同解,该解即为最终确定的真实模糊数。主要步骤如下: 根据以上步骤,只需要进行N-1次一维搜索,就能够得到真实相位模糊,有利于实现实时计算。 对于双基线系统,假设基线鉴相误差分别为Δφn、Δφn+1,则正确解模糊的条件为: (10) 对于如图1所示的多基线系统,可以看成由多个双基线系统组成,正确解模糊的条件为所有的基线鉴相误差必须满足: (11) 假设各基线鉴相误差相同,都为Δφ,则: (12) 对于某机载电子侦察系统,要求测向精度优于1°(rms),频段范围为3~18 GHz,干涉仪测向精度计算公式如下: (13) 根据上式,基线鉴相误差Δφ越小,测向精度Δθ越高;最大基线长度Lmax越长,测向精度越高;信号入射角θ越小,测向精度越高;信号波长λ越短,测向精度越高。 假设干涉仪系统各基线鉴相误差相同,影响鉴相误差的主要因素包括天线相位不一致性、微波通道不一致性、数字接收机的不一致性[8-9]。综合考虑,假设经过校正后,总鉴相误差Δφ为15°,信号波长λ最大值为100 mm,入射角最大值取为30°,可以得到所需最长基线应不小于550 mm。 根据正确解模糊条件,p+q<12,p、q互质,取p=5,q=6。 最短基线λmin=16.67 mm,取λ0=16 mm。 取N=3,则基线比为25∶30∶36,L1、L2、L3基线长度分别为200 mm、240 mm、288 mm,最长基线长度为728 mm,满足测向精度要求。 分析不同鉴相误差对正确解模糊的影响,鉴相误差Δφ服从正态分布,取值范围为0~60°,信号入射角分别为0°和30°,频率点分别为3 GHz、6 GHz、9 GHz、12 GHz、15 GHz、18 GHz,分别独立进行10 000次蒙特卡洛试验,记录正确解模糊的次数,正确解模糊概率为正确解模糊次数和总试验次数的比值,仿真结果如图2、图3所示。 图2 入射角为0°时相位解模糊概率仿真结果 图3 入射角为45°时相位解模糊概率仿真结果 图4 工作流程 可以看出,在鉴相误差不超过20°时,在不同入射角和不同频率下,正确解模糊概率均能达到100%;随着鉴相误差的增加,正确解模糊概率越来越低。因此工程设计中,必须对鉴相误差进行控制,以保证干涉仪系统能够正确解模糊。为了降低鉴相误差,在进行干涉仪系统设计时,必须对天线单元、微波通道和数字接收通道的相位一致性进行约束。干涉仪系统设计完成后,还可以通过相位校准的方式对系统相位误差进行补偿。微波通道和数字接收通道是没有方向性的,其相位校准可以通过自检源注入的方式进行;而天线单元是有方向性的,其相位校准只能在暗室通过辐射法进行。校准时,信号入射角是已知的。但是实际中信号入射角只能通过干涉仪系统测量后得到,可以根据测量得到的信号入射角确定补偿值,再得到补偿后的最终信号入射角,也可以根据一定的优化搜索策略选择最优补偿值。但是该方法的运算量相对较大,实时性会受到影响。 本文针对多基线干涉仪系统相位解模糊问题,分析了基于基线比值法的相位解模糊算法,通过构造相邻基线比值固定且所有基线比值不可约的天线阵列,根据其天线阵列结构特点,可以只通过多次一维搜索就能够确定所有基线相位模糊数,具有较好的实时性。给出了该方法相位解模糊条件,结合实际应用需求,给出了基于基线比值法的干涉仪系统设计实例。通过仿真分析,验证了系统的相位解模糊特性,在满足相位解模糊条件的情况下,能够实现100%相位解模糊。随着鉴相误差的增大,解模糊概率逐渐降低,这将导致系统测向精度下降。除了尽可能降低系统鉴相误差外,还有一种有效的方式是对是否成功解模糊进行识别判断。如果判断为解模糊失败,则丢弃该测向值,以保证测向精度。这也是后续需要继续研究的方向。2 无模糊相位差求解步骤

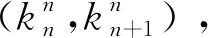
3 正确解模糊条件
4 多基线干涉仪设计实例
5 仿真分析

6 结束语

