对干涉合成孔径雷达的干扰研究

许 强,逯 程,张瑞玲,周姝婧

(1.中国船舶集团有限公司第七二三研究所,江苏 扬州 225101;2.海军装备部,北京 100084)

0 引 言

干涉合成孔径雷达是一种具备高程成像能力的高分辨率雷达,具备全天候、大范围、高精度对地貌进行三维测绘的能力,其在军事、经济和科研等领域已广泛应用。目前,国外已有大批星载和机载的干涉合成孔径雷达投入使用。例如星载的TerraSAR-X(TSX)、TanDEM-X、TanDEM-L、Radarsat-1&2&3、ALOS-2等;以及机载的E/F-SAR、P3-SAR、TOP-SAR、Pi-SAR等。因此,开展对干涉合成孔径雷达干扰技术的研究显得极为迫切[1]。

干涉合成孔径雷达的干扰技术就是所有针对敌方雷达所采取的包括扰乱、破坏、欺骗等战术和战略措施,从而让合成孔径雷达无法正常干涉成像的技术。由于干涉合成孔径雷达拥有一定的穿透能力、全天时、全天候工作能力和成像速度快、精度高等优点,因此具有极强的应用价值[2]。对于干涉合成孔径雷达的干扰技术研究将成为未来发展的重要课题[3]。

1 干涉合成孔径雷达成像原理

干涉合成孔径雷达实现高程成像,主要采用2种方法。一种是单天线双航过,即在平台上布置一个雷达天线对目标点在不同高度上进行2次SAR成像,并从2次成像图像中经过相对应的算法得到高程图[4]。另一种是两天线单航过,在同一平台上布置高度不同的2个天线,其中一个天线发射并接收雷达信号,另一个天线不发射只接收雷达信号,利用两天线与目标点之间由距离差产生的相位差,计算得到目标的高度,从而得到目标区域的高程图[5]。

本文以机载平台的干扰合成孔径雷达为例,分析高程成像的原理,如图1所示。

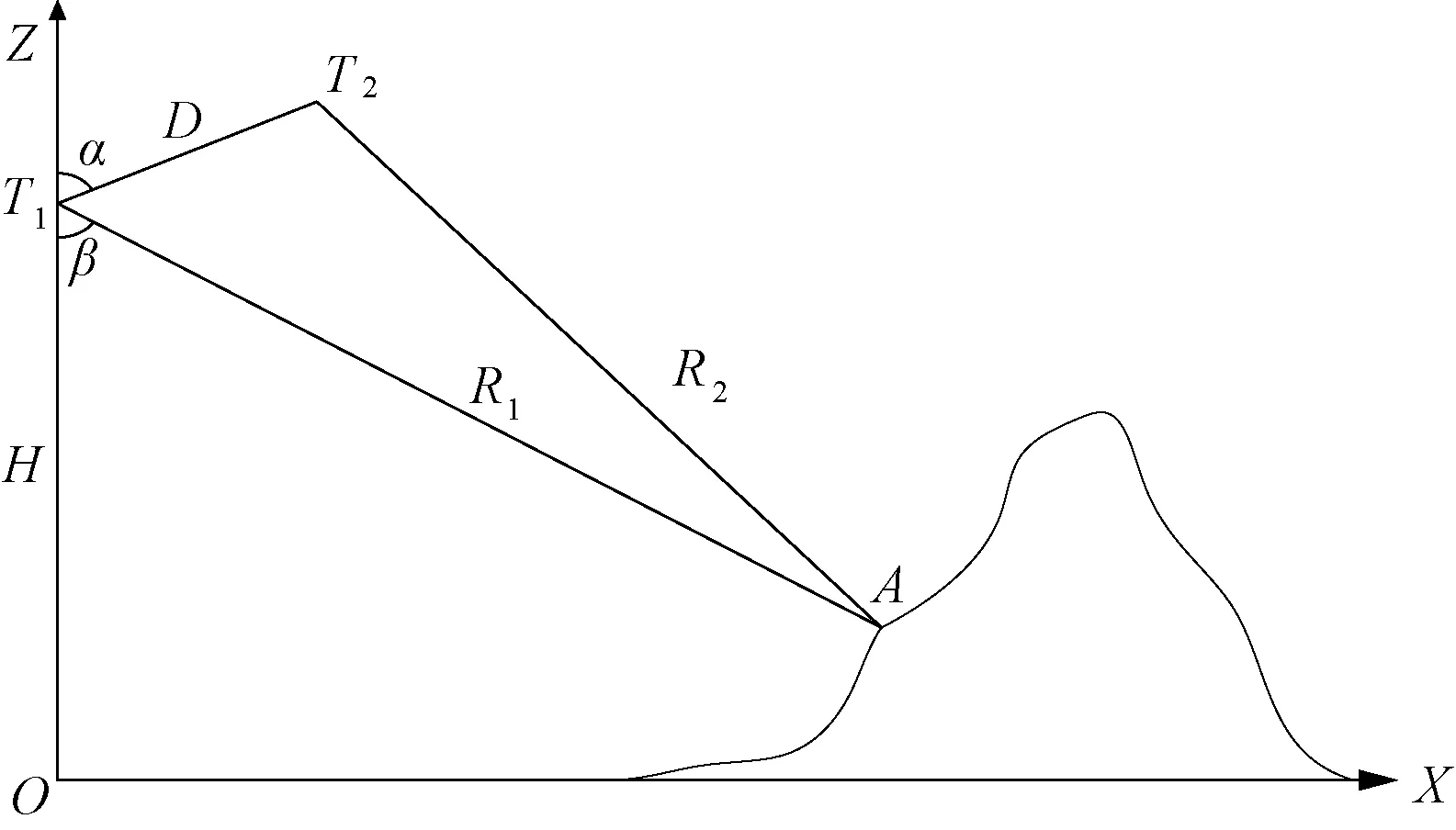
图1 干涉合成孔径雷达与目标的几何示意图

图1中,T1和T2分别表示机载平台上的两天线,R1和R2分别为两天线到目标点A的斜距。α为两天线间的基线D与高度H的夹角,H为载机成像时刻的飞行高度,β为斜距R1和飞行高度H间的夹角,即天线的下视角,同时α、β和H均可以通过载机传感器或直接测量得到。

若经两天线成像得到的两复数图像分别为P1和P2,并且复数图像已经过图像配准,则对两复数图像做共轭处理可得干涉图[6]。

A点在复数图像P1上的像素点为:

QP1=|A1|ejφ1

(1)

A点在复数图像P2上的像素点为:

QP2=|A2|ejφ2

(2)

A点在干涉图上的像素点为:

Q=QP1QP2*=|A1||A2|ej(φ2-φ1)

(3)

两天线收到的雷达回波信号的相位由两部分构成,一部分是由天线与目标点之间的距离造成的相位差,另一部分是由于目标点向不同方向散射雷达信号造成的相位差。因此,目标点在两复图像上的相位值可以表示为:

(4)

(5)

式中:φP1和φP2是目标点向不同方向散射雷达信号造成的相位差。

由于R1>>D,目标点到两天线的夹角也很小,可近似认为φP1和φP2的相位相同,即φP1≈φP2。由式(4)和(5)可得到干扰相位差:

(6)

根据三角余弦定理可得:

(7)

因为R1>>D,则式(7)可简化为:

(R2-R1)≈Dsin(β-α)

(8)

由式(8)和式(6)可得:

(9)

根据图1中雷达与目标的几何关系,可以由式(9)和斜距R1得到目标点A的高度:

h=H-R1cosβ

(10)

2 对干涉合成孔径雷达的调频干扰研究

2.1 原理分析

本文提出一种对干涉合成孔径雷达的有效干扰方法,即调频干扰。调频干扰技术是指在收到的雷达信号基础上增加额外的频率调试信号的技术,干扰信号的表达式为:

(11)

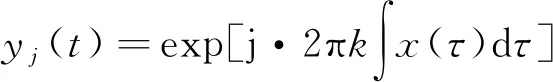
fj(t)=f0+μt+kx(t)

(12)

由式(12)可知,干扰信号的频率是由线性调频和调制频率两部分组成,调制频率依据选择的调制方式不同可以由正弦波、锯齿波和高斯噪声等多种信号构成。对调频干扰信号来说,距离向和方位向的频谱分析相似。以正弦调频信号为例,分析其对干扰合成孔径雷达的影响。

当调制信号为正弦波时,信号的表达式为:

x(t)=ajsinωjt=ajsin2πfsint

(13)

式中:aj为调制幅度;ωj=2πfsin为正弦信号的角频率,fsin为正弦信号的周期频率。

因此,调频干扰信号的表达式为:

(14)

式中:kj=2πkaj/ωj。

调频干扰信号的时频特性曲线如图2所示。

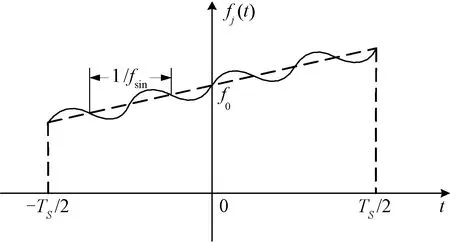
图2 正弦调频信号的时频示意图

(1) 当kj<<1时,可近似认为cos(kjsinωjt)≈1,sin(kjsinωjt)≈kjsinωjt,则式(14)可简化为:

(15)

由式(15)可知,此时干扰信号表示为3个线性调频信号,即1个雷达信号和2个频偏为±fsin的信号。干扰信号匹配滤波后,得到原脉压信号和2个正负频偏的脉压信号。此时,正频偏的信号优先于雷达信号脉压输出,能够产生前移的距离欺骗目标;负频偏的信号滞后于雷达信号脉压输出,产生滞后的距离欺骗假目标。

综上所述,此时干扰仅能在距离向上产生3个假目标点,不能产生大面积的干扰,且两侧点的幅度均小于主信号。

(2) 当kj>>1时,将式(14)中的yj(t)=exp(j·kjcosωjt)级数展开可以得到:

(16)

式中:Li(kj)为i阶第一类贝塞尔函数。

可知,其频谱由线性调频信号的频谱及其无数个偏移量构成,频偏为±ifsin。频偏相对应的幅度为A·Li(kj)。经匹配滤波后,除了能得到主信号的脉压信号以外,还存在各个分量的脉压信号,即输出为无数个sinc脉冲串。因为在此过程中生成了多个频率分量,所以干扰信号的频率带宽会比原有主信号的频率带宽宽。

在方位向上的分析,与距离向分析相类似,只要将距离向调频干扰信号的参数更改为方位向的参数即可。经过方位匹配滤波后,可以得到方位向的部分处理增益,从而达到两维联合干扰的目的。

2.2 实验仿真

本文利用Matlab自带的peaks函数产生的高程图作为原始图像,仿真了调频干扰对InSAR成像的影响,假设复图像对是完全配准的。

仿真参数设置为:信号载频为9.5 GHz,脉冲重复频率为500 Hz,脉宽为15 μs,调频带宽为100 MHz,下视角β=50°,飞机初始时刻的高度为15 000 m,速度为vx=1 000 m/s,vy=0 m/s,vz=0 m/s,加速度ax=0 m/s2,ay=0 m/s2,az=0 m/s2,斜视角β=85°。仿真结果如图3和图4所示。

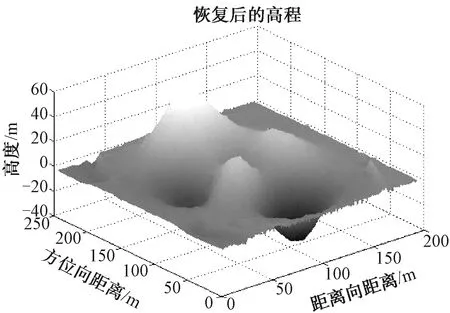
图3 合成孔径雷达干涉成像的高程图

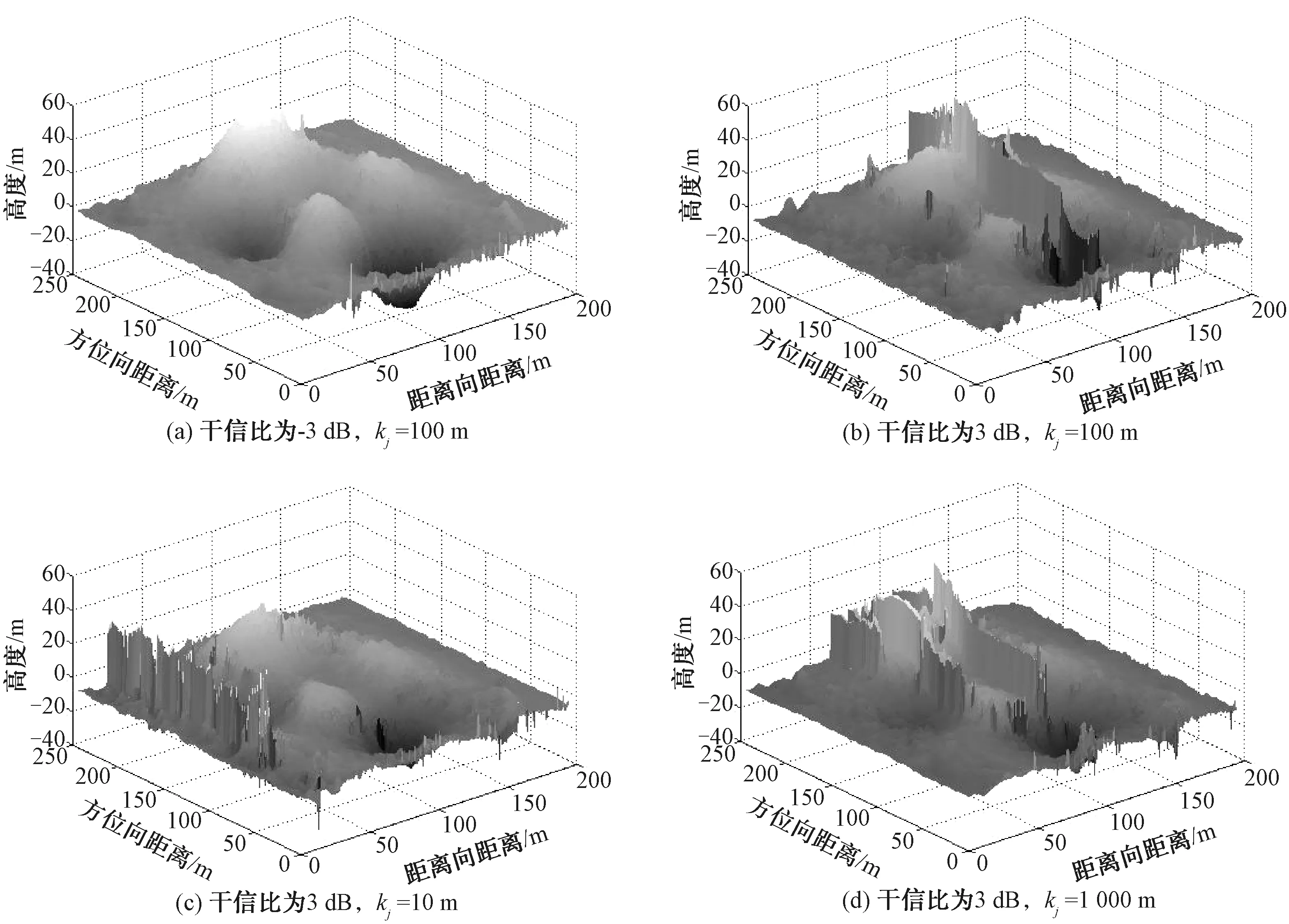
图4 正弦调频干扰的成像结果

由图3和图4可以看出,正弦调频干扰能够对合成孔径雷达的干扰成像造成遮盖干扰效果。通过设置干信比以及调制参数可有效对干扰产生影响。其中干扰比即干扰的功率越大,干扰效果越好;调制参数越大,干扰效果越好。且在高程图中能够明显看到距离向上能够产生多条遮盖条带。

3 结束语

本文首先介绍了合成孔径雷达干涉成像的原理,利用两复图像对的相干性,通过干涉处理得到目标点的相位,从而计算得出高度信息,研究了调频干扰对合成孔径雷达干涉成像的信号影响。研究表明:正弦调频干扰能够对合成孔径雷达干涉成像实施有效干扰,并且干扰功率以及调制参数的设置均能够对干扰效果产生影响。