基于代价敏感神经网络集成模型的类别不平衡问题研究

张俊杰, 曹 丽

(合肥工业大学 数学学院,安徽 合肥 230601)

类别不平衡问题是指数据集的各个类别的样本数差异明显,即某些类别的样本数远小于其他类别的样本数。类别不平衡问题普遍存在于各个领域,如疾病检查、软件测试、病毒入侵、信用欺诈等。传统的分类模型偏向对大类别样本的学习而忽略小类别样本的学习;但是在疾病诊断等领域,小类别样本通常才是关注的重点,因此类别不平衡数据问题成为数据挖掘领域热点问题之一。针对该问题,目前常用的解决方法主要集中在数据采样、模型选择和性能评估等方面。

在数据采样方面,上采样和下采样是处理类别不平衡问题的常用方法。然而上采样容易增加噪声样本的比例,导致模型出现过拟合;下采样容易丢失重要样本,导致模型出现欠拟合。因此文献[1]对上采样方法进行了改进,提出SMOTE方法,但是该方法容易产生噪声样本,影响模型的分类效果。

在模型选择方面,解决类别不平衡问题常采用集成模型,如SMOTEBoost模型[2]。该模型在每次迭代过程中通过SMOTE方法合成新小类别样本,改变样本类别分布,以增加再迭代时模型对小类别样本的学习次数。类似的集成模型还有RUSBoost模型[3]和CUSBoost模型[4]。但这些串行模型的训练样本选择与前一轮模型的学习效果直接相关,并非独立采样,一旦当前模型的误差小于阈值,则当前模型学习停止,容易导致早停,影响集成模型效果。还有学者从代价敏感的角度解决类别不平衡问题,解决方法大致可分为类依赖代价矩阵法和样本依赖代价矩阵法。类依赖代价矩阵法主要有代价敏感神经网络[5]、Hard-Ensemble模型[5]和Soft-Ensemble模型[5]。样本依赖代价矩阵法主要有样本依赖代价敏感学习决策树算法[6]和样本依赖代价敏感学习Adaboost算法[7]。

在性能评估方面,当大类别样本量远大于小类别样本量时,例如当类别比例为1∶99时,若将全部样本判定为大类别样本,则准确率达到99%,但是此时的准确率已无参考意义和评估价值。因此,在类别不平衡问题中通常使用如下的性能评估标准:精准率P、召回率R、P-R曲线、F1值以及ROC曲线等。文献[8]将P-R曲线和ROC曲线做对比,在数据类别不平衡的条件下,ROC曲线的性能评估优于P-R曲线,但ROC曲线不能很好反映误分类代价情况。

针对上述问题,本文提出代价敏感神经网络集成(cost-sensitive neural network ensemble,CSNN-Ensemble)模型。首先通过多次随机下采样方式,每个基学习器学习不同的训练样本,防止样本丢失;其次考虑误分类代价,用代价敏感神经网络作为基学习器,实现更佳的分类效果;然后结合并行集成学习的思想,降低基学习器之间的关联性;最后通过UCI上9组二分类数据集进行几种集成模型的对比实验,结果表明该模型具有一定的有效性和实用性。

1 代价敏感神经网络原理

代价敏感学习是根据不同误分类产生的不同代价,寻找使得模型的期望损失代价最小的机器学习方法;在代价敏感学习过程中,代价矩阵至关重要,决定着模型的分类结果。假设数据集共有n种类别,代价矩阵是由误分类代价所构成的矩阵,用(Ci,j)n×n表示代价矩阵,其中Ci,j表示第i类误分为第j类的代价。特别地,规定Ci,i=0。基于代价敏感原理,本文沿用文献[9]给定的代价矩阵的3种类型:

类型1存在唯一的c,当j=c时,有Ci,j>h,并且对所有j≠i,Ci,j≠c=h;对j≠c和Cc=h,定义Ci=Ci,c。

类型2对所有j≠i,有Ci,j=hi≥1.0;定义Ci=hi。

3种类型中的Ci表示第i类代价。

(1)

其中,η为归一化参数。

2 代价敏感神经网络集成模型原理

集成学习的基本思想是将多个独立的、单一的基学习器按照某种结合策略有机地结合起来,从而获得更准确的预测模型。目前主要的集成学习范式有提升(Boosting)和装袋(Bagging)2种。Boosting集成范式采用串行模式,每轮训练集的选择与前一轮基学习器的学习效果相关,且基学习器以加权组合的方式构造集成模型。Bagging集成范式采用并行模式,各个基学习器之间独立存在,模型相对简单,能提高稳定性差的基学习器的预测精度。

本文采用Bagging集成范式构造代价敏感神经网络集成模型。首先对原始数据集中大类别样本N进行多次有放回的随机下采样,分别与小类别样本M合并,构造m个训练数据集;其次对每个训练数据集分别训练BP神经网络,引入代价矩阵(Ci,j)n×n后,构造m个代价敏感神经网络;最后对所构造出的m个代价敏感神经网络进行并行组合。CSNN-Ensemble模型的算法流程如图1所示,算法步骤如下:

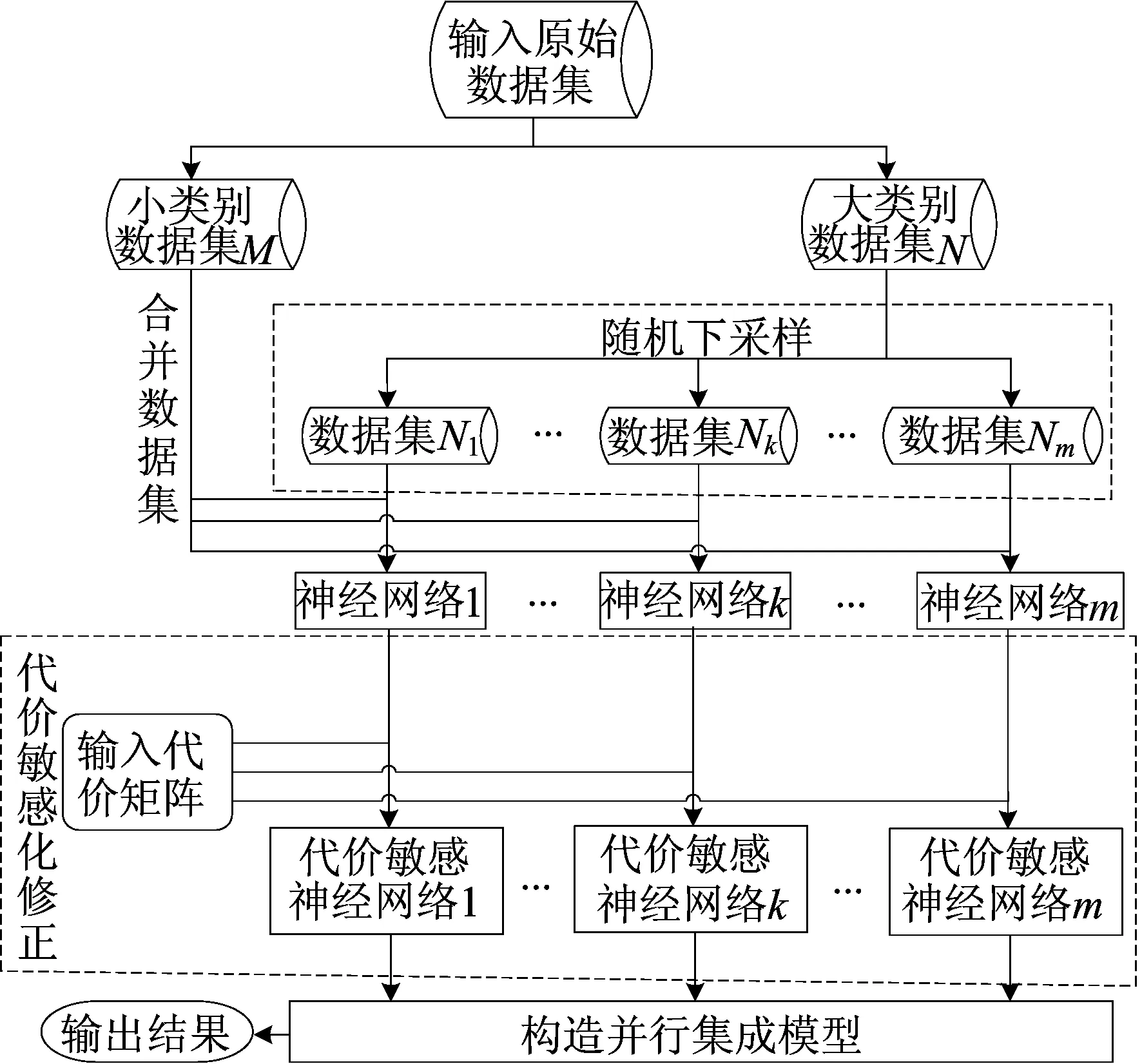
图1 CSNN-Ensemble模型的算法流程

1) 输入小类别样本M、大类别样本N、基学习器数量m以及代价矩阵(Ci,j)n×n;

2) 使用有放回的独立随机下采样方法,从N中采样得到m个样本子集Nk,使Nk的样本量与M的样本量相等,且Nk⊂N,k=1,2,…,m;

3) 将m个下采样子集Nk分别与M合并,训练出m个神经网络Hk;

4) 对每个Hk,分别引入代价矩阵,将其概率值与之相对应的误分为其他类的代价相乘并求和,归一化计算后得到代价敏感神经网络Hk′;

CSNN-Ensemble模型以代价敏感神经网络作为基学习器,模型相对简单、复杂度低,且采用并行组合策略,能够降低模型的方差,增加模型鲁棒性。

3 实证分析

3.1 性能评估方法介绍

对于分类问题,分类准确率常常作为最重要的评价指标,但是在类别不平衡数据中,因为这种评价方法通常对大类别样本偏袒严重,而忽略对小类别样本的识别率,所以分类准确率对于类别不平衡数据往往不太合理。因此,本节将混淆矩阵介绍F1值、ROC曲线和代价曲线作为模型性能度量方法。混淆矩阵形式见表1所列。

表1 混淆矩阵

精准率P、召回率R和假正例率RFP定义分别如下:

(2)

(3)

(4)

其中,召回率也称为真正例率RTP。

F1值计算公式如下:

F1=2PR/(P+R)

(5)

ROC曲线是以假正例率RFP为横坐标、真正例率RTP为纵坐标绘制而成。定义ROC曲线下方面积为AUC值,模型分类性能的优劣与AUC值的大小成正比。代价曲线是一种考虑了误分类代价的分类性能度量方法;它是以正例概率代价PC(+)为横轴,以归一化代价NEC为纵轴绘制而成。PC(+)和NEC定义如下:

(6)

(7)

其中:P(+)、P(-)分别为样本中正、负例的概率;C(-|+)为正例误判为负例的代价;C(+|-)为负例误判为正例的代价;假反例率RFN=1-RTP。根据式(6)、式(7),将归一化代价化简为:

NEC=(1-RFP-RTP)PC(+)+RFP

(8)

由式(8)可知,归一化代价和正例概率代价是一种线性关系,且ROC曲线上的每个点(RFP,RTP)对应一条归一化代价直线。连接归一化代价直线的最小值点所形成的曲线即为代价曲线。定义代价曲线下方的面积为期望总体代价,模型分类性能的优劣与期望总体代价的大小成反比。

3.2 实验结果分析

本文选出UCI数据集中9组二分类数据作测试验证,数据信息见表2所列。

表2 数据集信息

有个别数据集中含有多种类别样本,选择其中一个样本量少的类为小类别样本,其余类别合并成大类别样本。

在二分类问题中,3种代价矩阵类型没有区别,且都可以用第3种类型进行表示[5],因此本文使用第3种类型代价矩阵训练CSNN-Ensemble模型,对数据标准化处理后作为输入数据进行模型验证。

在9组数据集中,分别将GBDT模型、Random-Forest模型、Easy-Ensemble模型、Bagging模型、Adaboost模型与CSNN-Ensemble模型做对比,并采用10折交叉验证方式验证模型的有效性。

其中:Easy-Ensemble模型[10]的基学习器为Adaboost模型;Bagging模型的基学习器为BP神经网络模型;Adaboost模型的基学习器为决策树模型。通过对比6种模型的F1值、ROC曲线和代价曲线完成性能评估。6种模型的ROC曲线和代价曲线如图2、图3所示;F1值、AUC值和期望总体代价的10折交叉验证结果见表3～表5所列。

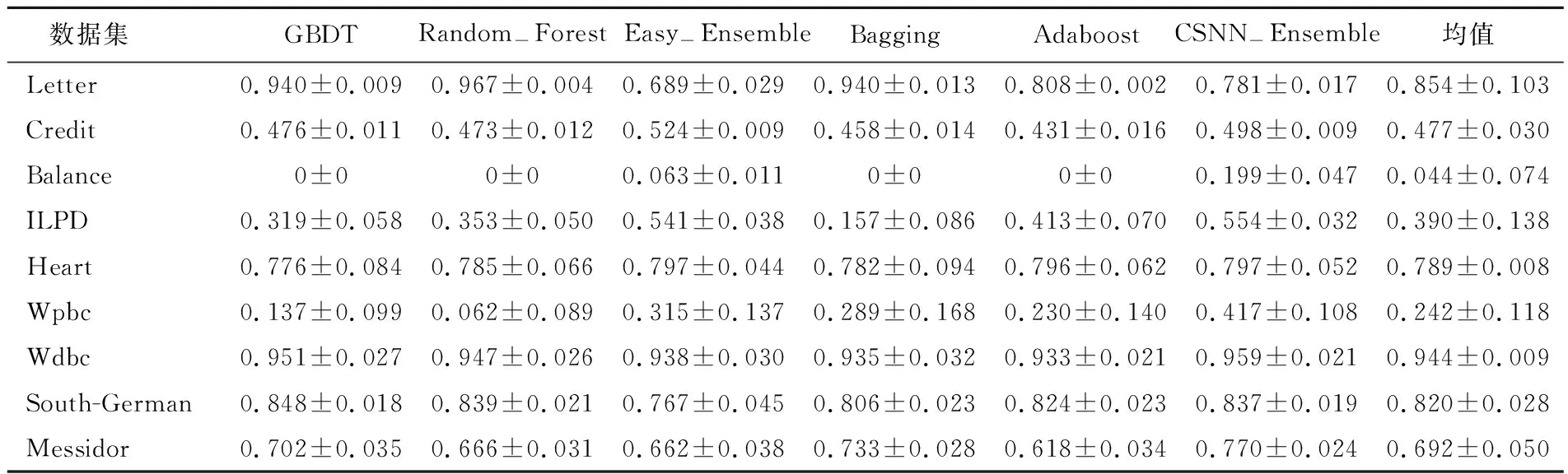
表3 6种模型在9组数据集中的F1值

图3 6种模型在9组数据集中的代价曲线

实证结果表明,在处理类别不平衡数据问题时,Adaboost模型在9组数据集中表现效果较差,而与之相比的其他5种模型都或多或少地表现出较强的分类性能。

F1值作为精准率和召回率的调和平均数,F1值越大,模型性能越优。从表3可以看出,在F1值的平均值大于0.8的数据集中,GBDT模型、Random-Forest模型、CSNN-Ensemble模型表现出相对较好的性能;而在F1值的平均值小于0.8的数据集中,Easy-Ensemble模型和CSNN-Ensemble模型的性能较优;这2种模型都是使用下采样方法进行数据处理,因此下采样处理类别不平衡问题是合理的。

从表4和表5可以看出,只有Balance数据集中6种集成模型结果相差较大,这可能是样本特征属性和样本量较少的原因。在9组数据集中,仅CSNN-Ensemble模型的AUC值和期望总体代价优于平均值。究其原因不难发现,该模型在基学习器中引入代价因子后,改变了分类阈值,使模型对样本的分类结果偏向于小类别样本。

表4 6种模型在9组数据集中的AUC值

表5 6种模型在9组数据集中的期望总体代价

为了进一步从整体上评价模型优劣,对F1值、AUC值、期望总体代价3种性能结果采用Friedman检验,检验结果见表6所列。

从表6可以看出,CSNN-Ensemble模型均获得了最低的平均序值。根据3种平均序值计算的Friedman检验值τF分别为2.532、4.857、6.098,均高于在显著性水平α=0.05下的临界值2.449,于是拒绝“所有模型性能相同”的假设;因此CSNN-Ensemble模型优于其他模型。

4 结 论

在类别不平衡数据问题研究中,针对下采样方法导致的样本丢失和分类过程中存在误分类代价不等问题,本文结合代价敏感神经网络与并行集成思想,构造了CSNN-Ensemble模型。首先通过多次随机下采样,每个基学习器能学习不同的训练样本,防止样本丢失;然后在此基础上,构造以代价敏感神经网络为基学习器的并行集成模型,降低数据扰动对基学习器的影响。该模型以投票的方式进行决策,保证了所有基学习器的权重相同。实验结果表明CSNN-Ensemble模型有效提高了分类性能。然而,如何对基学习器采用加权组合的方式构造集成模型将是下一步的研究方向。