大长径比弹体侵彻混凝土结构强度、稳定性及振动特性研究
郑卓扬,武海军,董 恒,李 萌,皮爱国
(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
0 引言
随着当前深层防御系统的研究,对深层钻地武器的侵彻能力提出了更高的要求。在发射速度及弹体材料强度受到限制时,为进一步提升侵彻能力,提高结构的长径比成为有效的手段,同时为达到一定的装填比和毁伤能力,对弹体结构的壁厚也有一定的要求。20世纪90年代美航空武器中心和空军研究实验室牵头开发了一种具有典型大长径比结构的动能侵彻弹(small diameter bomb,SDB),极大的提升了空中武器平台的挂载和侵彻能力,该弹具有大长径比(一般高达10以上)、高曲径比、小无量纲壁厚的结构特点,在打击目标时面临着更为极端的过载环境,对其结构设计和弹目交汇模式提出了更为严苛的要求。
SDB在侵彻目标时极易出现2类结构问题:一是结构强度问题,即弹体结构在侵彻过程特别是侵彻初期的结构完整性问题;二是结构稳定性问题,即结构在冲击载荷下抵抗塑性变形的能力,如弯曲变形,剪切变形等,这是当前大长径比结构弹体设计时广泛关注的焦点问题。陈小伟[1]分析了圆柱壳弹体斜侵彻混凝土的受力情况,针对不同撞击速度的细长中空弹体,分析得到不出现弯曲破坏的弹体最大临界倾角和最小壳体壁厚。皮爱国[2]利用刚塑性自由梁模型分析了大长细比弹体斜侵彻混凝土靶的动力学响应,基于压弯载荷联合作用分析,给出了抗弯极限壁厚要求。张欣欣[3]对刻槽短粗弹体斜侵彻混凝土靶的结构响应展开了研究,将其简化为变截面自由梁,得到了不同条件下屈服函数分布规律,但以上学者的研究均未考虑攻角及应力波效应的影响。王一楠[4]对中低长径比,无量纲壁厚在0.2以上的动能侵彻弹以小攻角高速侵彻混凝土靶的弹体弯曲展开了理论分析,结论与实验现象有较好的一致性,但在微小攻角范围内采用阻力等效分解的方法存在一定的局限性。
弹体在强冲击载荷下必然会产生应力波并引起结构的振动响应。徐文铮等[5]的研究表明,弹体在整个侵彻过程中都会伴随着轴向振动,弹体实际过载为刚性过载上叠加振动过载,并且在弹体的不同位置会表现出不同的振动特性,装药会在振动过载影响下发生轴向压缩拉伸、密度变化及损伤演化等现象。彭家忠[6]指出长径比的增加会降低弹箭的抗弯强度及横向弯曲固有频率。易兴利[7]研究了大长径比火箭弹在瞬态冲击下的振动响应,表明了长径比的增加会导致弹体刚度降低。刘波[8]通过对实测侵彻加速度信号的处理,指出信号功率峰值频率与模态分析固有频率有较好的吻合度。以上学者研究表明大长径比弹体结构的振动响应特性是研究其动态响应、装药及引信安定性的关键问题。
综上所述,本文中针对大长径比弹体在极端载荷下的结构优化设计及振动响应特性的问题,以典型SDB结构为具体研究对象,开展其在侵彻混凝土靶时的结构强度、稳定性及振动响应特性研究,明确其在不同打击工况下极限安全壁厚设计、抗弯破坏临界倾角及攻角的控制要求,讨论不同弹目交汇条件及无量纲壁厚对结构弯曲变形的影响规律,得到弹体结构参数、着靶状态参数、材料强度之间的多参数约束控制条件,给出满足结构稳定的设计要求和工况范围,并通过有限元模态分析及谐响应分析获取结构固有频率及模态振型,为大长径比弹的结构优化设计、能力校核及服役作战参数选择提供理论依据和合理建议。
1 SDB侵彻混凝土结构强度及稳定性研究
典型SDB弹体结构及简化示意如图1所示。主要由侵彻壳体及装药、引信装置、GPS/INS制导装置3部分构成。全弹长为1.828 m,弹径0.152 4 m,长径比约为12,忽略装药及内部结构的质量分布和承载能力。无量纲壁厚为0.10~0.12、CRH近似为4.5、壳体质量113 kg、炸药质量22.7 kg、装填比20%、着靶速度一般为200~600 m/s,取弹体材料破坏强度σcr=1 650 MPa,屈服强度σY=1 500 MPa。

图1 SDB结构示意图(mm)Fig.1 Schematic diagram of SDB structure
1.1 SDB结构强度分析
SDB在侵彻混凝土靶时,主要会出现2类结构强度及完整性问题,一是在垂直侵彻时的轴向压溃或者拉伸破坏;二是倾角或攻角侵彻时的弯曲破裂及折断。针对弹体的2种破坏模式,本节将分析确定SDB在不同工况下的弹体极限壁厚以及抗弯极限姿态。
1.1.1正侵彻抗压极限壁厚分析
本文中的研究均不考虑弹体在高速侵彻下的头部侵蚀及质量损失。在垂直正侵彻条件下,等壁厚弹体结构的危险截面通常位于弧柱交界面处[2]。Forrestal等[9]给出的弹体正侵彻混凝土时的轴向阻力模型,结合危险截面的强度要求,陈小伟等[1]获得了弹体结构保守抗压无量纲极限壁厚公式:

(1)


(2)
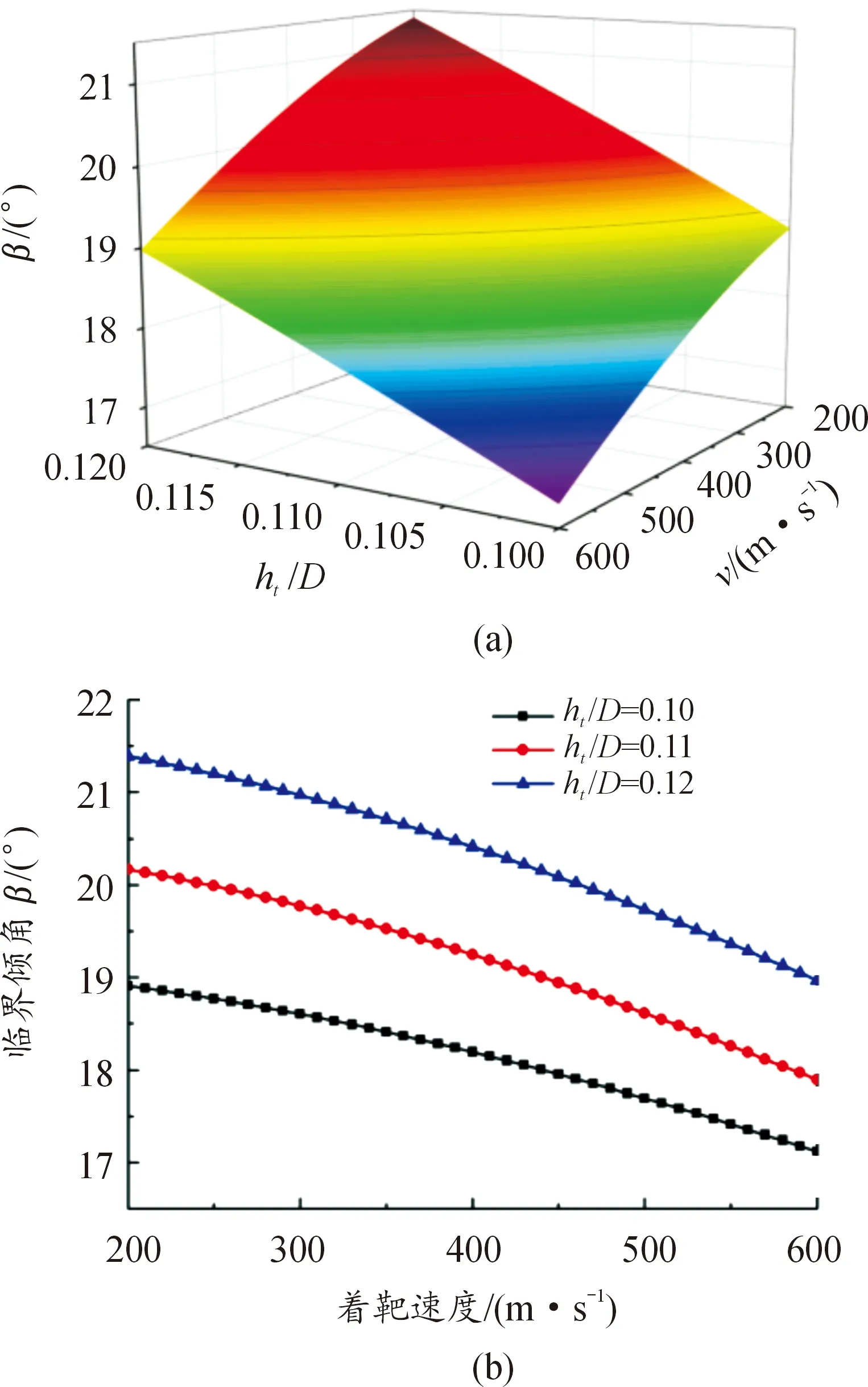
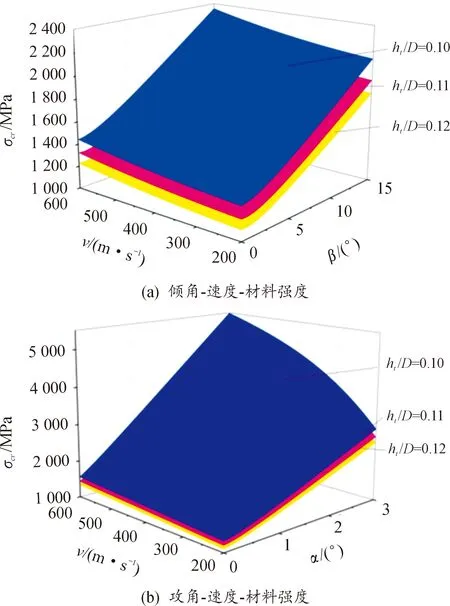
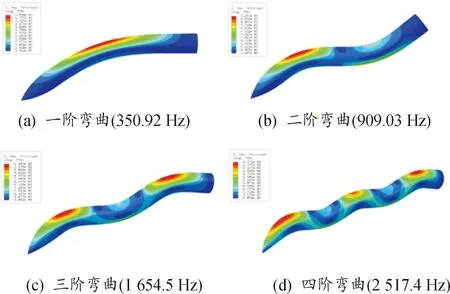
图2(a)给出了SDB以200~600 m/s着靶速度正侵彻30~50 MPa混凝土靶时的极限壁厚。随着弹体着靶速度、混凝土强度增加,弹体所受冲击过载增大,弹体极限壁厚也随之增大。以图2(b)中50 MPa强度混凝土为例,对于v0<300 m/s的低速撞击,ht/D>0.085;对于300 m/s≤v0<400 m/s的音速撞击,ht/D>0.088;而针对400 m/s 1.1.2非正侵彻抗弯临界倾角分析 在实战中,弹体侵彻目标时常带有倾角(定义为弹体轴线和靶体表面法向的夹角)和攻角(定义为弹体速度方向与弹身轴线的夹角),二者会导致弹体头部受到不对称载荷作用,结合自由面效应的影响,弹体头部会受到与弹体轴线垂直方向的横向载荷,进而在弹体截面产生弯曲应力。为避免弹体结构发生弯曲破坏,倾角及攻角存在上限,因此需确定SDB在非正侵彻时的倾角及攻角安全范围。 本小节分析SDB弹体以初始速度v0、初始攻角α为零条件下,侵彻半无限混凝土靶的抗弯破坏临界倾角β。 倾角侵彻半无限混凝土靶如图3所示。 图2 极限壁厚同着靶速度及混凝土强度的变化规律Fig.2 The relationship between dimensionless limit thickness of projectile、target velocity and concrete strength 图3 倾角侵彻半无限混凝土靶示意图Fig.3 Schematic diagram of the projectile into the semi-infinite concrete target with oblique angles 陈小伟[10]指出弹体以倾角β斜侵彻目标时最大横向载荷发生在撞击开坑段中间,呈现先增大后减小的变化趋势,这里采用其给出的平均侧向作用力表达式 Fy= (1/2)Fmaxsinβ= (1/2)(πD2/4)(Sfc+N*ρv02)sinβ x/D>k (3) M.J.Forrestal等[11]给出了此条件下的轴向载荷表达式 (4) X.W.Chen[1]基于自由梁模型分析了弹体在横向过载下的结构动态响应,并结合危险截面的强度要求给出了临界倾角的计算式 (5) 式(5)中:d为弹体内径,由式(5)可知,在头部形状、弹靶材料及长径比确定的情况下,临界倾角主要受无量纲壁厚及着靶速度控制。图4(a)中曲面给出了不同无量纲壁厚(0.10~0.12)弹体以200~600 m/s的着靶速度侵彻40 MPa混凝土时的临界倾角。结合图4(b)可以看出,随着着靶速度的增大,临界倾角减小。以无量纲壁厚0.12弹体为例,着靶速度由200 m/s提升至600 m/s,临界倾角由21.4°降低为19.0°。随着弹体壁厚增加,临界安全倾角增大,相同着靶速度下,弹体无量纲壁厚增大10%,临界倾角增大约5%~8%。保守估计,针对600 m/s的着靶速度上限,无量纲壁厚分别为0.10、0.11、0.12弹体结构允许的最大倾角分别为17°、18°以及19°。整体来看,当倾角超过20°时,弹体易发生弯曲破坏。对于中低速撞击,可以根据图4确定不同工况下倾角的安全范围。同时依据式(5),表1给出SDB在不同典型倾角以及着靶速度下的极限无量纲壁厚,当倾角以及着靶速度增大时,需相应增加壳体厚度。 本小节中将确定SDB弹体以初始速度v0、初始倾角β为零条件下侵彻半无限混凝土靶的临界攻角α。攻角侵彻半限混凝土靶如图5所示。 图4 临界倾角同着靶速度、无量纲壁厚的变化规律Fig.4 The relationship between critical oblique angles、 dimensionles thicknessof projectile and targeting velocity 表1 不同倾角及着靶速度下的极限无量纲壁厚Table 1 Limit dimensionless thickness of projectile at different oblique angles and targeting velocity 图5 攻角侵彻半无限混凝土靶示意图Fig.5 Schematic diagram of the projectile into the semi-infinite concrete target with attacking angles 王成华等[12]指出在小攻角范围内,轴向载荷几乎不随攻角变化,并给出了弹体在初始倾角β为零条件下,以攻角α侵彻半无限混凝土靶时所受横向过载的半经验表达式 (6) K=3.93×(0.817 8+4.919×10-2ψ) (7) 参考X.W.Chen[1]的分析方法,推导可得弹体临界安全攻角为 (8) 图6(a)中曲面给出了不同无量纲壁厚(0.10-0.12)弹体以200~600 m/s的着靶速度侵彻40 MPa混凝土时的临界攻角。 图6 临界攻角同着靶速度、无量纲壁厚变化规律Fig.6 The relationship between critical attacking angles、 dimensionless thickness of projectile and targeting velocity 结合图6(b)可知,随着着靶速度的增大,临界攻角减小,且变化较为敏感,当无量纲壁厚为0.12弹体的着靶速度由200 m/s提升至400 m/s、600 m/s时,临近攻角由2.70°降低至1.50°和1.24°。随着弹体壁厚的增加,临界攻角增大,相同着靶速度下无量纲壁厚增加10%,临界攻角增大约10%。依据式(8),表2同时给出SDB在不同典型攻角以及着靶速度下的极限无量纲壁厚。 表2 不同攻角以及着靶速度下的最小无量纲壁厚 大长径比弹体非正撞击目标时,头部会受到轴向载荷与横向载荷的耦合作用,弹体在此复杂受载环境下极易出现弯曲变形的结构失稳现象。SDB弹体在非正侵彻混凝土靶时的结构稳定性问题,归结为任一截面在轴向过载和弯矩作用下是否到达屈服,产生塑形弯曲变形。皮爱国等[14]给出了理想弹塑性材料弹体截面同时承受轴力N和弯矩载荷M时的耦合屈服函数Φ及结构稳定条件 目前市面上销售的樟脑丸分天然和人工合成两种。天然樟脑丸主要是从樟树的枝叶中提取加工而成,呈无色或白色晶体状,无毒,气味清香;而合成樟脑丸大多由对二氯苯为原料制成,气味刺鼻,有一定毒性,放置不当或放得太多会使人产生头晕、打喷嚏、皮肤过敏等症状。 (9) N=Fx(1-x/L) (10) M=Fy(x-2x2/L+x3/L2) (11) 式(9)中,NY和MY分别截面为单独受压及受弯的屈服极限。式(10)和(11)中,x为截面到弹头的距离。对于等壁厚圆筒截面有 (12) (13) 1.2.1倾角侵彻下的弹体屈服变形 图7—图9分别给出了控制变量下,不同着靶速度、倾角以及无量纲壁厚所对应弹体无量纲屈服函数的分布规律,曲线极值对应弹体的危险截面,从图9中可以看出危险截面位于弧柱交界附近到距离头部L/3之间。 图7给出了无量纲壁厚为0.10的SDB弹体以10°倾角、0°攻角侵彻40 MPa混凝土时,屈服函数分布规律及随着靶速度变化规律。随着着靶速度的增大,各截面屈服函数值增大,且危险截面的函数值均已大于0,弹体发生塑性弯曲变形。 图7 不同着靶速度下屈服函数分布Fig.7 Dimensionless yield function distribution at different target velocities 图8给出了无量纲壁厚为0.10的SDB弹体以300 m/s着靶速度、0°攻角侵彻40 MPa混凝土时,屈服函数分布规律及同倾角的变化规律。随着倾角的增大,截面屈服函数的值也随之增大,危险截面随倾角的增加由弧柱交界处向尾部移动。在0°≤β≤5°范围内时,弹体屈服函数变化随倾角变化不明显,呈近似线性分布关系,危险截面函数小于0;当β≥10°时,屈服函数对入射角度的变化开始变得敏感,屈服函数曲线由近似直线向波峰状转化,且危险截面的屈服函数值已经大于0,结构产生弯曲塑性变形;随着倾角进一步增大,弹体弯曲已不可避免;在5°~10°间,存在结构稳定的临界状态。 图8 不同倾角下屈服函数分布Fig.8 Distribution of dimensionless yield functions at different oblique angles 图9给出了SDB弹体以300 m/s着靶速度、10°倾角、0°攻角侵彻40 MPa混凝土时,屈服函数分布规律及同无量纲壁厚的变化规律。从图9中可以看出随着弹体壁厚的增加,屈服函数值减小;当无量纲壁厚增大至0.12时,函数极值小于0,结构具有较好的抗弯变形能力,因此适当增加弹体的壁厚可以有效提高结构的稳定性。 图9 不同无量纲壁厚下屈服函数分布Fig.9 Distribution of dimensionless yield function at different dimensionless thicknesses of projectile 1.2.2攻角侵彻下的弹体屈服变形 图10—图12分别给出了控制变量条件下,不同速度、攻角以及无量纲壁厚所对应弹体无量纲屈服函数的分布规律,危险截面同样位于弧柱交界处到距离头部L/3之间。 图10给出了无量纲壁厚为0.10的SDB弹体以0°倾角、1°攻角侵彻40 MPa混凝土时,屈服函数分布规律及同着靶速度之间的变化规律。与斜侵彻规律相似,随着初始着靶速度的增大,任一截面屈服函数值增大,当速度由300 m/s提升至400 m/s、500 m/s,函数极值分别由0.24增大至0.32和0.43。可以看出由于攻角的存在,使得弹体结构更易因速度的提升而变得不稳定,在提升速度的同时,需要严格控制攻角姿态。 图10 不同着靶速度下屈服函数分布Fig.10 Dimensionless yield function distribution at different target velocities 图11给出了无量纲壁厚为0.10的SDB弹体以300 m/s着靶速度、0°倾角侵彻40 MPa混凝土时,屈服函数分布规律及同攻角变化的规律。弹体在承受巨大轴向过载情况下,屈服函数对攻角的细微变化显得尤为敏感,极小攻角的增加都会引起屈服函数值极大的增幅。攻角为1°时,攻角引起的横向过载较小,屈服函数值较低,变化较为平缓,但危险截面的函数值已经大于0,弹体已经可能发生弯曲变形。在2°攻角时,屈服曲线变化明显,函数值极值为0.83。在3°攻角时,曲线更为陡峭,最大函数值已经高达1.43,远远大于安全值,对弹体结构的稳定性产生极大的威胁。 图11 不同攻角下屈服函数分布Fig.11 Distribution of dimensionless yield functions at different attacking angles 图12给出了SDB弹体以300 m/s的着靶速度,0°倾角、1°攻角侵彻40 MPa混凝土时,屈服函数分布规律及同无量纲壁厚的变化规律,随着壁厚的增加,屈服函数值减小。 图12 不同无量纲壁厚下屈服函数分布Fig.12 Distribution of dimensionless yield function at different dimensionless thicknesses of projectile 由1.2.1和1.2.2节的分析对比可以得到,SDB非正侵彻时,危险截面位于弧柱交界处到距离头部约L/3之间,并随着倾角和攻角增大逐渐向弹体尾部移动,可以考虑在附近位置进行局部壳体加厚或者环向加筋处理。着靶姿态是影响弹体结构稳定性的重要因素,攻角的存在会明显加剧速度增大对弹体结构稳定产生的恶劣影响,在相同速度下攻角对弹体结构弯曲的影响更为显著,这与刘坚成等[15]的实验结论一致。图13为文献[15]中弹体非正侵彻反弹道实验的弯曲变形情况。弹体结构参数与实验工况见表3、表4[15]。 从弹体变形结果可以看出,2类非正侵彻情况下弹体弯曲变形位置大致均位于弧柱交界处到距离头部约L/3之间,与上述理论分析吻合。在仅倾角侵彻下,弹体弯曲变形并不显著,随着倾角增加,15°倾角和10°倾角较0°倾角时弯曲略大,但并不明显。在仅攻角侵彻时,弹体弯曲变形更为显著,小幅度的攻角即会引起剧烈的结构响应。实验结果表明3°攻角侵彻后的弹体端部挠度大于10°倾角的侵彻结果。 图13 弹体结构响应情况[15]Fig.13 Structural response of projectile 表3 弹体结构参数Table 3 Parameters of experiment projectile 1.2.3弹体结构稳定多参数控制约束条件 1.2.1和1.2.2节分析了着靶速度、着靶姿态以及无量纲壁厚对弹体结构稳定性的影响规律,本节将从弹体结构参数设计及控制弹目交汇条件角度出发,给出不同工况下保证弹体结构稳定的设计及控制要求。根据耦合屈服函数可以将控制弹体结构稳定的参数特征分为2类,一类是弹体的着靶状态,包括倾角、攻角和着靶速度,这主要决定了弹体所受的外载特征;另一类是弹体的结构参数,包括无量纲壁厚和长径比,决定了弹体结构的响应特征。根据屈服函数可以确定不同弹目交汇条件下危险截面所在位置,利用屈服条件对危险截面进行校核控制,进而得到在保证弹体结构稳定条件下,着靶状态、弹体结构及材料屈服强度之间的约束控制条件。 以侵彻40 MPa强度混凝土为例,图14(a)给出了长径比为12、无量纲壁厚为0.10的弹体在攻角为零,0°≤β≤15°、200 m/s≤v≤600 m/s范围内、弹体着靶速度、倾角和弹体材料强度之间的控制约束条件。图14(b)给出在倾角为零,0°≤α≤3°、200 m/s≤v≤600 m/s范围内为弹体着靶速度、攻角和弹体材料强度之间的控制约束条件。图14中曲面代表了弹体危险截面不发生弯曲塑性变形的临界状态,在对应的着靶状态下,位于曲面下方的状态表示弹体已经进入屈服,曲面上方即为安全,不会发生弯曲变形。由图14可知,随着倾角、攻角以及着靶速度的增大,对材料强度要求也随之增高。 对比可知,相较倾角变化带来的影响,攻角变化带来的影响更为显著。以300 m/s着靶速度为例,倾角由0°增大至8°时,弹体材料屈服强度需要由1 300 MPa提高至1 680 MPa,而攻角由0°增大至1°时,材料强度需要由1 300 MPa提高至 2 100 MPa。对于本文中屈服强度为1 500 MPa的弹体材料,允许的最大倾角为7°,最大攻角只有0.8°。在攻角小于1°时,材料屈服强度对速度变化并不敏感,但攻角的进一步增大会明显加剧速度变化带来的影响。当攻角为1°,着靶速度由200 m/s增大至600 m/s时,材料强度需要由1 625 MPa提高至2 400 MPa,常规弹体材料已不能满足强度需求;而当攻角为2°时,相应的材料强度需要由1 950 MPa提高至3 500 MPa。依据图14,可以依据弹体材料强度,控制着靶姿态及着靶速度,同时可以根据着靶状态选取弹体材料强度。 在无法有效控制着靶姿态的情况下,需要依据着靶姿态及速度反向设计优化弹体结构。图15分别给出了弹体以10°倾角和1°攻角、400 m/s着靶速度侵彻40 MPa混凝土靶时,弹体长径比、无量纲壁厚和材料屈服强度之间需要满足的条件,曲面上任意一点为弹体稳定的临界状态。从图中可以直观看出,无量纲壁厚以及长径比都明显影响着弹体结构的稳定性,随着长径比的增大以及无量纲壁厚的降低,对材料强度的要求显著提高。 图15 耦合屈服条件下无量纲壁厚、长径比和 材料强度之间的关系(v=400 m/s)Fig.15 Relationship between dimensionless thickness of projectile、length-diameter ratio and projectile material strength(v=400 m/s) 由图15可知,当倾角为10°,弹体材料强度1 566 MPa时,无量纲壁厚由0.10增大至0.11,长径比可以由8提高至9.2;无量纲壁厚增大至0.12时,长径比可以进一步提高至10.4。以无量纲壁厚0.11弹体为例,将长径比由8提升至12,相应材料强度需要由1 505 MPa增强至1 735 MPa;当攻角为1°,材料强度为1 698 MPa时,无量纲壁厚由0.10增大至0.11、0.12时,长径比可以分别由8提高至9.1和10.3。将无量纲壁厚0.11弹体长径比由8提升至12时,材料强度需要由1 669 MPa提高至1 919 MPa。依据图15,在材料强度受限时,适当增大结构的无量纲壁厚可以在不明显影响装填比的情况下可靠提高结构长径比,提升侵彻能力。 为保证弹体结构稳定的作战要求,图16分别给出在不同无量纲壁厚下,材料屈服强度与着靶速度及着靶姿态(倾角、攻角)的关系。图17分别给出了在不同倾角及攻角下材料屈服强度同无量纲壁厚及长径比之间的关系。根据图16、图17,可以实现弹体结构、材料性能与侵彻条件的相匹配,实现节约成本和高效侵彻的作战目标。 图16 不同无量纲壁厚下着靶姿态、着靶速度和 材料强度之间的关系(L/D=12)Fig.16 The relationship between yield strength of projectile、 targetposture and target velocity under different dimensionless thicknesses of projectile (L/D=12) SDB在撞击靶板瞬间,会受到冲击载荷作用产生应力波效应,诱导弹体结构产生振动响应,鉴于SDB大长径比结构特点,振动响应在实际服役过程中会对弹体整体结构响应、装药及引信安定性产生巨大影响,需对SDB结构的波动效应和振动响应特性展开研究。 刘波[8]基于波动方程给出弹体轴向振动固有频率的理论模型,并通过对实测加速度信号分析验证了方法的有效性。本节利用Abaqus有限元分析软件对全弹结构模型进行模态分析,结构参数见图1,这里忽略尾部制导装置以贴近实际侵彻过程。材料密度7 800 kg/m3,弹性模量210 GPa,泊松比为0.28。设置弹体为无约束自由状态。图18为弹体1/2 有限元模型。模态分析前40阶结果如表5所示。 图18 SDB有限元模型Fig.18 Finite element model of SDB 表5 模态分析前40阶结果Table 5 Modal analysis results 由表5可知,弹体的前六阶模态基本为零,分别对应弹体的刚体平动、转动模态振型,之后主要是拉压、径向褶皱和弯曲振型。大部分振型成对出现,对应频率几乎相等,只是在空间方向上的分布不同。图19、图20分别为弹体轴向振动及弯曲振动前四阶固有频率及模态振型,弯曲振动的波节数随模态阶数的提高而增大。 为分析弹体结构在特定频率简谐周期激励下的稳态响应特征,获得弹体在侵彻阻力作用下达到共振条件的频率值,利用图18有限元模型对弹体结构进行谐响应分析,激励范围为0~6 500 Hz。主要考虑弹体的轴向振动模式,为模拟侵彻载荷,施加轴向载荷于弹体头部外表面,同时为满足静定条件,固定弹尖。图21给出了弹体特征节点的频响曲线,特征节点分别取在弹体前部弧柱交界处、弹体中部及尾部。 图19 弹体轴向振动前四阶振型Fig.19 The first four-order axial vibration mode of the projectile 图20 弹体弯曲振动前四阶振型Fig.20 The first four-order bending vibration mode of the projectile 图21 弹体各位置轴向加速度过载-频率曲线Fig.21 Axial acceleration overload-frequency curve at different position of the projectile 表6为模态分析与谐响应分析结果与简化模型理论值的比较。 表6 模态分析与谐响应分析结果与理论模型对比情况 结合表6及图21可知,3个位置的共振频率相近,分别在1 887、3 730、5 550 Hz附近加速度过载达到峰值,发生共振现象,并且分别对应弹体轴向振动一阶、二阶、三阶固有频率,模态分析结果与谐响应结果有较好的吻合性。结果显示不同模态振型在弹体不同位置的参与程度不同,在弹体前部,主要为二阶振动模态;在弹体中部,主要受一阶和三阶振动模态振型主导;在弹体尾部,一阶和二阶振动模态振型参与较多,此差异是由于应力波在弹体中的传播特性及弹体结构特点所导致的,反映了应力波在弹体中的波动特性。在弹体结构设计、引信安装位置选择及实测过载数据的处理上[16],应该对其充分考虑。 通过对大长径比结构弹体侵彻混凝土靶板时的结构强度、稳定性问题及振动响应特性研究,得出主要结论如下: 1) SDB在200~600 m/s的中低速范围内正侵彻30~50 MPa强度混凝土,极限无量纲壁厚在0.095以上是较为保守的设计;非正侵彻时安全倾角范围不超过20°,安全攻角范围不超过3°;随着着靶速度的增大以及无量纲壁厚的减小,临界倾角和攻角降低。 2) 着靶姿态是影响大长径比弹体结构稳定性的关键因素,且对攻角的敏感性远大于倾角,攻角的存在会明显加剧着靶速度增大对弹体结构稳定产生的影响,适当增大无量纲壁厚是提升结构稳定性的有效手段。 3) 基于弹体结构稳定性多参数控制约束条件,得到了弹体结构参数、着靶状态参数以及弹体材料强度之间的耦合影响规律。针对本文中的SDB以300 m/s速度侵彻40 MPa混凝土,在保证结构稳定的要求下,允许的最大倾角约为7.0°~9.0°,最大攻角约为0.8°~1.0°。 4) 通过模态分析得到SDB前40阶固有频率及轴向和弯曲模态前四阶振型,由谐响应分析获得了SDB轴向振动频响曲线和共振频率,二者结果吻合较好,与理论简化模型的偏差在5%~7%左右,揭示了弹体中的应力波传播效应和结构振动响应特征。





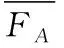
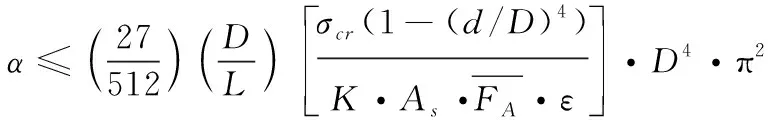


1.2 弹体非正侵彻结构稳定性分析
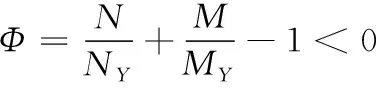











2 大长径比弹体结构振动响应特性分析
2.1 模态分析


2.2 谐响应分析



3 结论

