离散数学应用型本科课程建设探索

李伟伟 李保田 寻 杨 杨菲菲 陈健健

1.山东青年政治学院信息工程学院 山东济南 250103;2.山东省高等学校智能信息控制新技术研发中心 山东济南 250103;3.山东省高校智慧康养大数据工程与泛在计算特色实验室 山东济南 250103

离散数学是计算机类专业的基础课程,内容抽象,理论性强[1]。通过离散数学的学习学生可以掌握数理逻辑、集合论和图论的基本概念与基本理论[2],了解这些内容与计算机学科的其他课程的关系。学生的抽象思维和缜密概括能力会得到明显提高[3],为数据结构、操作系统、编译原理、模糊数学等后续课程的学习打下良好基础[4]。离散数学在实际生产生活中应用也非常广泛,很多理论是源于实践,又能指导实践,也是应用型本科建设的重要课程。

1 课程目标制定

离散数学作为应用型本科建设的重要课程,在课程目标制定时要对标计算机科学与技术应用型专业制定的专业目标,对专业目标予以支撑。本应用型课程目标对应用型专业目标的支持如表1:

表1 离散数学课程对应用型专业目标支撑度分析

2 教学内容与章节安排

本课程内容主要包括数理逻辑、集合论、图论等,为学习数据结构、数据库等计算机专业课程打下坚实的基础。在传授知识的同时特别注意培养学生把所学知识应用到实际问题中的能力。教学内容更加重视综合应用能力的培养,授课案例和自主学习内容更贴合我校计算机科学与技术专业确立的“计算机+康养”的发展目标;注重引入职业证书考试、科创竞赛内容。各章节的安排与学时分配如表2所示:

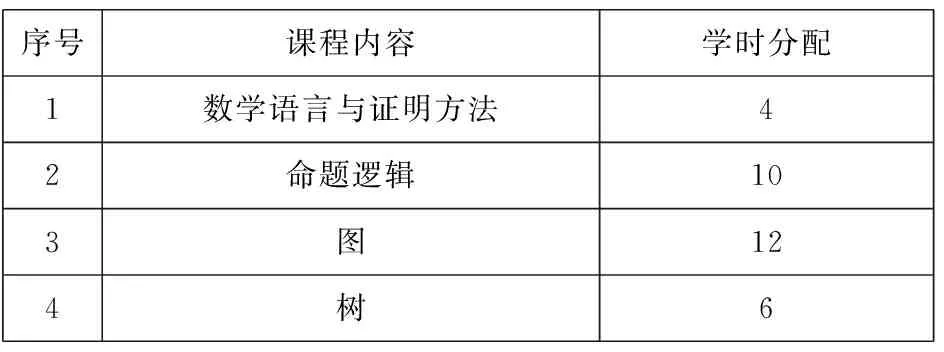
表2 课程学时分配

对标康养文旅,增加相关应用案例。在各个章节增加对标康养文旅的案例,例如在欧拉图部分增加哥尼斯堡七桥问题,在哈密顿图部分增加周游世界问题,在最短路径部分增加旅游路线规划问题。

例1:在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图1)。是否可能从这四块陆地中任一起出发,恰好通过每座桥一次,再回到起点?

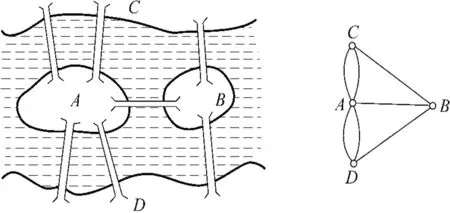
图1 哥尼斯堡七桥问题

例2:周游世界问题在1859年被英国数学家哈密顿提出:二十个城市用一个正十二面体的二十个顶点代表,从一个城市出发,沿着棱经过每个城市恰好一次,怎样才能最后返回到出发点?如图2:

图2 周游世界问题

例3:一名青年学生生活在城市A,准备假期到郊区景点B,C,D去旅游,然后回到A。图3给出了A、B、C、D的位置及它们之间的距离(千米)。该青年如何走行程最短?

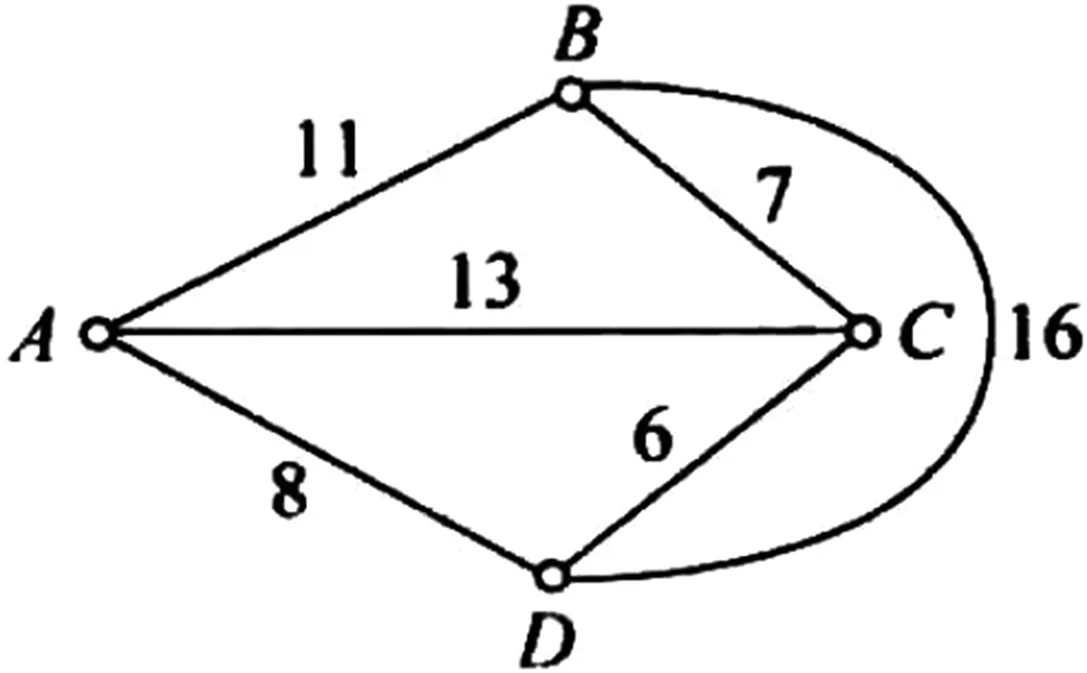
图3 景点路线及距离

3 考核方式改革

在OBE理念指导下进行过程性考核和期末测试,使之能对课程目标形成有效支撑和全面覆盖。改革重点如下:

(1)在OBE理念指导下进行平时测试、期末测试、实验课后思考题的设计,使之能对课程目标形成有效支撑和全面覆盖。

(2)突出离散数学课程在计算机各专业课中的应用能力的考查,重点考查利用离散数学知识解决计算机中应用问题的能力。

(3)增加对标计算机各专业课程的案例和习题;增加对标康养文旅的应用型案例和习题。

(4)课程考核结束后,采用OBE理念下的目标达成度分析方法,全面分析学生表现对课程目标和毕业要求指标点的达成情况。对于达成度不理想的课程目标,提出针对性的改革措施,形成持续改进的闭环结构。

本课程具体考核方式如下:

考核成绩构成:总成绩=平时50%+期末50%

平时过程性考核成绩=课堂考勤(10%)+课堂表现(50%)+课程作业(20%)+在线测试(20%)

在得出上述各项原始成绩之后,在OBE理念指导下,计算学生成绩对各教学目标和各二级指标点的达成度。具体计算方式如下:

课程评价依据。根据课程目标,确定课程目标权重以及各项考核所占比例。各评价依据权重如表3所示。

表3 各评价依据权重

计算课程目标达成度和毕业要求指标点达成度,具体计算方法如表4所示:

表4 课程目标达成评价及指标点达成值

Bi:课程目标i的得分。计算方法:Bi=∑Tj×wj。其中,Tj表示分项达成值,wj表示分项权重。Tj的计算方法为:

Wi:课程目标i的达成度权重系数,该系数是由各评价依据成绩在总评成绩中的占比决定的。

OBi:课程目标i的达成度计算值。计算方法:

注:课程目标和指标点一一对应,指标点达成值等于课程目标达成值。

4 课程教学团队建设

本教学团队共3人,博士2人,硕士1人,教授1人,副教授2人,青年教学能手1人。年龄、职称结构合理。近五年,团队成员发表学术论文10余篇,主持或参与省级教改项目、校级科研项目等多个项目;获校级教学成果奖二等奖两项;3名教师均具有丰富的企业实践锻炼工作经验;团队教师参加教学创新大赛并获奖,目前的教学团队基本可以满足本课程的教学需求,并聘请教育信息技术学专家1名,给予教学方法的指导。

5 未来建设重点

应用型本科课程的建设需要持续建设,不断改进,未来建设重点如下:

(1)企业实践。鼓励团队教师参加企业挂职锻炼活动,深入了解软件企业的开发过程,增强教师的实际开发水平。

(2)教学研究。鼓励团队教师积极申报各类教学研究项目,提高团队教师的教学研究能力和团队合作能力。

(3)校企合作。鼓励团队教师与合作企业进行对接,在企业工程师的指导下开展教学设计和课程实验开发。同时,积极与企业联系,承担对外的软件开发与技术咨询横向课题。

结语

应用驱动创新,对标计算机科学与技术应用专业建设目标,本课程对应用型专业建设提供了有力支撑。通过目标制定、内容调整、考核方式改革、教学团队建设,把离散数学课程建设成为应用型课程。通过本课程的学习,学生的应用能力得到大幅度提升,因学有所用,学生学习积极性也得到大幅度提高。