船舶有限元模型舱室识别方法
张志康,刘 戈,陈乐昆,李 闯,张思航,孙明宇
(1.中国船舶及海洋工程设计研究院,上海 200011;2.中国船舶集团有限公司系统工程研究院,北京 100000)
0 引言
有限元分析是船舶结构设计中非常重要的校核方法,一般包括舱段有限元分析和全船有限元分析。在强度分析时,舱室内部水压力载荷的施加和构件腐蚀扣除的确定均与舱室相关,因此舱室定义是必不可少的环节。
手动搜索舱室空间的边界单元,不仅费时费力,效率低下,而且还容易出错。尤其是近年来《散货船和油船共同结构规范》(HCSR)生效后,规范对散货船和油船的舱段校核范围要求由中间货舱扩展到全船各货舱[1],不仅工作量加重,而且船首和船尾区域的线型变化剧烈,给舱室定义增加了难度。此外,对于集装箱船、客滚船和豪华邮轮等需进行全船有限元计算的船型,每条船需定义的各类大小舱室多达上百个,非常考验设计人员的体力与耐心。因此,急需实用、高效和智能的舱室自动识别算法和程序,以期能够缩短操作时间,提升设计人员的效率。
针对此类舱室空间边界自动识别的问题,国内外学者也进行了不少研究。单威俊等[2~4]基于有限元模型,提出“切分拼接法”实现舱室边界单元的识别,并基于Patran 开发自动化程序,该程序已经纳入CCS 的HSCR 规范校核软件体系中,但识别过程仍需用户人为干预,且对船首、船尾等曲面较复杂的区域,识别精度还有待提高。章志兵等[5]提出一种基于CAD 模型的舱室识别算法,并在NX 平台上以C++语言编程实现,算法自动化与智能化程度高,有助于舱室快速建模。章志兵等[6]通过设计网格拓扑关系和分析舱室的几何特征,基于半边半面结构,提出了半面封闭空间概念,并利用半面扩展算法,实现了CAE 模型舱室的自动识别,但仅限于封闭舱室,且算法相对复杂。此外,法国船级社的商业软件Veristar Hull 可以对有限元网格进行舱室搜索,但仅限于水密舱室,内在算法也不得而知。
本文基于拓扑学原理和船舶舱室特征,提出一种基于CAE 的船舶舱室识别算法“无自由边法”,该算法适用于多种船型及任意复杂的舱室,且改进算法可适用于非封闭舱室。在此基础上开发出自动化程序,经过实船测试验证,能够大幅提高舱室定义效率,具有工程应用价值。
1 舱室识别
船舶舱室最典型的特点为大多是水密舱室,因此本研究以该特点为突破点,从识别有限元三维封闭空间入手,提出一种“无自由边法”以实现船舶水密舱室的识别,并针对非水密舱室对算法进行改进与优化,以提高算法的适用性。
1.1 原 理
首先,根据某舱室的空间位置搜索该范围内的所有单元(Elem),统计这些单元的边(Edge)及其数量,其中数量等于1 的一定是自由边(Free edge)。根据该原则筛选出所有自由边,然后将其所属单元剔除出集合,接着重新统计边与数量,以此不断循环往复,直到没有自由边。最终,剩下的单元便形成封闭的三维空间,组成船舶舱室的搜索目标边界。
现有研究的搜索方法大多属于“加法”,而本文提出的算法则采用的是“减法”思想。
1.2 实现过程
舱室识别的流程如图1 所示。

图1 舱室识别流程Fig.1 Recognition process of ship compartment
步骤1根据船舶舱室边界的定义,获取该长方体空间内的所有单元Elem 和及其Edge 元素。
步骤2建立有限元模型的拓扑关系,并创建单元和边的数据结构储存拓扑关系。
步骤3寻找唯一存在的Edge;若不存在,则结束。
步骤4识别该Edge 所属的单元,将其从表示封闭空间的单元数组中剔除,并更新边的数据储存Hash 表。
步骤5将结果作为新的输入,回到步骤3,递归执行舱室识别过程。
1.3 建立拓扑关系
船舶舱室是由一组单元组成的封闭空间区域,各个单元之间由单元边相互联系。为实现本文的算法,需建立的拓扑关系:单元与边的组合关系,边与边的重合关系。
将单元边定义为从起点Start node 指向终点End node 的有向边(Start node,End node),其中起点的编号一定比终点的编号小。
如图2 所示,单元Elem_1 包含有向边(1,2),(2,3),(3,4)和(1,4);单元Elem_2 包含有向边(3,4),(4,6),(3,5)和(5,6)。它们存在共同边(3,4),该边的数量为2,其余均为1。

图2 拓扑关系示意Fig.2 Topological relation
将Elem 和其包含的有向边储存在二维数组中。另外以有向边的名称作为Key,数量作为Value,使用Hash 表进行储存。
1.4 算法介绍
“无自由边法”算法用于搜索三维模型中由单元构成的封闭空间。
首先,确定搜索范围。舱室定义数据包括了舱室名称和x,y和z方向的范围值。因此,对于单个舱室的搜索范围{Elem_i},它包含的单元坐标应满足式(1)~式(3)。
建立该范围内的拓扑关系,创建包含Elem 和有向边的二维数组,及储存有向边和数量的Hash 表。
查询Hash 表中Value 等于1 的Key,则该有向边即为自由边。通过二维数组获得该自由边所属的Elem,一方面将其从{Elem_i}内剔除,另一方面记录它包含的其他有向边,再次查询Hash 表,各有向边对应的Value 减一。
把更新后的二维数组和Hash 表作为新的输入,进行递归运算,直至无法找到自由边,则{Elem_i}内包含的单元即为该舱室的边界。运行过程如图3 所示。

图3 “无自由边法”示意Fig.3 No free edge algorithm
2 算法改进
“无自由边法”本质是搜索有限元网格中的封闭空间。为了扩大算法的适用性,满足工程实际应用的需求,针对非封闭空间的识别问题,对本文的算法进行改进和优化。
2.1 舱室边界带有小孔
在实际的舱室定义过程中,常常碰到有限元模型中水密舱室边界有小孔、不封闭的情况,此时类似的舱室搜索算法都会失效,而手动去寻找缺失的单元和修补也会非常耗时。
导致此问题的原因有2 种:一种是由于建模人员在建模过程中的粗心,不小心遗漏了一些网格单元;另一种是考虑了水密舱室上的人孔。
针对有限元模型中水密舱室边界上缺失多个且“独立”单元的情况,对本文提出的算法进行优化。大致的原理:不以有向边的数量来判断是否为自由边,而是以单元节点Node 的数量作为依据,即搜索范围内Node 数量≤2 的,其所属有向边即为自由边。
基于该改进算法,便可准确识别此类带小孔的舱室。
2.2 货舱大开口
对于散货船和集装箱船这类船型,货舱均带有大开口,对此现有的舱室搜索算法均不适用。
文献[5]中提出手动创建舱口盖进行封口的预处理方法,虽然能将此类大开口舱室转换为“封闭舱室”,但考虑到货舱的数量较多,因此处理起来还是过于繁琐。
本文借鉴此预处理的思想,提出给此类货舱加一个虚拟“货舱盖”的改进算法。具体实现方法:在自由边的判断过程中,若有向边的2 个节点都在“货舱盖”的高度方向上,则该有向边必定不是自由边。该改进算法可由程序自动实现,避免了人工预处理的工作,有利于提高舱室识别效率。
3 应用实例
FEMAP 是一款先进的有限元分析软件,提供完全开放的二次开发接口,支持各种通用语言,非常适用于CAE 的二次开发[7]。基于该软件,采用VB.NET 语言和WinForm 客户端开发技术,实现本文提出的舱室识别算法。
对某15000TEU 集装箱船实船项目的全船有限元模型进行测试。全船有限元模型如图4 所示,共计约62 万个单元,需定义的舱室总计110 个。
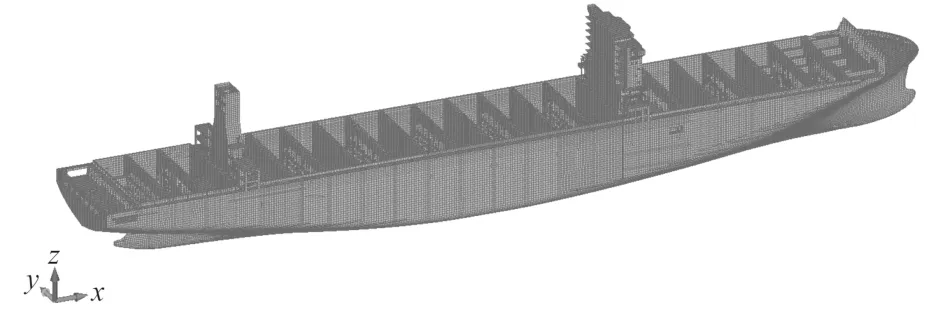
图4 测试集装箱船全船有限元模型Fig.4 Test global ship FEM of container vessel
测试计算机的CPU 为Intel Xeon E5-2 643 3.4 GHz,内存容量为64 GB,操作系统为Windows 7(64 位)。
利用Napa 软件输出总体专业的船舶舱室数据,并按照特定格式写入Excel 文件,将其作为舱室必要数据的输入文件。
导入成功后,一键运行程序即可快速、自动、准确地识别出绝大多数舱室,如首/尾尖舱、底/边压载水舱、LNG 燃料舱等封闭舱室和集装箱货舱,如图5 所示。

图5 水密舱室边界Fig.5 Watertight compartment boundary
此外,对于机舱等个别非封闭舱室,需先采用手动填补开孔的方法进行预处理,然后再进行舱室边界自动搜索。机舱搜索结果如图6 所示。

图6 机舱边界Fig.6 Engine room boundary
经多次测试,完成上述110 个舱室一键自动识别共需106 s,平均一个舱室耗时约1.0 s。经检查,结果无需修改的识别正确率约为90%,剩余的限于舱室特点和有限元模型质量,还需手动处理,耗时约半小时。总体而言,该程序识别率较高,所需时间较少,具有较强的工程应用价值。
测试结果表明,对于具有不规则、复杂形状的舱室,本文的算法能很好地实现边界搜索。
4 结语
结合实际设计和科研的需求,针对船舶有限元舱室自动识别问题进行研究,主要结论如下:
1)提出的全新船舶有限元舱室识别算法“无自由边法”,可实现舱室空间的快速智能识别,编写程序对其有效性进行了验证;
2)该算法本质是解决有限元三维封闭空间的识别问题,可拓展应用到类似的科研和开发项目中;
3)通过实例验证,该算法实用可靠,除了水密舱室,对具有大开口或小开孔的非水密舱室也适用。程序操作简单,交互界面友好,可大幅提高设计人员的工作效率。

