情境创设为数学学习赋能
王磊
在初中数学教学中,情境创设是一种非常重要的方法,教师要灵活创设多样化的问题情境,如视听情境、游戏情境、操作情境等,让学生全身心投入数学学习中,加强数学学习体验,发展数学思维,提升解决问题的能力。
创设视听情境,促进直观感知。教师将多媒体信息技术引入教学,可以丰富课堂教学形式,让学生更好地理解知识。教学“直线和圆的位置关系”时,笔者先用课件呈现“太阳在清晰的地平线上露出可爱笑脸”的视听情境,并将这种美丽的景象形象地比喻为直线和圆的关系。然后,笔者播放《日光曲》作为伴奏,在舒缓、优美的音乐伴随下,“一轮红日,从地平线上冉冉升起……”的散文诗朗诵轻轻播放出来。在视听情境下,笔者顺势引导学生思考:直线和圆有几个公共点?它们的位置关系可分为几种类型?分类的依据是什么?学生认真观察画面,很快回答出:直线和圆有0个、1个或2个公共点,直线和圆的位置关系依据公共点个数可分三种类型,分别是相离、相切、相交。最后,笔者借助几何画板,让学生通过观察,分别比较直线与圆相离、相切、相交时圆心到直线的距离,以及它们圆半径之间的数量关系。学生借助几何画板呈现的直观图,很快发现:相离时,这个距离大于半径;相切时,这个距离等于半径;相交时,这个距离小于半径。通过视听情境,学生学会运用联想、数形结合的思想方法探究问题的本质,并且探究兴趣高涨。
创设游戏情境,强化学习体验。数学游戏中蕴含着数学知识、数学思维,可以增强数学学习的趣味性,让学生在主动参与的过程中潜移默化地掌握数学知识、技能和思想方法,获得基本数学活动经验。
教学《中心对称》时,笔者先带领学生复习中心对称的概念和性质以及中心对称图形的概念,进一步强化学生的尺规作图能力。学生在回顾中明确:中心对称指把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,就说明这两个图形关于这个点对称或中心对称,这个点叫做对称中心;中心对称图形指把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
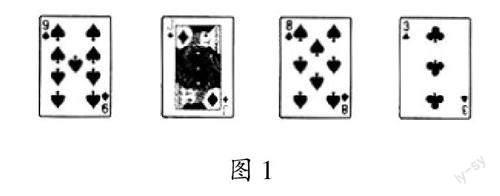
然后,笔者设计了师生互动的小游戏,让学生在参与过程中巩固、深化相关知识。如图1所示,笔者把4张扑克牌放在一张桌子上,并表示:“我闭上眼睛,你可将其中任意1张扑克牌旋转180°后放回原位,我马上就能猜出你旋转了哪一张。”学生兴趣高涨,跃跃欲试。
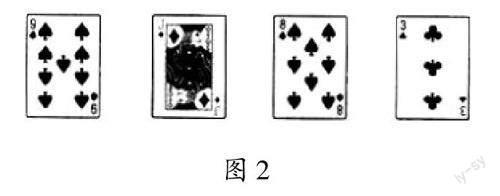
笔者闭上眼,请一名学生将其中1張扑克牌旋转后放回原位。4张扑克牌的正面如图2所示。
笔者稍加观察,便自信地说:“你旋转了方块J。”学生纷纷表示太神奇了。结合中心对称的概念和性质,以及中心对称图形的概念,学生明确了:这4张扑克牌中黑桃9、黑桃8和草花3都不是中心对称图形,只有方块J是中心对称图形;方块J旋转180°后能与原来的图形重合,其他3张都不行。这样的游戏互动激发了学生的求知欲,有助于学生养成勤于动手、乐于探究的学习习惯。
责任编辑 张敏

