基于PolyMax法的动车组齿轮箱箱体模态试验方法
赵 璐,刘焕伟,袁 韬,束玉宁,颜晓飞
(1.中车戚墅堰机车车辆工艺研究所有限公司,江苏 常州213011;2.中车常州车辆有限公司,江苏 常州 213011)
齿轮箱是高速列车的关键核心部件,用于将牵引电机产生的扭矩传递给轮对,驱动动车组的运行。深入研究齿轮箱的动态特性对列车安全、稳定运行具有重要科学参考价值[1-2]。动车组齿轮箱运行过程中承受着较大的载荷,齿轮啮合产生的振动可能激励起齿轮箱箱体的固有频率发生共振,严重时造成箱体破损漏油[3]。为避免箱体共振,应确保齿轮箱结构模态参数不能等于或接近齿轮箱持续运行时的转频、齿轮啮合频率等。
本文给出了齿轮箱模态试验研究方法,并基于PolyMax模态参数识别法[4-6],利用某齿轮箱进行模态试验,分析其固有频率、振型、模态阻尼等参数,对各阶固有频率对比结果证明,有限元计算模态与试验模态的一致性较好。这为进一步优化动车组齿轮箱设计,保障列车运行平稳性、可靠性及使用寿命具有重要意义。
1 建立齿轮箱试验模态测试系统
根据动车组齿轮箱箱体的结构特点及特性,参考国内外常用测试方法[7],同时为了保证频响函数的一致性并准确高效地完成测试,选用移动力锤法进行模态测试[8-9]。测试用软硬件包括LMS SCM05 24通道数据采集分析仪1套、PCB 356A14三轴向加速度计3个、PCB086C03力锤1把、LMS Test.Lab 16A模态测试分析软件1套。首先在齿轮箱上选择合适的测量位置并进行标注,共计70个测点,如图1所示。为了避开节点,选择了小轴承座、大轴承座、吊挂支撑部位3个测点的3个方向作为参考点。根据齿轮箱箱体的实际结构及尺寸,在LMS模态分析系统中建立简化后箱体几何模型,如图2所示。再将齿轮箱用弹簧悬吊起来,使其处于近似无边界约束条件的自由状态进行测试[8-10]。

图1 齿轮箱测试现场安装状态

图2 齿轮箱简化几何模型
2 检查测试系统可靠性
为确保在齿轮箱的线性范围内进行模态测试,任选齿轮箱上1个测点,分别采用大小不同量级的激励力对齿轮箱进行激励[11],在齿轮箱的另外1个测点进行响应测量,得到2种不同量级下的频响函数,图3为所得到的输入功率谱信号和频响函数。
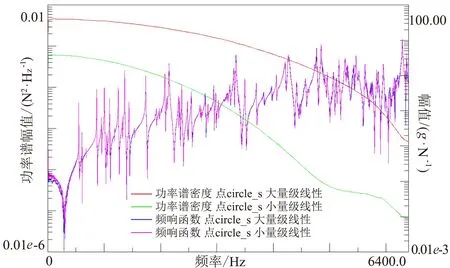
图3 力锤在不同敲击力下的频响函数一致性
可看出在这2种量级激励力下频响函数的一致性较好,整个测试过程中保持激励力大小在这2种量级之间,可确保模态测试在齿轮箱的线性范围内进行。
本次测试各参考点的相干函数如图4所示,可以看出信号相干函数整体较高,说明结构有较好线性程度同时设备有较高的信噪比,满足模态测试的条件。当输入信号与输出信号相干函数等于1时,表示该输入信号与该输出信号完全相关,该输出完全由该输入产生;相干函数等于0时,表示该输入信号与该输出信号完全不相关。依据工程经验,相干函数大于0.8代表相关情况较好。

图4 参考点相干函数
3 PolyMax法识别模态参数
PolyMax模态识别方法[5]是LMS公司推出一种多自由度时域识别法,又名多参考点最小二乘复频域法(Polyreference least squares complex frequency domain method),是最小二乘复频域法(LSCF)的多输入形式,是一种对极点和模态参与因子进行整体估计的多自由度法。
首先通过实验建立稳态图,以判定真实的模态频率、阻尼和参与因子。建立可以线性化的直交矩阵分式模型,然后基于正则方程缩减最小二乘问题,得到压缩正则方程,于是模态参数可以通过求解最小二乘问题得到。
该方法集合了多参考点法和LSCF方法的优点,可以得出非常清晰的稳态图,并且密集空间可以被分离出来,尤其在模态较密集的系统或者FRF数据受到严重噪声污染的情况下仍可以建立清晰的稳态图,识别出高度密集的模态,对每一个模态的频率、阻尼和振型都有很好的识别精度,是国际最新发展并流行的基于传递函数的模态分析方法。
试验得到的稳态图如图5所示,可以看出稳态图中各曲线能够清晰识别,且较好地反映出不同激励下的模态差异。
4 模态试验结果
测试共得到1 260组频响函数,0~2 000 Hz以内频响函数幅频图如图6所示,通过PolyMAX模块对400~1 350 Hz频段进行模态分析,选取齿轮箱箱体前10阶模态,如表1所示。
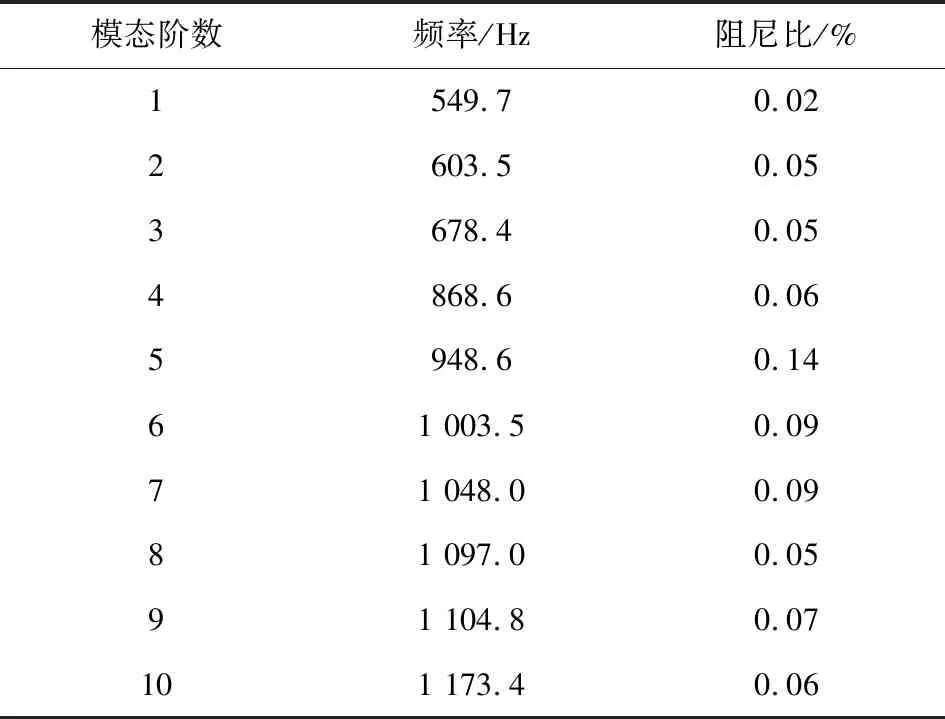
表1 齿轮箱试验模态频率和阻尼

图6 频响函数幅频图
齿轮箱箱体前4阶振型如图7所示,1阶振型表现为齿轮箱安全托弯曲振动;2阶振型为齿轮箱扭转振动;3阶振型表现为大轴承座沿Y轴摆动,4阶振型表现为齿轮箱整体的复合振动。

图7 试验模态1~4阶振型
该型齿轮箱在持续工况时的小齿轮轴转速为3 452 r/min,转频为57.53 Hz,车轴的转频为10.68 Hz,都远小于箱体的一阶模态频率(549.1 Hz),而该工况下的齿轮对啮合频率为1 035.6 Hz,高于箱体的前5阶模态频率,由于低阶模态对箱体的振动特性起主要作用[12]。
综合上述模态结果可知:在持续工况时,齿轮箱箱体不会发生共振现象。
5 结果验证
对模态试验结果进行验证的常用方法是模态判定准则(MAC 值)[6],MAC值表示模态结果的可信程度,根据模态判定准则:同阶模态振型MAC接近于1,不同阶振型MAC接近于0。由于模态测试选择的测点有限,测点的空间分辨率不足,不能唯一精确地区分各阶模态振型造成多阶模态存在相似性,造成个别不同阶模态振型MAC没有接近0。图8所示为计算得到的MAC矩阵,从矩阵图可看出试验总体结果可以接受。
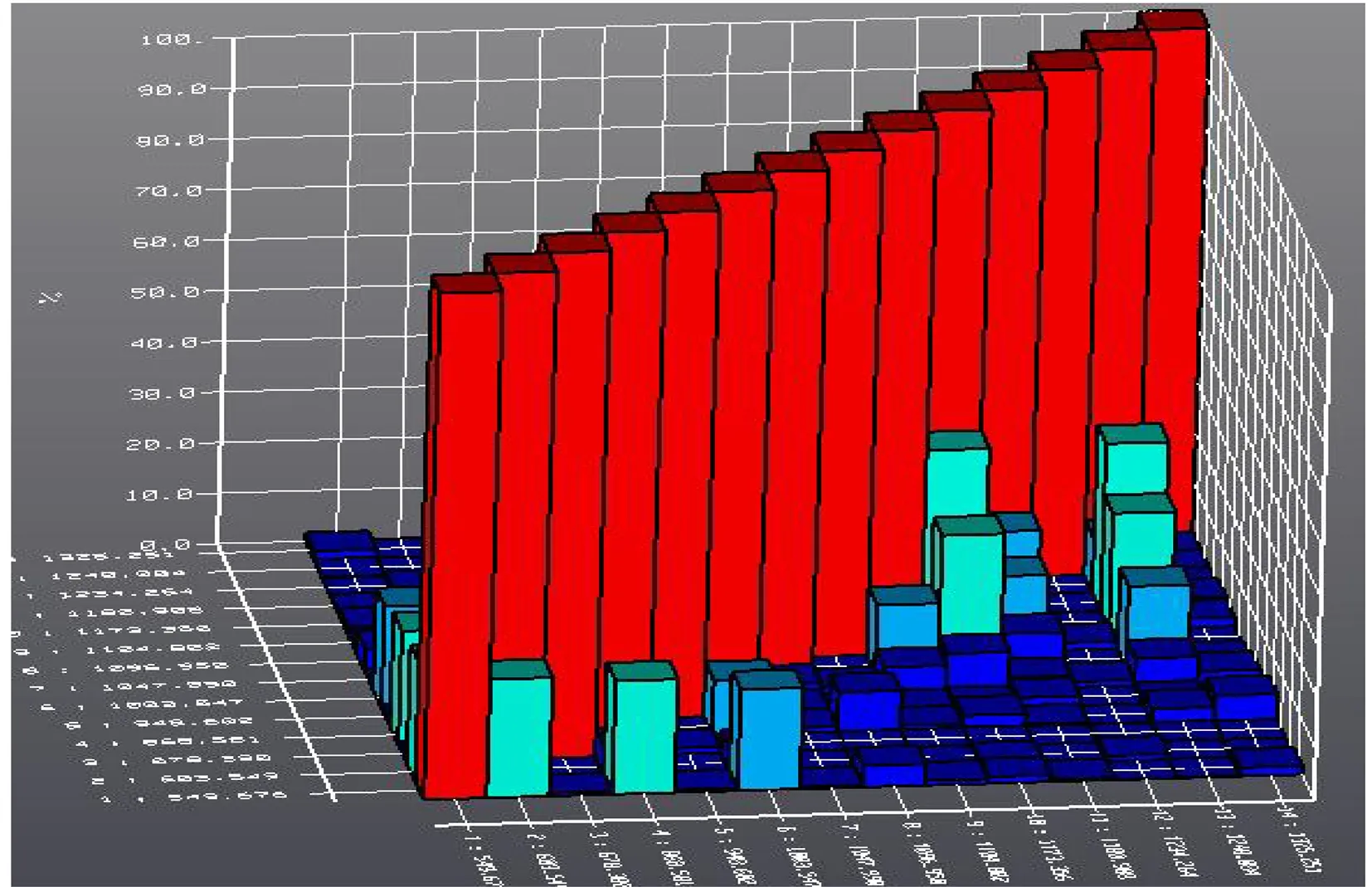
图8 模态振型MAC值矩阵图
6 齿轮箱有限元模态及模态试验结果对比
齿轮箱箱体材料牌号为AlSi7Mg0.3,密度为2 650 kg/m3,弹性模量为74 GPa,泊松比为0.33。在保证准确反映结构特性的前提下对箱体模型进行了必要的简化,略去了小孔、小倒角等特征。在计算时箱体、轴承座等模型采用四面体单元进行网格划分,如图9所示。

图9 齿轮箱箱体有限元模型
有限元计算模态与试验模态频率对比如表2所示。
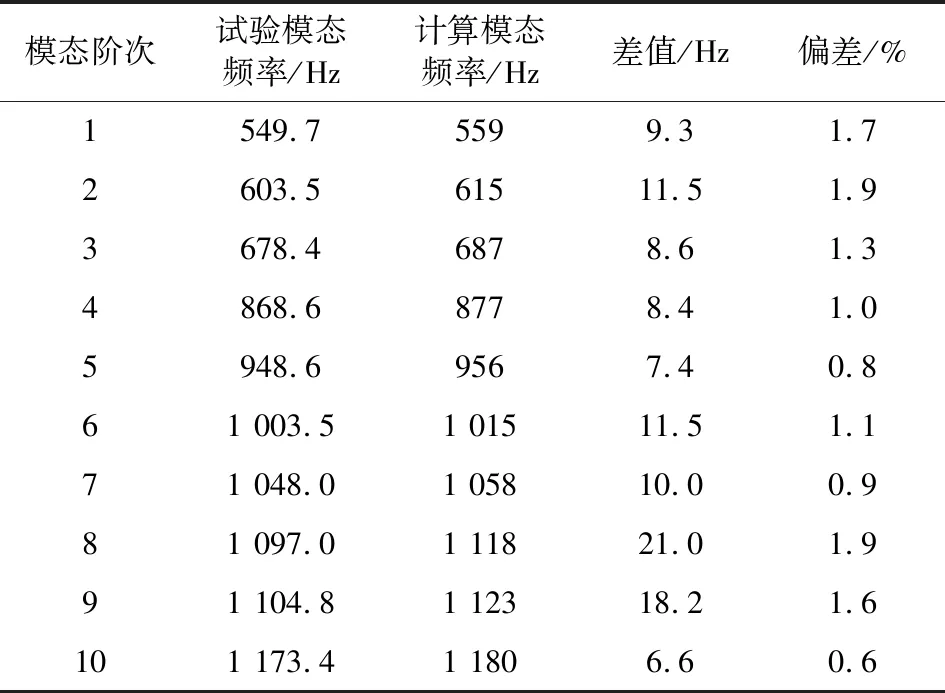
表2 模态频率对比分析表
将有限元计算模态和试验模态的频率进行对比,可以看出各阶固有频率的计算值和试验值较为接近,误差均在2%以下。说明有限元计算模态与试验模态有较好的一致性,也证明了模态试验结果可信,有限元计算结果准确可靠,模态试验结果可用于有限元模型的验证和更新。
7 结论
(1)模态试验分析结果表明,该型动车组齿轮箱箱体固有频率较为密集,且均远离持续工况时的特征频率,该型齿轮箱箱体结构设计合理。
(2)基于PolyMax法的齿轮箱箱体模态试验结果与模拟计算结果具有较好的一致性,测试可信度高,可为齿轮箱结构动力学设计提供依据,同时用于有限元模型的验证和更新。
(3)PolyMax法生成的稳态图可对高度密集的模态进行有效识别,且对每一个模态的频率、阻尼和振型都有较高的识别精度,可以排除人为主观误差因素的影响,确保模态试验分析的可靠性、准确性、高效性。

