基于MIGA算法的完全对称翼型优化设计方法研究*

张 森 高一鸣 田思宇 李华星 席德科

（1.河南理工大学机械与动力工程学院；2.华北电力大学机械工程系；3.西北工业大学航空学院）

0 引言

可逆式叶轮机械是一种具有正反向工作能力的特种流体机械设备，广泛应用于对工质流动方向快速切换有特殊需求的场合，如舰船、公路隧道的突发火灾，潮汐涡轮、水泵水轮机的双向运行，旋翼/机翼的逆流工况抑制等[1-4]。

叶轮直接反转是可逆式叶轮机械实现双向运行的主要途径，可逆翼型作为叶轮基本设计单元，其性能的优劣对可逆式叶轮机械性能起着决定性作用[5-7]。因此，开发高性能可逆翼型对可逆式叶轮机械的发展具有重要的现实意义。

相比于常规航空翼型，可逆翼型没有成熟的翼型系列，且应用场景比较特殊，因此往往需要进行原始设计。李景银等[8-9]以常规翼型为基础，按一定比例截取其头部并反向搭接，经过光滑处理后得到双头反向对称翼型，实验结果表明，翼型头部型线对升力性能影响较大，但对阻力性能影响较小。崔莹莹[10]和王晓航[11]也采用了上述方法，前者通过截取NACA66翼型的前半部分并反向搭接，得到了S 型可逆翼型，并应用于双向轴流泵设计；后者以NACA00 系列翼型族为初始翼型，以最大厚度位置为分界线，取前缘部分进行镜像拼接，最终得到完全对称翼型。Liu 等[12]研制了一种用于双向水平轴潮汐涡轮的双向对称翼型，其前后缘设计为细长型，以节省叶片材料，40%～60%弦长处的厚度较大，用于增加强度。

以上文献所述的可逆翼型设计方法，本质上均是按一定比例截取现有常规翼型的头部，然后进行反向拼接，此类方法的设计手段均是几何作图，设计结果的好坏具有较大的不确定性。此外，还有研究采用单独设计中弧线的方法来获得可逆翼型。

李超俊等[13]给出了一种双圆弧S型可逆翼型中弧线的设计方法，中弧线由两段相切的圆弧连接而成，翼型的最大厚度和最大弯度均位于圆弧中点。Spasić等[14]利用双曲线设计出S型的中弧线，并将完全对称翼型布置到该中弧线上，得到了S 型可逆翼型。Chacko 等[15]利用两条对称的抛物线构建中弧线，厚度分布选择Göttingen775翼型，叠加后得到新的S型可逆翼型。Chacko等[16]还实验研究了后缘切割对可逆翼型气动特性的影响，发现在小攻角下，随着切割长度的增加，升力系数在正向模式下增大，在反向模式下减小。黄典贵[17]对S型可逆翼型的厚度分布和中弧线分别进行设计，中弧线采用抛物线方程，厚度分布采用基于NACA4位数系列翼型反向搭接得到的厚度分布。

以上研究表明，当前可逆翼型的设计方法主要是单独设计S型中弧线并叠加厚度分布以及利用现有翼型对称或非对称拼接，这些设计方法的设计空间有限，设计结果的性能难以预测，具有较大的局限性。因此，相比于常规航空翼型，可逆翼型的设计方法尚有较大提升空间，其气动特性还需开展系统深入研究。

本文以可逆翼型中最基础的完全对称翼型为研究对象，提出了基于贝塞尔曲线的完全对称翼型型线参数化设计方法，并制定了详细的优化策略，基于Isight自动优化平台，结合ICEM网格划分和Fluent数值仿真，采用多岛遗传算法实现完全对称翼型的优化设计。

1 参数化设计方法的建立

合理的参数化方法是实现翼型优化设计的先决条件。目前，常用的参数化方法主要有形函数扰动法、外形参数化方法和解析函数法[18-19]。

鉴于本研究的对象为完全对称翼型，翼型型线为光滑曲线，选用解析函数法能够很好地拟合翼型。其中Bezier多项式具有控制参数少，拟合精度高且操作方便等特点，适用于对完全对称翼型进行函数解析。因此，选择6控制点的5阶Bezier多项式对翼型型线的四分之一进行参数化表达，如式（1）所示，进而设计出完整的完全对称翼型。

式中，P为控制点坐标；t为参变量，t∈[0,1] 。

为了保证翼型型线光滑连续，令控制点P0位于坐标原点，即翼型前缘点，控制点P1位于P0正上方，使得翼型前缘处切线为y轴，如图1所示，令翼型的弦长c=1。同理，令控制点P5横坐标为c/2，纵坐标为最大厚度的一半即T/2，且控制点P4的纵坐标与控制点P5相同，进而保障翼型型线在最大厚度处的切线平行于x轴。采用上述方法，可以通过6个未知的控制点坐标对翼型型线进行控制。

图1 完全对称翼型的参数化表达Fig.1 Parameterized expression of fully symmetric airfoil profile

此外，为了避免翼型型线出现拐点，令位于中间区域的控制点Pi的横纵坐标均大于控制点Pi-1的横纵坐标。基于上述原则，得到贝塞尔曲线的控制点坐标如式（2）和式（3）所示。

式中，X和Y分别为控制点的横坐标和纵坐标；T为翼型的最大相对厚度；和分别为横纵坐标控制系数，其中∈(0,1)，∈(0,1)，通过引入无量纲的横纵坐标控制系数，能够更方便地对控制点的空间位置进行控制。

2 优化设计方法的构建

上述完全对称翼型参数化设计方法中出现了6个未知的控制点坐标控制系数和翼型最大厚度T共7 个设计变量，具有较大的设计空间，很难人为选择出最优的翼型。因此，需要借助计算机程序求得最优翼型。

2.1 优化平台搭建

基于Isight平台搭建了完整的完全对称翼型优化设计流程，如图2所示。该优化流程主要包括4个环节，即翼型型线设计、网格划分、流场仿真和目标函数求解。

图2 优化流程Fig.2 Optimization flow chart

首先，采用Fortran语言编写完全对称翼型参数化设计程序代码，并生成可执行文件，通过更改文件的输入参数，生成新的翼型型线坐标点文件；然后，对绕翼型流场进行非结构化网格自动划分，此步骤通过ICEM软件的rpl脚本文件实现；其次，使用Fluent 对不同攻角下的绕翼型流场进行求解，并将仿真预测的结果传递给目标函数；最后，通过优化算法求解目标函数的最优解。

2.2 数值模拟方法

选用基于密度的求解器进行流场计算，湍流模型选择SST k-ω 模型。边界条件设置为压力远场，翼型表面定义为无滑移壁面，流体域中的工质定义为空气，密度为1.2kg/m3，运动粘度为1.6×10-5m2/s。为了能够获得正确的升力和阻力系数，使用式（4）中所示的流向矢量进行分解计算。

式中，α为来流攻角；L和D分别为升力和阻力；L′和D′为基于Fluent网格坐标系表示的气动力分量。

绕翼型流场设置为半径为10倍弦长的圆形区域，采用非结构化网格对流体域进行O型网格划分，首层网格的厚度为0.23×10-5m，对应的y+=3。

在2.1 节建立的优化流程中，需要对绕翼型流场进行大量仿真计算，因此需进行网格的无关性验证，以选择出能够平衡计算精度与计算时间的最小网格数。以文献[11]提供的具有详细风洞实验数据的椭圆翼型作为参考模型进行网格无关性验证，其主要设计参数如表1所示。

表1 参考翼型模型的主要设计参数Tab.1 Main design parameters of the reference airfoil profile model

在首层网格厚度保持不变的前提下，通过调整径向和周向网格节点分布规律得到4 种网格配置，如图3 所示。在4°攻角下，对上述4种网格配置的流体域进行仿真计算，结果如表2所示。

表2 不同网格配置下的计算结果Tab.2 Simulation results under different grid configurations

图3 网格配置Fig.3 Grid configurations

从表2中可以看出，随着网格节点数的增加，椭圆翼型的气动性能计算结果较为稳定，综合考虑计算时间成本和计算精度，最终选择节点数为80975 的网格配置进行翼型优化设计。

2.3 数值方法验证

为了验证数值方法的可靠性和湍流模型的适用性，分别选用SST k-ω 模型、RNG k-ε 模型和Spalart-Allmaras 模型对参考模型的气动性能进行预测，其中RNG k-ε模型选用增强壁面函数处理，结果如图4所示。

图4 气动性能曲线Fig.4 Aerodynamic performance curves

从图4(a)中所示的Cl-α曲线可以看出，当α∈[3°,12°]攻角时，三种湍流模型的预测结果与实验数据之间均表现出了较高的吻合度，当α∈[3°,12°]攻角时，SST k-ω 模型、RNG k-ε 模型和Spalart-Allmaras 模型的升力系数预测结果与实验数据的平均相对误差分别为4.21%、4.90%和4.34%。但在α≤3°和α≥12°的攻角范围内，由于实验数据表现出了较强的非线性，预测结果与实验数据之间存在较大差异。

图4(b)中还给出了Cd-α曲线，从图中可以发现，三种湍流模型预测的Cd-α曲线变化趋势表现出了较高的一致性，且当α∈[3°,14°] 攻角时，SST k-ω 模型和Spalart-Allmaras 模型预测结果与实验曲线具有较高的吻合度，SST k-ω 模型、RNG k-ε 模型和Spalart-Allmaras 模型的阻力系数预测结果与实验数据的平均相对误差分别为3.94%、36.52%和6.37%。此外，在小攻角区域，Cd-α预测曲线与实验曲线的变化趋势表现出了较大差异，造成这一现象的原因为:一方面，受加工精度所限，实验模型与仿真中的椭圆会存在一定差异，从而造成实验数据与数值仿真结果存在误差；另一方面，影响实验结果的因素众多，尤其在小攻角范围，实验结果很容易受到外界因素的干扰，而数值仿真是在较理想状态下进行的，因此会导致两者之间存在偏差。此外，Cd-α实验曲线在小攻角附近的非线性从侧面印证了上述分析。

对比结果显示，SST k-ω 模型和Spalart-Allmaras 模型均能够对参考模型的气动性能进行较好的预测，其中SST k-ω模型的预测结果与实验数据吻合度最好。因此，针对完全对称翼型的优化设计问题，本文所采用的数值方法是可靠的，所选用的SST k-ω湍流模型满足适用性要求。

2.4 优化算法

本文中设计变量较多，设计空间较大，无法人工求得最优解，需借助算法进行自动寻优。遗传算法（GA）和粒子群算法（PSO）等优化算法是解决这类问题的有效手段。本文所采用的多岛遗传算法（Multi-Island Genetic Algorithm，MIGA）作为广泛应用的改进遗传算法，不仅具有传统遗传算法强大的全局最优解搜索能力，同时克服了传统遗传算法运算速度慢和复杂问题求解困难的局限性。

MIGA 算法将初始种群划分为多个称为“岛”的子种群，并对每个子群体分别执行传统的遗传操作，如选择、交叉、变异等。然后，从每个“岛”上选择一些满足迁移条件的个体，定期迁移到不同的“岛”上，这种迁移操作可以有效地增强种群的多样性，从而防止发生“早熟”问题。最后，当遗传代数达到最大值MaxGen 时，优化结束[20-23]。MIGA算法的进化过程如图5所示。

图5 MIGA算法进化过程Fig.5 Evolution process of MIGA algorithm

MIGA 算法是一种基于群体分组的并行性遗传算法，通过迁移等操作增加了整体的交叉和变异概率，不仅可以维持种群的物种多样性，同时还能够有效抑制过早收敛的现象[24-27]。

2.5 目标函数

以提高设计攻角处的升力系数同时降低阻力系数为设计目标，目标函数定义为式（5）。

式中，n表示所选取的设计攻角数；ωi表示权重，i=1,2,…n；表示翼型在设计攻角下的升力系数，Cd|αi表示翼型在设计攻角下的阻力系数；表示翼型在设计攻角下期望得到的升力系数，表示翼型在设计攻角下期望得到的阻力系数。

3 结果与分析

为了验证本文构建的完全对称翼型优化设计方法，以相对厚度为16%的椭圆翼型为参考[11]，设计了一款翼型，即优化翼型A，具体设计参数见表1。对于优化翼型A，约束其相对厚度与参考翼型相等，即TA=0.16，其他设计变量的约束见表3。

表3 设计变量约束Tab.3 Constraints of design variables

此外，为了保障数值预测结果的可靠性，设计攻角选择位于升力系数曲线的线性段，且与实验数据吻合度较高的攻角区间，即4°，8°和12°攻角，并取权重值ω1=0.4，ω2=0.4，ω3=0.2。MIGA算法的参数设置如表4所示。

表4 MIGA算法参数Tab.4 Parameters of MIGA algorithm

经过600 次迭代计算，优化设计得到的完全对称翼型型线如图6所示。

图6 完全对称翼型型线Fig.6 Fully symmetric airfoil profiles

从图6可以看出，相比于参考翼型，优化翼型A的型线曲率在前缘点、后缘点和最大厚度处均较大，其他部分则较小。详细的优化设计结果见表5。

表5 优化结果Tab.5 Optimization results

图7中给出了Re=2.5×106时，优化翼型A和参考翼型在不同攻角下的气动性能比较，结果显示，优化翼型A 在设计攻角下的气动性能相比于参考翼型有所提升。在4°，8°和12°攻角下，优化翼型A 的升力系数分别增加了6.15%，6.95%和7.01%，阻力系数分别降低了7.09%，5.57%和3.61%，升阻比分别增加了14.22%，13.47%和11.47%。

图7 优化翼型气动特性曲线Fig.7 Aerodynamic characteristic curves of optimized airfoils

从图7(a)中还可以看出，在非设计攻角下，优化翼型A 的升力特性均优于参考翼型，且随着攻角的增大，升力特性提升越明显。此外，如图7(b)所示，在α∈[0°,13°]攻角范围内，优化翼型A 的阻力特性也表现出了显著提升，但当α≥13°攻角时，其阻力特性劣于参考翼型。

图7(c)给出了优化翼型A和参考翼型的升阻比对比曲线，α∈[0°,15°]攻角范围内，优化翼型A 的升阻比均优于参考翼型。随着攻角的增大，优化翼型A相较于参考翼型升阻比提升越来越大，但当α≥9°攻角时，优化翼型A 升阻比提升幅度逐渐减小。

为了进一步分析优化翼型A 和椭圆翼型性能差异的内在原因，在图8 中分别给出了Re=2.5×106时，4°，8°和12°攻角下的压力系数Cp分布以及翼型上下表面Cp,d-Cp,u的对比结果。

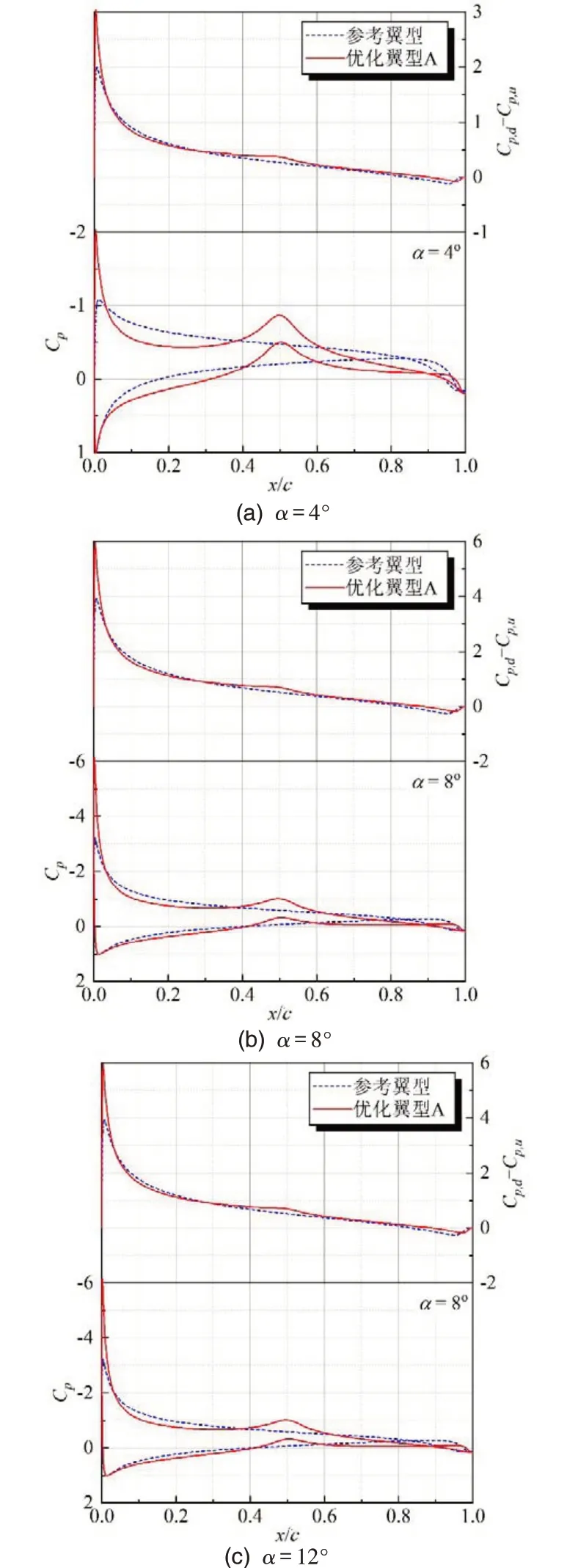
图8 4°，8°和12°攻角下的翼型表面压力系数分布Fig.8 Pressure coefficient distribution of airfoil surface at angles of attack of 4,8 and 12 degrees

从图8中可以看出，在不同攻角下，参考翼型与优化翼型A的Cp分布对比结果表现出较强的规律性：

1）在前缘点附近，两者的下表面Cp分布是一致的，而优化翼型A的上表面Cp峰值则远小于参考翼型，这是由于前者在前缘点处的型线曲率增大所造成的；

2）在xc∈(0.04,0.4)⋃(0.6,0.95) 的区域，优化翼型A上下表面的Cp值相比于参考翼型均较大，造成这一现象的原因在于，优化翼型A 在该区域的型线比较平坦，其曲率小于参考翼型型线；

3）在最大厚度附近xc∈(0.4,0.6)的区域，优化翼型A上下表面的Cp分布均呈现出驼峰状，且小于参考翼型相应的Cp分布，该现象是由于最大厚度附近的型线曲率较大所造成的；

4）在后缘点附近，优化翼型A上下表面的Cp值小于参考翼型相应的Cp值，且上下表面Cp的差值Cp,d-Cp,u也较小。

此外，为了更加直观的分析翼型表面载荷分布规律，图8中还给出了翼型上下表面Cp,d-Cp,u的分布曲线。结果显示，在不同攻角下，优化翼型A 的Cp,d-Cp,u值虽然在xc∈(0.04,0.3)⋃(0.96,1)的区域小于参考翼型，但其他区域的载荷均有提升，尤其是前缘点、最大厚度和接近后缘点附近的区域，这正是优化翼型A升力性能得到提升的直接原因。

同时，相比于参考翼型，优化翼型A 的翼型载荷在xc∈(0.04,0.3)的区域减小，而在xc∈(0.3,0.96)的区域增加，使沿弦线方向翼型载荷分布更加均衡，这也是优化翼型A在4°和8°攻角下阻力系数减小的主要原因。然而，当攻角为12°时，虽然优化翼型A 和参考翼型的总体载荷分布趋于相同，但优化翼型A 在前缘点附近的载荷明显较大，从而导致其阻力性能下降。

上述研究结果表明，采用本文构建的优化设计方法设计得到的优化翼型A 的气动性能相较于参考翼型有了显著的提升，印证了该设计方法的可靠性和实用性。

4 结论

1）提出了一种基于Bezier 曲线的完全对称翼型参数化设计方法，通过6控制点5阶Bezier多项式对完全对称翼型的型线进行参数化表达，并通过6个无量纲的横纵坐标控制系数和最大相对厚度控制翼型型线。该方法能够方便地对完全对称翼型型线进行参数化表达，且拥有足够大的设计空间。

2）基于Isight平台搭建了完整的完全对称翼型优化设计流程，通过采用Fortran 语言编写参数化设计程序代码，并与ICEM 网格划分和Fluent 数值仿真集成到Isight 自动优化平台的方法，借助MIGA 算法实现了完全对称翼型的自动优化设计。不仅实现了优化过程的完全自动化，而且能够快速找到最优解。

3）以相对厚度为16%的椭圆翼型为参考，设计了一款翼型，即优化翼型A。结果显示，相比于参考翼型，优化翼型A的厚度分布减小，在前缘点和最大厚度附近型线曲率较大，导致上表面压力系数分布减小，并在最大厚度处呈现出驼峰状。优化翼型A的升阻比较参考翼型有着明显提升，且高效升阻比范围内提升更为显著，同时优化翼型A沿弦线方向翼型载荷分布更加均衡，使其气动性能相比于参考翼型有了显著提升，印证了本文构建的优化设计方法的可靠性。