路基空洞对混凝土道路板时频振动特性影响模拟研究

史 吏,徐健洲

(浙江工业大学 土木工程学院,浙江 杭州 310023)

近年来,城市道路塌陷灾害频发,造成了巨大的人员伤亡和财产损失。2020年1月13日青海省西宁市发生路面坍塌,一辆公交车被陷[1];2020年6月30日浙江省杭州市同日出现2处路面塌陷,多辆汽车被陷[2]。路基空洞是导致道路塌陷的直接原因,地下施工扰动、地下管线渗漏等因素是路基空洞的主要诱因,若不及时发现处置,路基空洞持续扩大极易导致路面塌陷。由于路基空洞的强隐蔽性,路面塌陷灾害预测难度大,路基空洞探测问题亟待解决。车载地质雷达是目前最常用的路基空洞探测方法[3],相较于其他探测方式,该方法虽然检测快速且基本不会影响道路交通,但是其单次扫描的作业方式导致所需要的人力、设备成本相对较高,难以应用于大范围城市道路的长期连续监测。路基空洞的存在和发展会改变路基的刚度和质量分布,进而影响道路结构的振动特性,若能建立基于道路结构响应的路基空洞探测方法,可大幅降低成本,有助于智慧城市建设。针对路基空洞影响下的路基振动特性问题,Xiao等[4]认为路基空洞会给路基结构内部引入新的边界条件;Lee等[5-7]发现路基空洞导致弹性波入射至空洞边界时产生明显的散射现象;Gelis等[8]利用有限差分法研究了二维路基中圆形空洞对地表的振速及Rayleigh相速度的影响;Stefania等[9]采用有限单元法研究了地震荷载下含有矩形空洞的路基的场地放大效应,结果表明其地表振动会在5～12 Hz明显变大。以上研究综合表明路基空洞会明显影响路基的振动特性,并提供了一些可用于路基空洞监测的力学指标。然而,上述分析中的荷载条件与路基实际承受的车辆荷载相差较大,有必要针对车辆交通荷载开展研究[10]。

现有考虑车辆荷载的道路结构动力响应研究大多从道路板的支承条件出发,建立混凝土道路板振动分析模型[11],从而呈现动模量[12]、沥青应变[13]、应力[14]和变形[15]等内容,基本未见考虑带空洞路基的振动特性研究报道。笔者首先利用有限元软件ABAQUS,建立含空洞的路基有限元模型;然后结合自定义的车路耦合(VRI)单元[16],开展瞬态响应分析,并结合模态和稳态分析了瞬态响应特征;最后研究对比了空洞几何特征以及道路/路基模量比对道路板时频振动特征的影响。研究结果可为基于道路结构振动响应的路基空洞监测提供重要参考。

1 有限元模型

1.1 模型尺寸

将道路结构简化为单层道路板,同时将路基考虑为三维均质体,建立如图1所示的带空洞路基—混凝土道路板三维耦合振动分析模型。模型的几何尺寸、边界条件和荷载条件等均参照工程实际设定,道路板尺寸主要参考了二级公路标准[17],路基尺寸则主要考虑在尽可能降低边界反射的同时降低运算量,具体尺寸如表1所示。

表1 道路模型几何尺寸

将路基空洞在纵剖面内(x-z平面)简化为椭圆,在横剖面(y-z平面)方向假设该椭圆贯穿路基。蒋恺[18]对国内125起道路塌陷灾害的统计分析表明大部分路基空洞深度都在4 m以内。因此,以短轴1 m、长轴2 m、中心埋深2 m的椭圆柱体空洞作为分析对象。同时,为了对比空洞大小对振动特征的影响,补充考虑短轴2 m、长轴4 m、中心埋深2.5 m的“大洞”,具体示意图如图1,2所示。

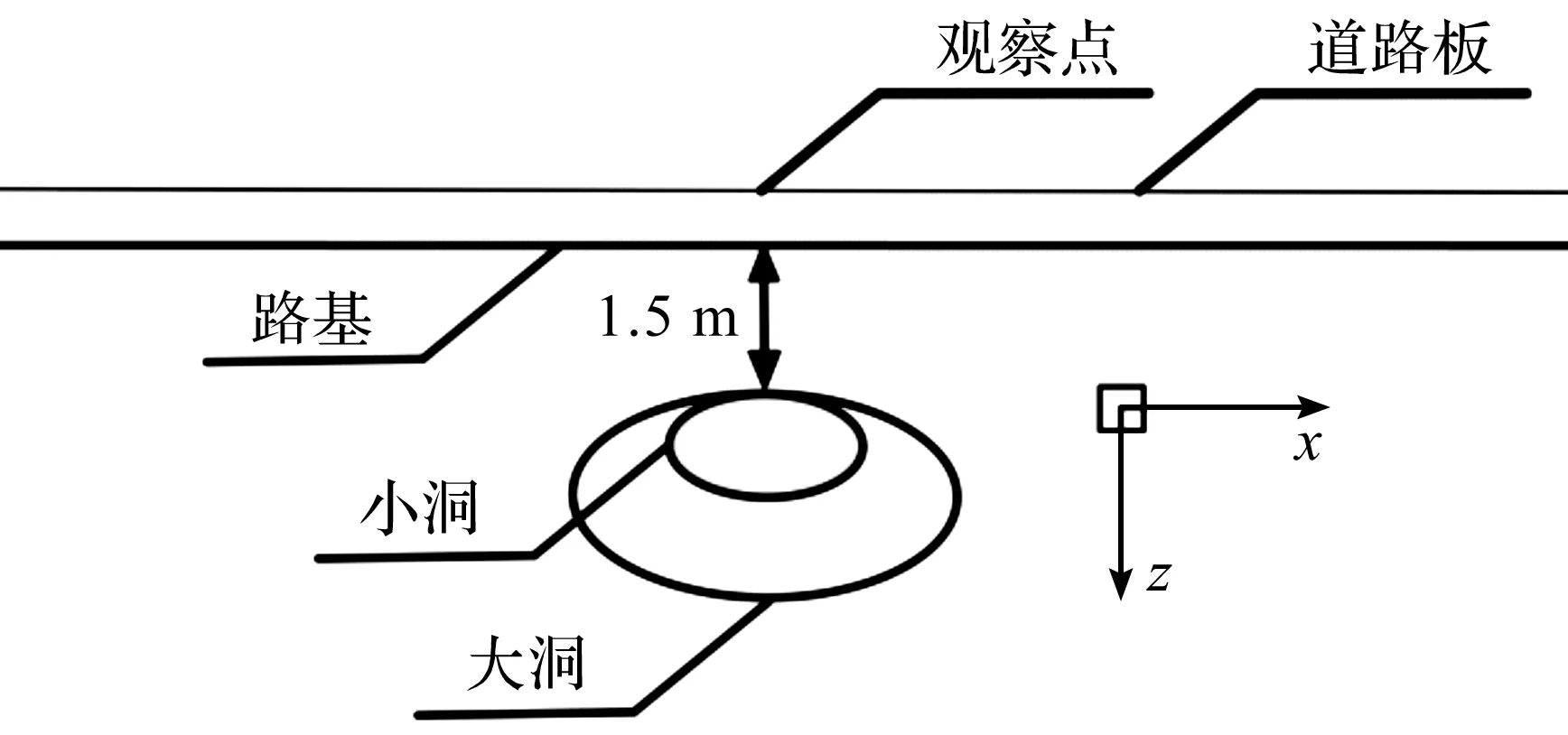
图1 路基空洞位置示意图Fig.1 Side view on location of underground cavity

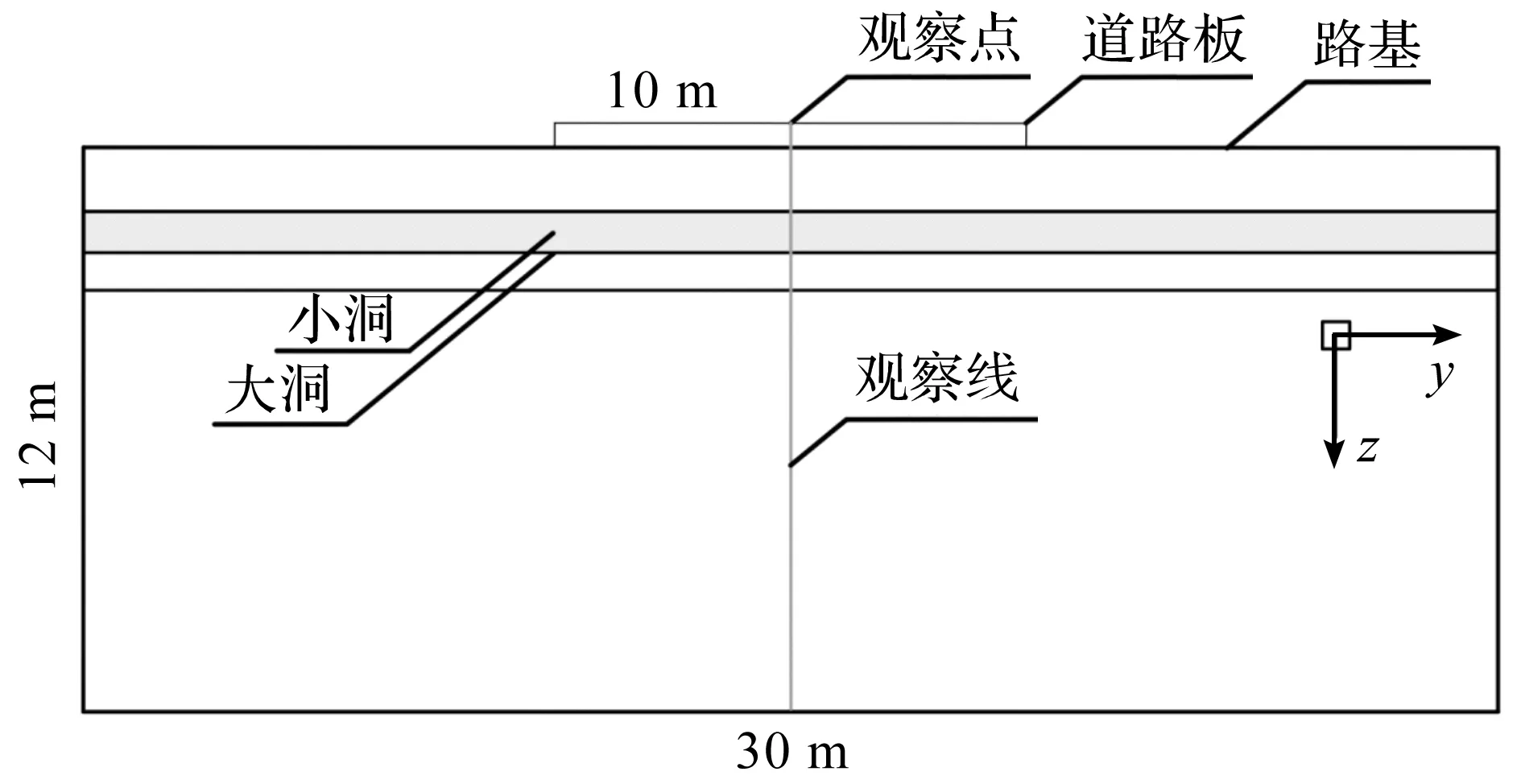
图2 路基空洞位置示意图(横剖图)Fig.2 Cross-section view on location of underground cavity

1.2 材料参数

道路板材料考虑为C30混凝土,路基材料考虑为均质黏土,材料参数如表2所示,其中道路板/路基模量比值为Ec/E=600。

表2 道路材质参数

1.3 网格划分与边界条件

在有限元模拟中,网格划分与边界条件会对计算结果产生很大影响[19]。对于车辆荷载引起的路基道路和路基振动而言,50 Hz以内的低频振动包含了大部分能量[20]。考虑最高振动频率fmax=50 Hz,估算路基的最短振动波长λmin,计算式为

(1)

(2)

(3)

式中G为路基土剪切模量。Kuhlemeyer等[21]提出,当最短波长含有5～8个单元时可满足动力计算的精度要求,因此道路板最大单元尺寸取为0.25 m。同时,为了提高运算效率,道路板正下方路基单元的尺寸取为0.25 m,并向板外围及深度方向线性增大单元尺寸,模型边缘处路基的最大单元尺寸为1 m,网格划分如图3所示。

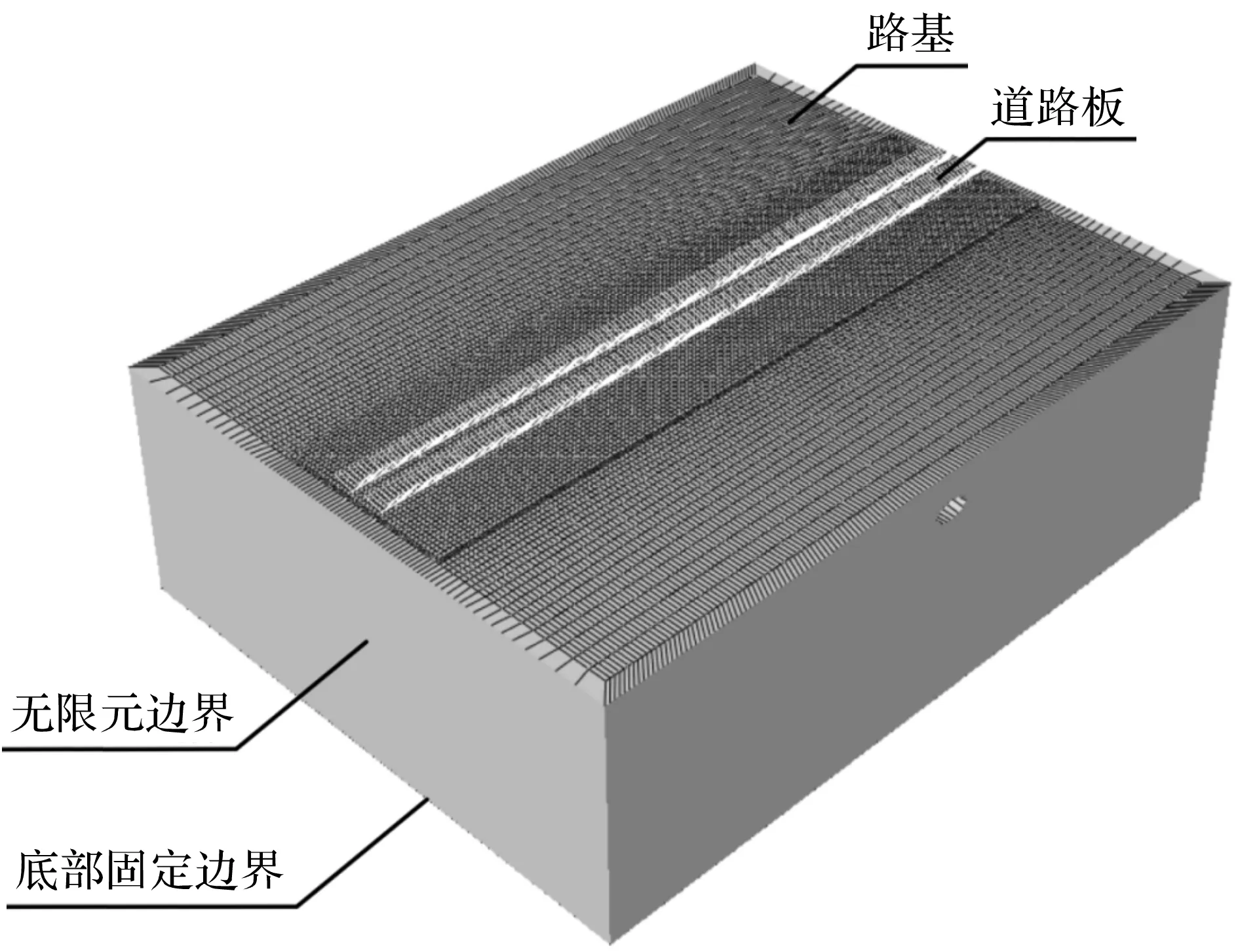
图3 网格划分示意图Fig.3 Finite element mesh of road model

移动车辆荷载在路基中产生的应力波传导至模型截断边界时会产生反射波,从而影响模拟结果的正确性。为尽量减少边界反射波,模型四周使用无限元边界(CIN3D8),模型底面为完全固定约束以考虑下卧硬土层。路基与道路板之间采用绑定(Tie)接触,采用六面体缩减积分单元(C3D8R)离散道路板和路基。

1.4 车辆荷载

已有研究表明在达到临界速度前,路基振动幅值随着荷载移动速度增加而增大[22]。考虑到城市道路多限速60 km/h,此处取15 m/s匀速前进的典型六轮卡车作为激振荷载。利用笔者开发的车路耦合(VRI)单元子程序[16]施加移动车辆荷载至道路板,以模拟车辆开行,如图4,5所示。

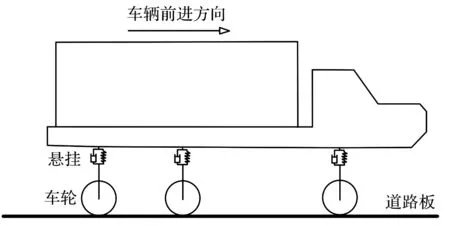
图4 ABAQUS VRI UEL模型示意图Fig.4 VRI UEL model in ABAQUS

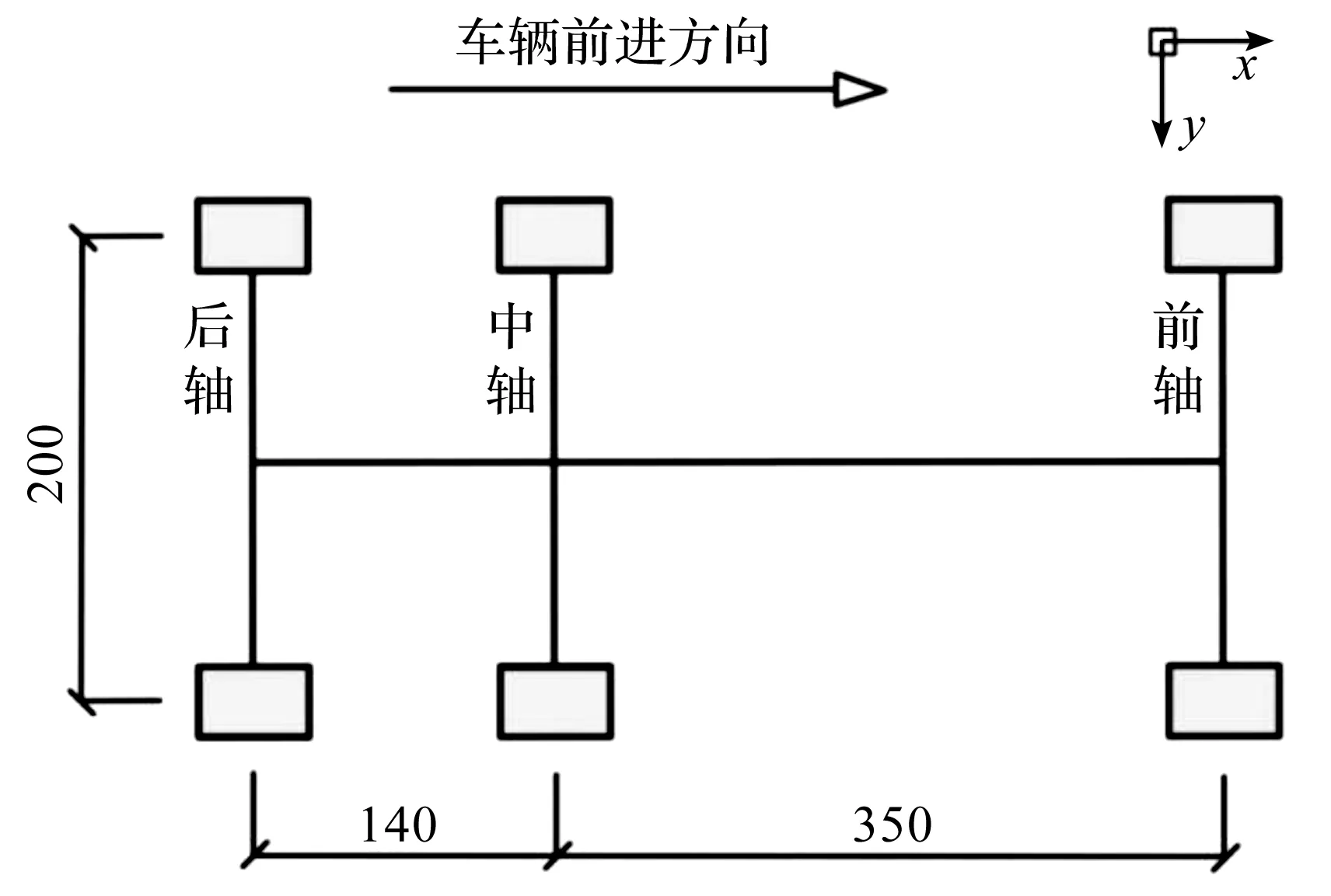
图5 车轮分布位置示意图(单位:cm)Fig.5 Diagram of wheel spacing (unit: cm)

VRI单元不需要迭代即可完成车辆和道路的动力耦合,车辆模型参数如表3所示,其中悬挂参数参考文献[23]取值。实际工程中,道面会存在高低不平顺,从而加剧轮路的耦合振动。VRI虽然可以方便地考虑道路不平顺,但会引入各波长不平顺的参数激振频率,可能干扰后续模型特征响应频率的解译,因此暂不考虑道路不平顺。

表3 车辆模型参数

2 振动特性时域分析

2.1 道路板振动时程曲线

选取车辆行进路径中线的路板中点为观察点,如图2所示。观察点的竖向振动位移和速度时程曲线如图6,7所示。由图6可知:当车辆荷载经过观察点正上方时,位移响应达到最大值。路基有空洞时,由于土体缺失,路基刚度减小,竖向位移峰值明显大于无空洞情形。然而,观察图7可知路基空洞对竖向振速的影响并不明显。

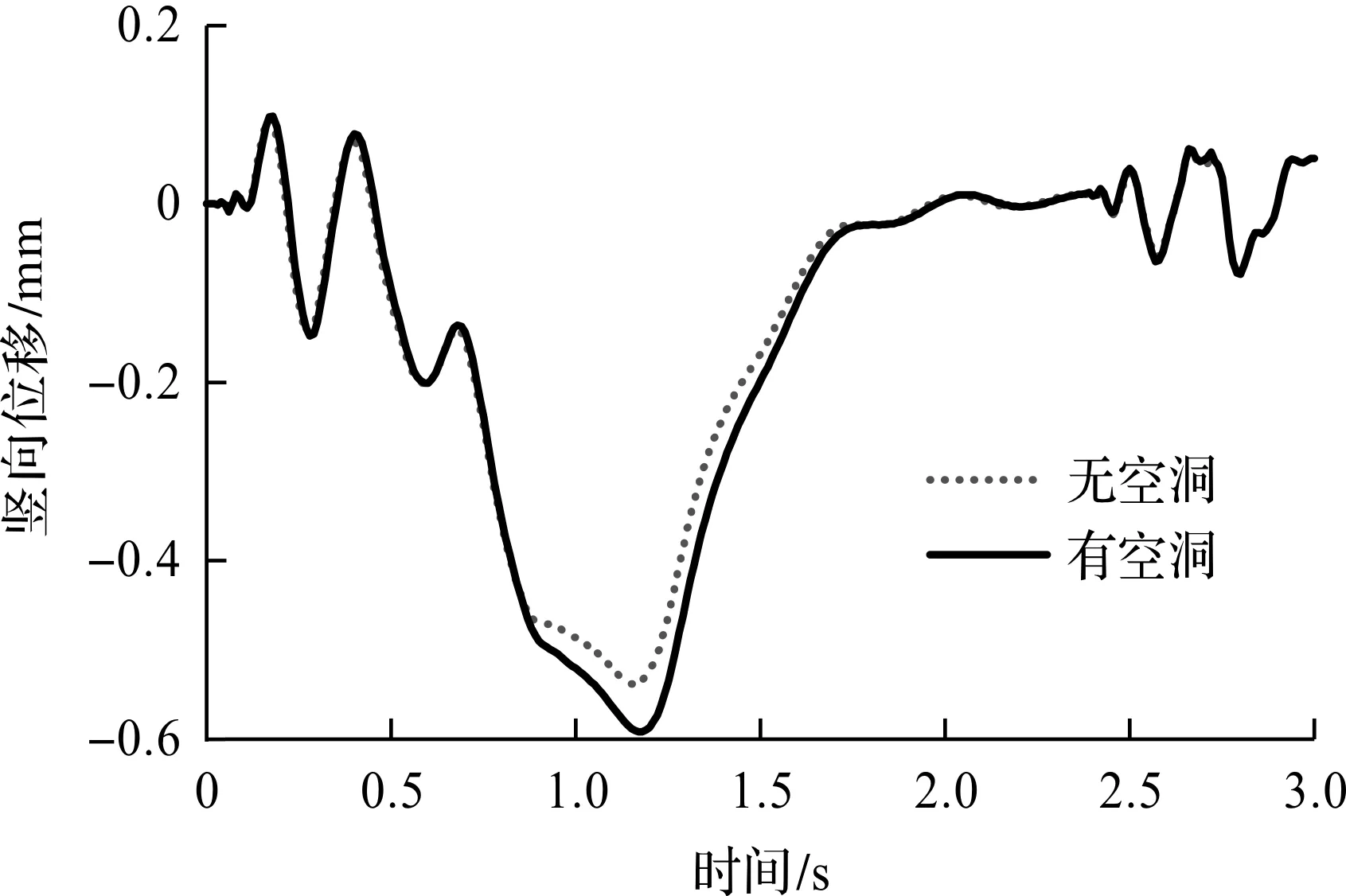
图6 路基空洞对道路板振动位移的影响Fig.6 Influence of underground cavityon vibrational displacement

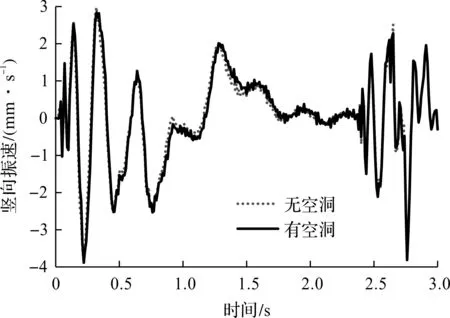
图7 路基空洞对道路板振动速度的影响Fig.7 Influence of underground cavityon vibrational velocity

2.2 路基振动位移分布

沿上述观察点设置竖向观察线,如图2所示。当车辆处于观察线正上方时,提取竖向振动位移,如图8所示,可见地表位置处的路基位移最大,且路基位移随着路基深度增大而迅速减小。空洞对其上部土体位移分布影响很大(位移放大约0.3倍),对其下部土体影响随着深度增加而迅速变小,深度大于5倍洞径后空洞的影响变得不明显。

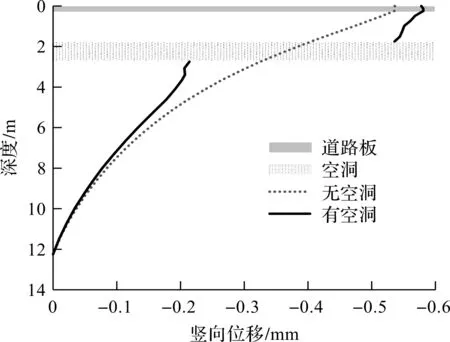
图8 竖向位移沿深度分布图Fig.8 Distribution of vertical displacementalong ground depth

3 振动特性频域分析

路基存在空洞与否,对混凝土板的瞬态振动位移影响明显大于振动速度。然而,路面振动速度的获取远比振动位移便捷,为了获取更为明显、在路基空洞探测中更有价值的判定指标,进一步在频域内展开研究。

3.1 频谱分析

将2.2节中道路板中点的竖向位移和速度时程进行傅里叶快速变换(FFT),以获得振动响应的频谱,如图9,10所示。其中,位移频谱主要集中在10 Hz以内,因而横轴上限设为15 Hz。由图9可知:在3.01,4.01,5.69,9.03 Hz等频率附近,带空洞路基的位移响应峰值虽然略高于无空洞情形,但是差异并不明显。应指出,上述峰值频率中包括了道路板—路基系统的部分特征频率。由图10可知:考虑空洞时的速度频谱与无空洞时明显不同,有空洞时4.9,8.5,12.5 Hz等频率所对应的振速峰值更大。

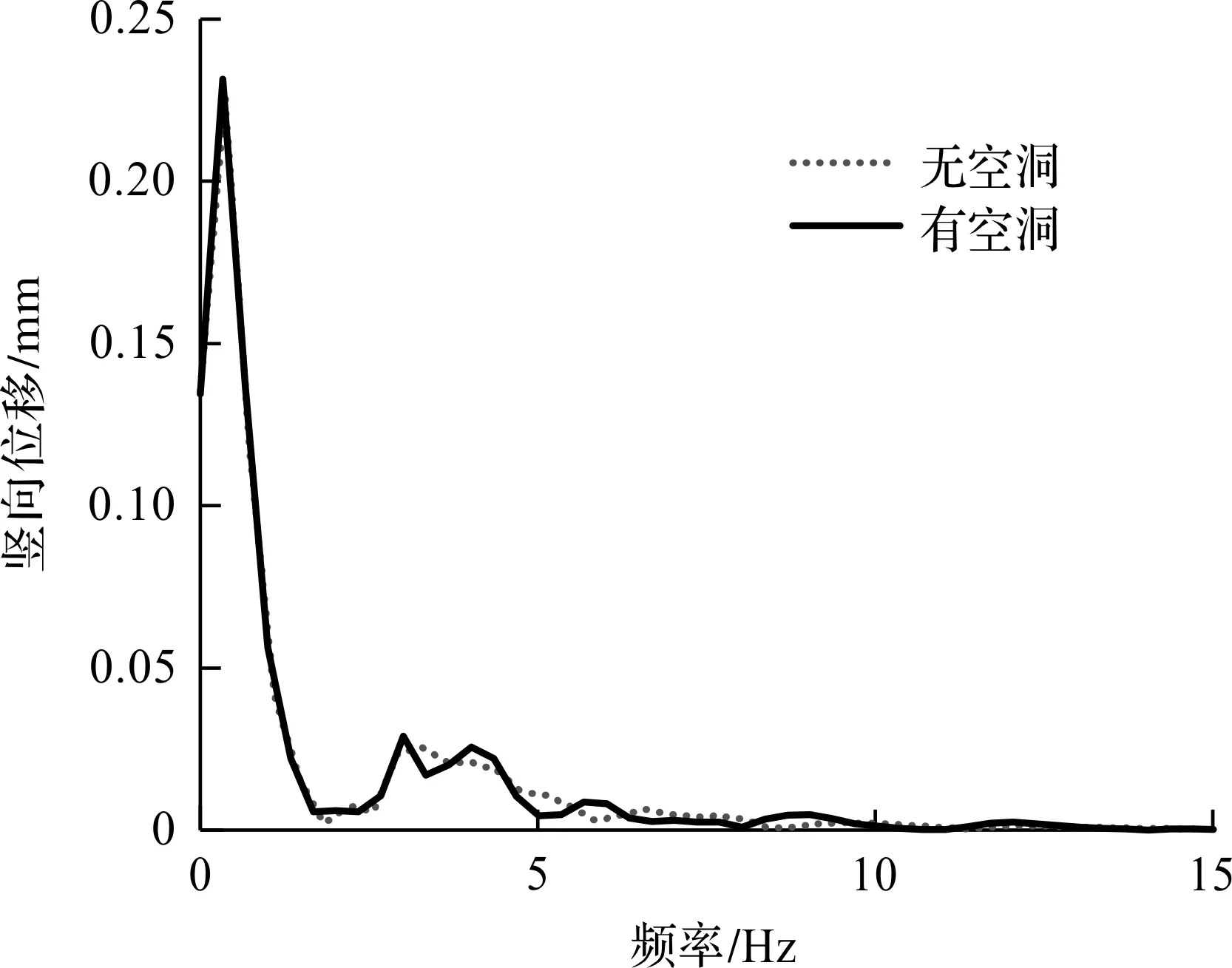
图9 道路板竖向位移的频谱曲线Fig.9 Spectrum of vertical displacement of road slab

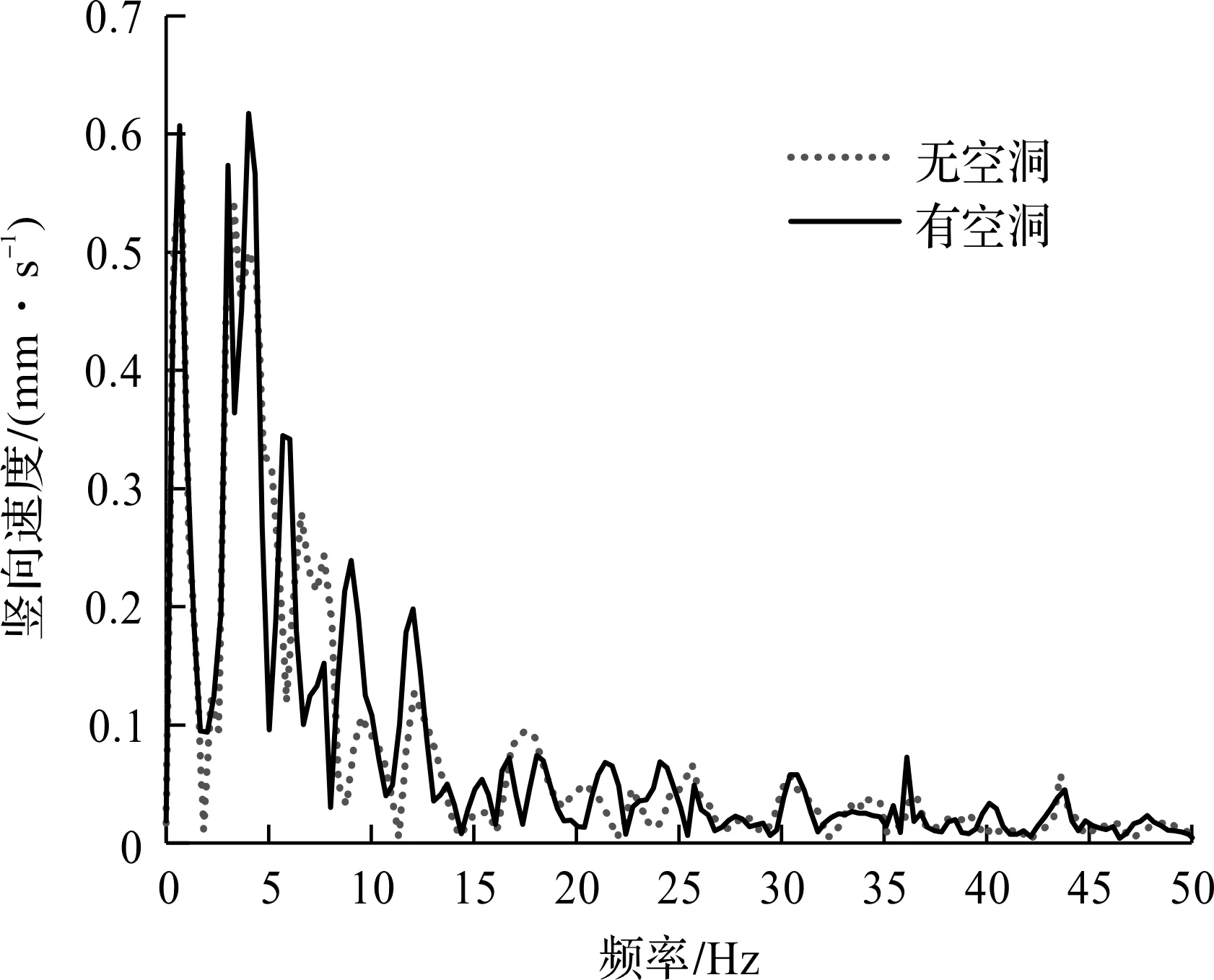
图10 道路板竖向速度的频谱曲线Fig.10 Spectrum of vertical velocity of road slab

3.2 模态分析

利用Lanczos求解器对有无路基空洞的模型进行模态分析,获得了两个模型在20 Hz以内的特征频率及其模态云图。应注意,路基是典型的模态密集对象,模态阶数极多。考虑到车辆的移动轴加载频率f=v/l=3.06 Hz(其中,v为车速;l为前、后轮轴距),该频率与图9,10中的峰值频率3.01 Hz相符,因此特别关注了3 Hz以内的模态信息,特征频率如表3所示。

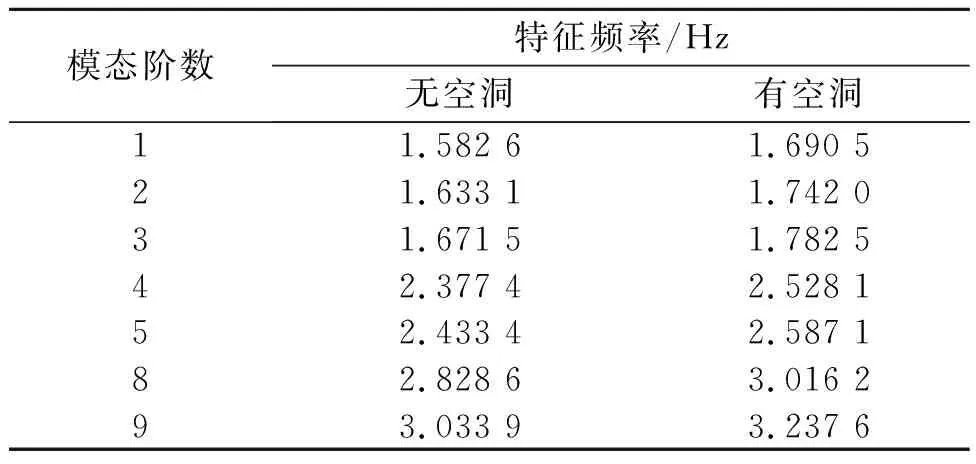
表3 特征频率对比表

图11对比了第8阶模态云图。由图11可知:虽然路基存在空洞和无空洞时的模态相似,均在道路板中点位置出现位移峰值,但是路基存在空洞时的特征频率为3.016 2 Hz,略高于无空洞模型的2.828 6 Hz。

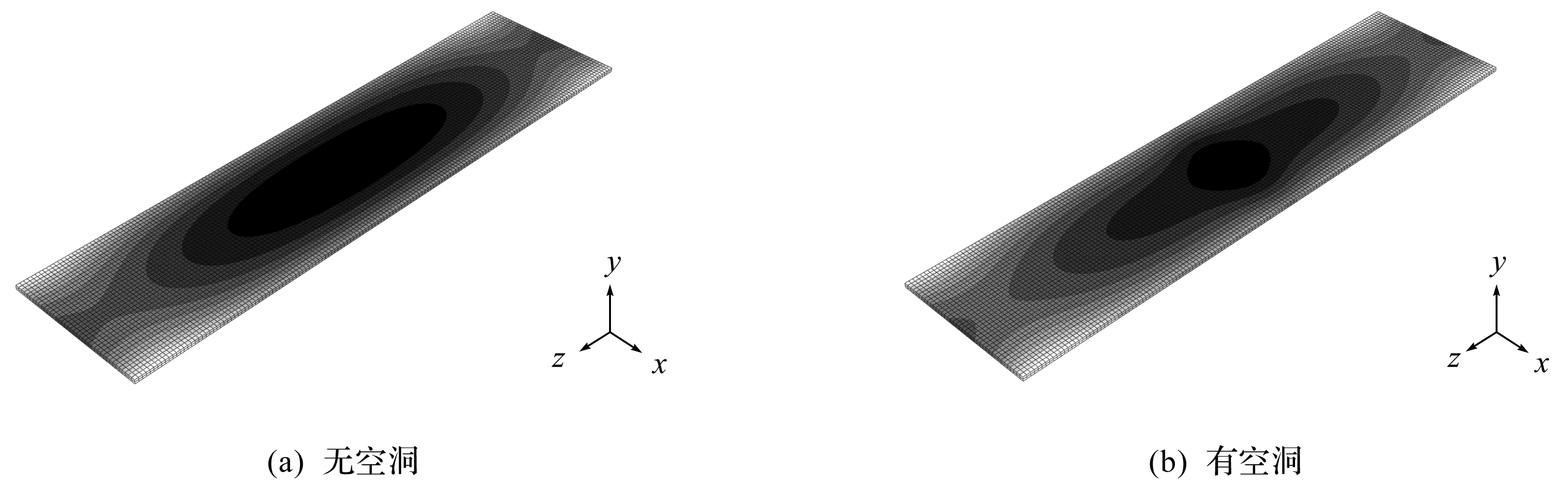
图11 同阶模态云图Fig.11 Cloud images of the same modal

当特征频率相同时,两模型的模态云图不同。选取图9,10中峰值频率3.0 Hz附近的模型特征频率——无空洞模型的3.033 9 Hz和有空洞模型的3.016 2 Hz(表3),对应的模态云图如图12所示。由图12可知:二者差异明显,当路基无空洞时,振动位移峰值出现在板端;当路基存在空洞时,振动位移峰值位于板中心。

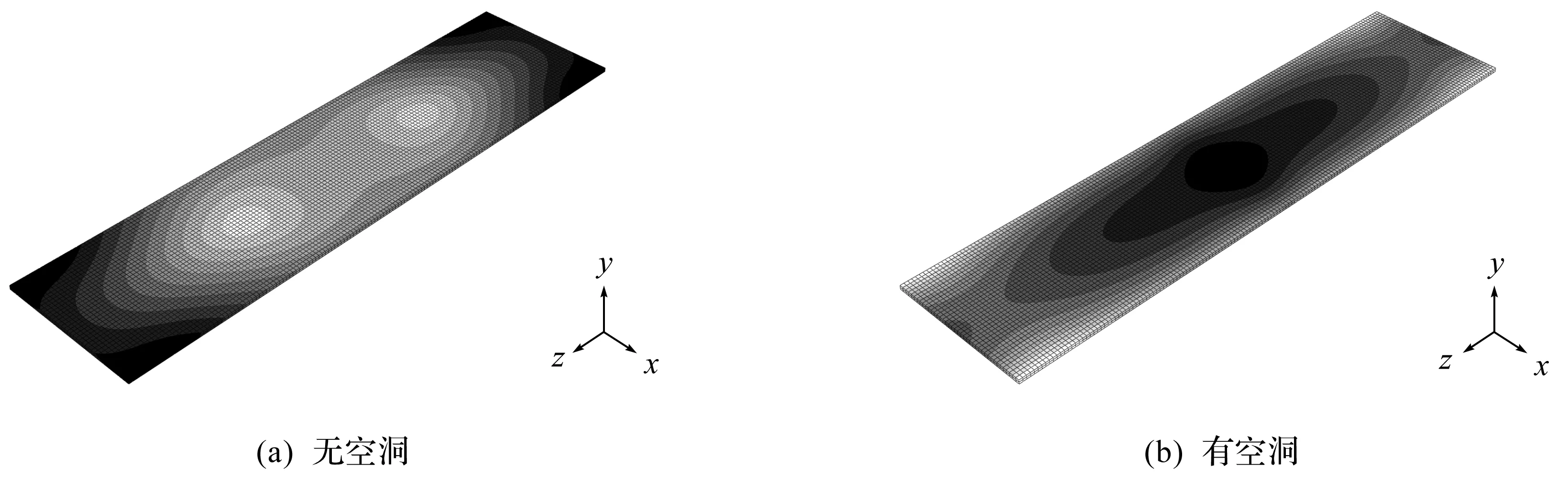
图12 3.0 Hz附近模态云图对比Fig.12 Comparison of modal cloud images of the two models at 3.0 Hz

3.3 稳态分析

利用ABAQUS的稳态分析功能,在特征频率附近进行扫频,获得稳态加载下道路板的位移和速度响应曲线。图13,14分别呈现了观察点的稳态位移与速度响应曲线,频率范围6 Hz约包含前50阶模态。由图13,14可知:路基空洞会引起响应峰值增加,且峰值所对应的频率(峰值频率)增大约0.3 Hz,与3.1节和3.2节结论相符。空洞虽然会导致路基质量与刚度减少,但其质量减少幅度更大,因此导致了峰值频率向高偏移现象。

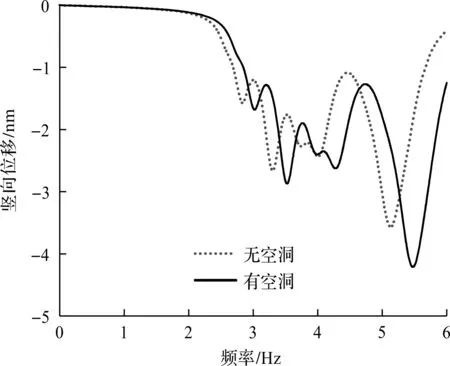
图13 稳态分析的位移曲线Fig.13 Displacement response from steady-state analysis

4 道路板与土相对模量影响

通过设置不同的道路板与路基土模量比(Ec/E=300,600,1 200)来探究道路板和路基土体刚度变化对振动特性的可能影响,其他模型参数设置与前述相同。以模量比Ec/E为横坐标,以有无路基空洞时的道路板峰值位移和峰值速度的比值为纵坐标,分别绘制图15,16。由图15可知:当模量比Ec/E=300和600时,道路板位移峰值比值十分接近。然而当Ec/E增大至1 200时(例如软土地基上覆刚性道路板),无空洞时的道路板位移峰值仅为有空洞时的一半,即道路板位移峰值对路基空洞的存在变得更加敏感。由图16可知峰值振速比随着模量比Ec/E的增加而逐渐减小。特别是当Ec/E=300时,无路基空洞时的道路板峰值振速高于有空洞情形。相较于峰值振速而言,峰值位移比对模量比的变化相对不敏感,其比值变化范围[0.52,0.64]也相对较小。

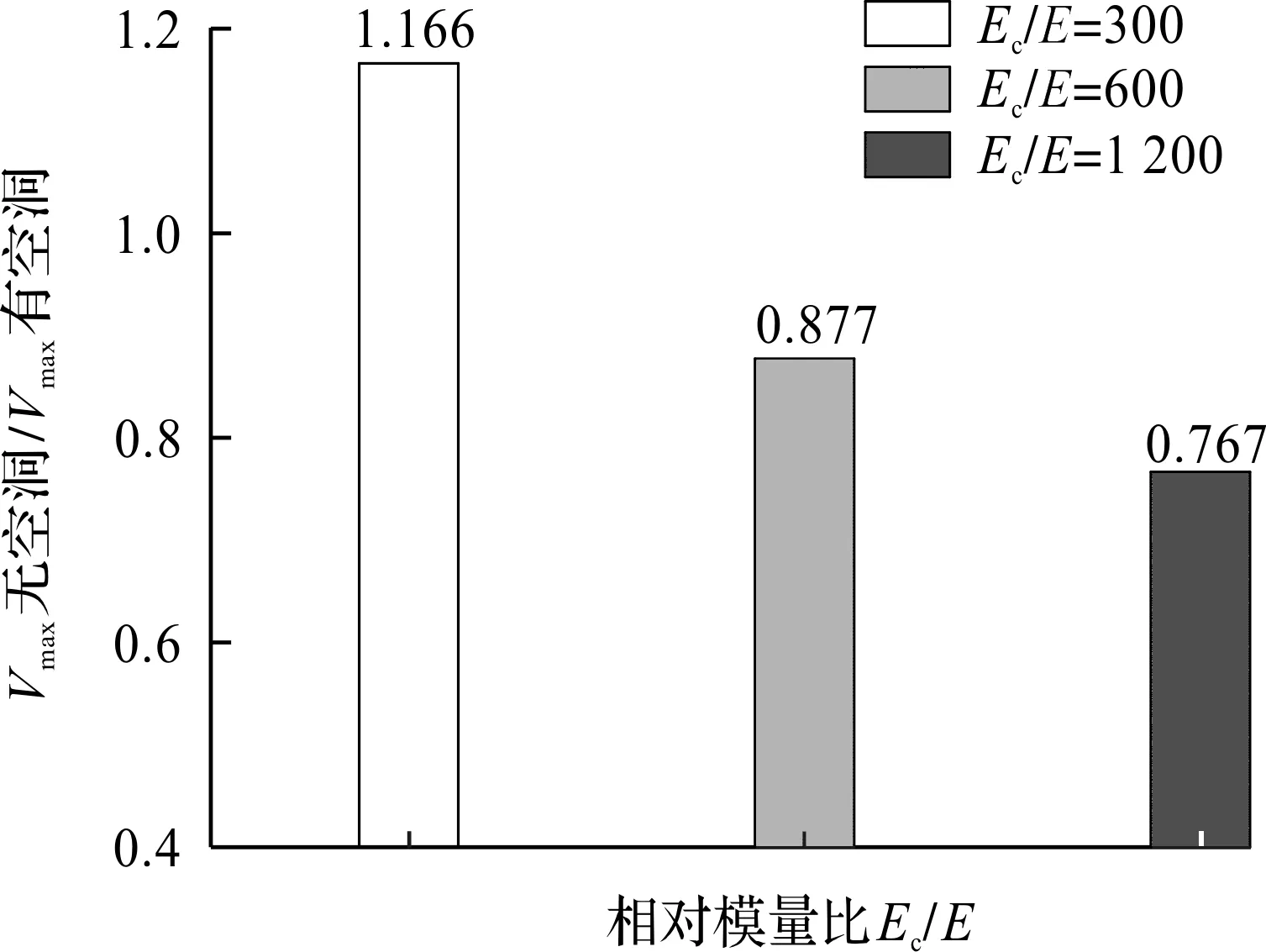
图16 相对模量比对道路板振动速度峰值比的影响Fig.16 Influence of relative modulus ratio on maximumvibrational displacement ratio

针对有空洞的路基模型,取不同模量比Ec/E下的道路板中点竖向位移和速度时程进行快速傅里叶变换获得振动响应频谱,如图17所示。由图17可知:2 Hz附近的峰值频率虽然随着Ec/E的增大而逐渐向左偏移,但是偏移量较小,说明道路板和路基刚度变化对峰值频率影响不大。

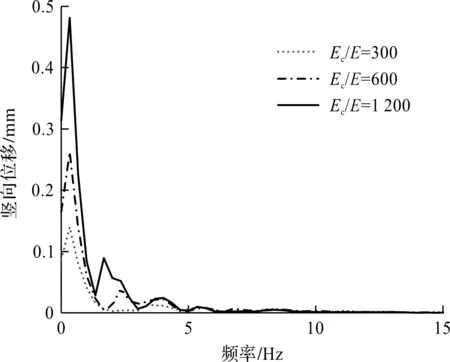
图17 竖向位移的频谱曲线(有空洞)Fig.17 Spectrum of vertical displacement (with cavity)

5 路基空洞尺寸影响

路基空洞可能不断发育扩大,当扩大至路基表面时则容易造成路板塌陷。因此,有必要探究路基空洞的尺寸对道路板振动的影响。针对图1所示的“大洞”,施加图4相同的车辆荷载,可获得道路板观察点的时频响应特性,如图18～20所示。由图18可知:空洞体积增加会引起道路板峰值位移的进一步放大。由图19可知:“大洞”在4.01,6.69,9.03 Hz等频率处的响应要明显高于“小洞”,说明“大洞”会明显降低路基刚度。由于“大洞”在引起路基刚度下降的同时也减小了路基参振质量,两者对峰值频率的影响相互补偿,稳态分析中“大洞”与“小洞”的峰值频率偏移程度相当,如图20所示。

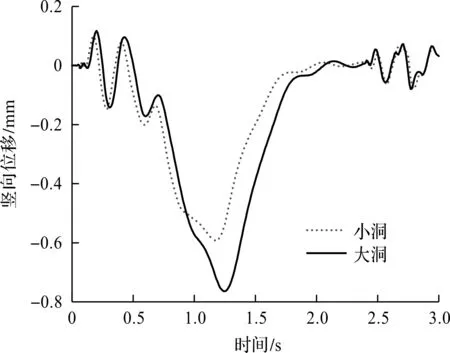
图18 路基空洞尺寸对振动位移的影响Fig.18 Influence of underground cavity sizeon vibration displacement

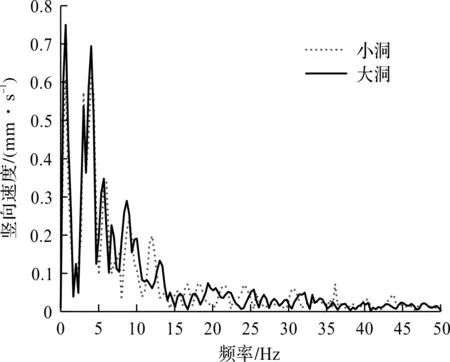
图19 竖向速度的频谱曲线Fig.19 Spectrum curve of vertical velocity

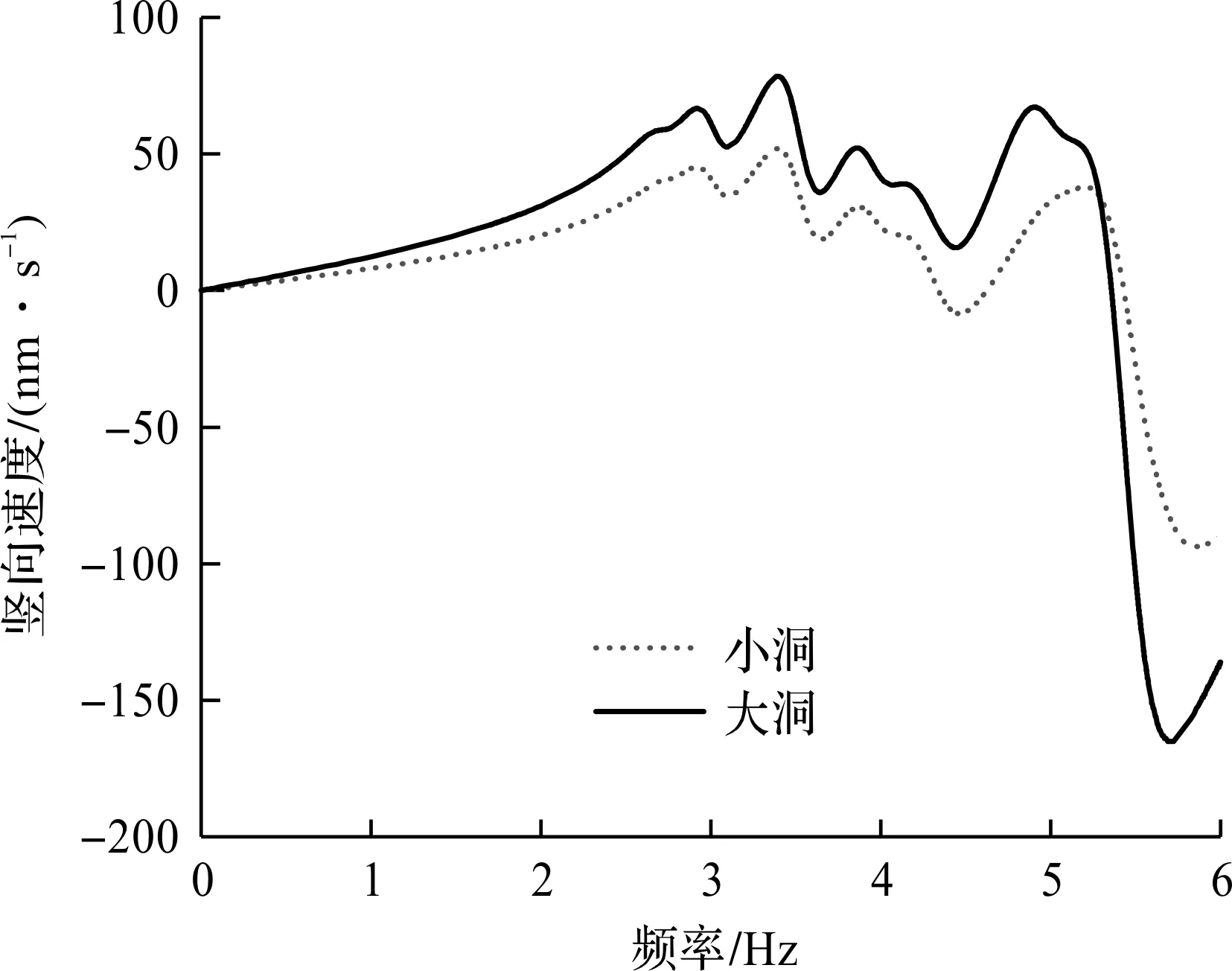
图20 不同空洞尺寸下稳态分析的速度曲线Fig.20 Velocity curves for steady-state analysis ofdifferent cavity sizes

6 结 论

在有限元软件ABAQUS中分别建立了无空洞和有空洞的三维混凝土道路板—软土路基耦合振动分析模型,利用车路耦合单元(VRI)施加移动车辆荷载,获得了道路板振动位移和速度时程曲线。同时,利用快速傅里叶变换,获得了道路板振动位移和速度频谱,并结合模态和稳态扫频分析研究了路基空洞对道路板速度谱和道路板—路基体系峰值频率的影响规律,考虑了不同空洞几何尺寸以及道路板/路基模量比值条件的影响,得出如下结论:1) 路基空洞会放大道路板振动位移峰值,且位移峰值随着空洞尺寸的增加而增大;2) 当单一移动车辆荷载通过时,虽然道路板振动速度时程曲线受空洞影响较小,但是能观察到速度频谱有明显的峰值频率偏移;3) 当道路板—路基体系发生稳态振动时,路基空洞会明显增大其峰值频率;4) 两模型峰值振速比随着道路板与路基土模量比Ec/E的增加而减小,而峰值位移、峰值频率受其影响不明显。