基于BiLSTM的基坑开挖贝叶斯更新方法

李贺勇,许高波,李世俊,何炳罕,虞梦菲

(1.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 310014;2.浙江华东工程咨询有限公司,浙江 杭州 311122; 3.浙江省岱山经济开发区环城投资集团有限公司,浙江 舟山 316212;4.浙江工业大学 土木工程学院,浙江 杭州 310023)

笔者提出一种基于双向长短时记忆(BiLSTM)神经网络的高效贝叶斯更新方法。首先,利用既有开挖阶段的多点墙体侧移监测数据,基于多重集合卡尔曼滤波方法(EnKF-MDA)更新关键土体参数,提高预测的准确性;然后,构建BiLSTM代理模型替代贝叶斯更新方法中的原始有限元模型,提高贝叶斯更新的计算效率;最后,以台北TNEC基坑为例,将笔者方法应用到工程实例中,将预测结果与实测值进行对比分析,验证笔者方法的有效性和准确性。

1 基于BiLSTM和EnKF-MDA的基坑开挖侧移预测方法

笔者方法主要包括两个部分:1) 基于有限元模拟数据构建BiLSTM模型;2) 将BiLSTM模型作为贝叶斯框架中的计算模型,基于EnKF-MDA结合既有监测数据更新关键土体参数,利用更新后的土体参数预测后续开挖阶段的基坑变形响应。下面分别介绍BiLSTM模型、EnKF-MDA算法和笔者方法的具体步骤。

1.1 双向长短时记忆神经网络

为缓解传统循环神经网络(RNN)梯度消失的问题,1997年Hochreiter等[8]提出长短时记忆神经网络(LSTM),专门设计具有记忆能力的神经元替换传统循环神经网络中的神经元节点,其主要由遗忘门、输入门和输出门等结构组成。由于门结构的存在,LSTM具备选择性记忆的功能,可以有选择地关注重要信息,过滤掉无关信息。这个功能主要用σ来实现,σ即sigmoid函数,取值是0～1,代表信息通过的比例。取0时,模型认为信息不重要,选择遗忘;取1时,模型认为信息很有价值,选择记忆。LSTM单元内部结构如图1所示。图1中:⊗代表点积运算;⊕代表求和运算。计算公式表示如式(1～6)。

(1)

(2)

it=σ(Wi[ht-1,xt]+bi)

(3)

(4)

ot=σ(Wo[ht-1,xt]+bo)

(5)

ht=ottanh(Ct)

(6)

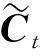
BiLSTM在LSTM的基础上同时考虑了前向和后向的信息进行预测,实现双向序列信息的利用,通常用于前向信息和后向信息同样重要的场景,如机器翻译。采用BiLSTM作为代理模型替代有限元模型作为贝叶斯更新中的正向计算模型,具有以下优点:1) 与原始有限元模型相比,BiLSTM神经网络计算快速,减少了贝叶斯更新过程中多次调用计算模型的计算用时;2) 与传统基于多项式的代理模型相比,BiLSTM的输出是沿墙体深度的多点侧移构成的向量,而不是各个观测点的单一数值,所需要的代理模型数量显著减少;3) BiLSTM可以考虑前后空间序列信息,更符合墙体侧移实际情况。

1.2 基于多重数据融合的集合卡尔曼滤波方法

集合卡尔曼滤波(EnKF)是传统卡尔曼滤波(KF)的非线性变体,在KF的基础上加入“集合”预测的概念。传统卡尔曼滤波采用误差协方差递推方程计算误差协方差矩阵,而集合卡尔曼滤波通过一组集合样本计算得到误差协方差矩阵[9],更适用于岩土工程非线性模型。基于多重数据融合的集合卡尔曼滤波方法(EnKF-MDA)是对EnKF的进一步改进,采用迭代形式结合观测数据并放大单次观测误差,进一步提高了强非线性问题处理能力。EnKF-MDA的计算步骤如下:

1) 初始步。根据收集的资料(地质勘察报告、文献等)和工程经验,确定土体参数的先验分布,通过随机抽样算法生成土体参数样本xj(j=1,2,…,M),构成初始集合。

2) 预测步。将初始集合(或上一迭代步i-1得到的更新集合)代入BiLSTM计算模型,获得下一迭代步i的基坑侧移预测值y,计算式为

2.1.1 充分利用草山资源根据草山面积，决定养殖规模，既不能过度放牧，造成草山资源枯竭，甚至水土流失；又要充分利用草山资源，以达到效益最高化。

(7)

式中:函数H(·)为BiLSTM计算模型;下标i为迭代步;下标j为样本号。同理,“预测”迭代步i的土体参数计算式为

(8)

式中:迭代步i的土体参数预测值取为上一迭代步i-1的更新值;上标f和a分别为预测和更新。

基于集合中的样本,计算土体参数与观测量的互协方差矩阵Dxy以及观测量的自协方差矩阵Dyy,计算式分别为

(9)

(10)

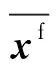
3) 更新步。卡尔曼增益矩阵K和结合实际观测数据来更新土体参数的计算式分别为

Ki=Dxy,i(Dyy,i+aiR)-1

(11)

(12)

式中:d为实际观测数据;ε为观测误差,服从均值为0、协方差为R的高斯分布;ai为EnKF-MDA中观测误差的放大系数。针对基坑开挖某一阶段的监测数据,交替进行预测步和更新步Nmda次,可简单取Nmda等于ai。

1.3 基坑开挖侧移预测方法流程

笔者提出的基坑开挖侧移预测方法的流程图如图2所示,主要分为构建BiLSTM和基于EnKF-MDA的贝叶斯更新两部分。在构建BiLSTM中,首先,确定土体参数的取值范围,利用拉丁超立方抽样随机生成一定数量的土体参数样本,针对研究的基坑项目,建立对应的有限元模型,将这些土体参数样本输入有限元模型,计算得到基坑各开挖阶段的墙体侧移数据集;然后,将数据集随机划分为两个部分,80%的数据用于训练,剩余20%用于测试;最后,调整模型超参数,构建各阶段对应的BiLSTM代理模型,替代原始有限元模型。在基于EnKF-MDA的贝叶斯更新中,首先,基于土体参数的先验分布,生成土体参数的初始集合;然后,将其代入BiLSTM模型,计算得到基坑开挖阶段n的侧移预测值,构成预测集合,将侧移预测值与该开挖阶段n的观测数据进行对比,根据式(12)更新土体参数,得到参数更新集合;最后,交替进行预测步和更新步Nmda次,得到结合基坑开挖阶段n的监测数据后的土体参数更新值。采用更新的土体参数预测后续开挖阶段n+1的侧移响应,随着施工的进行,获得开挖阶段n+1的监测数据后,以上一阶段更新的土体参数为本阶段土体参数的先验分布,同理重复更新过程,逐步结合各阶段监测数据。

2 台北TNEC基坑开挖算例分析

2.1 算例介绍

以台北TNEC基坑开挖为例来评估笔者所提出的基坑开挖墙体侧移预测方法的有效性。通过收集整理现有的文献[10-13]可以获得此案例的施工顺序、土工试验数据和现场监测数据等信息,场地土层中软黏土层和砂土层交替出现,基坑开挖宽度和深度分别为41.2 m和19.7 m,地下连续墙厚度为0.9 m,采用明挖法自上而下进行施工,整个开挖过程分为7个阶段,具体如图3所示。

有限元模型示意图如图4所示。在建立有限元模型时,根据基坑几何对称性,只分析项目的一半,基坑开挖宽度为20.6 m。为了尽量减少边界对基坑开挖模拟的影响,有限元模型宽度设为100 m,超出基坑开挖的影响区,模型深度设为46 m。左边界固定水平和旋转自由度,右边界固定水平自由度,底部固定水平和垂直自由度。黏土层用修正剑桥模型进行模拟,砂土层用摩尔库伦模型进行模拟[12],土体参数如表1,2所示。未知的土体参数是压缩参数λ、回弹参数κ、临界状态应力比M、泊松比υ,其上下限根据黏土的典型范围确定[10,13]。表1,2中:H为深度,r为土的重度,c为黏聚力,φ′为内摩擦角,ψ为剪胀角,E为弹性模量,K0为静止土压力系数,e0为初始孔隙比。

图4 有限元模型示意图Fig.4 Schematic diagram of the finite element model

表2 TNEC黏土层的土体参数

2.2 BiLSTM模型构建

使用ABAQUS软件建立有限元模型,通过拉丁超立方抽样在表2给定的范围内随机生成2 000组土体参数,并进行相应的有限元计算来准备BiLSTM模型训练和测试所需的数据集。每组样本的输入为12个土体参数(3个黏土层各自的κ,M,υ,λ)的随机样本,输出是基坑一挡土墙截面不同深度处的墙体侧移。

BiLSTM和有限元模型在测试集上计算的墙体侧移的比较情况如图5所示。当监测点间隔为2 m,即监测点数量为17时,BiLSTM模型计算结果和有限元模型计算结果吻合较好,平均绝对误差为0.45 mm,说明BiLSTM可精准替代原始有限元模型。

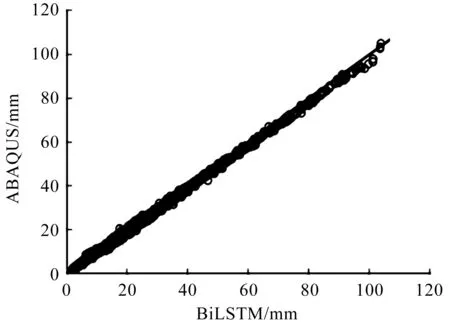
图5 BiLSTM和有限元模型在测试集上计算的墙体侧移的比较Fig.5 Comparison of wall deflections calculated by BiLSTMand finite element model on the test set

2.3 土体参数先验分布和后验分布

在贝叶斯框架中,需要确定土体参数的先验信息,以往文献的敏感性分析[14]显示土体参数λ1,κ1,υ1,M1,κ2,υ2,υ3有较高的敏感性,取这7个参数为待更新的土体参数,其先验分布的均值取表3中的可能范围的中间值,变异系数均取30%。为了保证土体参数是非负的,假定这些参数是对数正态随机变量。由于基坑开挖初期的变形模式与后续阶段不同[15],对土体参数的更新从第3阶段开始。敏感性分析[14]显示,参数υ2,κ2敏感性显著高于其他参数,故图6以参数υ2和κ2为例,对比了土体参数的先验分布和结合第3阶段观测数据之后的后验分布。参数υ2和κ2后验分布变异系数分别为6.5%和24.6%,均低于先验分布的变异系数30%。由图6可知:参数υ2和κ2的后验概率密度函数明显比先验分布更为集中,土体参数不确定性显著降低。

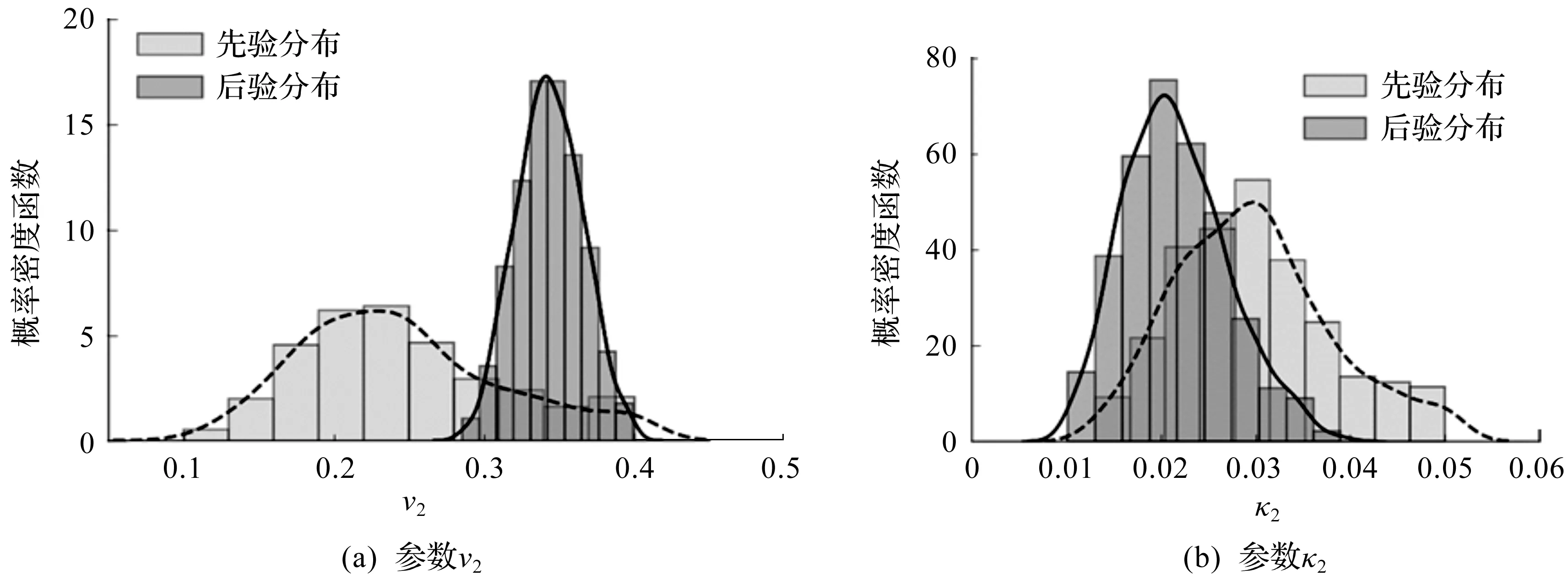
图6 土体参数的先验和后验分布Fig.6 Priori and posteriori distribution of soil parameters

2.4 墙体侧移预测结果

将每个阶段更新得到的土体参数代入BiLSTM模型得到该阶段的墙体侧移的预测结果,和现场观测结果进行比较,结果如图7所示。图7中:虚线表示先验估计的均值;实线表示预测的平均值;误差条表示2倍标准差。由图7可知:使用土体参数先验分布显著低估了基坑开挖的侧移,且低估程度随着基坑开挖的进行逐渐扩大。而笔者方法可有效结合各阶段的监测数据,不断更新土体参数,使用更新的土体参数可以得到比先验分布更准确的预测结果。

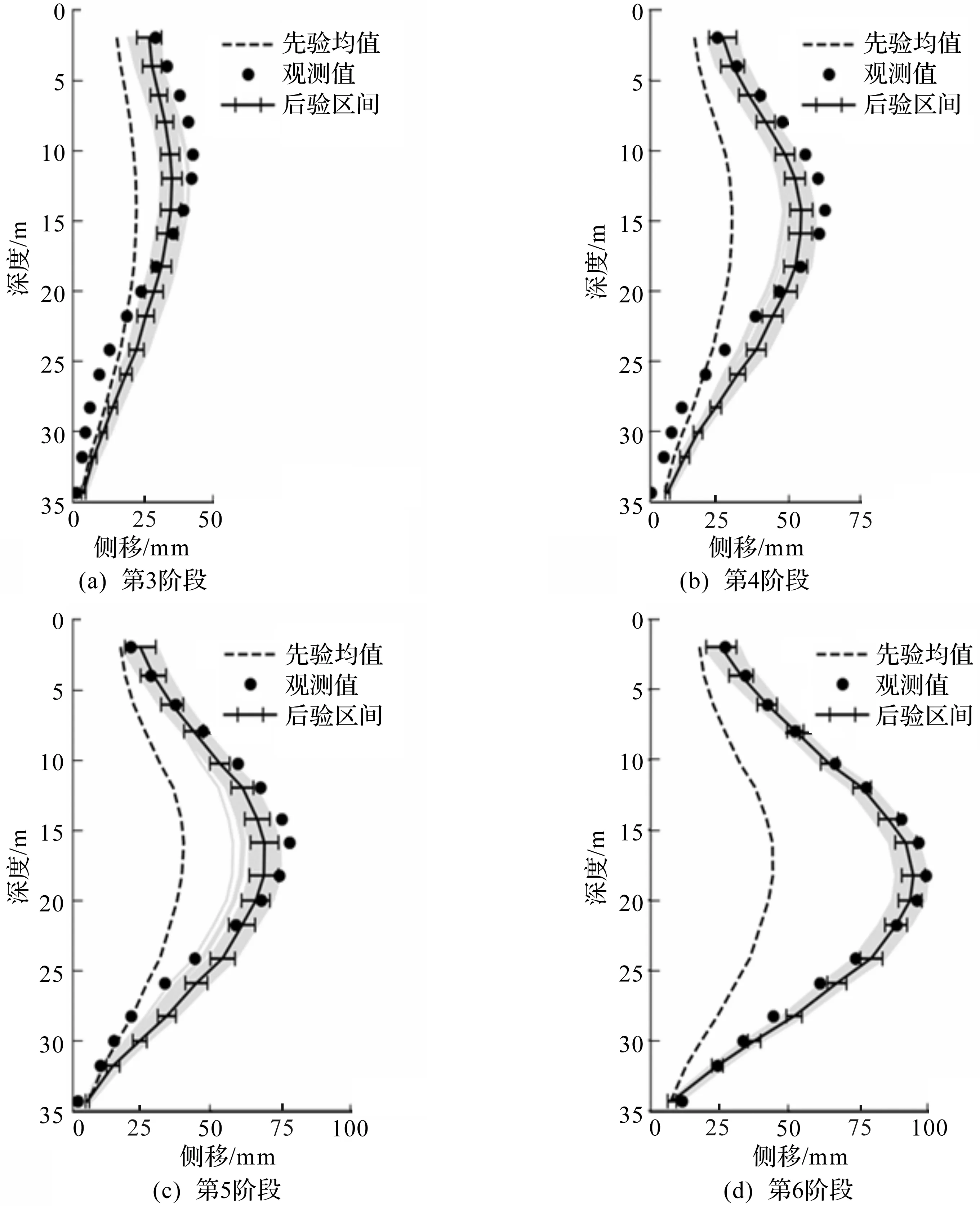
图7 基坑开挖各阶段侧移估计值Fig.7 Estimated values of wall lateral shifts in different excavation stages

使用上一阶段监测数据更新后的土体参数对下一开挖阶段墙体侧移进行预测,具体情况如图8所示。图8(a)显示了利用第3阶段的观测数据,更新土体参数,并采用更新后的土体参数预测第4阶段的侧移。由图8可知:虽然基于上一开挖阶段更新得到的土体参数略微低估了当前基坑开挖的最大墙体侧移,预测值和观测值的差异略大于图7中后验估计值与观测值的差异,但是显著优于图7中基于先验分布的计算结果。随着基坑开挖的进行,结合监测数据的增多,预测的均值显著向现场观测值靠拢。在第7阶段,预测均值与实测值吻合程度高,预测的95%置信区间基本覆盖了实测值。

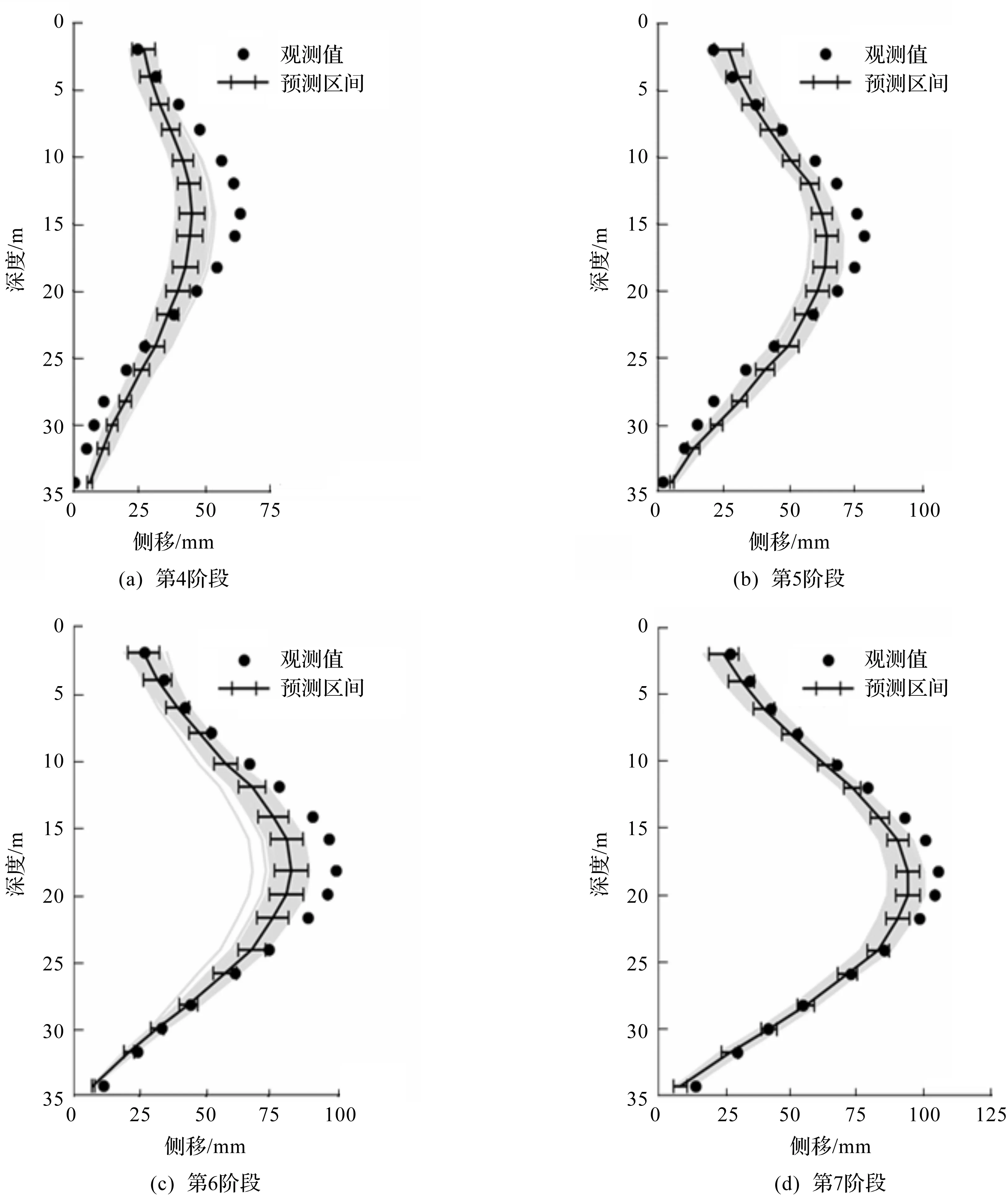
图8 基坑开挖各阶段侧移预测值Fig.8 Predicted values of wall lateral shifts in different excavation stages

3 结 论

提出了一种基坑开挖贝叶斯更新与侧移预测方法,基于EnKF-MDA动态融合多阶段多位置基坑监测数据,构建BiLSTM代理模型以提高贝叶斯更新的计算效率,实现了土体参数的高效更新。以台北TNEC基坑开挖项目为例说明和验证笔者方法。结果表明:BiLSTM可以学习土体参数和基坑侧移间的非线性映射关系,精准替代原始有限元模型。笔者方法可有效结合多阶段多位置侧移监测数据,提高基坑变形预测准确度。在实际应用中,一旦获得当前阶段的监测数据,就可以快速更新和预测后续阶段的基坑变形,当基坑变形较大时,可及时采取相应的措施,降低基坑开挖工程的施工安全风险。