考虑目标偏好的应急物资调度方案优化方法

汪 勇，李文凯，艾学轶，蒲秋梅

（1.武汉科技大学 恒大管理学院，武汉 430065；2.中央民族大学 信息工程学院，北京 100081）

0 引言

应急物资调度（Emergency Material Scheduling，EMS）的研究主要包括调度模型和求解方法两个方面。Hu 等（2019）[1]指出EMS 调度模型主要以最短时间、最短距离、最小成本、最大满意度、公平性等为目标。Liu 等（2021）[2]考虑到受灾群众满意度，建立了具有满意度约束的调度模型。L（i2021）[3]建立了考虑运输时间、成本、资源可用性等影响因素的资源调度模型。薛星群等（2020）[4]以受灾点等待救援的平均时间最短以及应急网络总费用最低为目标，构建运力受限条件下受通行约束的救援物资联合运输多目标优化模型。苑津莎等（2020）[5]在考虑需求点满意度的同时，引入需求迫切度概念，进一步提高调度模型的科学性。Wan等（2021）[6]建立了基于有序到货原则的多目标多约束应急物资调度模型。由于灾害发生后，很难估计应急救援物资的需求，刘扬等（2019）[7]以三角模糊数描述物资需求的不确定性，构建了考虑需求点匹配度和响应时间的多目标调度模型。Liu 等（2020）[8]提出了一个具有连续时变供需约束的应急物资分配多目标优化模型，使得应急救援行动的损失和经济成本最小化。

EMS 因其多目标和多约束特性在大多数情况下为强NP-Hard问题，启发式算法成为解决这类优化问题的重要方法。但启发式算法几乎都存在早收敛和优化精度不高的问题，为此，一些改进和融合算法有效地改善了算法的性能。Han等（2021）[9]通过引入状态转移算法的四种状态变换算子，解决了模拟退火算法探索初期收敛进度慢的问题。Joshi 等（2021）[10]提出了一种嵌入邻域档案的改进引力搜索算法，有助于以更少的时间复杂度增加多样化的搜索。Mohammed 和Rashid（2020）[11]提出鲸鱼灰狼优化算法，解决了局部搜索能力不足的问题。

目前，考虑目标偏好的多目标应急物资调度研究尚不多见，算法的优化精度和搜索性能仍值得进一步改善，鉴于此，本文建立一个具有目标偏好的双目标应急物资调度模型，提出一种麦田竞赛算法（Tournament in Cornfield Algorithm，TCA），以解决EMS方案优化问题。

1 应急物资调度模型

1.1 假设条件

受到物资储备量、道路状况、运输能力等因素的影响，使得应急物资调度成为一项十分复杂的优化问题。考虑到上述影响因素以及应急物资调度的可行性，对调度模型作如下假设：（1）供应点是指第三方商业性物资储备库。（2）各类物资总储备量大于总需求量。（3）每个需求点应急物资需求和每个供应点应急物资储备的种类和数量不完全相同。（4）每个需求点可以从多个供应点调度物资，每个供应点可以向多个需求点供应物资。（5）同一供应点运输车辆性能相同且数量有限，每辆车只从一个供应点装载物资，只为一个需求点运送物资。

1.2 调度模型构建

1.2.1 问题描述

设有n个需求点，m个供应点，u种应急物资，qik表示需求点i需求应急物资k的数量，cjk表示供应点j储备应急物资k的数量。一个调度方案x可表示为x={xijk|i=1，2，…，n，j=1，2，…，m，k=1，2，…，u}。为减少灾害带来的损失，在最短时间内将应急物资配送到位是调度者首要考虑的目标。此外，由于供应点是商业性物资储备库，因此在保障应急物资及时供给时，需考虑应急物资的采购成本。故以时间和成本为目标构建应急物资调度模型。f1(x)、f2(x)分别表示调度时间和调度成本，调度目标是使得f1(x)与f2(x)最小，即：

式（2）至式（7）为式（1）的约束条件。式（2）表示应急物资调度数量整数约束，即决策变量xijk为正整数。式（3）表示决策变量xijk非负且不大于供应点j物资k的储备量。式（4）表示所有需求点从供应点j调度物资k的总量不大于该供应点物资k的储备量。式（5）表示需求点i从所有供应点调度物资k的总量等于该需求点对物资k的需求量。

式（4）、式（5）是决策变量定义域约束。所有决策变量定义域不相同且存在依赖关系。由式（4）知，当供应点j可供调度的物资k数量小于需求点i需求物资k的数量时，则需求点i从供应点j调度物资k的数量不超过该供应点剩余物资k的数量。即

由式（5）知，需求点i从供应点j调度物资k的数量不超过该需求点所需剩余物资k的数量，即xijk≤qik-

式（6）表示供应点物资储备量和需求点物资需求量非负约束。式（7）表示所有需求点物资k的需求量不超过所有供应点物资k的储备量。

1.2.2 调度时间

在不考虑物资装载时间的情形下，调度时间即应急物资运输时间。每个供应点按照需求点受灾程度运送应急物资，先向受灾程度最严重的需求点运送物资，接着向受灾程度次严重的需求点运送物资，依此类推，直到完成所有需求点的物资运送任务。对于一个调度方案x，设需求点i从供应点j调度物资总重量为Mij(x)，则：

其中，rjk是供应点j物资k的储备状态，cjk=0 时，rjk=0；cjk＞0 时，rjk=1。wjk是供应点j物资k的单位重量。设供应点j向所有需求点运送物资的车次为b(j)，则：

其中，gj是供应点j车辆载重量。b(j)≠0 时，表示需要多台车辆运送应急物资。设供应点j总的运输任务为Sj(x)，根据式（8）、式（9），Sj(x)={s1，s2，…，sb(j)}，b(j)为运输任务数，即每车次为一个运输任务。一个需求点可能存在多个运输任务，供应点j到需求点i的运输时间记为Tij(x)，则：

其中，dij是供应点j到需求点i的距离，vj是供应点j车辆平均时速。由式（10）可得各任务的运输时间Tj(x)={t1，t2，…，tb(j)}。设供应点j的车辆数为h(j)。根据运输任务及其运输时间计算供应点j的调度时间DTj(x)。0时刻开始执行前h(j)个运输任务，当有运输任务完成时，释放的车辆开始执行第h(j)+1个运输任务，依此类推，直到所有运输任务完成为止，设第a(a=1，2，…，b(j)-h(j)+1)批任务最短运输时间为STa，则第a+1批任务的剩余运输时间RTa+1见式（11）。

显然，a=1 时，RT1∈{t1，t2，…，th(j)}。根据式（11）计算每一批未完成任务的剩余运输时间，从而得到该批任务的最短运输时间STa和最后一批任务的最长运输时间LTb(j)-h(j)+1，则所有任务的调度时间见式（12）。

总的调度时间f1(x)取决于所有需求点调度时间的最大值，即：

其中，μ为惩罚因子。若调度方案满足式（3）、式（4）约束，则μ=1，否则，μ=+∞。

1.2.3 调度成本

调度成本由采购成本和物流成本构成。由假设条件可知，供应点为商业性物资储备库，调度物资必然产生成本，称为采购成本，记为pc(x)。采购成本取决于供应点应急物资单位价格和调度数量。设pjk表示供应点j应急物资k的单位价格，则所有需求点调度的应急物资采购成本为：

其中，xijk=0 表示需求点i没有应急物资k的需求。

物流成本主要来自车辆使用费，记为lc(x)。设ρj表示供应点j的单位运输费用。根据式（8）得到物流成本为：

由式（14）和式（15）得到调度方案x的调度成本为：

1.3 调度方案编码

由于直接采用优化变量实值编码易产生大量无效解，故设置一个新的决策变量ωijk，ωijk∈[0，λ]，λ为所有新的决策变量上界。ωijk表示需求点i从供应点j调度应急物资k的份额，ωijk是一个三维变量，为便于计算，按照需求点排列为一维结构编码。新变量与原始变量的映射函数见式（17）。

2 麦田竞赛算法

2.1 相关定义

定义1：选手手中的麦穗称为标准麦穗，标准麦穗的集合称为标准群体，记为X，X={xi|i=1，2，…，N}，xi表示第i个标准麦穗。选手眼中搜寻到的麦穗称为挑战麦穗，挑战麦穗的集合称为挑战群体，记为Y，Y={yi|i=1，2，…，N}，yi是xi的挑战麦穗。N为群体规模。

定义2：决策变量是一组反映麦穗质量的物理指标。xij表示标准麦穗xi的第j项物理指标，j=1，2，…，L。yij表示挑战麦穗yi的第j项物理指标。L为物理指标数。

定义3：筛选目标是判断标准麦穗和挑战麦穗质量优劣的依据，如颗粒饱满度、色泽等。筛选目标与麦穗物理指标间的关系称为筛选目标函数，记为fk(xi)，fk(xi)表示标准麦穗xi的第k个筛选目标，k=1，2，…，m，m为目标数。选手关注程度最高的目标称为偏好目标。

定义4：设xi∈X，yi∈Y，xi与yi具有质量优劣关系，若∀k∈[1，m]，都有fk(yi)≥fk(xi)成立，则yi优于xi，yi为优等麦穗，记为yi≻xi。反之，xi为优等麦穗，记为xi≻yi。显然，麦穗质量优劣关系具有传递性。若xi，xj，xh∈X，xi≻xj，且xj≻xh，则xi≻xh。

定义5：对于xi∈X，yi∈Y，若∃k，l∈[1，m]，k≠l，使得fk(xi)＞fk(yi)，且f1(xi)＜f1(yi)，则称xi与yi质量不具有优劣关系，即不存在xi≻yi，也不存在yi≻xi，记作xi≺≻yi。

定义6：反映麦穗xi成熟程度的函数称为成熟度函数，记为F(xi)。设xi，xj∈X，i，j=1，2，…，N，若xi≻xj，则F(xi)=1，F(xj)=-1。反之，F(xi)=-1，F(xj)=1。若xi≺≻xj，则F(xi)=F(xj)=0。

定义7：设xi∈X，若对于∀xj∈X，k∈[1，m]，都有F(xi)＞F(xj)成立，则称xi为标准麦穗群体的最优麦穗。若对于∀xj∈X，都有Fk(xi)＞Fk(xj)成立(k=1，2，…，m)，则称xi为偏好目标k的最优麦穗。

2.2 麦穗搜寻阶段

TCA主要包括麦穗搜寻和麦穗筛选两个阶段，搜寻实际上是标准麦穗的启发式计算过程，由此产生挑战麦穗。搜寻阶段从当前标准群体出发，竞赛选手根据标准麦穗所在的区域范围，搜寻标准麦穗附近的挑战麦穗，所有选手搜寻到的挑战麦穗构成挑战群体。

设xij(t)表示第t轮标准麦穗xi的第j个物理指标，yij(t)表示其挑战麦穗相应的物理指标，i=1，2，…，N，j=1，2，…，L。根据定义2，挑战麦穗yi(t) 与标准麦穗xij(t)的启发式计算见式（18）。

式（18）中，Dij(t)是t轮标准麦穗xi物理指标j的搜寻方向。当标准个体与挑战个体的指标值（决策变量）与成熟度值变化趋势一致时，Dij(t)=1，相反时，Dij(t)=-1；当指标值无变化时，Dij(t)保持不变。搜寻方向引导算法朝着最优解方向定向搜索，进一步提升TCA 的搜索性能。Instij是物理指标j的搜寻指令，Instij=0 表示停止搜寻，Instij=1表示开始搜寻。vij是物理指标j的搜寻速度，vij计算见式（19）。

式（19）中，r是均值为0、方差为1的正态分布的随机数。Gj是截止到第t轮搜寻的最优麦穗第j个物理指标值。xij(t)越大，对该项指标的搜寻速度越慢，反之越快。

2.3 筛选阶段

2.3.1 淘汰赛阶段

筛选阶段模拟竞赛过程，在小规模范围内搜索可能的最优解，包括淘汰赛和锦标赛两种筛选形式。淘汰赛是在挑战麦穗和标准麦穗之间进行，胜者作为下一轮的标准麦穗，所有获胜者形成新一轮标准群体。根据定义3和定义4，第t+1轮标准群体X(t+1)按式（20）、式（21）计算。

式（20）中，σ(x)是选择函数，x≥0 表示标准麦穗优于挑战麦穗或二者之间不具有优劣关系，选择标准麦穗xi作为优等麦穗进入第t+1轮标准群体。否则，选择挑战麦穗yi作为优等麦穗进入第t+1轮标准群体。

2.3.2 锦标赛阶段

锦标赛是在标准群体中筛选出最优麦穗。通过计算标准麦穗的成熟度值，选择成熟度值最大的标准麦穗作为最优麦穗，即问题的最优解。根据定义6和定义7，考虑标准麦穗的优劣关系及目标偏好，设计TCA 成熟度函数F(xi)，见式（22）。

其中，N为标准群体麦穗数，m为筛选目标数，fk(xi)为第k 个筛选目标函数，fk(xi)=1/zk(xi)。ψ(k)为偏好目标函数，取值见式（23）。ϕ(x)为筛选目标统计函数，取值见式（24）。

pf是筛选目标序号，由决策者根据偏好设定，pf∈[1，m]。

由式（24）知，任意两个标准麦穗的筛选目标统计函数值之和为0，即∑(φ(x)+φ(-x))=0。因此，∑F(xi)=0。

2.4 算法描述

步骤1：输入。需求点应急物资需求种类与数量q，供应点应急物资储备种类、数量c、单位重量w和单价p，供应点车辆数量h、载重量g、平均时速v 和单位运输费用ρ，竞赛轮数T，偏好目标pf，搜寻方向D（初始值为1），初始标准群体X。

步骤2：按式（8）至式（13）计算f1(x)，按式（14）至式（16）计算f2(x)。

步骤3：按式（22）至式（24）计算标准麦穗的成熟度F，保存最优麦穗（最优调度方案）x*及f(x*)。

步骤4：若达到最大竞赛轮数，则终止计算，转步骤9，否则，转下一步。

步骤5：按式（18）、式（19）搜寻挑战麦穗，获得挑战群体Y。

步骤6：按式（8）至式（16）分别计算挑战群体Y中挑战麦穗的筛选目标值f1(x)和f2(x)。

步骤7：按式（20）、式（21）逐一筛选标准麦穗和相应的挑战麦穗，胜者作为优等麦穗加入标准群体，产生新一轮标准群体X。

步骤8：更新搜寻方向D，转步骤3。

步骤9：输出。全局最优调度方案x*及调度时间f1(x*)和调度成本f2(x*)。

3 实证分析

3.1 数据与参数设置

2021 年河南特大洪涝灾害共造成17 个省辖市、1417.85万人受灾，直接经济损失达1767.03亿元。以此为算例背景，选择11 个受灾地区为应急物资需求点，9 个仓储为应急物资供应点，以大米、面粉、饮用水等6种物资为主要的应急救援物资。根据受灾情况设置各地区各类应急物资需求量。参考河南省应急管理厅、统计局、电商等官网数据，整理得到供应点物资储备、价格等数据，存储于相关数据集。

为验证调度模型的有效性和提出算法的性能，同时采用TCA、DE、GWO、GSA、NSGA-II 和PSO 求解最优调度方案。为便于对比，各算法初始群体相同，群体个体数N=20，误差精度e=[5.0，0.5]，调度份额上界lambda=15，最大迭代次数T=5000。

3.2 应急物资优化调度算法比较

应急救援工作要求在最短时间内将应急物资运送到受灾点，采取最近供应点调度的方案见表1。

表1 最近供应点调度方案

由表1 可知，最近供应点调度的总成本为2560.5 万元，调度时间是完成所有需求点应急物资运送任务的时间，故总调度时间为74.4小时。

为求解最优调度方案，并检验提出算法的优化效果，分别采用无目标偏好的TCA算法与其他五个算法进行对比实验，为避免算法的随机性，所有算法均计算30 次，取其平均值作为全局最优目标值。各算法求解结果见表2。

表2 最优调度方案

由表2 可知，无论是调度成本还是调度时间，无目标偏好的TCA 算法求解结果都明显低于其他算法。TCA 的调度成本远低于最近供应点调度方案，调度时间将近缩短一倍。各算法全局最优调度曲线变化趋势见图1。

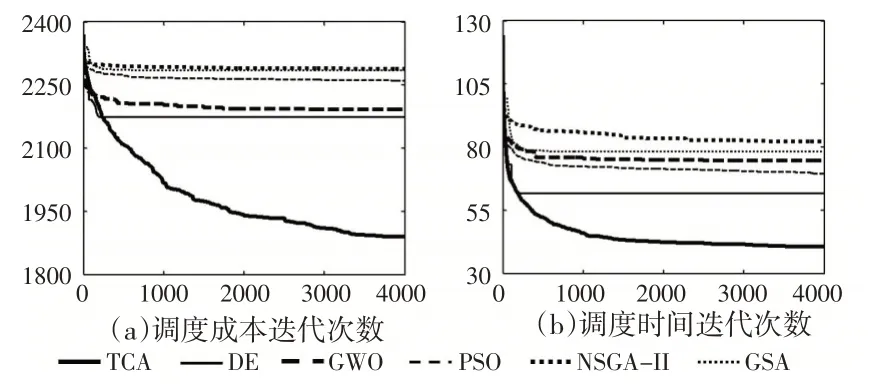
图1 全局最优调度目标曲线

图1（a）为算法最优调度成本曲线。1000次迭代计算内，DE 收敛速度最快，NSGA-II 收敛速度最慢。此后，除TCA外，其他算法基本趋于收敛，TCA却继续呈下降趋势，且远离曲线相对集中的其他算法。图1（b）为最优调度时间曲线。TCA曲线持续保持下降趋势，其他曲线均出现早熟收敛。可见，TCA优化能力明显优于相比较的算法。

3.3 考虑目标偏好的TCA优化调度

调度者根据目标要求设定目标偏好，为验证具有目标偏好的调度模型有效性和TCA求解多目标问题的优化能力，分别考虑调度成本偏好和调度时间偏好求解最优调度目标值，并与无偏好情形进行对比。优化结果见表3，算法均计算30次，取其平均值作为最优调度目标值。

表3 考虑目标偏好的TCA最优调度方案

由表1至表3知，考虑成本偏好的TCA求解的调度成本最低，与最近供应点调度相比，节约调度成本26.2%，此时，调度时间约为最近供应点调度的一半。考虑时间偏好的TCA求解的调度时间最短，仅为36.4小时，与最近供应点调度相比，节约调度时间51.1%，此时，调度成本也明显低于最近供应点调度以及其他算法求解结果。无偏好TCA两个目标值介于成本偏好和时间偏好之间，是一个折中方案。由此可见，TCA求解的应急物资优化调度方案均优于其他算法求解的优化调度方案。考虑目标偏好的TCA最优目标变化趋势见图2。

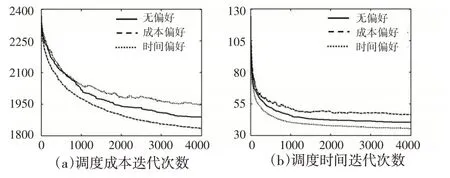
图2 目标偏好的TCA全局最优调度目标曲线

由图2 可知，无论是考虑成本偏好还是考虑时间偏好，相应的目标曲线都呈下降趋势，且三种情形下降趋势基本一致。表明考虑目标偏好的TCA 与无偏好TCA 一样，其最优目标是收敛的。

3.4 算法搜索性能比较

尽管包括TCA 在内的上述算法求解的最优目标均是收敛的，但算法的搜索性能不尽相同。每一代群体最优目标值变化趋势反映算法的搜索性能，所有算法的每一代群体最优调度时间和最优调度成本曲线见图3，其中TCA为考虑目标偏好情形。

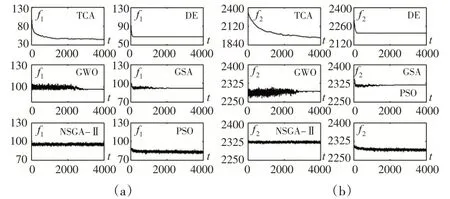
图3 每一轮群体最优调度目标曲线

图3（a）和图3（b）分别是调度时间和调度成本优化曲线，考虑目标偏好的TCA两个目标曲线基本不存在振荡，每一代群体两个最优目标值持续降低，直至收敛。其他算法两个目标曲线存在较大幅度振荡。由此可见，考虑目标偏好的TCA优化算法搜索性能明显优于相比较的算法。

4 结束语

实证表明，本文建立的应急物资调度模型能有效地降低调度成本，大幅缩短调度时间，可为应急物资优化调度提供决策参考。所提出的TCA 优化算法简洁高效，适合求解多目标优化问题，其优化精度和搜索性能均优于相比较的算法，可满足应急物资管理者的多目标调度决策需求。调度方案实值映射编码能够保持所有算法个体更新的有效性。当需求点和供应点数量较大、需求物资以及考虑目标较多时，调度方案解空间将显著增加，TCA 等优化算法计算效率降低，因此，对于具有更多调度目标和高维度决策变量的应急物资调度模型，提高TCA 算法的计算效率值得进一步研究。