基于有监督机器学习的旅客购票行为建模分析

张镫月，彭超华

（1.上海对外经贸大学国际经贸学院，上海 201600；2.南通大学机械工程学院，江苏南通 226019）

随着社会经济的发展，中国高速铁路的运营里程也经历了爆发式增长。高速铁路大大减少了人们的出行时间，提升了出行品质，同时以安全、换乘方便、乘坐舒适著称。但是选择高铁还是传统的火车出行，对不同的人来说，有不同的意愿。

为了更合理地研究旅客出行购票行为的规律，为铁路部门提供一些建议和意见，本文首先确立了旅客出行影响因素模型的基本架构，建立旅客购票行为与影响因素关系的数学模型。

随后基于Scott-Knott 检验对旅客购票行为的机器学习模型实证研究进行考核，从11 种有监督机器学习算法中选择泛化能力最好的机器学习模型，以此为基础建立旅客购票行为的计算模型，针对学生购票行为进行预测。

针对一定区域、特定阶段、具有代表性人群的购票行为进行探索性研究，分析高铁客运量与传统火车客运量的规律。

1 旅客购票行为与影响因素关系建模

1.1 数据预处理

本文所用的数据来自于2019年江苏省研究生数学建模科研创新实践大赛。共有161 人参与了信息统计，统计的特征如表1 所示。

表1 统计特征名称及简称

由于其中的一些指标无法表现出可区分的特征，因此本文需要剔除统计特征中的学号信息及起点终点信息。

旅客效用函数模型的求解依赖于经济性、快捷性、方便性、舒适性及安全性，而量化这些指标的基本特征可以概括为里程、行驶时长、个人收入及票价。本文对上述基本特征进行了可视化分析。

从分析结果来看，行驶里程在500～2 000 km 的人数占据了绝大部分，这符合火车/高铁长途出行的基本属性；其次统计到的行驶时长普遍在0～15 h，考虑到火车/高铁的行驶速度，这也与行驶里程相呼应；再次本文所研究的人群是学生群体，他们普遍的个人支配收入为2 000 元左右，这也决定了他们主要选择的购票价格为0～800 元。

考虑到旅客的个人可支配收入会对后续多个特征产生影响，本文对参与调查的学生群体的个人收入情况进行了三分位数分箱处理，以此将学生群体划分为高收入、中等收入及低收入群体，并进行0、1、2 编码，统计结果如表2 所示。

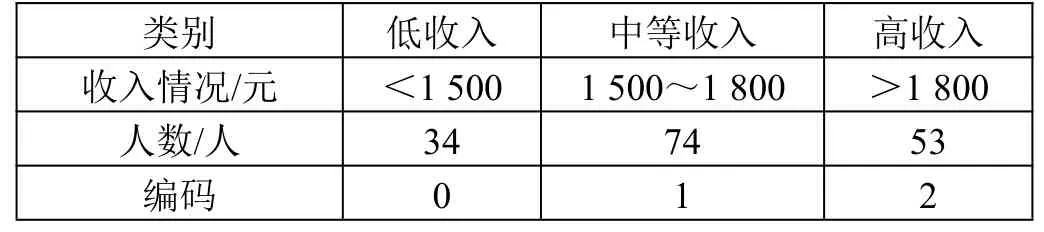
表2 学生群体收入划分

1.2 各特征影响及相互影响建模分析

结合上文初筛后的特征，本文给出了各特征相互耦合影响的示意图，如图1 所示。

图1 各特征相互耦合影响图

从指标筛选过程中可知，效用函数的求解还依赖于各交通工具的费率及旅客的时间价值。此处使用旅客的旅途时间价值替代时间价值，因此各交通工具的费率及旅途时间价值数学定义如下：

式中：Ri为第i种交通方式的平均费率的数值；Fi为票价的数值；Li为第i种交通方式的运行里程的数值；V（Ti）为旅途时间价值的数值；Ti为出行时间的数值。

引入这2 个特征后，对标签和特征进行Pearson相关性检验，结果如表3 所示。

表3 各特征与标签的Pearson 相关性检验

在引入费率和时间价值这2 个标签后，其与标签的Pearson 相关性检验结果超过了0.65，表现出了强相关性，因此，将2 个标签考虑在内使结果更加理想。

1.3 基于Fisher-Score 准则对特征影响程度建模分析

Fisher-Score 准则是由DUDA 等在2012 年提出的一种有监督的特征选择算法[1]。它根据是否隶属于同一个标签的特征的特征值进行筛选。该准则对于每个特征的评估得分描述如下：

式中：nj、μij、μi及uij2分别为类中的样本数、特征fi的平均值、类j中样本的特征fi的平均值及类j中样本的特征fi的方差值。

此外，Fisher-Score 准则可以视为拉普拉斯分数的一个特例，与拉普拉斯分数类似，它也可以通过贪婪选择原则类似获得具有最大Fisher 分数的特征来获得前个特征。基于上述评分模型，本文对上节通过了Pearson 相关性检验的10 个特征进行模型求解，结果如表4 所示。

表4 各特征Fisher-Score 得分

从各特征的得分及排序结果来看，时间价值和费率这2 个特征的影响程度均超过了0.7，在10 个特征中是最高的。

其次是行驶时长和票价这2 个特征的得分超过了0.2，但相比于时间价值和费率，这2 个指标的重要性明显降低。

其余的6 个特征的得分均未超过0.1，该结果表明这6 个特征的重要程度不及前面4 个特征。

1.4 旅客购票行为的机器学习模型实证研究

1.4.1 分析流程及伪代码

寻找最优的有监督学习算法，并以该算法为基础，建立可以预测旅客购票行为的数学模型。

分析流程图和项目执行伪代码分别如图2 及图3所示。

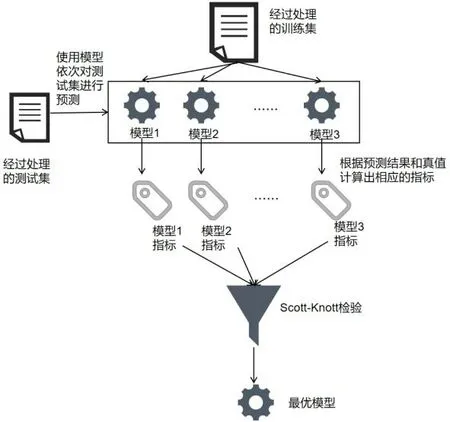
图2 分析流程图

1.4.2 模型准备

常用的11 种有监督机器分类器学习算法如表5所示。

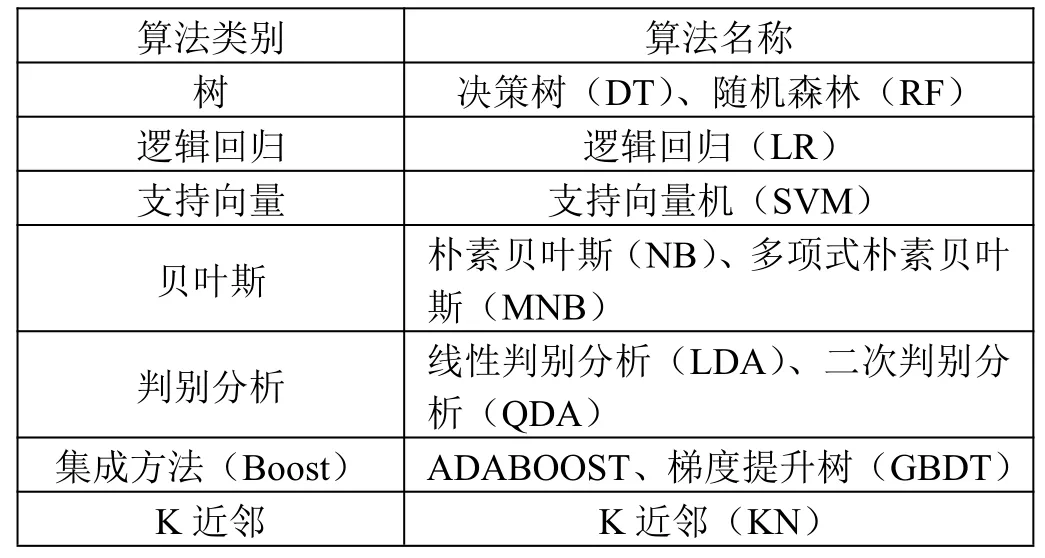
表5 有监督学习算法分类

1.4.3 显著性检验

使用Scott-Knott 检验[2]为本文考虑的所有方法（总共11 种）进行排序和分组。Scott-Knott 检验尝试将这些不同的方法划分到具有显著性差异的秩中（α=0.05）。具体来说，Scott-Knott 检验使用分层聚类分析为每个方法设置不同的秩。首先将所有方法基于平均性能（基于AUC 或F1指标）划分成2 组。如果处在一组内的方法仍存在显著差异性，则其会迭代使用上述过程将该组内的方法继续分组，直至组内的方法之间不存在显著差异性为止。

1.4.4 结果分析

执行图2 所示的流程及图3 的伪代码，并对模型训练的结果进行Scott-Knott 检验，检验的结果如图4所示。从查准率P来看，梯度提升树（Gradient Boosting Decision Tree，GBDT）优于随机森林（Random Forest，RF）及后面其他的有监督学习算法；从查全率R来看，二次判别分析（ Quadratic Discriminant Analysis Algorithm，QDA）优于RF（随机森林）及后面的其他算法；从F1的检验结果来看，RF（随机森林）在11 种有监督学习算法中的效果最好；从AUC（Area Under Curve，ROC 曲线下与坐标轴围成的面积）的检验结果来看，同样是RF（随机森林）表现出了最优的泛化能力。综上所述，RF（随机森林）是这11 种有监督学习算法中泛化能力最好的算法，因此，本文将基于RF（随机森林）建立可供计算的具体旅客购票行为的数学模型。

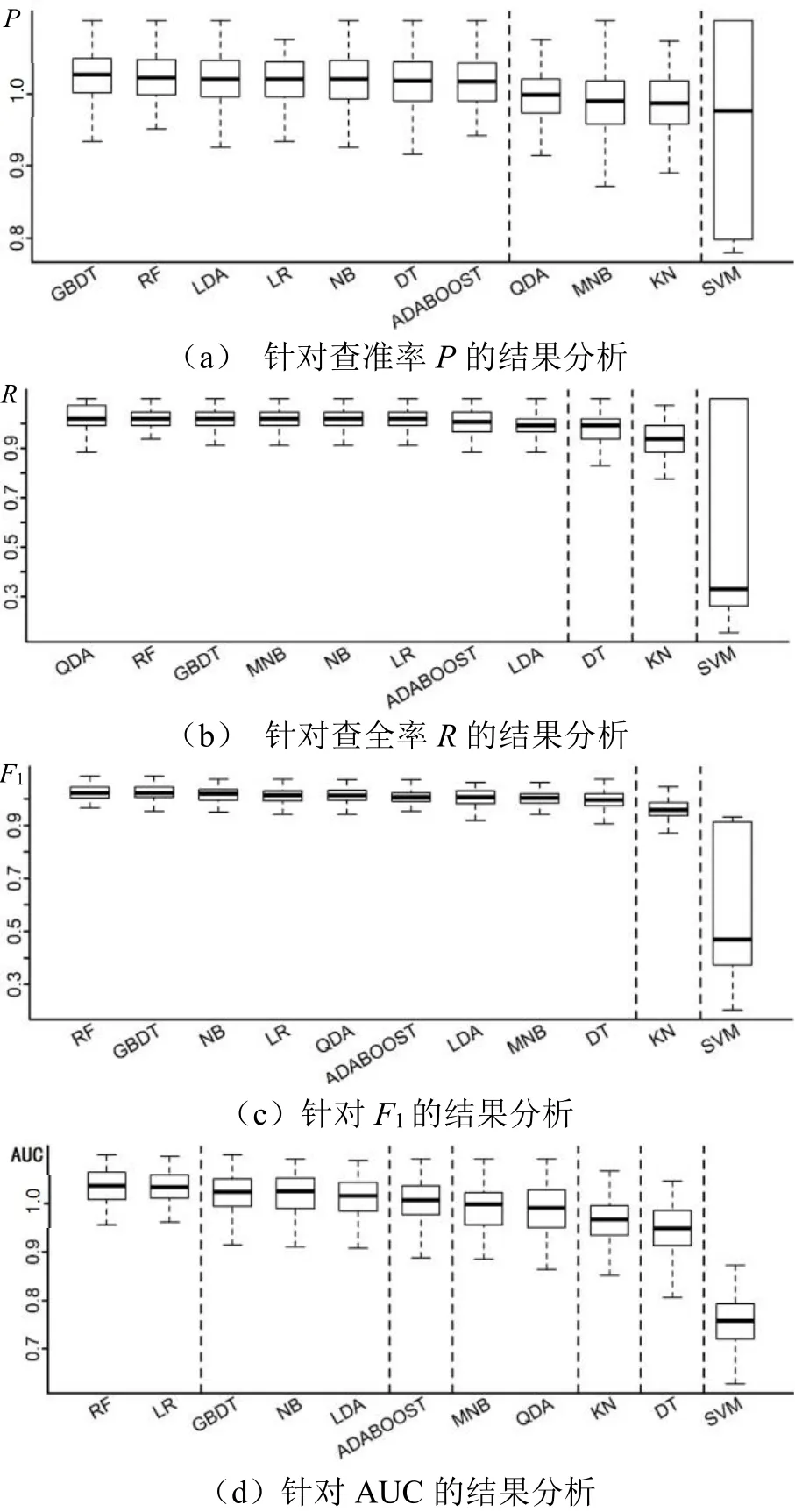
图4 检验结果

1.4.5 旅客购票行为计算模型建模

基于1.4.4 节对11 种机器学习模型的实证研究，选定了泛化能力最好的随机森林模型进行进一步的研究，它执行的主要流程如下。

1.4.5.1 产生训练集

随机森林采用的是有放回的无权重抽样。该方法先使用Bootstrap 抽样从原数据集中每次抽取n个训练样本，共进行k轮抽取，得到k个训练集，然后每次使用一个训练集来训练得到一个模型，最后将得到的k个模型采用投票的方式得到分类结果。Bagging 抽样方法是以可重复的独立随机抽样为基础的，在原数据集中的每个样本都有可能被抽到，但在重复多次后，有的样本是不能被抽取到的，不能抽到的概率是（1－1/N）N，N为原始数据集中样本的个数。

1.4.5.2 节点分裂与特征选取

随机森林采用的CART （ Classification and Regression Tree）决策树就是基于基尼系数进行特征选择，基尼系数的选择标准就是每个子节点达到最高的纯度，即落在子节点中的所有观察都属于同一个分类，此时基尼系数最小，纯度最高，不确定度最小。对于一般的决策树，假如总共有k类，样本属于第k类的概率为pk，则该概率分布的基尼（Gini）指数为：

由此可见，基尼指数越大，不确定性就越大；基尼系数越小，不确定性越小，数据分割越彻底。而CART 树是二叉树，上式又可以表示为：

在遍历每个特征的每个分割点时，当使用特征A=a，将D划分为2 个子集，即D1（满足A=a的样本集合）、D2（不满足A=a的样本集合）。则在特征A=a的条件下D的基尼指数为：

随机森林中的每棵CART 决策树都是通过不断遍历这棵树的特征子集的所有可能的分割点，寻找Gini系数最小的特征的分割点，将数据集分成2 个子集，直至满足停止条件为止。

1.4.5.3 森林形成与算法执行

重复上面单棵决策树样本抽样和构建每棵决策树2 个步骤，就建立了大量没有剪枝的决策树，这些决策树的组合就构成了随机森林模型。随机森林模型的最终分类结果是根据模型中每棵决策树的分类结果通过投票的形式得出的，得票最多的分类结果就是算法的输出结果。

2 旅客购票行为建模

2.1 效用函数模型

当运输通道内出现供城际旅客可选的交通工具为i种时，每种交通工具对应的效用值大小可用效用函数式来对不同交通工具特定的效用进行标定，城际旅客总是喜好效用值较低的交通方式，其数学表达式为：

式中：λn为第n项影响因素的权重值；为第i种交通工具的第n项影响因素，即上文中的票价、运行时间、方便性、舒适度及安全性。

2.2 机器学习模型

为了研究旅客购票行为发生的潜在规律，从数据本身出发，通过建立合适的机器学习模型训练分类器，然后对数据集进行交叉验证，并通过包括查准率P、查全率R、查准率和查全率的调和平均1/F1及ROC 曲线下的面积AUC 的值对机器学习模型泛化性能力进行评估。各指标的数学定义如下：

式中：TP和FP分别为混淆矩阵的真正例和假反例的数值；xi和yi分别为ROC 曲线的坐标点的数值。

将上文中的票价、运行时间、方便性、舒适度及安全性这些参数视为特征，将旅客的购票行为视为标签，建立有监督的机器学习的模型，其示意图如图5所示。

图5 旅客购票行为机器学习模型

3 旅客购票行为预测分析

通过1.4 节的建模分析与求解，建立了基于随机森林的有监督机器学习模型。为了提高模型的准确性和泛化能力，本文对所拥有的数据进行训练，进而得到训练好的学习器。用该学习器预测下一年寒假每个学生的购票行为，预测结果如表6 所示。

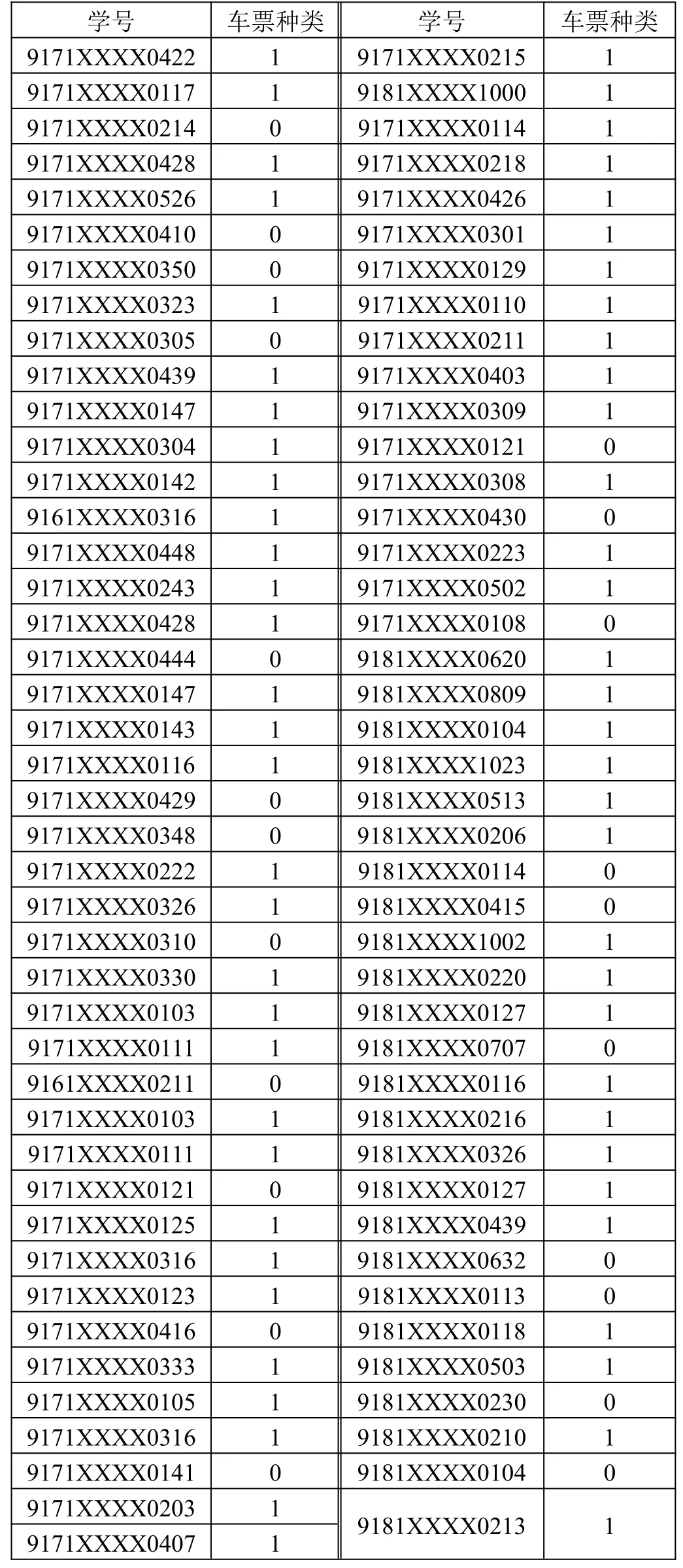
表6 下一年寒假每个学生的购票行为结果预测

将表6 预测的结果进行可视化，如图6、图7 所示。由图6 与图7 可知，购买火车票的人数约为22 人，约占总人数的25.88%；购买高铁票的人数约为63 人，约占总人数的74.12%。从预测的结果可知，虽然旅客购票行为受多方面因素制约，但是大部分学生在回程过程中还是更愿意选择高铁出行。

图6 购买不同种类车票的人数分布

图7 购买不同种类车票的人数占比分布

4 结束语

本文选定的区域为南京—上海、特定阶段为寒暑假期间、研究的代表性人群为大学生群体。其中南京—上海的轨道交通有京沪普铁、沪宁城际及京沪高铁。以黎晖关于《铁路出行方式选择行为模型研究》[3]的结论为基础进行讨论。总体上看，各铁路中性别分布比较均匀，在年龄分布上主要是18～45 岁的青年。各铁路乘客的学历分布呈现较大差异，京沪高速与沪宁城际乘客的学历较高，大部分乘客为本科及以上学历，而京沪普铁乘客以本科以下学历居多。在职业分布上，沪宁城际和京沪高铁主要服务对象为职员和学生，而这2 类群体在普铁占比较少。乘客收入分布特征为京沪高铁高于沪宁城际高于京沪普铁。而从出行目的来看，沪宁城际和京沪高铁中均有30%以上的客流为出差客流，京沪普铁则相对较少。

同时，笔者基于MNL（Multinomial Logit Model，离散选择模型）对乘客的出行意愿和影响因素进行了分析。结果表明，年龄对京沪普铁产生显著的正效应，乘客年龄越大，选择京沪普铁的概率越大。随着学历的增加，旅客选择普通铁路的概率降低。职业对京沪普铁具有突出的显著作用，尤其是对学生出行和职员出行的吸引力较低，这也侧面反映了节约时间、正点率高是学生与职员2 类群体的主要诉求。

上述研究结论表明了沪宁干线每天都有存在必要的需求，可称这些需求为基础需求Q。本文选定的人群为大学生群体，大学生经济是典型的“候鸟型”经济，由大学生寒暑假所造成的车站客流量拥堵也是具有“候鸟型”特征的，将这种“候鸟型”客流量称为Q′。Q和Q′的叠加势必会给铁路交通带来较大的负担。但是从研究结果来看，Q′是可以通过相应的计算方法和数学方法进行估算的。

因此，只有大致把握Q′的规模，才能使铁路局管理人员提前做好车辆车次等计划的安排。为了从更一般的角度描述对Q′的估计，给出以下解决方案：①铁路管理部门通过校园实地问卷调查或者面向大学生网上问卷调查获取相关信息；②铁路管理局通过后台比对筛选相应的调查对象；③结合后台数据与问卷调查数据形成有效的数据集；④对数据集进行特征工程处理；⑤进行机器学习训练，并预测结果。