Petri 网在STM32 主函数程序编写方法中的应用

孙 霞，缪玉婷，赵厚群，张坤乾，张 洁

（安徽理工大学 电气与信息工程学院 ，安徽 淮南 232001）

主函数是STM32 单片机执行程序代码真正实现功能的地方.复杂主函数程序编写过程中，需要分段编写并对其进行编译，查看是否存在错误.[1]Petri 网可以通过图形建模方式描述和分析复杂的工作流程[2]，提高程序编写的效率和准确性.本文通过Petri 网建模，对STM32 在Keil5-MDK 环境下主函数逻辑性编程，实现程序编写与运行的准确性与快速性，降低程序编写出错概率，提高效率.

1 基本概念

定义1[3]（流程模型）四元组N=(S,T;F,C) 满足以下条件，则称为有向网：

(1)S∪T≠Ø；(2)S∩T=Ø；(3)；(4) dom(F) ∪cod(F) =S∪T. 其中，dom(F)={x|∃y:(x,y)∈F};cod(F)={y|∃x:(x,y)∈F}.S元素代表库所，在Petri 网中一般用圆圈来表示；T元素代表变迁，在Petri 网中一般用方框表示；两种元素中至少一个元素为非空集合.F为流关系，一般用箭头表示，其只能连接不同类元素.

定义2[4]（变迁发生规则）令∑=(S,T;F,M) 为网系统，M是N=(S,T;F) 上的标识，t∈T，则具有以下的变迁发生规则：（1）t在M有发生权的条件是∀s∈S:s∈.t→M(s) ≥1，t在M有发生权的事实记作M[t＞.（2）若t在M有发生权，则在标识M下，变迁t可以发生，从标识M发生变迁t得到一个新的标识M′（记为M[t＞M′），对∀s∈S,

定义3[5]（可达性）设∑=(S,T;F,M) 为一个网系统，如果存在t∈T, 使得M[t＞M′，则称M′为从M直接可达的，如果存在变迁序列t1，t2，…,tk和标识序列M1，M2，…,Mk使得M[t1＞M1[t2＞M2…Mk-1[tk＞Mk，则称Mk为从M可达的. 从M可达的一切标识的集合记为R(M).

定义4[6]（行为轮廓）设(N,M0)是一个网系统，初始标识为M0，对任给的变迁对(x,y)∈(T×T)满足下列关系：（1）若x＞y 且y ≯x，则称严格序关系，记作x →y；（2）若x ≯y 且y＞x，则称严格逆序关系，记作x →-1y；（3）若x ≯y 且y ≯x，则称排他关系，记作x+y；（4）若x＞y且y＞x，则称交叉序关系，记作x‖y.

上述几种关系构成了网系统的行为轮廓，记作BP={ →,→-1,+,‖}

2 程序语句基本结构的Petri 模型

（1）顺序结构.顺序结构的程序语句Petri 网模型如图1 所示，语句1，2，3 执行顺序对应图中的T0，T1，T2，库所表示是否满足程序语句的执行条件，满足则执行，P0 与T0 执行语句1，以此类推.

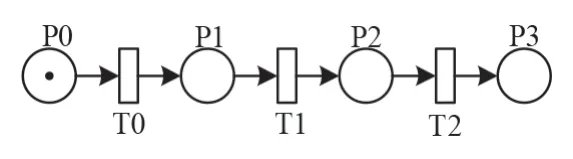
图1 顺序结构的程序语句Petri 网模型

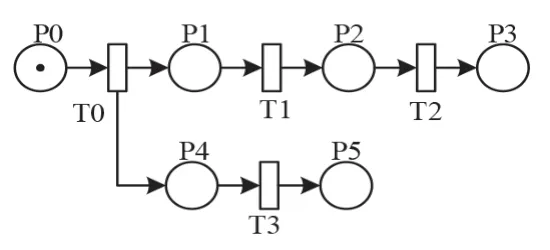
图2 分支结构的程序语句Petri 网模型

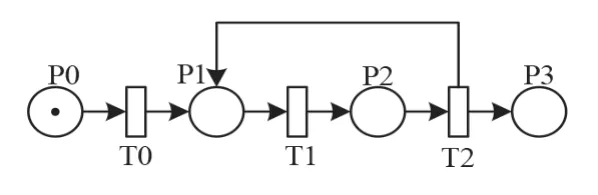
图3 循环结构的程序语句Petri 网模型

（2）分支结构. 分支结构的程序语句Petri 网模型如2 所示，语句1，3 执行顺序对应图中的T0，T1，T3. 其中，T0 为判断变迁，判断程序语句的执行分支. 若判断变迁T0 确定执行T1 表示的语句1，库所P1 满足执行条件后，开始执行程序语句1.

（3）循环结构. 循环结构的程序语句Petri 网模型如3 所示，语句2 执行顺序对应Petri 网模型图中的T2 到T1，T2 表示的程序语句2 执行完毕后，直接以库所P1 为执行条件，满足条件，开始执行T1，若不满足跳出循环结构.

3 主函数程序编写逻辑的Petri 模型

由于程序语句本身多样复杂，且编写时存在不同的结构与嵌套关系，致使程序员，尤其针对编程语言初学者，在编写STM32 主函数的程序时，不得不在编写一段程序后，就需要编译一次，再下载到单片机，查看是否能够实现预期功能.如果程序员将主函数中的所有程序全部编写完毕后再编译下载，除资深程序员外，出错机率高. 一旦出错，则需按照MDK5 编程工具报错之处，逐句改正，并且在改正时，往往会牵扯到程序的逻辑结构，出现“牵一发而动全身”现象.

本文利用Petri 网对STM32 的主函数程序编写逻辑进行建模. 此程序语句的Petri 网建模只针对STM32 单片机的主函数编程，以C 语言程序语句的逻辑结构为切入点，建立Petri 网模型，程序语句逻辑结构包括顺序结构、分支结构和循环结构. 主函数程序编写逻辑的Petri 网模型如图4 所示.

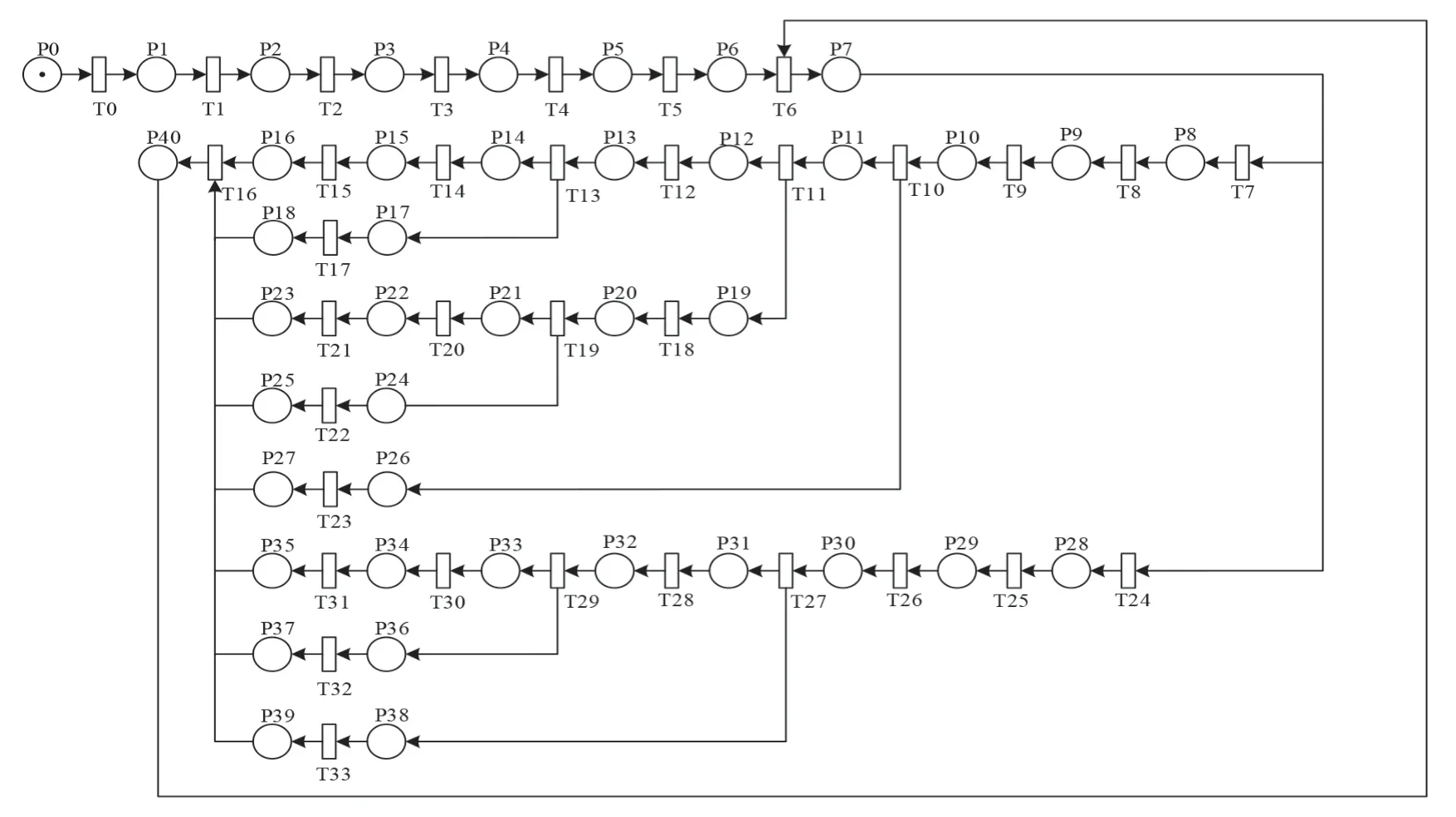
图4 主函数程序编写逻辑的Petri 网模型

图中库所P0 中的托肯代表程序员，T0 到T6 为顺序结构，程序员在编写主函数前，首先需要调用头文件包括传感器、定时器、蜂鸣器等设备具有功能定义性质的源文件，并依次对温湿度与光度的数值上限、蜂鸣器报警机制以及数据端口进行定义，编写主程序.首先，对端口与外设进行初始化，接下来开始执行程序；T6，T7 和T24 为分支结构，T6 为判断变迁，判断程序语句的执行分支，若判断变迁T6 确定执行T7 分支，则T7，T8，T9 发生，编写程序采集并读取温湿度信息且将数据通过串口输出在OLED 屏.T10，T11，T23；T11，T12，T18；T13，T14，T17 和T29，T20，T22 同样为分支结构，T16 到T6 为循环结构，T7 到T9 程序编写结束后，程序员再编写T10，判断温湿度是否超过上限值，若超过上限值，再判断是过温还是过湿，若过温，则编写T13，增加一次报警次数，当报警次数达到3 次时编程T15，T16，开始报警，报警结束之后延时一段时间继续循环执行程序，否则直接延时后继续循环执行程序，过湿程序的编写方法依此类推；若温湿度不超过上限值，则直接延时一段时间后继续开始循环机制；编写的T24 支路程序语句编写步骤与T7 支路相同.

4 主函数程序编写逻辑的Petri 网性能分析与验证

4.1 静态性质分析

主函数程序编写逻辑的Petri 网的性能可用关联矩阵A来分析其系统结构，关联矩阵的第i行j列的矩阵元素aij表示当变迁Ti发生时，库所Pi中消耗或产生n个托肯，其中n为负数时，表示消耗，反之表示产生.[7]

根据主函数的逻辑性编程的Petri 网的关联矩阵A，可得到公式AY=θ的通解Y，即A的S_不变量：

由结果知：从库所到变迁时消耗1 个托肯，从变迁到库所时产生1 个托肯.Petri 网中每一个S_都覆盖了一个库所，每个库所都会有托肯流过，S_不变量能够反映托肯的流动路径，具有不变性，因此此Petri 网的流程和托肯的流动路径是固定的.所以主函数逻辑性编程的Petri 网静态结构是稳定的.

4.2 动态性质分析

可达性是Petri 网最基本的动态性质.[8]主函数程序编写逻辑可达图如图5 所示，Mi代表可达状态标识集，可达标识集中“1”表示库所中有托肯，“0”表示无托肯，箭头方向表示状态转移.由图可知系统在运行过程中可以达到指定的状态，因此系统具有可达性.

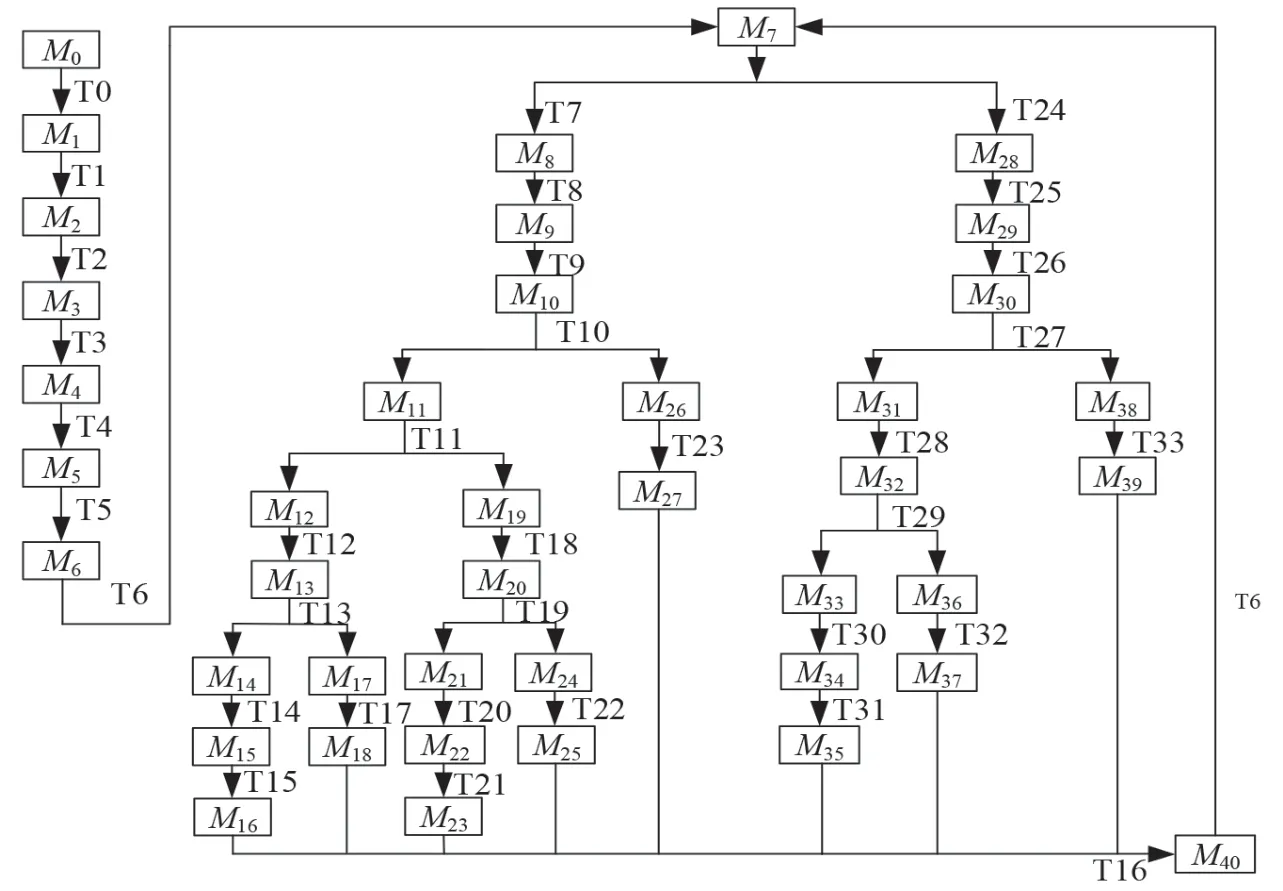
图5 主函数程序编写逻辑可达图

4.3 模型仿真检验

为检验Petri 网模型的正确性与可行性，用Petri 网分析软件PIPE 绘制模型图. 通过运行State Space Analysis 函数，对模型进行检验. 模型仿真检验图检验输出结果显示，系统的安全性、死锁性和有界性都是正确的，所以系统可以有效运行，此模型正确并且可行.

5 结 语

本文对主函数程序编写步骤进行Petri 网建模，分析主函数编写的流程，用PIPE 软件进行检验，证明其正确性与合理性. 本方法对简单的主函数的编写作用不明显，但对于外设多，须添加连接云平台，同时实现数据采集、设备控制、云平台信息指令上传下行的主函数，具有更好的效果.