基于景点空间异质性的景区旅游路线研究

李 雪，姚建盛，刘艳玲

（桂林理工大学 旅游与风景园林学院，广西 桂林 541006）

旅游路线设计是旅游活动顺利开展的重要组成部分.[1]为了获得满意的旅游路线方案，游客开始旅游活动前需要收集海量的信息，不仅耗费了大量的时间和精力，而且在面对各种相互冲突的目标时，游客难以做出最佳的旅游路线决策.[2]因此，研究旅游路线设计问题对于提高游客旅行满意度和提升景区服务质量尤为重要.

旅游路线设计研究内容主要集中在基于游客的审美疲劳[3]、酒店的选择[4]、交通方式[5]、旅游团中游客的异质偏好[6]、景区拥挤[7]等多个方面.Divsalar[8]将基于酒店路线设计问题分为整体酒店选择和局部景点选择，根据可变邻域算法对酒店和景点进行优化，得到更高得分的旅游路线方案. 郑伟民[9]以旅游团的总效用和单个游客的公平性为目标函数，将蚁群算法和差分算法相结合，为旅游团生成旅游路线. 旅游路线设计方法主要分为数据挖掘[10]和数学建模[1]两类. 李渊[12]对游客GPS 数据轨迹进行挖掘，为游客设计鼓浪屿半日和一日游旅游路线方案. 张九藤[13]基于景点得分和时间窗格进行建模，运用遗传算法，输出游客最高得分的旅游路线. 目前的研究多是将景点空间形态抽象为点状，即进入和离开景点都在同一个位置，对于只拥有一个出入口的景点来说是可行的，但没有考虑像长廊、桥等线状景点和像广场、博物馆等面状景点.[1]当游客游览完线状或面状景点时，可能会从不同于入口的出口离开，游客的空间位置发生了变化，直接影响到游客花费的路程时间和景点的游览顺序，从而影响到整个旅游体验.因此，有必要考虑景点不同的空间形态.基于此，本研究提出一种基于景点空间异质性的旅游路线设计方法. 通过构建景点空间异质性旅游路线数学模型，运用启发式算法，对虚拟景区进行实验，以期为游客设计出满足其个性化需求的旅游路线，丰富旅游路线设计研究内容和方法.

1 数学模型构建

表1 为本研究所需要的数学变量及其含义.V为景区中所有节点的集合, 由入口集(V1)、出口集(VF) 和景区中景点集(VA) 构成.为游客到达景区的时间,为离开景区的时间. 旅游活动应当发生在区的时间窗格范围内[to,tc],to为景区的开门时间,tc为景区的关门时间.Tmax为游客计划在景区中花费的时间预算. 景点的空间形态主要包括三类: 点状、线状和面状, 景点的空间形态会对旅游路线设计产生影响, 即游客对于不同出入口的选择将会生成不同的旅游路线.

表1 数学变量

1.1 目标函数

旅游路线设计的目标是在各种约束条件下，游客效用得分最大化. 游客效用得分与拜访的景点相关. 景点得分主要受景点吸引力和游客对景点偏好的影响. 游客拜访景点vi的得分可以通过式(1)计算.表示景点吸引力所占的权重，表示游客对景点偏好的权重，, 为了使游客从每个景点得到的效用值在0 到10 之间，函数乘以10.yi为决策变量，当游客访问景点vi, 则yi为1, 否则为0. 目标是最大化游客效用得分，用式(2) 表示.

1.2 约束条件

向游客提供个性化旅游路线服务时，需要满足各种约束条件，约束条件大致分为两种类型.

基础性约束 这些约束不受游客主观意愿影响，必须遵循才能确保设计的旅游路线具备有效性和真实性. 式(3) 保证游客开展的旅游活动在景区的时间窗格内，vm为游客选择的起点，vz为游客选择的终点.式(4)确保游客必须从景区入口集中的节点开始旅行，在景区出口集中的节点结束旅行，且起点和终点只能在景区的入口集和出口集被选择一次. 式(5) 表示旅游路线的连贯性且游客最多游览景点一次. 式(6) 确保旅游路线时间的连续性，从景点vi离开的时间加上vi到vj的路程时间等于到达景点vj的时间. 式(7) 确保游客从景点的其中一个入口进入景点，然后从其中一个出口离开景点，为如果游客从第k个入口进入景点vi, 则为1, 否则为为如果游客从第k个出口离开景点vi, 则为1, 否则为0.

个性化约束 游客想要旅游路线包含某些特征，并将其纳入到模型的解决方案中，满足个性化需求的约束函数. 式(8) 表示整个旅行时间不能超过游客的时间预算Tmax, 整个旅行时间包括游客在景点的游玩时间和旅游路线中景点间的路程时间.

2 模型求解

旅游路线规划问题是非确定多项式(NP-hard) 问题[3], 即在有限的时间内很难用精确方法求解. 考虑景区中景点的空间形态，游客个性化等因素，使研究问题更加复杂，求解难度更大. 启发式算法能在约束条件下，得到近似解，与精确方法相比求解速度更快. 蚂蚁搜寻食物的过程与游客游览景点的过程具有高度相似性，被广泛应用到求解旅游路线设计问题中[14], 因此，本文将改进的蚁群算法作为求解方法.

结合研究问题特点，对传统的蚁群算法进行改进.

初始化参数 参数主要包含三类：景点的信息和游客个性化需求( 起点集、终点集、景点集、节点游玩时间、节点得分、游客选择的起点、终点、节点间路径时间)，改进的蚁群算法中相关参数( 最大迭代次数iterMax、蚂蚁总数m、挥发系数r、信息素因子a、启发因子b、信息素增量Q);全局变量( 记录运行过程中相关数据).

蚂蚁生成路径 将蚂蚁放到游客选择的起点上，当游客没有选择起点时，从起点集中随机选择一个作为起点. 根据状态转移概率采用轮盘赌的策略选择下一个要访问的节点，将蚂蚁花费的时间加上到下一个景点的路程时间和游玩时间，判断是否超过游客的预算时间，如果超过预算时间，则判断蚂蚁路径上最后一个节点是否为终点，当为终点时，保存路径. 否则，蚂蚁重新旅行，直到满足要求；如果没有超出预算时间，局部更新，更新蚂蚁路径、蚂蚁花费的时间、禁忌表，根据景点的形态和禁忌表生成新的候选节点集.

全局更新 每次迭代后执行全局更新规则. 当m只蚂蚁都完成一次迭代，更新最佳路径、最佳路径效用和最佳路径花费的时间，为下次迭代做准备.

迭代次数是否满足最大迭代次数 满足最大迭代次数，结束操作；否则，迭代次数加一，转到蚂蚁生成路径阶段执行下一次迭代.

3 应用实验

3.1 实验信息

3.1.1 景区信息

景区中不同的景点空间形态类型不同，本研究选取22 个节点作为研究对象，为了更好地模拟现实中的旅游景区，设计了3 个线状景点，3 个面状景点和16 个点状景点.每个景点的空间形态和拥有出入口的数量(表2 第4 列)会影响旅游路线设计.节点之间不存在直接路径，将路程时间设为-1.游客可以根据自己的实际情况选择旅行的起点和终点，表2 中节点v1,v2,v3构成了景区的入口和出口集，将游客在起点和终点的停留时间设置为3 分钟.根据文献[3],从15 ～30 分钟随机产生19 个时间作为景点游玩时间；景点vi的吸引力Ai可以通过已经在景区游玩过的游客打分得到，旅游景点的吸引力呈长尾分布态势[15],研究使用python 中指数函数随机生成22 个数作为节点的吸引力值.

表2 景点属性参数

3.1.2 游客信息

通过向游客展示景点照片和使用文字描述得到游客对景点vi的偏好值Pi，在实验过程中拟定3 名具有不同旅游需求的游客对虚拟景区开始游览.根据景点的吸引力和游客对景区中不同景点偏好，随机生成22 个0 ～10 之间的游客偏好值.游客1 的时间预算为250 分钟，计划从节点v2进入景区，再从v2离开景区；游客2 时间预算为300 分钟，计划从节点v3进入景区，没有指定离开景区的节点；游客3 计划的旅游总时间为360 分钟，没有指定进入和离开景区的起点和终点，三名游客的旅游信息见表3.

表3 旅游者信息

3.2 实验参数

算法的参数严重影响算法的性能.蚂蚁数量设置的过大，会导致每条路径上的信息素趋于平均，正反馈作用减少，设置的过小，算法容易过早的收敛，陷入局部最优，全局搜索能力减低.通过灵敏度测试，将算法参数设置为a=1,b=2,r=0.4,Q=2,iterMax=100,m=200.根据式(9)对景点吸引力和游客对景点的偏好值进行标准化，消除量纲的影响.为了生成更加个性化的旅游路线，将设置为0.4,设置为0.6.

3.3 实验结果

3.3.1 更加个性化的旅游路线

旅游路线受游客个性化需求的影响. 游客在游玩之前通常有时间预算且会根据实际情况选择进入和离开景区的地点( 表3). 旅游路线如果没有考虑时间预算，游客会感到旅游行程匆忙，可能会出现没有时间游览其喜欢景点的情况，这将会影响到游客对这次旅行的评价.游客对景点的偏好会影响旅游路线中景点的选择.在设计旅游路线时，应当考虑游客的需求和偏好.

为了证明所提出的方法可以为游客设计个性化的旅游路线，根据表3 中给出的游客需求和偏好，为3位游客设置个性化的旅游路线(图1).游客1 的最佳旅游路线为v2,v9,v10,v8,v7,v6,v5,v2(图1 虚线),所花费的旅行时间为187 分钟，得到的效用为31.28.游客2 的最佳旅游路线为v3,v13,v8,v9,v11,v16,v15,v21v22,v1(图1 点划线),所花费的旅行时间为299 分钟，得到的效用为66.61.游客3 的最佳旅游路线为v2,v5,v6,v8,v9,v10,v11,v16,v18,v20,v19,v14,v12,v3(图2 点状线),所花费的旅游时间为355 分钟，得到的效用为48.93.可以看出，所提出的方法，可以根据不同游客的需求和偏好帮助游客设计个性化的旅游路线.

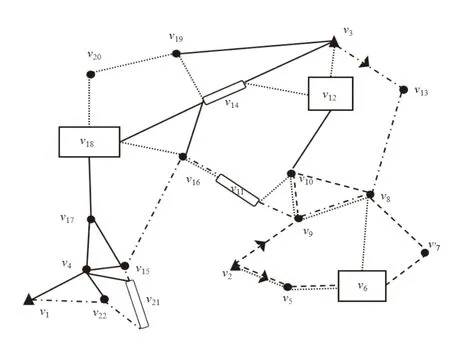
图1 不同游客的旅游路线(▲代表出口/入口，●点状景点，—线状景点，□面状景点)

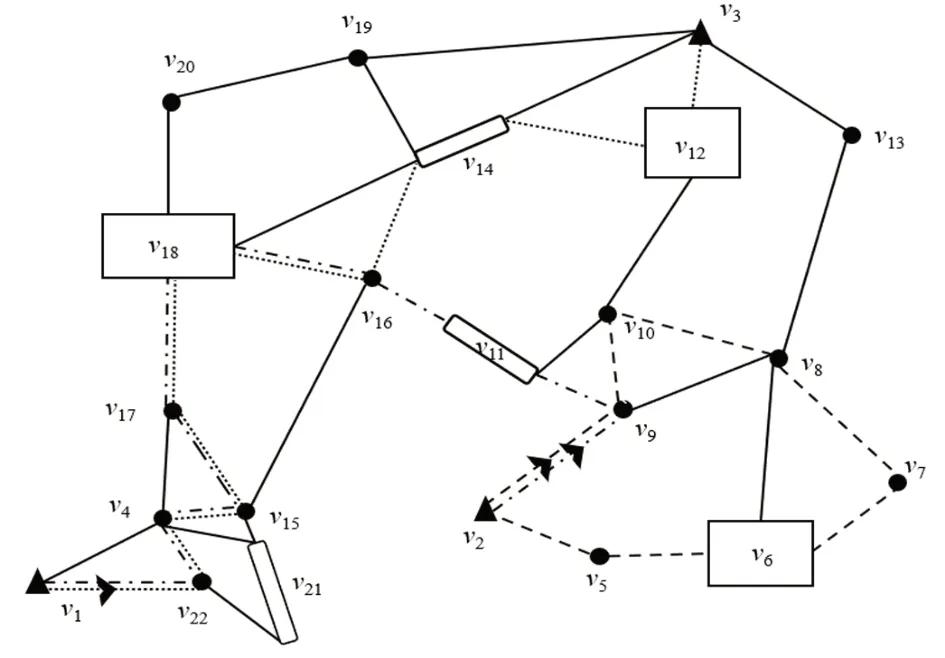
图2 不同情境下游客1 的旅游路线(▲代表出口/入口，●点状景点，线状景点，□面状景点)

假定在游客1 的时间预算和偏好不变的情况下，为游客1 设计两种情境，见图2.

情境1: 游客1 计划从节点2 开始旅行，不考虑离开景区的终点，得到的最佳旅游路线为v2,v9,v11,v16,v18,v17,v15,v4,v22,v1( 图2 点划线), 旅行花费的时间为236.5, 得到的效用为57.95.

情境2: 游客1 不再限定某个节点作为景区的起点和终点，从起点集和终点集中任意选择一个节点作为起点和终点，生成的最佳旅游路线为v1,v22,v4,v15,v17,v18,v16,v14,v12,v3( 图2 点状线), 旅行花费的时间为230 分钟，得到的效用为61.06.

当游客1 对旅游路线的要求变少时，旅游路线的多样性会增加，游客得到的效用会增多，这与实际生活相符合.

3.3.2 更加合理的旅游路线

目前研究只是将景点抽象为单一的点状，忽视了景点有多个入口和出口，导致出现不必要的折返( 重复走过的路线) 现象，使花费在路程上的时间增加. 游客花费在路程上的时间越长，则在景点的停留时间会缩短，从而使得游客所获得的效用减少.[5]基于景区中景点空间异质性旅游路线设计方法能够反映景区中景点的空间结构形态，帮助游客在旅行中避免不必要的弯路.

考虑景点形态与未考虑景点形态的方法对比. 当游客2 从节点v3出发，将v1作为终点时，未考虑景点形态的方法生成的旅游路线，游客在景点停留时间为221 分钟，花费在路程上的时间为76.5 分钟. 考虑景点形态的方法生成的旅游路线，游客在景点停留游玩时间为223 分钟，花费在路程上的时间为76 分钟. 考虑景点形态的方法花费在路程上的时间减少，在景点的停留时间增加，游客可以获得更大的效用.

本研究提出的方法考虑了景点的形态，可以避免出现折返的现象. 当游客1 计划将节点2作为旅行的起点和终点，预算时间为280 分钟时，未考虑景点形态的旅游方法生成的路线为v2,v9,v11,v10,v8,v7,v6,v5,v2( 图3 虚线), 游客1 花费的旅行时间为219.5 分钟，得到效用为26.319; 考虑景点形态的旅游方法生成的路线为v2,v9,v11,v16,v14,v12,v10,v8,v6,v5,v2( 图3 点划线), 游客1 花费的旅行时间为266.5 分钟, 得到效用为47.68; 考虑景点形态的方法和未考虑景点形态的方法设计的旅游路线都经过v9,v11,v10. 考虑景点形态的方法认为景点v11是线性景点，从进入v11, 后从离开v11, 游览了一次线性景点，没有出现折返现象. 而未考虑景点形态的方法从进入v11, 再游览完v11后，又从离开v11, 游览了两次线性景点，出现折返现象，路程时间增加.

图3 考虑与不考虑景点异质性的旅游路线(▲代表出口/入口，●点状景点，□线状景点，□面状景点)

此外，某些旅游景点存在多个入口和出口. 因此，在规划旅游路线时，选择合适的出入口对于提升游客的效用具有非常重要的意义. 本研究提出的方法考虑了景点的多个入口和出口，当游客1计划将节点3 作为旅行的起点和终点时，预算时间为300 分钟，未考虑景点形态的方法生成的旅游路线为v3,v12,v14,v18,v16,v11,v9,v8,v13,v3( 图4 虚线), 游客1 需要花费的旅行时间为293.5 分钟，得到的效用为56.95. 考虑景点形态的方法生成的旅游路线为v3,v12,v10,v9,v11,v16,v15,v17,v18,v14,v3( 图4 点划线), 游客1 需要花费 的旅行时间为285.5 分钟，得到的效用为60.81. 考虑景点空间形态的方法优化了景点出入口的选择. 未考虑景点空间形态的方法从进入景点v18，后从离开景点v18，进入景点和离开景点为同一个地点，在这个过程中出现了折返现象，游客的路程时间增加. 而考虑景点形态的方法，游客从进入景点v18, 后从离开景点v18, 这个过程中没有产生折返现象，花费在路程上的时间减少，游客获得了额外的效用.

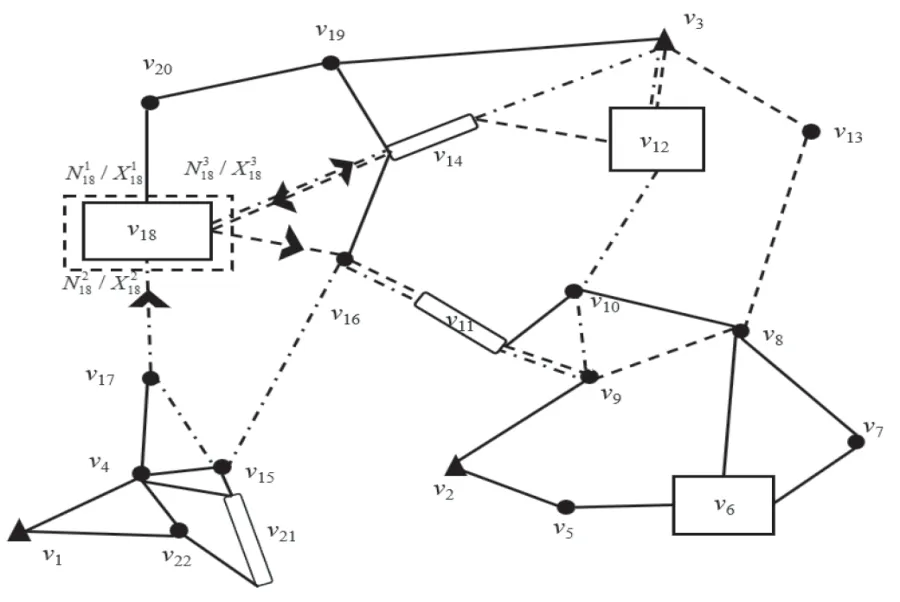
图4 考虑与不考虑景点异质性的旅游路线(▲代表出口/入口，●圆形景点，□线状景点，□面形景点)

4 结语

本文考虑景点的空间形态对旅游路线设计的影响,以景点的吸引力和游客偏好值组成的游客效用为目标函数,建立了基于景点空间异质性的旅游路线数学模型,并设计改进的蚁群算法求解.实验结果表明,构建的数学模型和求解算法能够生成优质的路线方案且具有普适性.研究还存在有局限性,构建的目标函数由景区的吸引力和游客偏好值组成,之后可以引入更科学更全面的方法对景点评估,通过数据挖掘等方法，更加客观的得到游客偏好.