一种结合驾驶员风险和车辆失稳风险的局部路径规划方法*
钱灏喆 孙文, 赵景波 郑剑锋 王军年
(1.常州大学,常州 213164;2.常州工学院,常州 213001;3.吉林大学,汽车底盘集成与仿生全国重点实验室,长春 130025)
主题词:Frenet 坐标系 驾驶员风险场 失稳风险 舒适性
1 前言
以高级驾驶辅助系统(Advanced Driver Assistance System,ADAS)为基础的智能网联汽车(Intelligent and Connected Vehicle,ICV)具备智能感知、决策规划和协调控制等功能,可有效减少因驾驶员失误造成的交通事故[1-2]。但随着智能驾驶的应用场景逐渐由单一场景过渡到复杂场景,由于智能感知重度依赖于传感器精度的提升,易导致决策规划出现失误,提高了事故发生的概率。
在环境感知方面,常见的方法可分为势场法[3]、时间逻辑法[4]、运动学法[5]和碰撞概率法[6]。势场法将障碍物所处位置视为势场源,根据感知到的环境势场引导车辆运动,但该方法以动作目的为导向,忽略了车辆执行器在运动过程中与行驶安全性有关的运动状态及其瞬时变化。时间逻辑法和运动学法从时间和运动学角度揭示了自车与障碍车纵向速度和距离的变化趋势,降低了纵向碰撞概率[7-10],但不适用于横向风险判断。碰撞概率法考虑了横向风险[11],但该方法对计算资源的高度需求限制了其在车端布置的可行性。以上方法均考虑了车辆本体的运动,也对交通环境风险进行了客观分析,但由于交通参与者具有随机性、时变性的特点,智能车缺乏驾驶员的主观理解,会出现风险判断失误的情况,因此上述方法在复杂度高、动态性强的交通场景下较难应用。
轨迹规划作为智能车决策规划的关键组成部分,可分为采样法[12]和搜索法[13]等传统方法和考虑车辆实际约束和性能目标的优化方法[14]。采样法可有效解决高维空间和复杂约束情形下的轨迹规划问题[15-16],但采样的随机性强,易陷入信息纠缠的局部最优问题。搜索法搜索能力强、灵活性好[17-19],但因过度追求搜索效率而忽视了道路的几何约束。为了有效结合高维度的环境感知风险,规划出一条满足动力学约束的无碰撞轨迹,优化法引入了评价指标,将多目标、多变量、多约束耦合的规划模型转化为有权重的目标函数并优化求解[20],更适用于以期望目标为参考、融合了交通要素多样性的复杂道路结构情况。
智能车通过模拟驾驶员认知实现正确的驾驶操作,一直是自动驾驶领域的研究难点。基于上述分析,本文提出一种结合驾驶员风险和车辆失稳风险的局部路径规划方法,进而确保自车在不同交通场景下的行驶安全性和舒适性。
2 坐标转换
在真实的交通环境中,根据驾驶员对交通场景的认知,其视域内不同位置都具有对应的风险强度,根据不同风险强度所构成的认知环境即为本文所采用的驾驶风险场,各点场强与所处位置相关。交通参与者在复杂交通环境下也具备某一碰撞风险,将交通参与者置于驾驶员视域内,其碰撞风险与风险场强的乘积即为该交通参与者在当前驾驶员认知内的风险势能[21]。
为了直观地表示车辆与道路之间的位置信息,降低车辆动力学的计算复杂度,以提高车辆不同时刻所处位置风险势能的准确度,需要对车辆所处位置进行笛卡尔(Cartesian)坐标系至Frenet坐标系的坐标转换。
如图1 所示,假设车辆t时刻在笛卡尔坐标系下位于点A(x,y),加速度为a,车速为v,航向角及曲率分别为θ和k,运动状态可表示为[x,y,v,θ,a,k]。遍历参考轨迹采样点寻找与当前位置A距离最短的采样点,记为A′。在笛卡尔坐标系下,A′点的运动状态可以表示为[xr,yr,vr,θr,ar,kr]。
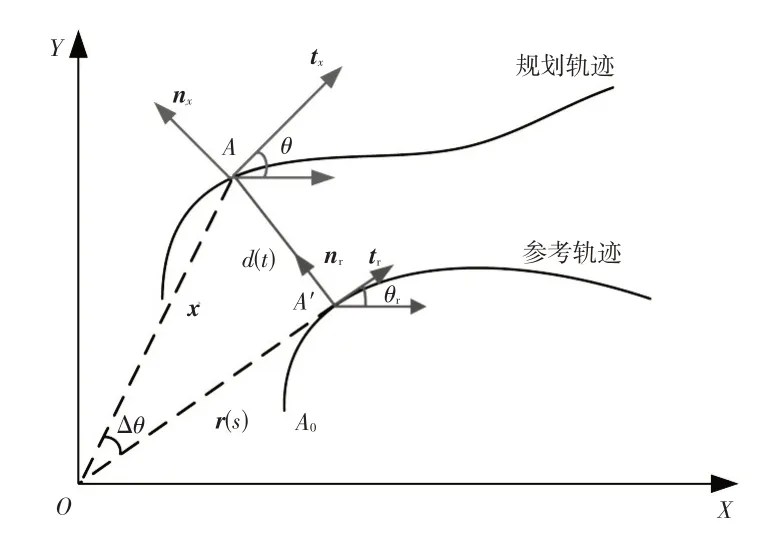
图1 笛卡尔坐标与Frenet坐标转换
以A′点为参考轨迹投影点,将笛卡尔坐标系下的运动状态投影至Frenet坐标系,x和r(s)分别为笛卡尔坐标系下车辆实际位置与投影参考点位置处的全局位置向量。
笛卡尔坐标系转换为Frenet坐标系的纵向、横向转换公式分别为:
式中,sr为笛卡尔坐标系下参考轨迹从起始位置A0到A′位置驶过的位移;Δθ=θ-θr为航向角之差;Δw=-为航向角的变化率之差;为笛卡尔坐标系下A′位置的曲率。
通过坐标转换将车辆运动状态以车辆与参考轨迹的横向位移d和纵向位移s表示,以(s,d)坐标直观表现车辆的具体位置及动力学特性,忽略了道路曲率的影响,降低了风险场构建和轨迹避障中参数计算的复杂度。
在Frenet坐标系下经规划得到横向、纵向运动轨迹后需要将其重新映射到全局笛卡尔坐标系以供控制模块调用。
3 基于改进驾驶员风险场的轨迹规划
为了充分评估驾驶员感知的交通风险,本文提出一种基于改进驾驶员风险场(Driver Risk Field,DRF)的轨迹规划算法,其技术路线如图2所示。本文以DRF为基础,引入交通参与者风险指标,将风险场内的道路边界、障碍车辆的风险因子视为定值,融合驾驶员风险和交通参与者风险,确定风险势能边界,完成对交通参与者的风险感知;同时,建立车辆稳定性风险场,以轮胎的附着椭圆力学公式为参考,探究车辆失稳的边界条件,并采用车辆失稳边界条件对轨迹期望的加速度进行约束,降低车辆失稳风险;轨迹规划部分,在Frenet 坐标系下通过多项式拟合生成候选轨迹集,利用三次样条曲线生成期望路径,基于风险势能边界和加速度约束对不满足约束的轨迹进行剔除,最后通过设计安全性代价函数和舒适性代价函数对候选轨迹进行择优。
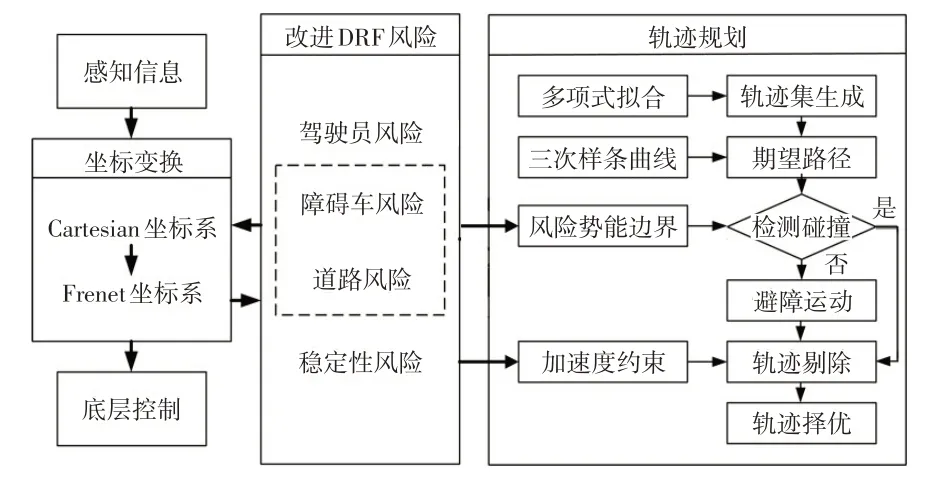
图2 基于改进DRF的轨迹规划算法技术路线
3.1 构建改进DRF风险模型
Kolekar 等[22]以势场法和运动学法为基础提出DRF模型,融合了车辆的实际状态参数,模拟驾驶员对交通环境风险的认知,以自车视角观测交通环境风险。本文基于DRF 模型,通过融合交通环境中的障碍车和道路边界对模型进行改进,实现自车对交通参与者的精确感知。结合将DRF模型与以车辆加速度为参考的稳定性风险场,构建综合的改进DRF风险场模型。
3.1.1 DRF风险场的基本原理
以自车为风险源,利用车辆运动状态和驾驶员特性参数建立三维高斯函数,对无人车感知到的风险进行表征,描述行车过程中车辆模拟驾驶员视角感知到的自车周围环境风险及其变化趋势。
在笛卡尔坐标系下,假设车辆所处位置为(x,y)、当前航向角为θ,根据轴距L与转向角δ的比值确定车辆行驶的固定圆弧半径Rcar:
车辆位置参数x、y、θ、Rcar共同确定了车辆转弯圆的中心(xc,yc),通过车辆转弯圆中心来预测车辆行驶路径的弧长,该圆弧长度l为驾驶员的前瞻时间tla与当前车速v的乘积:
根据转弯圆的弧长以及车辆的前轮转角δ构建高斯截面体,其高度A和宽度Wi分别为:
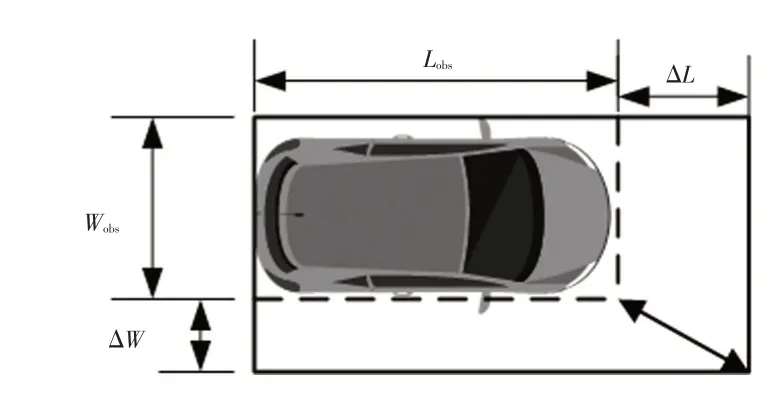
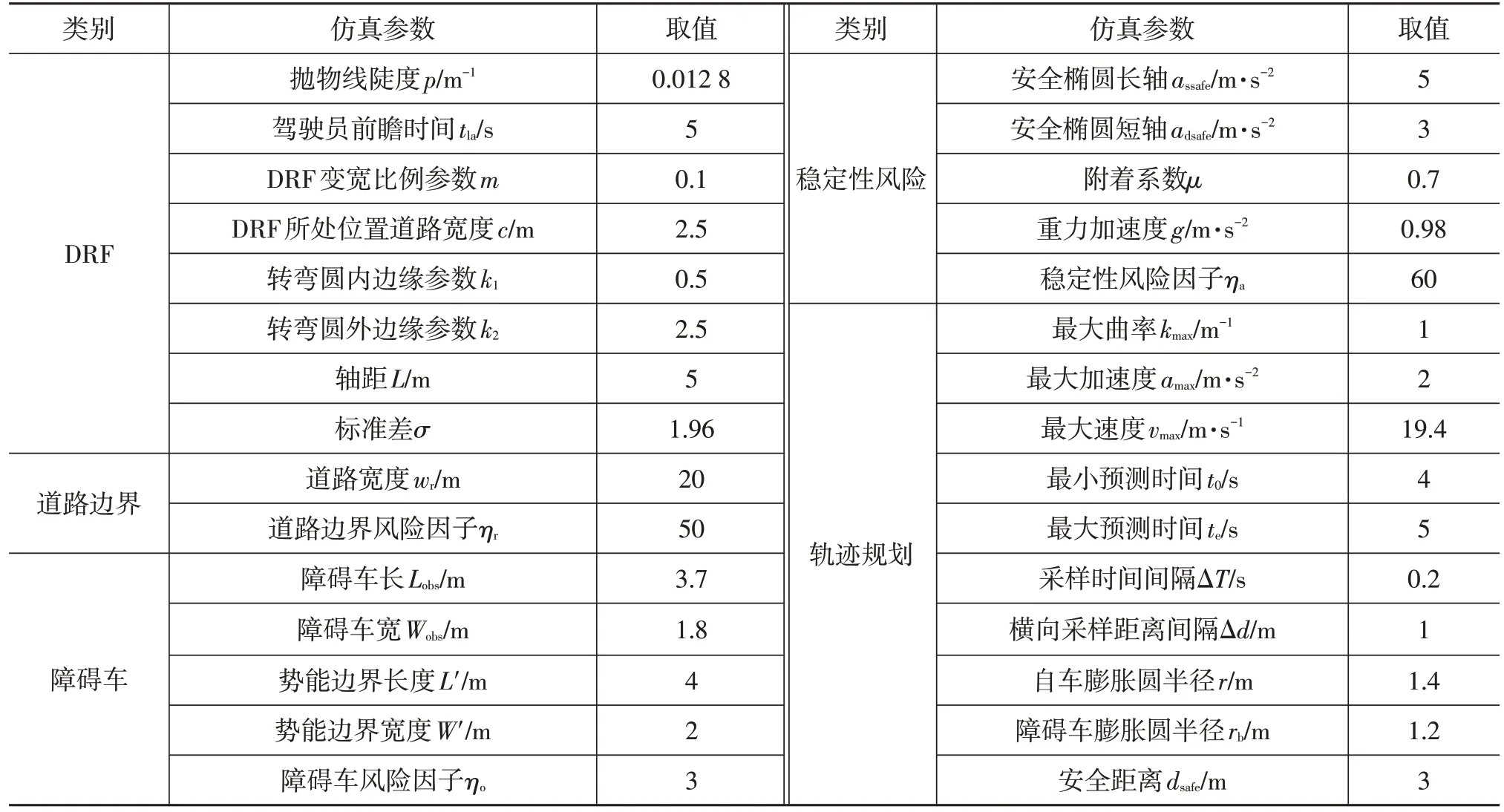
式中,p为抛物线的陡度,为定值;k1、k2分别为车辆转弯时圆弧的内、外边缘参数,由于车辆转角变化时,相同时间内外轮比内轮位移速度更快,因此分别定义k1、k2表征圆弧的内、外宽度;Wi分别对应圆弧内、外两侧边缘参数基于转角变化线性增加计算得到的DRF 模型的宽度,取k1 最终,将DRF 建模成包含以上所有参数的三维高斯函数Z(x,y): 式中,Z(x,y)为笛卡尔坐标系自车位置处的风险势能。 DRF 描述自车行驶过程中智能车模拟驾驶员视角感知到的环境风险。为了精确描述障碍物的位置,提高DRF 风险感知准确度,帮助自车进行障碍物检测和避碰,将DRF应用于Frenet坐标系,具体表达式为: 式中,Z(s,d)为Frenet 坐标系下自车位置处的风险势能;(sc,dc)为Frenet坐标系下车辆转弯圆的中心坐标。 3.1.2 改进DRF的建立 本文基于DRF原理,引入道路边界以及障碍车,提出一种改进的DRF模型。根据道路边界和障碍车对行车产生的安全威胁,赋予其不同的风险因子,融合风险因子与交通参与者的几何特性,产生不同交通参与者的固定风险成本并结合驾驶员风险和交通参与者风险成本,得到相应交通参与者在DRF内的风险。 3.1.2.1 障碍车风险 交通环境中的障碍车对自车行驶安全产生威胁,为了将DRF 与障碍车风险进行有效融合,将障碍车的形状定义为矩形,长和宽分别为Lobs和Wobs,其风险因子ηo视为定值,建立障碍车风险模型Ro: 3.1.2.2 道路边界风险 结构化道路边界保障了车辆在一定的范围内安全行驶,因此,道路边界处的风险远大于道路中心处的风险。设d<0 时表示车辆处于道路中心线左侧,d>0 时表示车辆处于道路中心线右侧,为了使车辆尽可能沿着中心线行驶,建立道路边界模型Rr: 式中,wr为道路宽度;ηr为道路边界风险因子,越靠近中心线取值越小。 3.1.2.3 稳定性风险 自车在避障过程中,由于地面附着系数不足,轮胎与地面摩擦力不足,过大的加速度易导致侧滑或侧翻等车辆失稳现象,失稳的力学表达式为: 式中,Ft为轮胎驱动力;as、ad分别为车辆的纵向和侧向加速度;μ为地面附着系数;M为整车质量;g为重力加速度。 为了描述加速度的安全区域,王安杰[10]建立了安全椭圆模型: 式中,Ra为稳定性风险指标;assafe、adsafe分别为安全椭圆的长半轴和短半轴;ae为椭圆内部点与原点连线交于椭圆边界上的点;ηa为稳定性风险场的风险因子。 障碍车风险和道路边界风险属于交通要素风险,其风险因子不随外界环境变化。为了将DRF模型与交通要素风险有机结合,使风险评估结果更加客观,本文提出交通参与者风险指标Rt,其为驾驶员风险Z和交通各要素风险指标(Ro和Rr)的乘积: 结合交通参与者风险和车辆失稳风险,提出总的改进DRF(Improved-DRF)风险: 式中,w1、w2分别为交通参与者的风险权重系数和车辆稳定性的风险权重系数;为保障主车安全稳定行驶,取w2>w1。 本文提出的改进DRF融合了交通参与者风险和车辆稳定性风险,通过融合车辆运动状态和自身的交通风险成本,对交通环境的风险进行感知。结合车辆稳定性风险,综合考虑车辆在行驶过程中遇到的风险,适用于自车模拟驾驶员在不同结构化道路下行驶的风险分析。 首先基于改进DRF 观测障碍物的形状和位置,在Frenet坐标系下生成候选轨迹和期望轨迹;然后检测自车与障碍车的距离以避免碰撞,在避障过程中考虑车辆失稳风险并对自车动力学进行约束,剔除不符合条件的轨迹;最后,设计安全性和舒适性代价函数对候选轨迹进行择优。 3.2.1 轨迹形式 采用横、纵向耦合的关于时间的五次和四次多项式生成轨迹:横向轨迹规划的主要目的是检测前方障碍物的位置,通过避障行为避免发生交通事故;纵向轨迹规划通过确定末状态来确定轨迹,避障过程中主要对速度和加速度进行规划。轨迹公式为: 车辆与道路边界距离越近,风险越大,因此利用三次样条曲线拟合车道中心线为期望轨迹g(x): 式中,c0、c1、c2、c3分别为三次样条函数的待定系数;x为三次样条曲线上插值点的横坐标。 设t0和te分别为整个规划时间段内最小和最大预测时间,根据单个规划采样周期ΔT进行离散采样,为使轨迹平稳结束,设定轨迹条件: 式中,(te)、(te)分别为末端横向速度和加速度;(te)为末端纵向加速度。 依据采样的横向位移Δd和车道宽度wr确定候选轨迹的数量。 3.2.2 碰撞检测 障碍物车辆及道路在DRF 内有很强的势能边界,边界内、外部风险存在显著差异。主车与障碍车需要保持一定的最小安全距离,本文通过以障碍车辆势能边界为起点构建横、纵向安全距离的安全扩展矩形区域来保证主车和障碍物车不受碰撞。图3 所示为安全扩展矩形势能边界区域。其中,Lobs、Wobs分别为障碍车的长度和宽度。在实际行车环境中,纵向风险大于横向风险,因此设定ΔL>ΔW。 图3 安全扩展矩形势能边界区域 安全扩展矩形势能边界的长度L′和宽度W′分别为: 以势能边界扩展区域为基础,采用滞后碰撞检测方法,如图4 所示,从障碍车安全扩展矩形区域后端依次向前端采用外接圆三等份分割方法判断主车与障碍物是否存在碰撞风险,自车采用二等份分割。计算各圆心间的距离,若距离小于最小安全距离dsafe,则检测为存在碰撞风险: 图4 碰撞检测示意 式中,(xobs,yobs)为障碍车质心坐标;(xi,yi)为轨迹采样点坐标;n为分割圆数量;rb为障碍车安全势能边界分割圆的半径: 同理,可求得自车分割圆半径r。 3.2.3 轨迹择优 车辆在行驶过程中,过大的加速度易导致车辆自身发生侧滑或侧翻。除此之外,车辆的运动特性具有极限,因此需要对主车动力学参数(曲率、加速度、速度)进行车辆状态检测,检测轨迹是否满足速度、加速度和曲率约束,并将不符合约束的轨迹剔除: 式中,kmax为允许的最大曲率;amax为允许的最大加速度;vmax为允许的最大车速;ki、ai、vi分别为候选轨迹按照采样周期ΔT离散化后对应的离散曲率、加速度和速度;i为候选轨迹离散轨迹点的序号。 碰撞检测作为一种考虑自车和障碍车几何特性的避碰方法,是避免自车和障碍车碰撞的强约束手段,可在多种静态或动态障碍物条件下保证自车行驶的安全性。碰撞检测代价函数fobs为: 式中,fobs_n(z)为第z条候选轨迹N个离散轨迹点与障碍物n的碰撞检测函数;dn为第z条候选轨迹上离散轨迹点与单个障碍物n的检测距离。 将不满足车辆状态约束的轨迹剔除后,从安全性和舒适性的角度设计总的代价函数,从保留的备选轨迹中选择一条最优轨迹。此时设计的安全性代价函数为自车行驶过程中感知到的交通环境风险,作为软约束条件选取改进DRF离散风险最低的安全路径作为当前规划的风险代价函数frisk: 为了使轨迹相对平滑,保证驾乘的舒适性,在数值上用纵向运动加加速度在时间域内的积分代表舒适性指标引入目标函数,记为驾驶冲击度Js: 但针对横向运动,主要实现避障功能,需要描述实际轨迹与参考轨迹的横向误差,设计偏移代价函数fd: 因此,横向运动的损失函数fd定义为: 式中,wd1、wd2、wd3分别为碰撞代价函数权重系数、风险代价函数权重系数、偏移代价函数权重系数。 针对纵向运动的速度规划,需要描述实际速度与参考速度vtarget的误差: 因此,纵向运动的损失函数定义为: 式中,ws1、ws2分别为驾驶冲击度权重系数、速度误差权重系数。 总的损失函数为: 式中,wd、ws分别为横向运动权重系数、纵向运动权重系数。 本文所提出的基于改进DRF的轨迹规划方法能够对道路边界和障碍车进行避障,在避障过程中对速度和加速度进行规划,以满足驾乘舒适性要求。此方法适用于不同结构化道路下自车的行驶安全性和舒适性需求。由于横向运动中以自车与障碍车不碰撞为首要目的,本文选取wd1=0.5、wd2=0.3、wd3=0.2;速度规划中选取ws1=0.5、ws2=0.5;在总的损失函数中安全性代价大于舒适性代价,因此选取wd=0.7、ws=0.3。 本文设定不同的工况进行仿真分析与硬件在环测试,验证基于改进DRF 的轨迹规划算法在直线和曲线道路场景下的车辆的行驶安全性和舒适性。在MATLAB平台搭建长度为140 m、宽度为20 m的双车道直线和S 车道场景,在场景中不同位置添加障碍车,验证改进DRF 模型的环境风险识别能力以及此规划算法在不同结构化道路中的避障能力;在避障过程中,选取轨迹的加速度曲线验证算法规划轨迹的舒适性。本文基于MATLAB 2020b仿真平台完成模型搭建,具体仿真参数如表1所示。为了提升仿真精度,所采用的主机处理器为Intel®CoreTMi7-10700 CPU,显卡为NVIDA Geforce GTX 1650。 表1 基本仿真参数 驾驶员风险场根据当前车速v和车轮转角δ的变化而动态变化,由于三维坐标系很难直观比较道路不同位置处的风险势能变化情况,因此将三维下的DRF 风险势能投影到二维s-d平面上,观测其在不同车速和不同转向角下的风险变化情况,自车当前处于二维s-d平面的(0,0)位置,其动态变化如图5所示。 图5 DRF动态场模型 由图5a可知,在车速为10 m/s 的情况下,DRF 的风险势能集中在0~35内,且随着与自车间距离增大,风险势能递减至0,纵向检测距离约30 m。由图5b 可知,在车速为30 m/s时DRF风险势能显著升高,风险势能集中在0~300内,纵向检测距离变长,约为80 m,此时纵向碰撞风险大于横向碰撞风险。由图5c 和图5d 可知,在不同前轮转角下DRF 模型会相应弯曲,转向侧DRF 观测的范围从10 m 逐渐变广且风险势能相应提升,此时横向碰撞风险大于纵向碰撞风险。因此,DRF动态场模型能准确反映自车运动状态变化条件下自车周围环境风险变化的趋势。 在DRF动态场的基础上,融合道路边界风险、障碍车风险对DRF 进行改进,如图6 所示。由图6 可知,对于道路边界风险,在直线行驶时,主车对于道路的风险感知均匀分布于两侧,而在一定转角条件下行驶时,横向碰撞风险加大,转向侧风险显著增高,另一侧风险显著降低,但均大于直线行驶时的风险。 图6 道路边界风险势能 障碍车风险势能如图7 所示。由图7a 和图7b 可知:障碍车与自车距离很近时,接近0 m 处的风险势能非常高,约为100;距离较远时,10 m处的风险势能相对较小,约为70,符合碰撞概率随距离变化的趋势。但是障碍车在DRF 内存在很强的风险区域,其大小与障碍车形状大小相同,风险区域明显区别于非风险区域,存在势能边界。由图7c和图7d可知:车速为30 m/s时,障碍车与自车距离很近时,接近0 m 处的风险势能非常高,约为1 000;距离较远时,10 m 处的风险势能相对较小,约为800,远大于图5b无障碍车时的风险势能,约为0~300。此时纵向碰撞风险极大,符合车速大时碰撞风险增大的客观规律。相比较图7a 和图7b,图7e 和图7f前轮转角δ=50°时,风险势能相对于直线行驶时没有增加,但是此时横向碰撞风险大于纵向碰撞风险,且障碍车存在明显的势能边界。当车速较快且存在一定转角时,由图7g 和图7h 可知,纵向和横向碰撞风险均极大,反映了车辆在车速过快且以一定转角行驶时的危险性。 图7 障碍车风险势能(θ=0°) 因此,综合对比图6和图7可知,道路边界及障碍车均存在很强的势能边界,边界内风险势能很大,边界外风险势能很小,此势能边界是区分风险区域和非风险区域的有效手段,在轨迹规划时需要对风险区域进行规避,保障行车的安全性。 车辆稳定性风险与车辆的加速度有关,在Frenet坐标系下需要对侧向加速度ad和纵向加速度as进行约束,利用assafe和adsafe设定安全椭圆区域,由于车辆行驶的过程中,纵向风险大于横向风险,所以assafe>adsafe。此外,轮胎附着系数μ是确定车辆失稳边界的条件。 车辆稳定性风险场如图8所示,安全椭圆内部的风险值为0,在安全椭圆外部与椭圆边界之间,风险值很大,接近60,符合自车由于轮胎与地面附着能力不足,纵向和侧向加速度过大,失稳边界处稳定性风险大的特点。 图8 车辆稳定性风险场 为了验证直线和曲线道路场景下基于改进风险场的轨迹规划算法的安全性和稳定性,本文分别设置直线和曲线道路下静态与动态障碍物的4 种工况展开仿真验证,矩形区域为DRF风险感知到的障碍车势能边界。 工况1:以直线车道中心线为期望路径,道路长度为140 m。主车起始车速为40 km/h,与自车纵向距离33 m处有静态障碍车1,纵向距离63 m处有静态障碍车2,纵向距离73 m处有静态障碍车3。 工况2:以直线车道中心线为期望路径,主车起始车速为40 km/h,在初始时刻,与自车纵向距离35 m 处有动态障碍车1,以20 km/h匀速运动,与自车纵向距离80 m处有动态障碍车2,以10 km/h匀速运动。 工况3:以S车道中心线为期望路径,主车起始车速为40 km/h,在曲率半径为50 m 的S 车道上行驶。与自车纵向距离33 m 处有静态障碍车1,纵向距离63 m 处有静态障碍车2,纵向距离73 m处有静态障碍车3。 工况4:以S车道中心线为期望路径,主车起始车速为40 km/h,在初始时刻,与自车纵向距离35 m 处有动态障碍车1,以20 km/h匀速运动,与自车纵向距离80 m处有动态障碍车2,以10 km/h匀速运动。 图9所示为4种工况下轨迹规划避障仿真结果。由图9a可知,由于障碍车1在期望轨迹的左侧且与自车距离大于安全距离3 m,因此自车无需规避。障碍车2、障碍车3 处于期望轨迹中心,自车在30 m 处感知到障碍物,并向右行驶进行规避,规避完成后继续沿期望轨迹行驶。由图9b可知,动态障碍车1在中心线左侧沿直线行驶,其与自车的距离始终大于安全距离,因此自车无需规避。障碍车2位于中心线上直线行驶,自车在与障碍车相距30 m 处识别到障碍车,向右行驶有效规避了障碍物,规避完成后40 m 处回到期望轨迹行驶。由图9c可知,障碍车分布在期望轨迹右侧,自车在30 m处识别到障碍车1,并向左行驶完成了有效规避。规避完成后由于障碍车2和障碍车3位于右侧,自车继续沿当前道路向前行驶,在规避障碍车3 后40 m 处回到期望轨迹。由图9d 可知,规划的轨迹有效规避了中心线的动态障碍物,规避完成后继续沿着期望轨迹行驶。 图9 轨迹规划避障效果仿真 图9b 和图9d 所示规划时间段内动态障碍车的运动变化情况。整个轨迹规划时间段5 s 内,动态障碍车1 共行驶了27.8 m,动态障碍车2 共行驶了13.9 m。截取时间周期1 s 动态位移变化,障碍车1 位移间隔为5.56 m,障碍车2位移间隔为2.78 m。 图10 为本文分别4 种工况下自车开始感知到障碍物、开始躲避障碍物、规避完成以及回到道路中心线4个典型阶段代价函数的仿真结果,分别对应直线静态避障车道纵向距离47 m,直线动态避障车道78 m,S 车道静态避障车道93 m以及S车道动态避障125 m处,说明改进DRF具备识别交通风险的能力。 图10 代价函数对比 由图10a~图10c可以看出,碰撞代价和风险代价可精确识别障碍物的位置,分别为候选路径z为14、10 和11 的位置,位于道路中心线的左侧和中心位置。从风险代价函数中可以看出,当DRF感知到障碍车时,障碍车风险远大于道路边界风险,此时引导自车选择更合理的避障方式。从图10d中可以看出,自车躲避障碍物并回到中心线后,碰撞代价和风险代价为0,说明位于中心线位置的自车目前安全。图10 中,偏移代价显示越靠近中心线,自车越安全,符合自车因道路风险沿中心线行驶的期望。最后,此规划基于总代价选择最优路径,引导自车选择对应的候选路径序号z,z分别为9、8、13和11,包含从开始识别障碍风险继而躲避障碍物,最后回到道路中心线的完整过程。 为了验证本文提出的基于改进DRF的轨迹规划方法的实效性,搭建基于dSPACE控制器的硬件在环测试平台,如图11所示,对轨迹规划的避障能力进行测试和验证。 图11 硬件在环测试平台 硬件在环测试的基本流程为:dSPACE 控制器实时运行轨迹规划算法,将车辆状态信息发送给CAN总线,CAN 总线将获取的车辆和车道线信息,以及求解得到的转向盘转角和车速指令信息反馈给上位机,并通过CarSim软件反映车辆动力学特性和模拟驾驶交通场景,实现虚拟场景下的硬件在环测试。 在轨迹规划过程中,设置仿真步长为0.2 s,在硬件在环测试中,搭建横、纵向PID 轨迹跟踪控制器对轨迹和侧向加速度进行跟踪,设置车速为40 km/h,控制步长为0.01 s,验证此规划算法在控制器中实时性。 硬件在环测试获得的轨迹如图12所示。由图12可知,实际轨迹与规划轨迹在整个行驶过程中误差很小。直线车道静态障碍物避障工况下,在纵向距离80 m处,自车规避障碍物后向左行驶时误差为0.04 m;直线车道动态障碍物避障工况下,在纵向距离78.6 m处,自车检测到障碍物向右避障时误差为0.01 m;S车道静态障碍物避障工况下,在纵向距离110 m处检测到障碍物向右避障时,误差为0.03 m;S 车道动态障碍物避障工况下,在纵向距离100.5 m处,检测到障碍物向右避障时误差为0.02 m。综合图12a~图12d可知,结合控制器的基于改进DRF的轨迹规划方法跟踪误差小,均在0.1 m以内,且轨迹平滑性好,满足控制器的实时性需求,保障了车辆的行驶安全性。 图12 轨迹规划硬件在环测试结果 图13 所示为4 种工况下自车避障的侧向加速度仿真和测试对比结果,由图13可知:直线车道静态避障侧向加速度峰值、直线车道动态避障侧向加速度峰值、S车道静态避障侧向加速度峰值、S车道动态避障侧向加速度峰值分别小于2 m/s2、0.95 m/s2、1 m/s2和1.2 m/s2,均低于约束值3 m/s2,满足驾乘舒适性需求;通过硬件在环测试得到的实际侧向加速度与规划侧向加速度误差较小,在0.1~0.5 m/s2范围内,进一步验证了结合PID 轨迹跟踪控制器的跟踪性能良好,说明此轨迹规划算法在降低碰撞风险的同时,保证了车辆的舒适性。 图13 侧向加速度变化对比 本文提出了一种交通风险与DRF 风险融合的方法,基于DRF 模型,融合交通参与者的风险成本,使驾驶员视域内的交通参与者风险随DRF动态场产生相应变化,增加了环境风险感知的准确度。同时提出了一种基于风险势能的轨迹规划方法,在Frenet坐标系下以驾驶员视角感知全局路径下的障碍物位置,基于改进的DRF 对风险高的点进行规避,保障行车的安全性,并且基于稳定性风险场对车辆加速度进行约束,保障行车的舒适性。仿真和硬件在环测试结果表明,规划的轨迹在满足避障的同时,具有良好的回归特性,能够沿着期望轨迹继续行驶,同时,其加速度在约束值范围内,保障了驾乘者的舒适性。 本文在融合交通参与者时,考虑了道路边界和障碍车2 种交通要素,后续可对交通参与者种类进行拓展。在考虑交通参与者成本时,依据驾驶员主观进行判断,存在不确定性,后续也将选取客观方法对交通参与者成本进行进一步分析。3.2 基于改进DRF的轨迹规划

4 仿真分析与测试验证
4.1 改进DRF风险
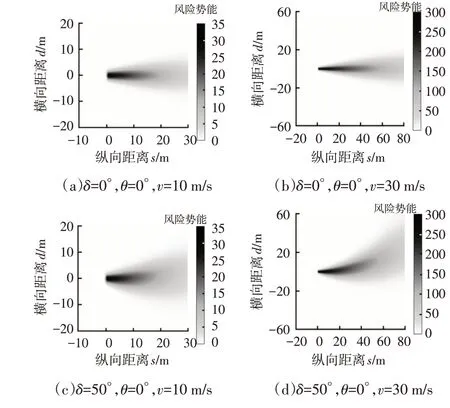

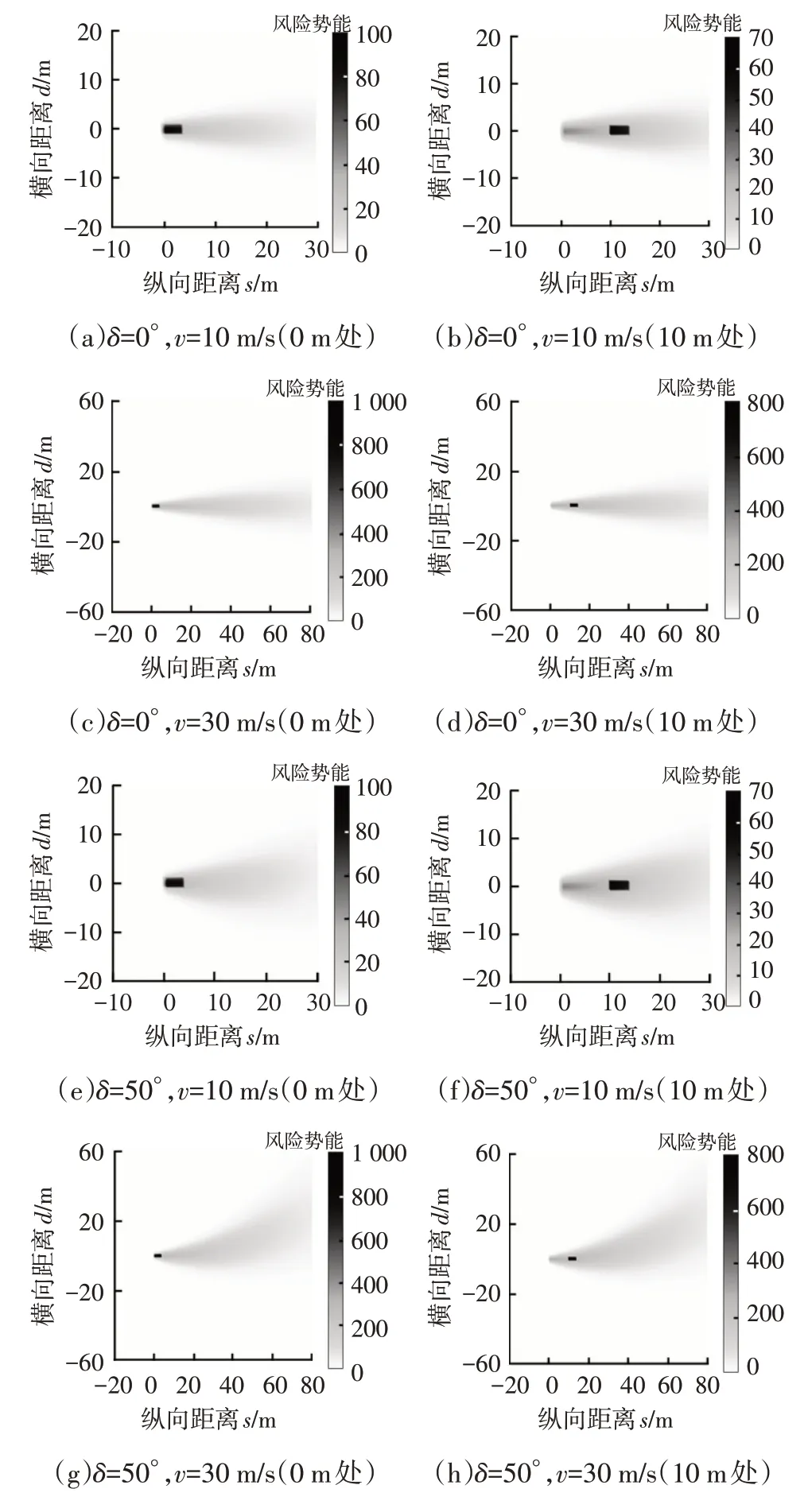
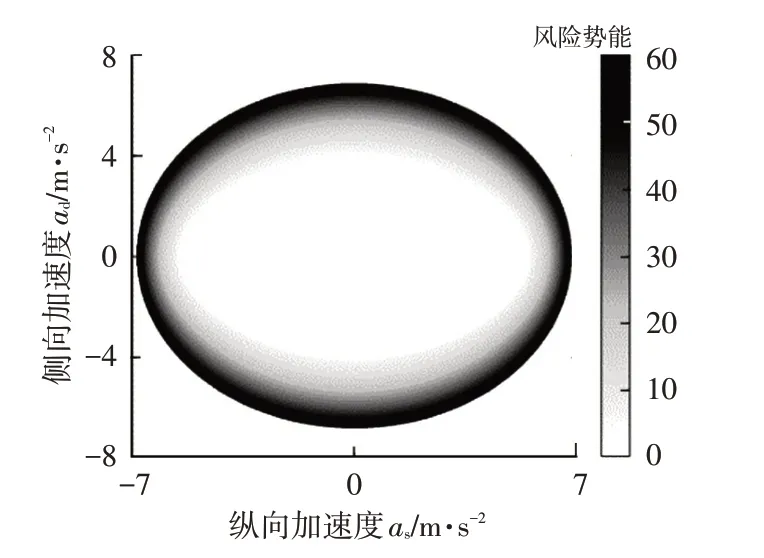
4.2 轨迹规划
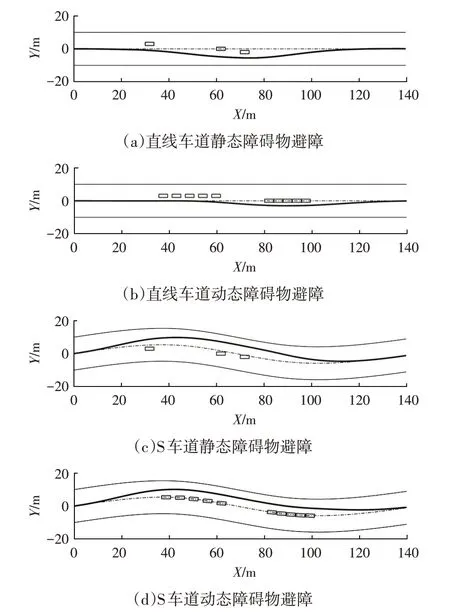
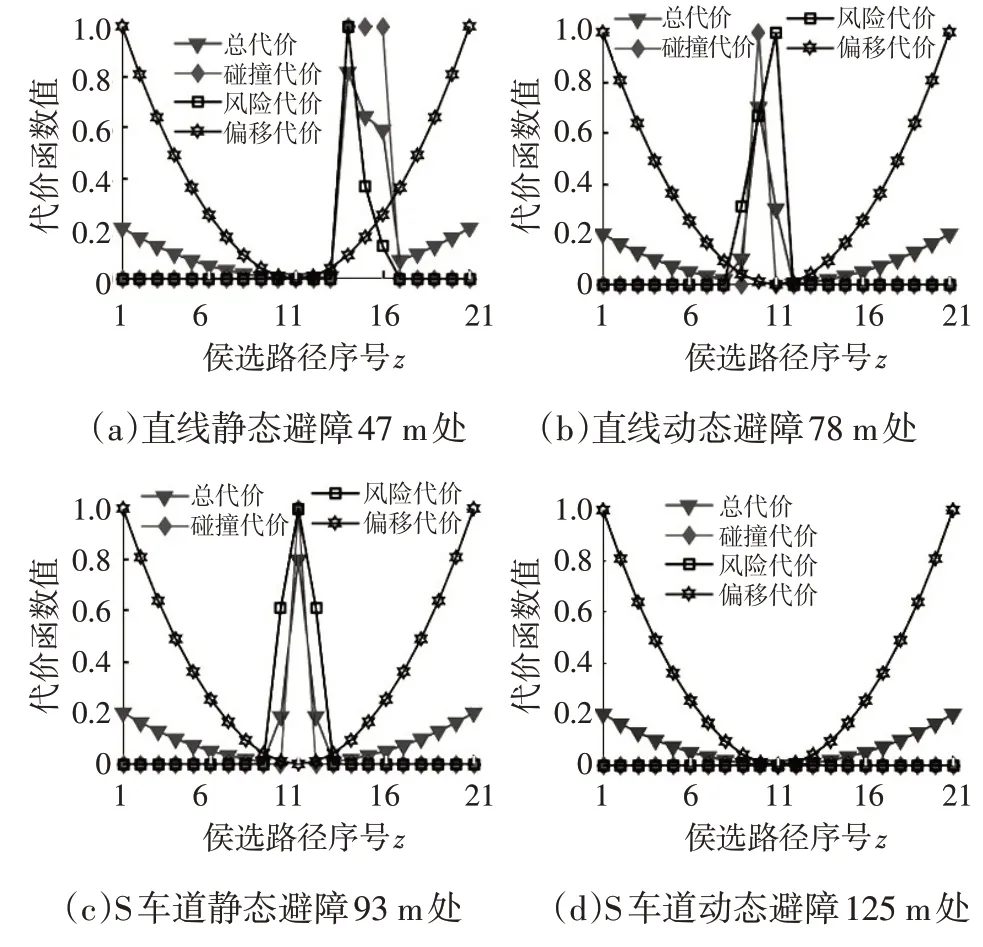
4.3 测试验证

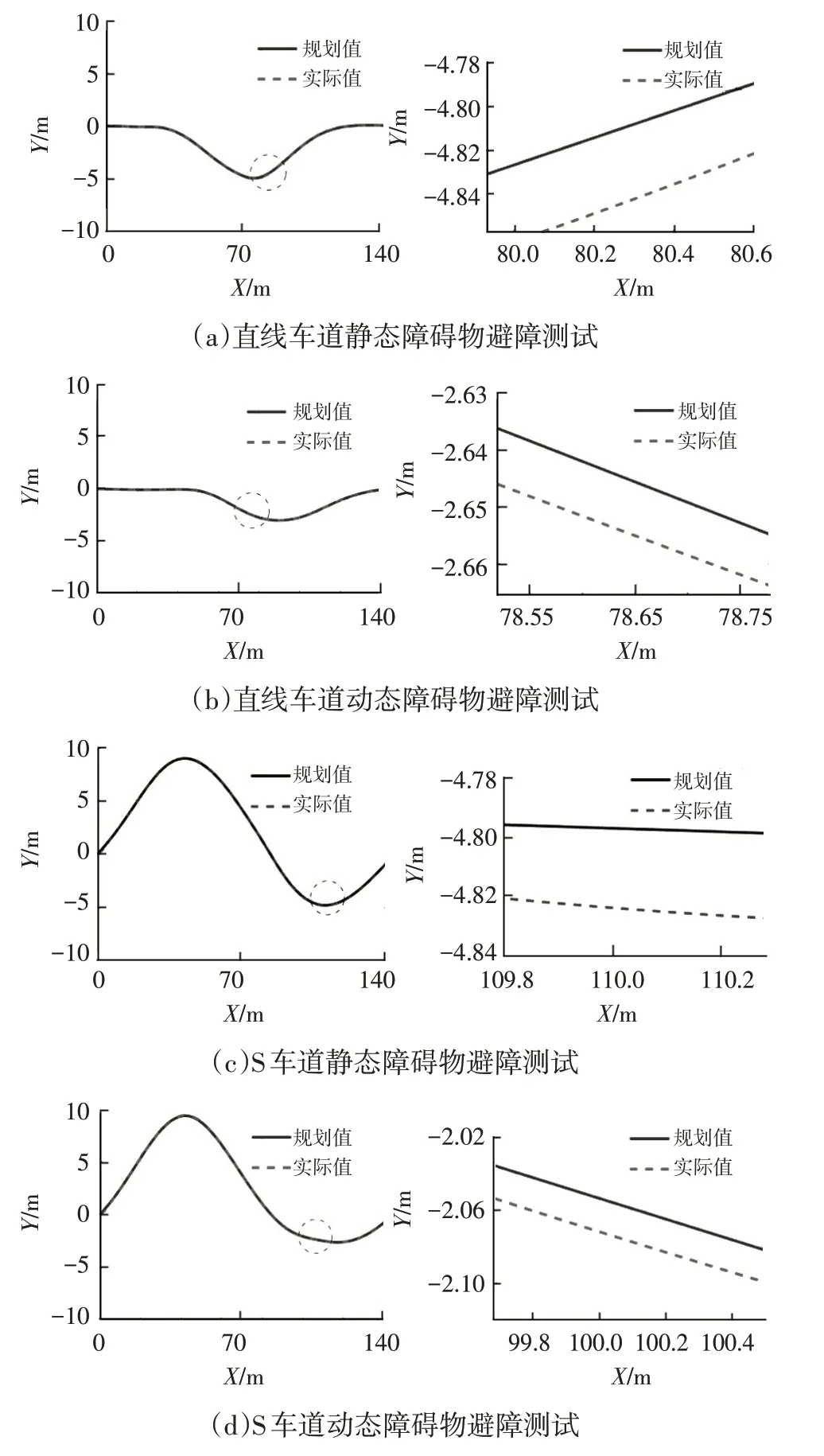

5 结束语
——《势能》

