基于等效渗透系数法修正的多节点井流模型

牛赟凯,王全荣

(中国地质大学(武汉)环境学院,湖北 武汉 430078)

管道是含水层中十分常见的水文地质结构,包括自然条件下的岩溶管道、动物的洞穴、虫孔,也包括人为的管道,如人工挖掘的水平井、隧道和探矿巷道等。由于管道与周围的介质在渗透性方面具有较大的差异,这些管道的存在使含水层呈现高度非均质性,因此成为管道-孔隙双重介质系统,其中高渗透的管道是一个系统,低渗透的孔隙或裂隙基质是一个系统,导致地下水流场的模拟十分困难[1]。随着工业化进程的不断发展,面对日益复杂的地下水环境变化,一个良好的管道流模型是研究地下水污染物迁移[2]、巷道涌水[3]等环境安全问题的基础,对进一步刻画含水层复杂的地质环境与渗流场具有十分重要的意义。

目前,针对含水层中不同类型的管道流,已经开发了许多数值模型,包括等效渗透系数模型、多节点井流(multi-node well,MNW)模型和管道流(conduit flow process,CFP)模型3种类型。陈崇希等[4-5]提出“渗流-管流模型”,该模型利用等效渗透系数法将管道处理为高渗透介质,并将沿水流方向的渗透系数设置得很大,其取值基于不同流动状态下管道流模型计算的等效渗透系数;Halford等[6]和Konikow等[7]基于MODFLOW软件平台开发了MNW模型,该模型为不同网格中的管道按序分配节点,将所有节点处理为一个连通的管道,再利用三维地下水流动方程来计算含水层介质网格的水头,则管道中水头可利用含水层介质网格水头加管道中水头损失项来进行计算。多节点井流模型分为MNW1模型及其修订版本MNW2模型,两者的算法相同,其中MNW2模型较MNW1模型改善了对非垂直井与非完整井的模拟效果,并可以根据指定的泵性能(扬程-容量)曲线对流量进行调整,扩充了MNW模型的适用范围。如:Shoemaker等[8]在MODFLOW软件中加入了管道流模块CFPv1;Reimann等[9-11]和Kavousi等[12]后续扩展了管道流(CFP)模型的应用范围,将其升级为CFPv2改进程序,加入了管道抽水、溶质与热的转输等功能,为含水层中地下水管道流的模拟研究提供了更丰富的场景。CFP模型采用管道-孔隙双介质系统,利用有限差分法将多孔介质含水层处理为矩形网格,将离散管道节点嵌入含水层网格模型中,使用Hagen-Poiseuille方程[13]或结合Colebrook-White公式的Darcy-Weisbach方程[14]计算含水层管道中的地下水流量,并使用三维地下水流动方程计算含水层中的层流,最后通过管道边界将交换流量耦合在一起。

MNW模型在进行含水层中地下水管道流求解时,采用管道节点所处网格的渗透系数进行运算[6],在模拟中一般假设存在管道的含水层介质网格渗透系数为孔隙介质渗透系数,实际上,由于管道具有贯通性与高水力传导性能,含水层的水力传导能力将受到管道几何形状与分布状态的影响[15-19]。管道占据有限差分网格一定空间,管道-含水层网格系统具有很强的非均质性,使管道-含水层网格的整体渗透系数不能按照孔隙介质的渗透系数处理,其取值应大于孔隙介质的渗透系数。等效渗透系数法可以定量计算并概化不同管道流动状态下含水层的平均等效渗透系数,为CFP模型及在MODFLOW软件中进行含水层中地下水管道流与层流计算提供了渗透系数选取的理论依据。

因此,对于MNW模型中的管道网格渗透系数取值问题,本研究采用MNW2版本的多节点井流模型和CFPv2版本的管道流模型,利用等效渗透系数法修正多节点井流模型,并基于室内二维砂槽管道流试验对修正后的多节点井流模型的模拟结果与管道流(CFP)模型模拟流场、实测流场进行了对比分析,为寻找更加准确而高效的含水层中地下水管道流数值模拟方法提供参考。

1 基于MODFLOW的含水层中地下水管道流数值模拟方法

1.1 等效渗透系数模型

由于管道的渗透性显著高于含水层孔隙介质的渗透性,因此需要为管道设置一个较大的渗透系数,将管道系统等效为高渗透介质系统。管道的渗透系数取值与管道中地下水的流动状态有关。

在层流状态下,当管道流的雷诺数Re<2 300时,管道的等效渗透系数表达式如下:

(1)

式中:Kn为管道的等效渗透系数[L/T];d为管道直径[L];γ为流体容重[M/L3];μ为流体动力黏滞系数[M/LT]。

在紊流状态下,管道的等效渗透系数表达式为:

(2)

式中:g为重力加速度[L/T2];f为摩擦系数[无量纲];v为流体流速[L/T]。

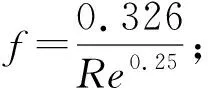
管道在含水层网格中的示意图,如图1所示。

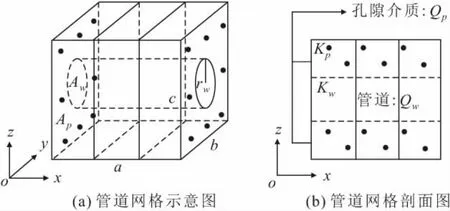
图1 管道在含水层网格中的示意图Fig.1 Diagram of a conduit in aquifer grid

由于等效渗透系数法揭示的含水层中地下水管道流动规律在形式上与达西定律一致,因此在管道截面积小于含水层孔隙介质网格面积时,可利用达西定律与质量守恒定律计算管道网格的平均等效渗透系数[20-21]。在图1中,Aw为管道截面面积[L2];Ap为含水层孔隙介质网格面积[L2];Kw为管道等效渗透系数[L/T];Kp为含水层孔隙介质渗透系数[L/T];Qw为管道流量[L3/T];Qp为孔隙介质流量[L3/T]。

若假设管道网格的平均等效渗透系数为Kavg,则有:

(3)

若网格剖分与管道截面一致,则可忽略含水层孔隙介质项KpAp,使

Kavg=Kw

(4)

该方法要求依据管道流不同流动状态来计算相应的等效渗透系数并赋值,若由于资料问题管道的等效渗透系数难以计算,可以初步赋予一个较大的渗透系数,在后续模型验证的过程中将模拟值与实测值进行对比校准,以调整管道的等效渗透系数。

1.2 MODFLOW-CFP模型

MODFLOW-CFP模型的优势在于能够较详细地刻画管道在含水层中的分布形态与几何特征,是目前使用最广泛的含水层中地下水管道流模拟程序。该模型采用管道-孔隙双重介质系统,孔隙介质含水层系统采用MODFLOW程序模拟,管道系统采用CFP模块模拟,两者之间的水量交换通过源汇项的方式加入各自的计算方程中。

根据质量守恒定律建立管道内的水量平衡方程,用于计算网格水头与管道水头的差值:

(5)

式中:Qip为第i段管道的流量[L3/T];Qex为交换流量[L3/T];QR为外源补给/排泄流量[L3/T];Qs为管道中的含水层与管道之间的储量变化[L3/T],当管道为承压状态时,管道节点储蓄量变化为0,可不计入公式。

管道流量公式采用Hagen-Poiseuille方程与结合Colebrook-White公式的Darcy-Weisbach方程。Hagen-Poiseuille方程中,管道两端的水头损失是由于管道中层流存在自身的流动阻力造成的,流动阻力与液体黏滞系数有关;Darcy-Weisbach方程中考虑了管道壁的粗糙性。

含水层与管道之间的交换流量Qex可表示为:

Qex=αi,j,k(hin-hi,j,k)

(6)

式中:αi,j,k为i、j、k网格单元中含水层系统与管道系统的交换系数[L2/T];hin为第i段管道的水头[L];hi,j,k为i、j、k网格单元中含水层的网格水头[L]。

含水层与管道之间的水量交换通过其交换系数αi,j,k来控制,其计算公式为:

(7)

式中:(Kw)i,j,k为含水层i、j、k网格单元的渗透系数[L/T];Δlip为第i段管道长度[L];dip为第i段管道直径[L];τip为第i段管道粗糙度[无量纲];rip为第i段管道半径[L]。

1.3 修正的多节点井流模型

MNW模型在有限差分网格中根据管道分布按序分配节点,将所有节点作为整体,处理为一个连通的管道,水流在通过管道运动的过程中会产生多项水头损失[6],该模型考虑了水流在管道中运动的部分水头损失,因此在对含水层中地下水管道流的模拟上能够更加精确地刻画管道水头。

MNW模型采用一个通用的水头损失方程来计算含水层网格水头与管道水头的差值:

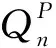
(8)

式中:hwell为管道水头[L];hn为含水层中地下水网格水头[L];Qn为第n个管道节点的流量[L3/T];A为线性含水层水头损失系数[T/L2];B为线性水头损失系数[T/L2];C为非线性水头损失系数[TP/L(3P-1)];P为非线性流量的幂。

公式(8)表明,管道的水头等于管道所在含水层网格水头(hn)加上几个水头损失项。在MODFLOW软件中使用有限差分法求解地下水流动偏微分方程,获得hn[22]。

第一个水头损失项(AQn)描述了由于管道的半径小于井所在单元的尺寸而导致的含水层水头损失。在忽略表皮效应和局部紊流效应的情况下,公式(8)中含水层水头损失AQn可用Thiem稳态流动方程来表示:

(9)

式中:T=Kb为含水层的导水系数[L2/T](其中K为含水层的渗透系数[L/T];b为含水层的厚度[L]);ro为有限差分单元的有效半径[L];rw为管道的实际半径[L]。

公式(9)中计算含水层导水系数的含水层渗透系数为管道网格渗透系数,系数A的计算公式为

(10)

第二个水头损失项(BQn)是指在管道端点和筛管附近及内部发生的水头损失,系数B的计算公式为

(11)

式中:Skin为衡量表皮效应大小的无量纲表皮系数。

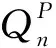
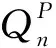
修正后的水头损失方程为

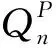
(12)

当监测数据不足时,无法计算相关系数,则可使用多节点井流模型中的“SPECIFYcwc”模式,利用MNW2模块中封装的网格到管道的水力传导系数(CWCn),手动赋予一个近似的初始值[6,23],并在后续模型验证的过程中将模拟值与实测值进行对比校准。

2 二维砂槽管道流数值模拟

为了对比修正前后多节点井流模型的模拟效果,本文以文献[24]、[25]中二维砂槽管道流试验为例,采用不同模型对二维砂槽管道流进行了数值模拟,并将水头模拟结果与实测结果进行了对比。具体参数如下:砂槽整体尺寸为57.8 cm×2 cm×26 cm(长×宽×高),管道直径为2 cm,位于砂槽底部,砂槽两侧为长5 cm的水箱,含水层规格为47.8 cm×2 cm×24 cm;承压含水层两侧为定水头边界,管道进水口为定水头边界;含水层为均质各向同性,含水层渗透系数为0.061 9 cm/s,含水层储水系数为2×10-5m-1,含水层初始水位为26 cm,左侧进水处定水头值为30 cm,右侧出水处定水头值为23 cm,管道进水口处定水头值为34 cm(图2)。整个试验时长为240 s。

图2 二维砂槽管道流试验装置与实测水头[24-25]Fig.2 Experimental device and measured head distribution for 2D sand tank pipeline flow[24-25]

根据砂槽形态构建二维砂槽网格模型,将三维砂槽网格模型剖分为22列×13行,不同区域分别表示含水层、管道和定水头装置(图3)。含水层网格从上至下12行,分为12层,从左至右分为20列,左右两侧各有一列宽5 cm的网格表示用于控制定水头边界条件的水槽,底部为直径2 cm的管道。含水层中水文地质参数和边界条件与试验相同,初始水头设置为26 cm。

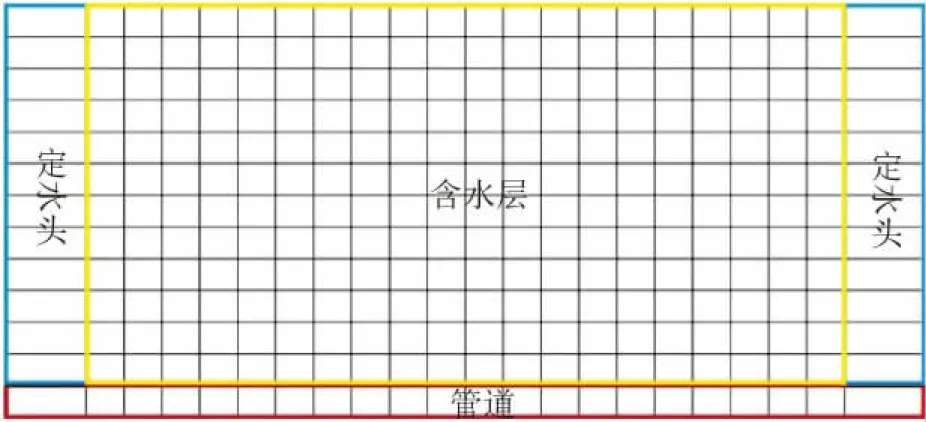
图3 二维砂槽网格模型示意图Fig.3 Schematic diagram of the 2D sand tank grid model

采用MODFLOW-CFP模型对二维砂槽管道流进行数值模拟时,在砂槽网格模型第13层插入22个节点控制一条管道,管道网格采用孔隙介质渗透系数。管道模型中,管道弯曲度为1,假设管道光滑,粗糙度设置为0.000 000 1;管道流的雷诺数Re采用经验值,下界雷诺数设计为2 000,上界雷诺数设计为4 000;在管道系统中将进水口与出水口设置为定水头,管道系统与含水层网格系统的交换系数αi,j,k由MODFLOW程序通过管道形态与含水层渗透系数自动计算。通过数值模拟后,可得到CFP模型的模拟流场。

采用MNW模型对二维砂槽管道流进行数值模拟时,在砂槽网格模型第13层插入22个节点控制一条管道,管道网格采用孔隙介质渗透系数,并将管道外源补排项的值设为0 m3/s,不考虑表皮效应。经调试发现,调整系数C与P对模拟结果的影响并不显著,尝试在多节点井中额外加入外源流量注入或排泄后,参数的调节对流场有较大的影响,这表明在该定水头边界条件下,管道节点之间的流量较小,管道中的紊流水头损失很小。

由于管道与附近含水层水头差的变化较含水层中水头差的变化大,一般插值方法如最小二乘法、三角剖分法等得到的流场线不平滑或波动极大,插值标准误差高,与流场的实际情况差距较大,而经测试后发现,克里金插值法得到的流场线自然平滑,且插值标准误差低于0.05,优于其他插值方法,准确度较高,因此本文将二维砂槽管道流试验流场中的实测水头值使用Surfer进行克里金插值,重新绘制得到水槽中的整体流场,并将CFP模型和MNW模型的模拟流场做同样处理,得到原始MNW模型和CFP模型的模拟流场与实测流场的对比结果,如图4所示。

图4 原始MNW模型和CFP模型模拟流场与实测流场 的对比图Fig.4 Comparison of simulated flow field using original MNW model and CFP model with experimental flow field

由图4可知:原始MNW模型的模拟结果并未表现出含水层中存在双重介质系统,管道中水头从左至右降低,与实测流场情况不符;CFP模型中管道表现高渗透性,其模拟流场与实测流场趋势相同,砂槽内水头中部高,向两边减小,而原始MNW模型的模拟结果与其拟合程度较差。

数值模型的模拟流场与实测流场的误差,可采用均方根误差(RMSE)进行量化分析,其计算公式如下:

(13)

式中:M为实测水头点位个数;hi实测值为实测点i的水头[L];hi模拟值为实测点i的数值模拟水头[L]。

经误差分析可知,原始MNW模型模拟水头与实测水头的RMSE值为2.516 8 cm,整体误差水平较大;CFP模型模拟水头与实测水头的RMSE值为0.925 8 cm,其模拟效果优于原始MNW模型。因此,在原始MNW模型的基础上,利用等效渗透系数对模型进行修正,即将管道节点处有限差分网格的渗透系数由孔隙介质渗透系数修正为等效渗透系数。在试验中,管道中流量较小,可视作层流,根据公式(3)计算得管道层流等效渗透系数Kavg为12 129 cm/s。采用修正MNW模型对二维砂槽管道流进行了数值模拟,并将其模拟结果与CFP模型模拟流场和实测流场进行了对比,其结果如图5所示。

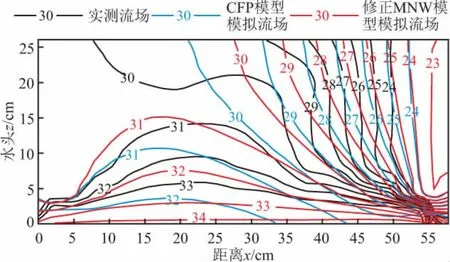
图5 修正MNW模型模拟流场与CFP模型模拟流场、 实测流场对比图Fig.5 Flow field comparison of modified MNW model with CFP model and experimental flow field

由图5可知:原始MNW模型经过等效渗透系数法修正后,修正MNW模型很好地表现出管道的存在使含水层产生了非均质性,管道与含水层之间的水量交换增加,含水层水头值抬升,模拟结果趋近实测流场;修正MNW模型相较CFP模型的管道表现出更强的渗透性,由于定水头边界的影响,管道中水头处处相同,处于承压状态,采用修正MNW模型模拟得到的含水层整体水头高于CFP模型模拟值。

经误差分析可知:修正MNW模型模拟水头与实测水头的RMSE值为0.591 4 cm,小于CFP模型模拟水头与实测水头的RMSE值0.925 8 cm,表明修正MNW模型的模拟效果更好;与未修正MNW模型对比,模拟水头与实测水头的RMSE值由2.516 8 cm减小为0.591 4 cm,模拟误差降低了76.14%,说明修正MNW模型的模拟效果得到了大幅度提升。

3 结 论

1) 对于含水层中的管道,在MODFLOW软件中使用有限差分法进行数值模拟时,其存在会影响管道网格渗透系数的取值,进而影响模拟精度。管道中流量较小的情况下,原始MNW模型并不能很好地展现管道的高渗透性质。根据等效渗透系数法修正MNW模型,对比CFP模型模拟流场,修正MNW模型的模拟结果优于CFP模型;对比实测流场,修正MNW模型的模拟结果趋近于实测流场,相较原始MNW模型误差降低了76.14%。

2) 修正MNW模型综合考虑了高渗透管道的存在对有限差分网格渗透系数取值的影响,能够更好地体现管道与含水层的双重介质性,经等效渗透系数修正后,管道-含水层网格系统的渗透系数增加,水流在管道中运动的水头损失降低,管道与含水层介质中的水头差增加,水流交互更加显著。若管道内水头高于含水层中水头,MNW模型在耦合等效渗透系数后会进一步抬升含水层中水头,反之则降低。

3) 本研究中管道内的水体流态为层流,理论上MNW模型在刻画紊流带来的水头损失上更具优势,该修正MNW模型对管道流紊流状态的模拟效果还需要进一步验证。