两种入水角对卷式膜组件内部流动和流场的影响

孙思昌,范 茏,刘 峤,王 青,徐 农,董 强

卷式膜组件又称螺旋卷式膜组件,可以有效去除溶剂中盐分和小分子有机物,已广泛应用于纯水与超纯水制备、饮用水净化、海水淡化、废水处理、工业流体分离与浓缩等领域[1]。它利用卷式膜两侧的化学势梯度作为超滤、反渗透、渗透汽化等分离过程的推动力,推动溶液中不同组分在卷式膜内部的跨膜运动,在流场中实现液体混合物的分离,因此了解卷式膜内物理量的流场分布和流动特性,可以提高传质推动力、降低阻力,获得较好的分离效果并减少能耗,进而助力国家“双碳”目标的达成。

计算流体力学(Computational Fluid Dynamics, CFD)是研究膜组件内流体力学特性的主要方法[2],它对于复杂的计算域、物理模型和实验条件都具有很好的适应性,可以满足模拟复杂通道内流体流动的需求,对膜组件的设计与优化具有重要意义。米文强等[3-4]对卷式膜的三种隔网排列方式进行比较,通过二维模拟发现之字型和浸没型排列方式优于空腔型。康志雄等[5]采用选择透过性壁面模拟渗透汽化过程,对入水角度、雷诺数、隔网厚度等参数进行了分析讨论。郭中权等[6]通过对矿井水脱盐过程的模拟,预测了卷式膜组件内的流动、无机盐浓度分布、膜表面的浓差极化以及不同操作条件下膜结垢的倾向[7-8]。Cao 等[9]通过溶解-扩散理论建立数学模型,对膜技术分离苯/苯乙烯的效果进行了预测,并讨论了相关参数对分离效果的影响。Ranade 和Kumar[10]对膜通道内的流动进行了 CFD 模拟,探究不同类型的隔网对流动的影响。以上文献均对卷式膜组件两维(2D)、三维(3D)的模型结构进行了模拟,但主要集中在膜组件隔网的设计和排布,少有文献涉及隔网入口与入水角度。

本文对80 ℃时,95%的乙醇/水溶液通过PVA(Polyvinyl Alcohol,聚乙烯醇)卷式膜组件的流动,分别在3D和2D下进行CFD模拟,探讨了两种不同入水角对卷式膜组件内速度、壁面剪切应力、压降等参数的影响,所获的结果对卷式膜的优化设计与工艺操作有一定的参考意义和指导作用。

1 模型及模拟方法

1.1 数学模型

采用Ansys Fluent 2020 R2对卷式膜组件内乙醇与水混合溶液的流动分别进行了3D和2D的模拟,假设流体为不可压缩牛顿流体[8-10],采用纳维-斯托克斯(Navier-Stokes)方程描述流体流动,假设流动为层流,在非稳态下计算[11-14]。选用组分运输方程模拟浓度。由于重力场对膜的传质作用影响不大,因此不考虑重力影响[15-16]。

1.2 边界条件和计算方法

Fimbres-Weihs等[8]认为,当雷诺数超过临界值1534.6时,能耗会呈指数增长,当Re在526.0和841.0之间,溶液在膜内的流动由稳态转变成非稳态,压降与雷诺数呈正比变化。为更好地比较,本文选取与文献[4]相同的雷诺数,即Re=800.0。95%的乙醇/水溶液的粘度为1.65×10-5kg/(m·s)。

雷诺数:

(1)

式中,dh、u、ρ、μ分别为水力直径、平均入口流速、密度及粘度。

水力直径定义:

dh=4(VTOT-VSP)/(SC+SSP)

(2)

其中VTOT为流道体积(不包括隔网),VSP为隔网体积,SC为流道表面积,SSP为隔网表面积[7]。

边界条件入口采用速度入口,速度值根据雷诺数计算获得。出口采用压力出口。由于膜内的流速可以达到5m·s-1以上,而膜的传质通量较小,与流速的数量级相差较大[17-18],并不会影响膜的主体流动,因此,将膜面与隔网表面都设置为不可渗透的壁面。压力速度耦合采用SIMPLE算法。残差取为10-5。

1.3 3D模型的建立

选用入水角为45°(即入水角度与上层隔网成45°)的非交织型隔网建立3D模型,模型的隔网结构存在柱面与膜面相切、柱面与柱面相切的情况,为了保证网格质量,略微增大d的值,使相切变成相交[3],如图1所示。x轴正方向记为流道方向,y轴正方向为膜通道的高度,z轴方向与流道相垂直,主流道长20.0 mm,与主流道方向相垂直的方向长度也为20.0 mm,且Δl/h=3.0,d/h=0.5(Δl为相邻隔网间距,h为膜通道高低,d为隔网直径),如表1所示。

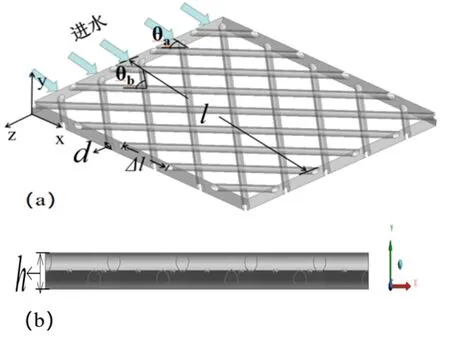
(a)侧视图;(b)正视图图1 3D隔网模型注:θa为进水流动方向与上层隔网的夹角,θb为上层隔网与下层隔网之间的夹角。

表1 模型的几何参数

采用非结构型四面体划分网格,共建立约300万网格[9],如图2所示。

2 结果与讨论

2.1 3D模拟结果

2.1.1 模拟结果的验证

为验证本模拟的准确性,将本模拟结果与文献[4]的模拟结果进行比较。

(1)速度的比较

在y轴上选取多个截面,求取各截面平均速度,与文献[4]进行比较,如图3所示。速度沿着y轴先增大后减小,且关于膜通道高度的中间截面y=0.5 mm对称。速度在越过隔网时达到最大,在隔网的两侧亦呈现出对称的趋势。本模拟与文献[4]趋势一致,最大误差为7.8%,证明本模拟的可靠性。

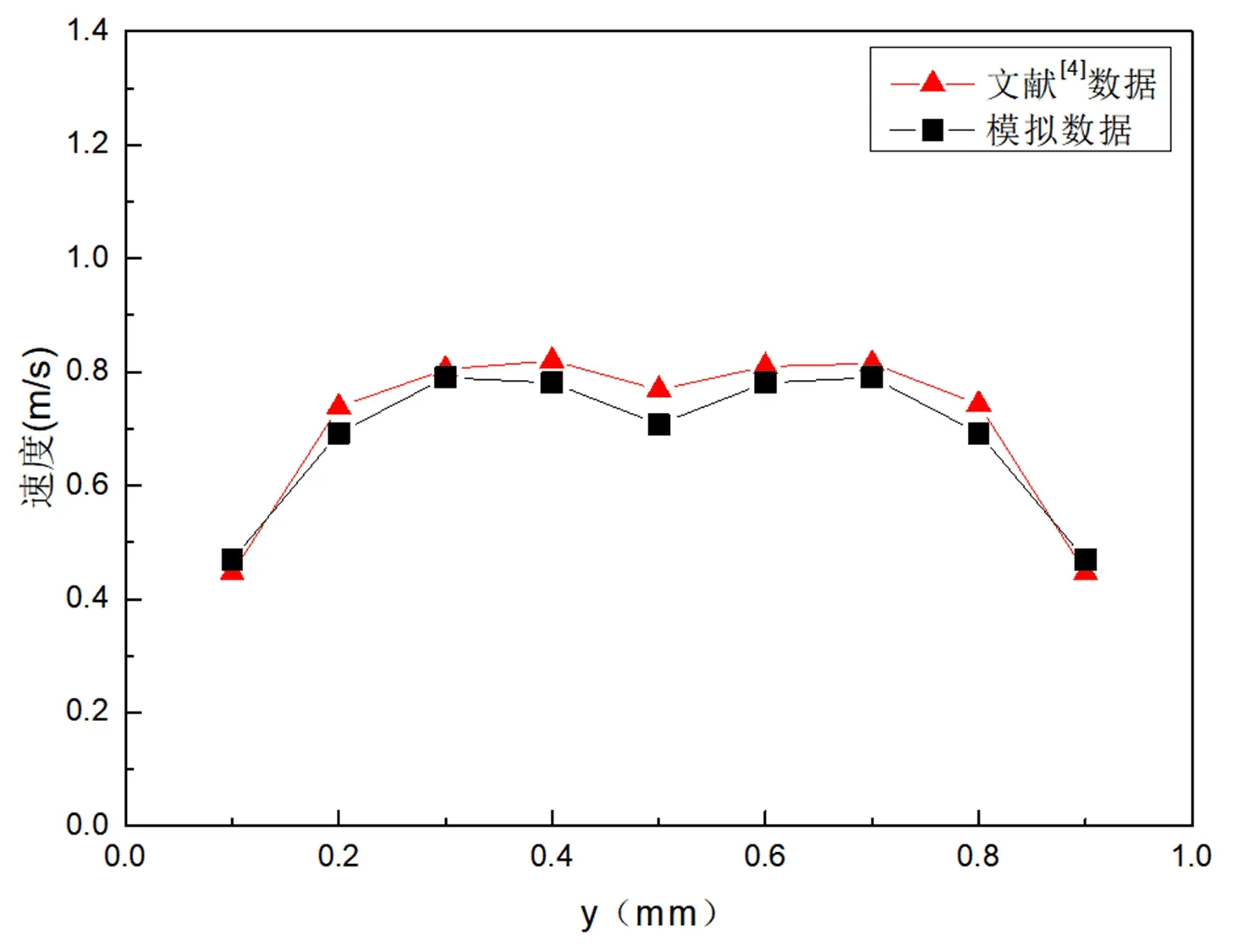
图3 沿y轴方向速度的比较

(2)壁面剪切应力比较

上、下壁面剪切应力与文献[4]数据的比较如表2所示。在不考虑重力的情况下,上、下壁面剪切应力大小相同,本模拟与文献[4]数据的最大误差为12.73%,再次证明本模拟方法和结果的可靠性。

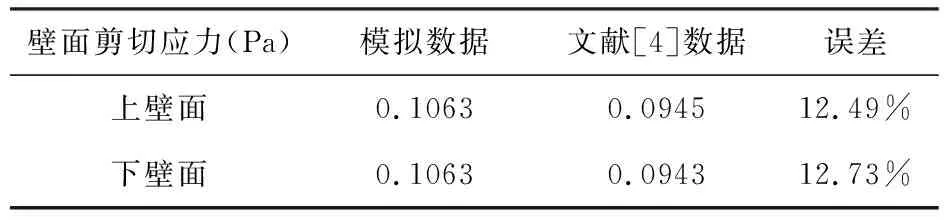
表2 平均壁面剪切应力

2.1.2 入水角度的影响

为探究卷式膜内流场变化与入水角度之间的关系,选取入水角分别为0°与45°的隔网,对速度、壁面剪切应力和压降进行比较。

(1)入水角对速度的影响

图4(a),4(b)所示分别为入水角为0°与45°时x-y截面的速度矢量图。流体经过隔网时,速度变大,流动过程中隔网对流速有一定影响,相较于45°入水角(图4(b)),0°入水角隔网前后的流体速度差别更大(图4(a)),说明0°入水角时隔网对流动的阻碍效果较45°入水角更强烈。同时,0°入水角时隔网后有较大的速度死区,并有漩涡生成,造成回流,说明入水角为0°时流动分布劣于45°。

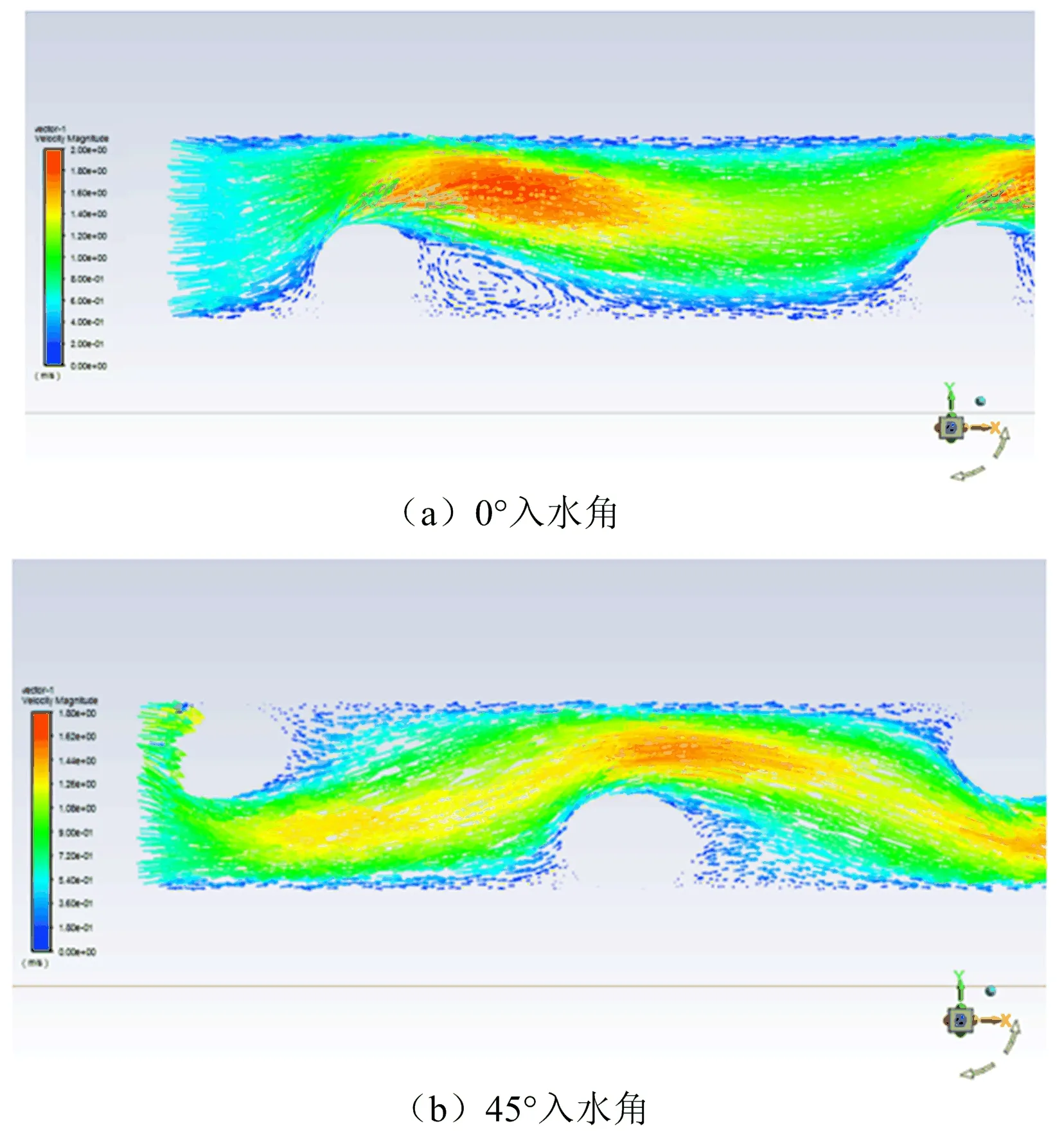
图4 速度矢量图

图4 速度矢量图入水角分别为0°与45°时,三个不同z截面(z=-2.0 mm,-10.0 mm,-18.0 mm)的速度云图如图5所示。0°入水角时,流速变化关于z=-10.0 mm截面对称,而45°入水角则关于z=-10.0 mm颠倒对称。因此,0°入水角时隔网下部靠近壁面的零速区很大,特别是z=-10.0 mm截面,上层隔网的下方出现大片的速度死区,会强化邻近壁面的浓差极化,易诱发出现大面积的膜污染。而45°入水角时零速区较少,减少了膜污染出现的可能性。

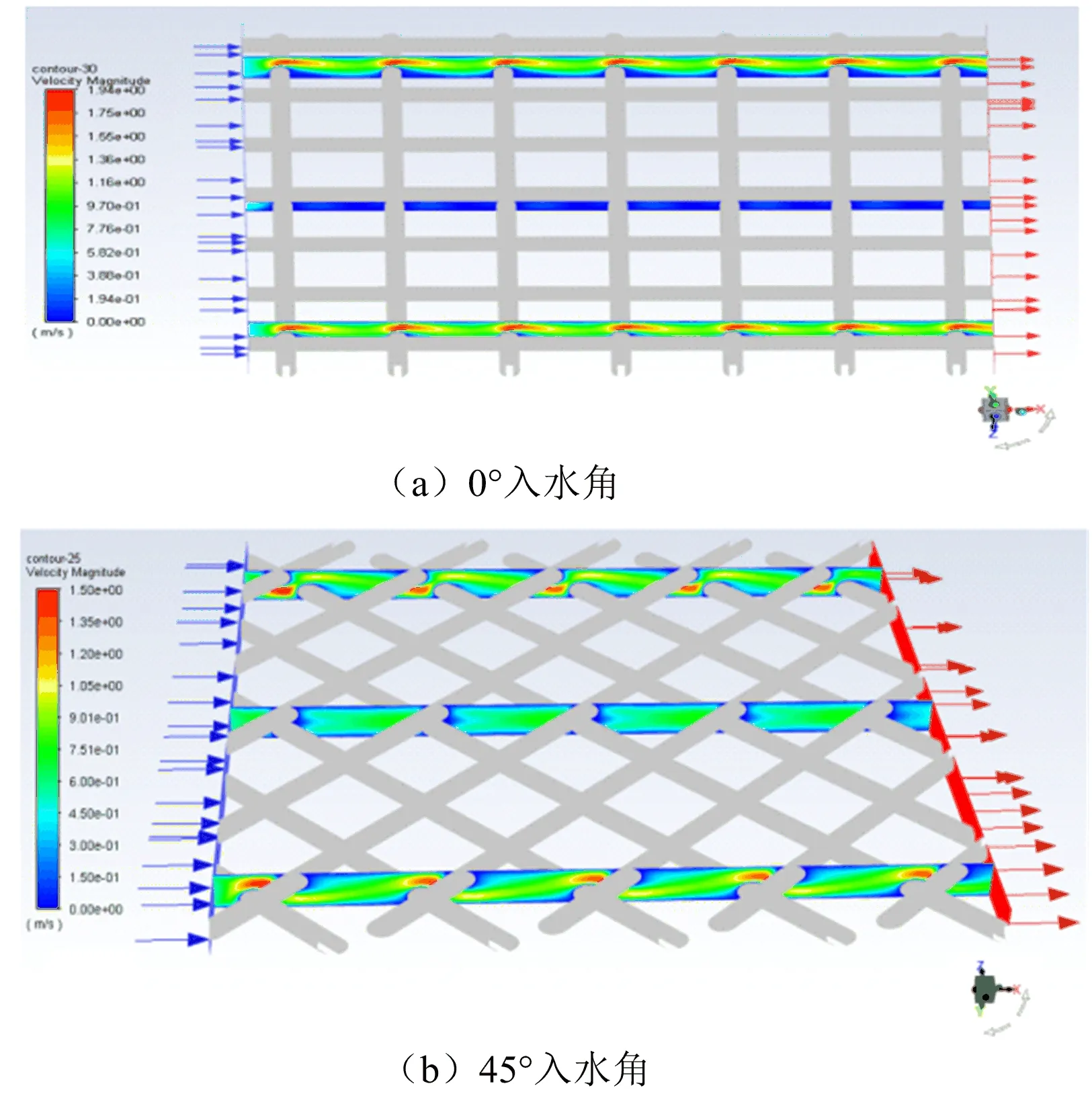
图5 z截面的速度云图

三个x截面(x=2.0 mm,10.0 mm,18.0 mm)的速度云图如图6所示。0°入水角模型中,由于上层隔网与入水方向平行,上层隔网对膜内流动的影响很小,下层隔网阻碍作用较强,使得膜内流向单一,这也是导致0°入水角模型下层隔网处死区较大的主要原因。而45°入水角模型中上、下层隔网都对流体产生扰流作用,并且隔网与流体的角度均为45°,在不考虑重力的作用下,上、下层隔网扰流作用的贡献相同。

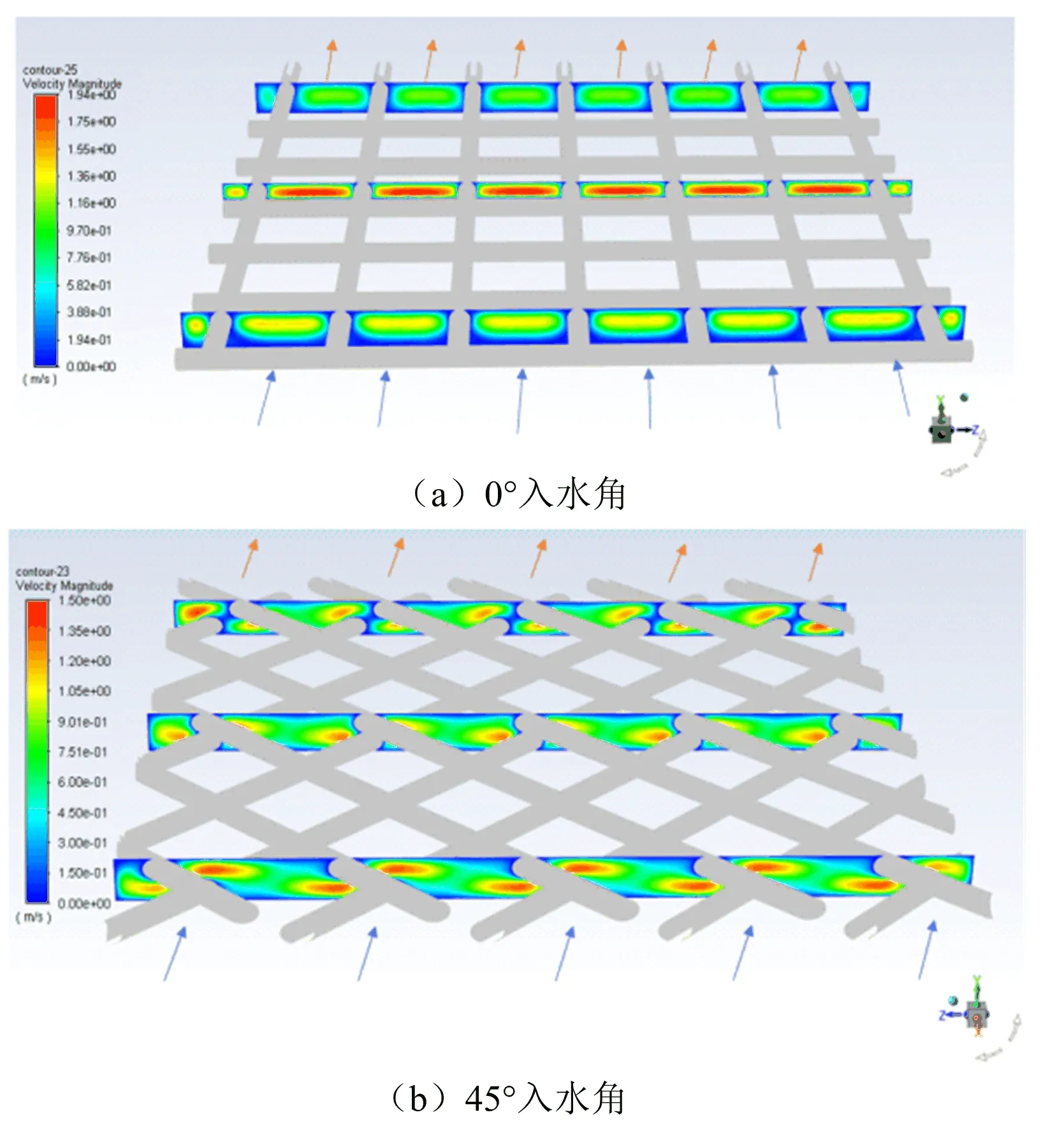
图6 x截面的速度云图

入水角为0°和45°时,分别求x=2.0 mm, 10.0 mm, 18.0 mm三个面在y方向的平均速度,获得各自随着y轴的变化,如图7所示。在入水角0°时,平均速度随着y轴的增大呈现出先增大后减小的变化趋势,变大区域都与上壁面接近,选取的三个截面最大速度差别较大,速度的差异受隔网位置的影响,越靠近下层隔网速度越大。x=10.0 mm截面的下部是隔网网丝的一部分,因此图7(a)中x=10.0 mm截面的速度曲线仅在x=0.6 mm之后产生数据。入水角45°时(图7(b)),三个截面的速度曲线都是呈现“m”型,即先增大后减小,且关于y=0.5 mm呈对称分布,三个截面的速度曲线比较接近,差别较小,这主要是由于入水角45°时各截面都会受到上、下隔网的共同影响。通过比较可以发现,入水角45°的隔网无论是在减小浓差极化、延缓膜污染还是在隔网内部的流动稳定性上都要优于入水角0°。

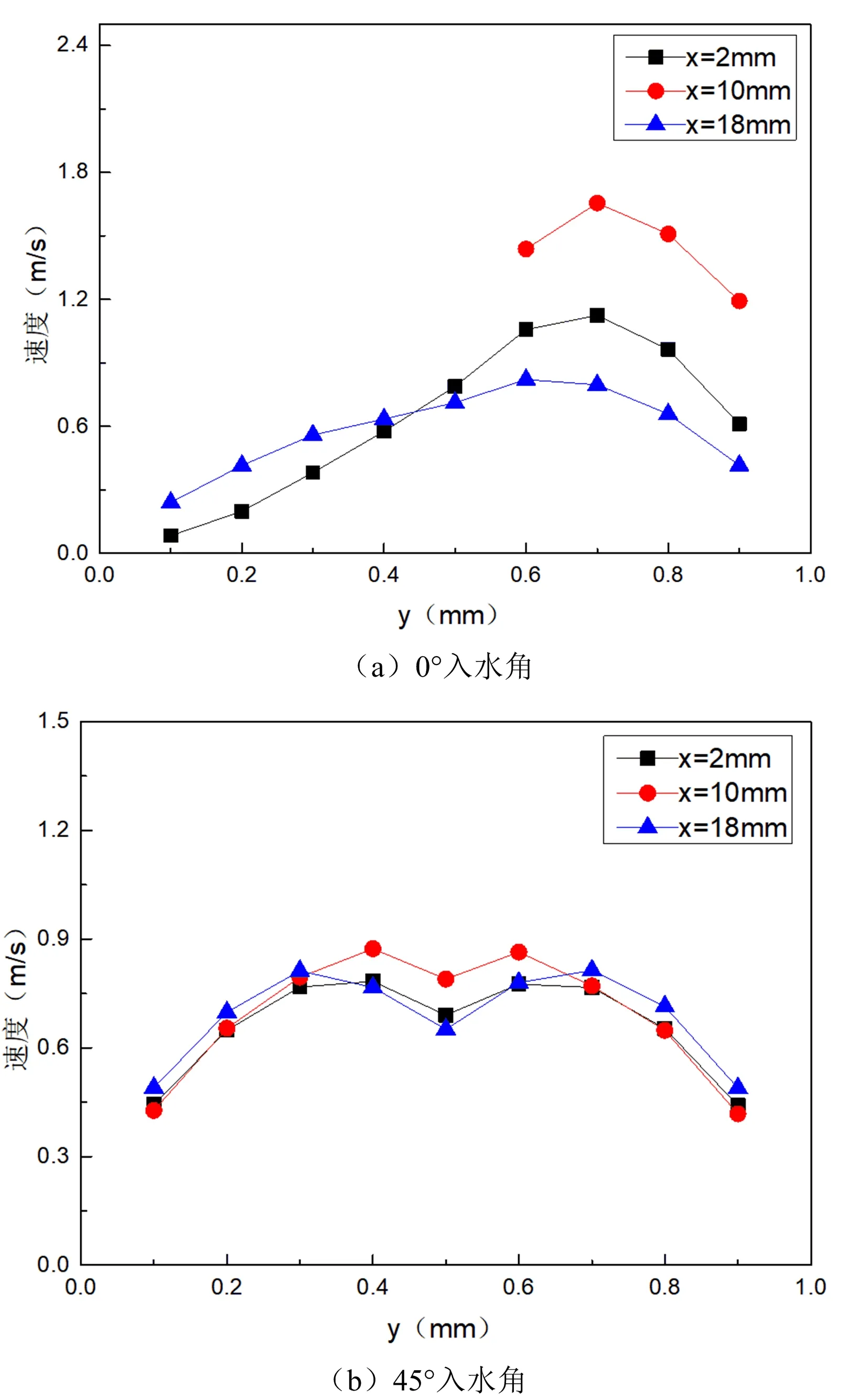
图7 速度曲线图

(2)壁面剪切应力

壁面剪切应力主要反映流体与膜面的接触情况,在膜面强度可以承受的范围内,壁面剪切应力越大意味着膜面的利用率越高[ 4,12]。如图8所示,0°入水角时上、下壁面剪切应力差距较大,且下壁面的剪切应力几乎为零,这也意味着0°入水角时下壁面的膜利用率较低。图9所示,45°入水角时上、下壁面剪切应力相差较小。将表3中0°与45°模型的上、下壁面剪切应力分别相加,可以发现45°入水角的壁面剪切总应力要大于0°入水角,即45°入水角时膜面的利用效率更高。且由于45°入水角模型的上、下壁面剪切相差较小,其模型所反映的操作稳定性也优于0°入水角。

图8 0°入水角壁面剪切应力图

图9 45°入水角壁面剪切应力图

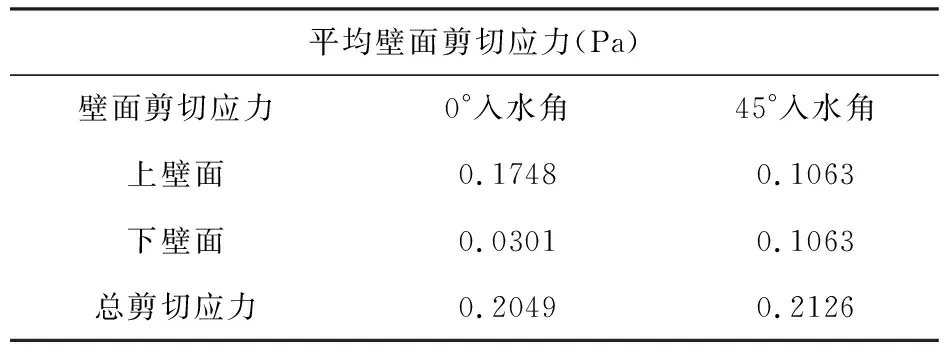
表3 平均壁面剪切应力

(3)压降

图10、图11所示为入水角0°和45°时,上下壁面的压降变化云图,两图的压降变化明显不同,二者的比较如图12所示。沿x轴方向, 0°入水角时压降呈阶梯状下降,且经过隔网时下降剧烈,而45°入水角时压降呈平缓的线性下降,这主要是由于45°入水角时隔网上、下层分布一致,且有一定的对称性,使得经过隔网的压力变化相对平缓。由于压降与能耗密切相关, 0°入水角模型内流体经过隔网时,压降下降较大,其消耗的能量也就大,而45°入水角时压降下降平缓,消耗的能量也较小。因此,比较能耗,45°入水角也优于0°入水角。

图10 0°入水角压降云图

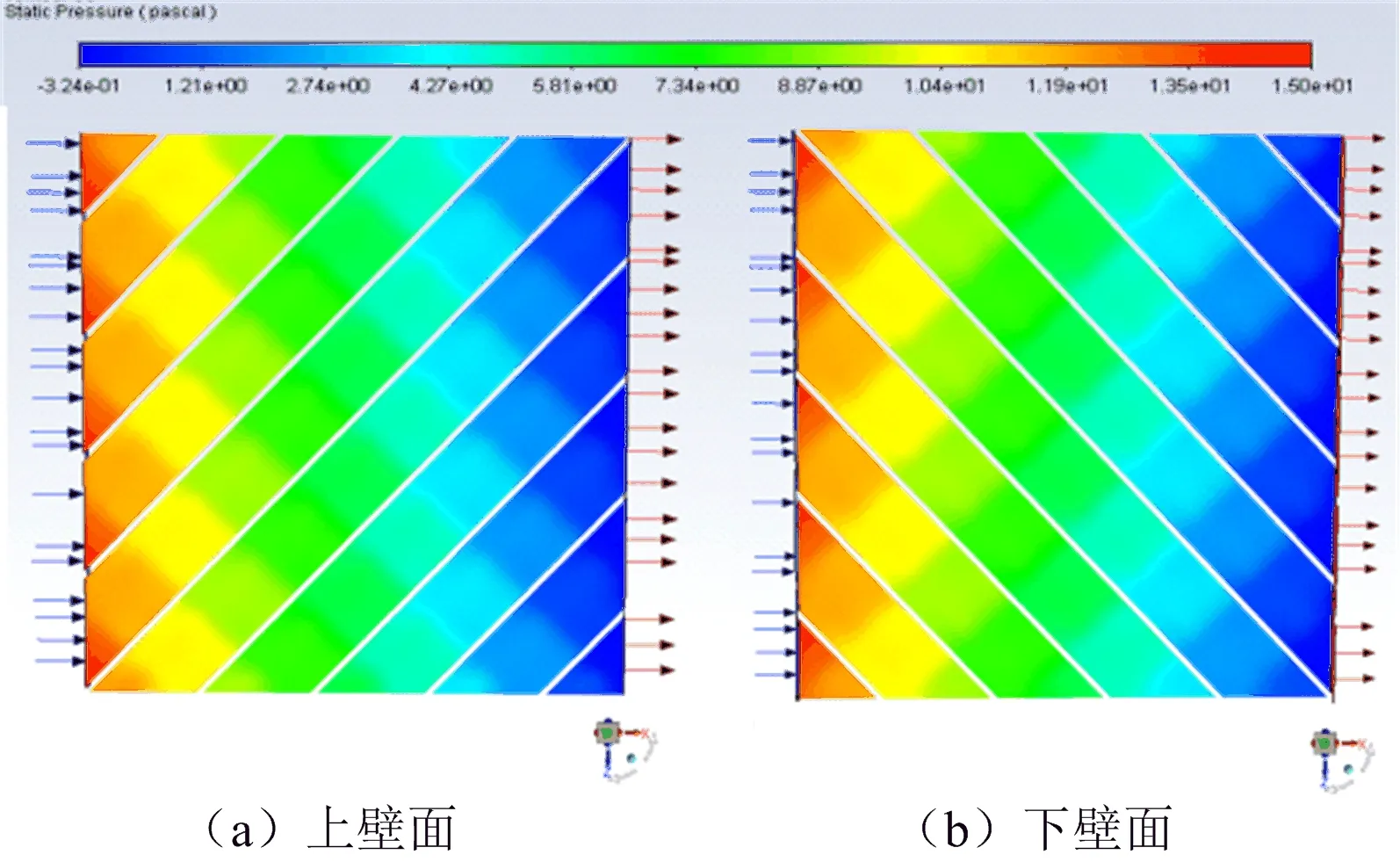
图11 45°入水角压降云图

图12 压降曲线图

对于卷式膜而言,综合考虑降低膜污染、提高膜面利用率、降低能耗等因素,入水角45°设计均优于入水角0°。

2.2 与2D模拟的比较

将3D模型简化为2D模型同样进行了模拟。采用非结构化网格,建立12层网格边界层用以检测流体边界层的流动,如图13所示。2D模型采用与3D模型相同的条件进行模拟,并与3D模拟中较优的入水角45°结果进行比较。

图13 2D模型网格划分示意图

(1)速度场比较

模拟的2D速度场如图14(a)所示。与3D模拟所得速度云图(图14(b))比较,当流体到达隔网时速度均会变大,翻越隔网后速度均变小,隔网的两侧均有死区。但2D模拟在隔网前后的死区面积明显大于3D结果。

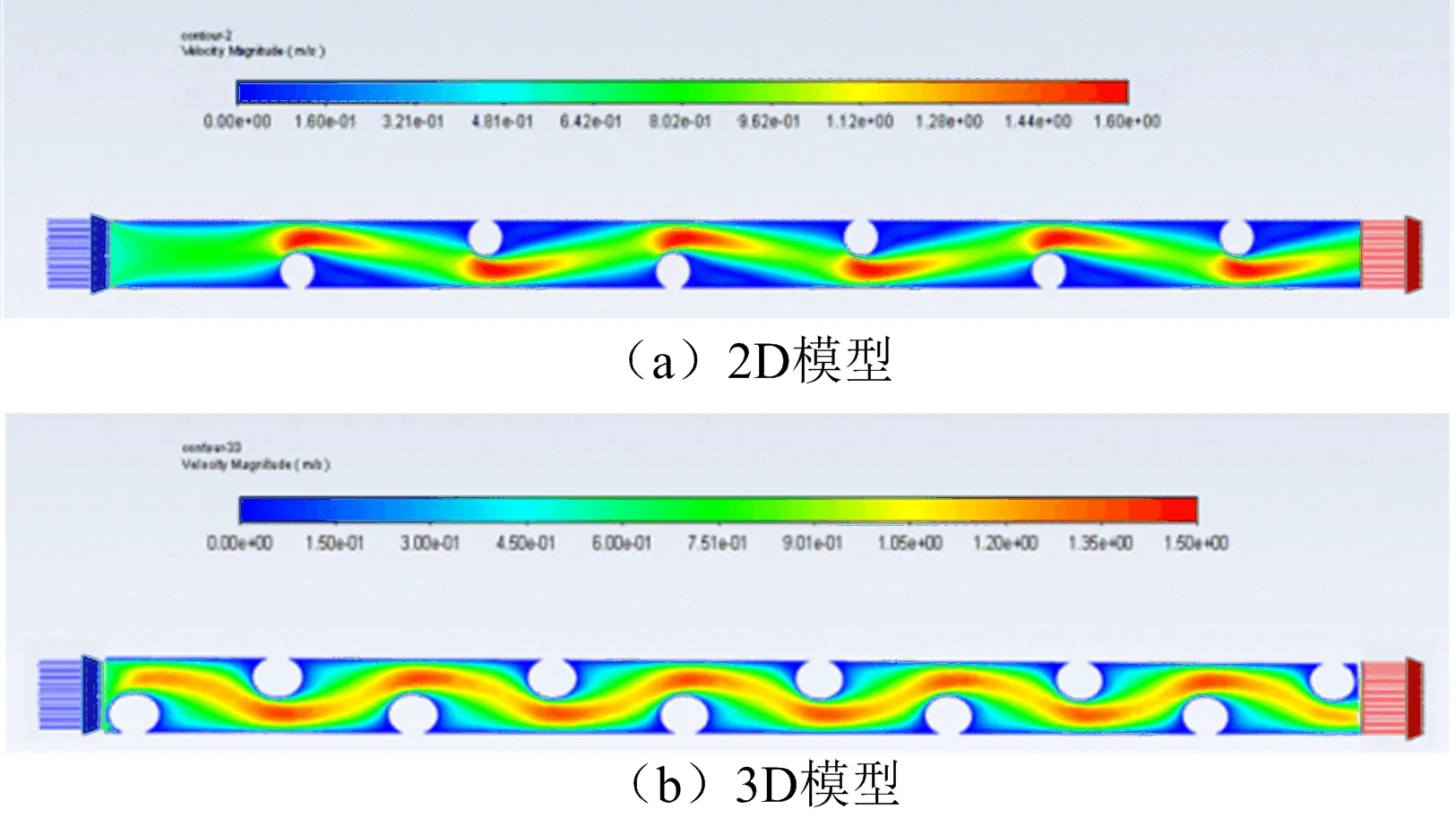
(a)2D模型;(b)3D模型图14 速度云图的比较

2D与3D的速度随y轴变化如图15所示。两种情况下的速度都先增加后下降,且关于y=0.5 mm平面对称,二者结果基本一致,最大误差为14.63%,说明2D模拟与3D具有一定的相似性。

图15 3D速度与2D速度比较

(2)压降比较

图16为2D与3D压降沿x方向的变化,二者趋势一致,压降总体呈现下降的趋势,即入口处压降最大,出口处压降减小为0Pa。但是,2D时压降呈现阶梯状下降,3D时则呈平滑的线性下降,此处二者有明显差异。因此,对卷式膜组件模拟时,2D模拟虽然计算量小速度快,但不能精确地代替3D模拟,3D模拟则能够更好地反映真实流动与流场特性。

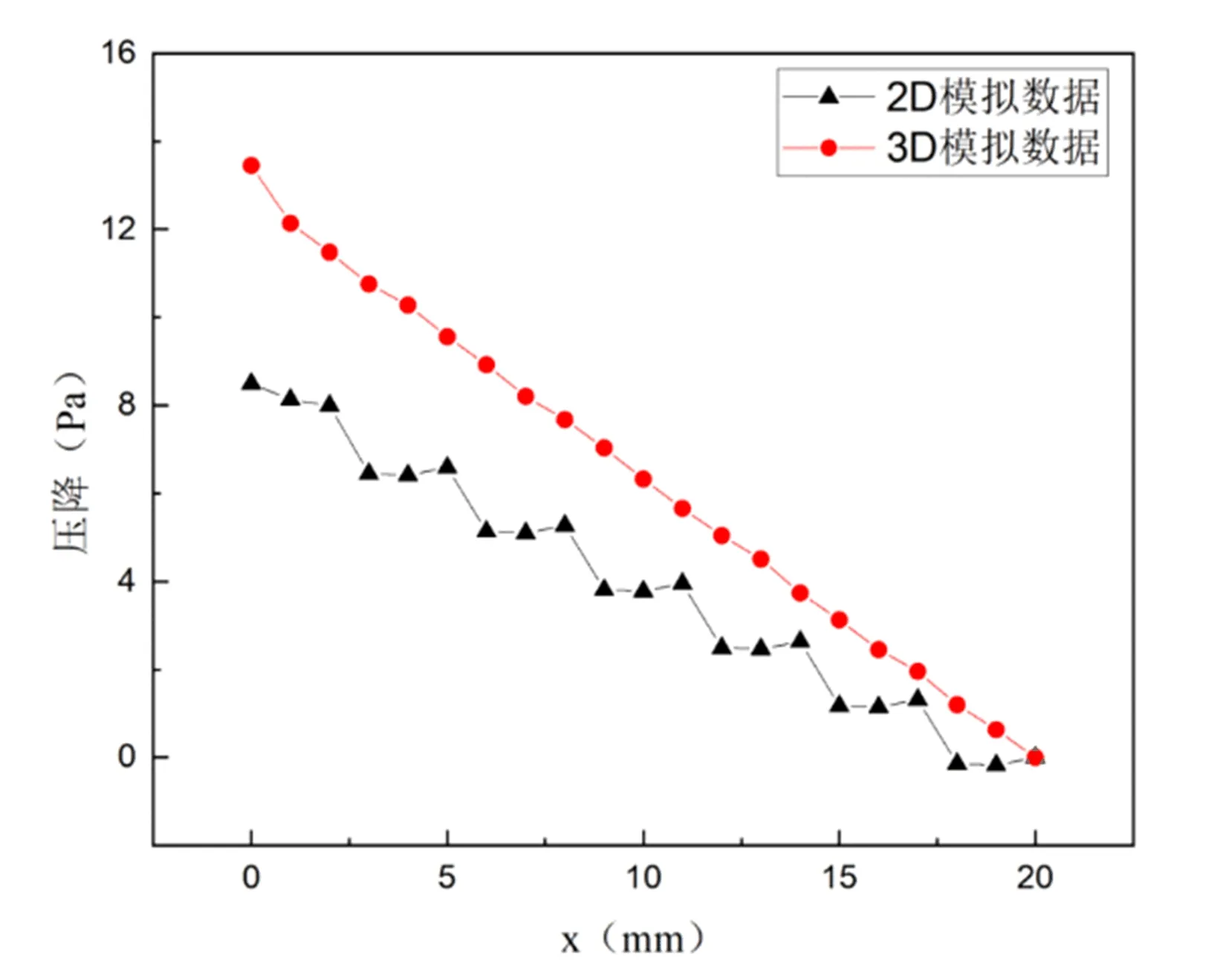
图16 2D与3D压降的比较

3 结论

本文对卷式膜组件的两种入水角进行了计算流体力学模拟,将3D模拟的结果与文献数据和2D模拟结果分别进行比较,探讨入水角度对流体速度、壁面剪切应力和压降的影响,主要得出以下结论:

(1)本文3D模拟结果与文献[4]的速度和壁面剪切应力吻合较好,证明本文方法和结果的可靠性。

(2)0°入水角对流动的阻碍更强,流动速度关于膜组件中心截面对称,增强了靠近壁面的浓差极化,易于诱发膜污染;且下隔网壁面剪切应力较小,膜的利用率较低。与此同时,上、下隔网壁面剪切应力差别较大,降低整体稳定性,也会减少膜材料的寿命。

(3)从减少浓差极化、降低能耗、提高膜面利用率等方面出发,45°入水角都优于0°入水角,因此在工艺设计或操作优化中,应该优先选择入水45°角。

(4)通过压降曲线的对比可知,进行2D模拟不准确,容易遗漏信息;而3D模拟则更精准地反映流场中物理量的分布规律。