基于变参数控制的复合导引头伺服系统设计

胡小波，张 瑞，赵 阳，田永全，孙 琦，魏 鑫

(北方光电股份有限公司，陕西 西安 710043)

0 引言

随着电子技术的快速发展,现代战争中的战场环境日趋复杂,各种干扰技术层出不穷,采用传统单一的制导模式的导引头极容易被干扰影响,导致智能弹药的作战效能下降,而复合制导技术可以有效的克服这一缺点,更好的应对战场环境[1]。存在的问题是,虽然采用了复合制导技术的平台式导引头可以通过使用不同模式的感知系统探测目标的不同特征,从根本上加强了抗干扰能力,但是这样为平台式双模或多模复合导引头的伺服控制系统带来了其他问题。例如文中平台式可见光和红外复合制导导引头在不同的工作模式下,会因探测器分辨率、视场角及光学系统设计指标的不同,导致两种模式输出的跟踪偏差信息存在较大差别,此时继续使用常规的PID控制方法已经不能同时满足可见光和红外复合导引头的控制精度和动态性能。而采用“变参数”PID控制方案可以根据不同的制导模式,实时变换控制参数,从而更好地适应由于模式切换导致的“位置环”输入偏差变化,进而能够输出稳定的视线角速度信息,满足整弹应用要求。

1 导引头伺服系统建模

1.1 伺服系统工作原理

文中导引头伺服控制系统由“电流环”、“速度环”和“位置环”构成,伺服系统原理框图如图1所示[2]。

图1 导引头伺服系统原理框图Fig.1 Seeker servo system schematic block

该伺服控制系统为“三环”控制系统,从内到外依次是电流环、速度环和位置环。各个环路的作用主要有[3]:

1)电流环。电流环的作用是控制电机转矩,任何控制模式都需要电流环,电流环是控制的根本,在系统进行速度和位置控制的同时,系统也在进行电流/转矩的控制以达到对速度和位置的相应控制。电流环减小了元件参数不稳定对系统的影响及控制回路内元件非线性因素的影响[4]。

2)速度环。速度环作为电流环的外环,其输入是期望速度和速度传感器实测的速度差值,如果速度环参数选择合理,与电流环配合良好,就可以形成一个性能较好的稳定平台,使被控载体在惯性空间保持稳定,隔离弹体扰动对导引头伺服系统带来的干扰[5]。

3)位置环。位置环在整个控制系统中处于最外环的位置,主要作用是给伺服控制系统输入所期望到达的运动位置。

整个导引头伺服系统的工作流程为:导弹在上电后,导引头一般处于电锁状态,利用位置传感器的反馈,使光轴保持在框架零位;在导弹发射后,切换控制回路至“搜索模式”,此时导引头接收来自“搜索回路”的“速度指令”,见图1中的“速率指令”,实时控制光轴的指向,搜索攻击目标,这样做的好处是利用导引头稳定平台使光轴隔离了弹体扰动带来的影响,回传至地面的图像信息稳定、清晰;一旦导引头锁定攻击目标,导引头切换至“跟踪回路”,此时“位置环”的输入为“跟踪偏差信息”,导引头光学系统对目标进行稳定跟踪,并输出视线角速度至弹上计算机,引导导弹命中目标。

文中电视和红外双模导引头主要由共口径光学系统、伺服驱动系统、图像跟踪系统等构成。其中伺服驱动系统包含电机、角度传感器、速度传感器、轴承、配重零件以及导线等,系统较为复杂,准确建立整个系统的模型数学模型十分困难,文中主要对双模导引头跟踪回路的控制方法进行研究和仿真,主要建立导引头的跟踪回路模型。

1.2 跟踪回路建模

导引头的稳定平台可以同时在方位和俯仰两个方向进行运动,因为负载和干扰力矩存在差异,一般情况下这两个回路的控制参数也是不同的,但其控制原理和方法是一致的,因此以导引头框架的“内环”进行仿真和建模。

1.2.1 功率放大电路模型

功率放大电路是控制系统的一个环节,其输出的控制信号随输入的PWM信号占空比变化,因为功率放大电路特性,输入和输出存在一个最大可达一个开关周期的延迟,因此,在建立PWM功放数学模型时,将其作为一阶之后环节进行处理,其传递函数为[6]:

(1)

式中:Ks为功率放大器的放大系数;Ts为延迟时间常数。

考虑到功率放大器的频率为十几kHz,因此可以将滞后环节看做一个一阶比例环节:

综上分析,功率放大电路的数学模型可简化为Ks。

1.2.2 力矩电机模型

力矩电机的电压平衡方程为[6]:

(2)

电磁转矩计算公式为:

Mm=CmIa

(3)

转矩平衡方程为:

(4)

式中:Ce为反电动系数;Cm为电机转矩;La、Ra为电枢电感和电枢电阻;Ia为电枢电流;ω为电机转速;J为电子转子上的总转动惯量。

综上分析,力矩电机和负载的数学模型如图2所示。

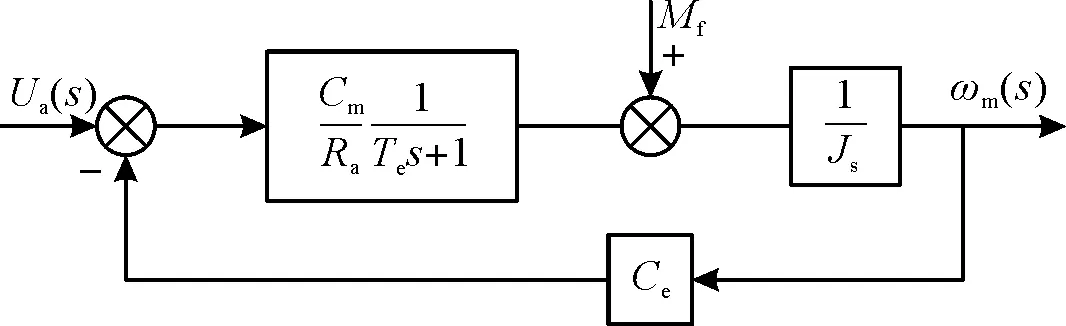
图2 力矩电机模型框图Fig.2 Torque motor model block diagram

1.2.3 陀螺模型

速率陀螺的输出与其敏感的角速度成正比例关系,其数学模型为:

(5)

式中:ζ为阻尼比;ωn为固有角频率;Kt为陀螺输出斜率。

综上分析,可以得到导引头的跟踪回路模型如图3所示。

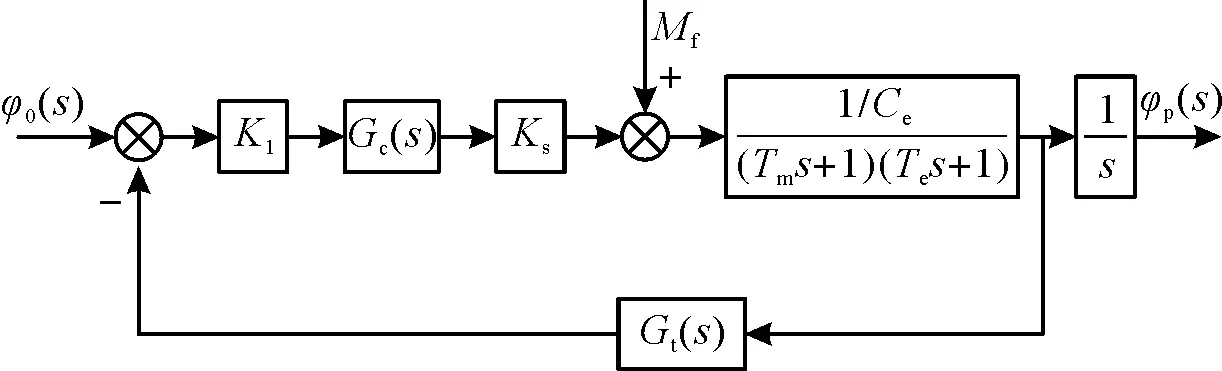
图3 跟踪回路模型图Fig.3 Track loop model diagram

其中:Gc(s)为跟踪回路校正网络传递函数;K1为前相通道增益;Ks为功率放大器比例系数;Gt(s)速率陀螺环节传递函数。

2 跟踪回路控制系统仿真对比

为适应导引头跟踪回路精度高、响应快、超调量小等要求,需要使用一种数字控制系统对“偏差信息”进行实时校正。目前广泛采用的控制方法主要有常规PID控制、基于观测器的PID控制、神经网络PID控制[8]。文中考虑到工程实际应用中,复杂的算法和低功耗、低成本的矛盾,因此仅对常规PID控制方法、变参数PID控制方法在双模导引头跟踪回路中的性能进行对比分析。

2.1 常规PID控制模型

图4为常规PID控制仿真模型。常规PID采用的是电流环、速度环、位置环控制模式,其中位置环为外环,其输出为速度环的输入,而速度环的输出为电流环的输入。

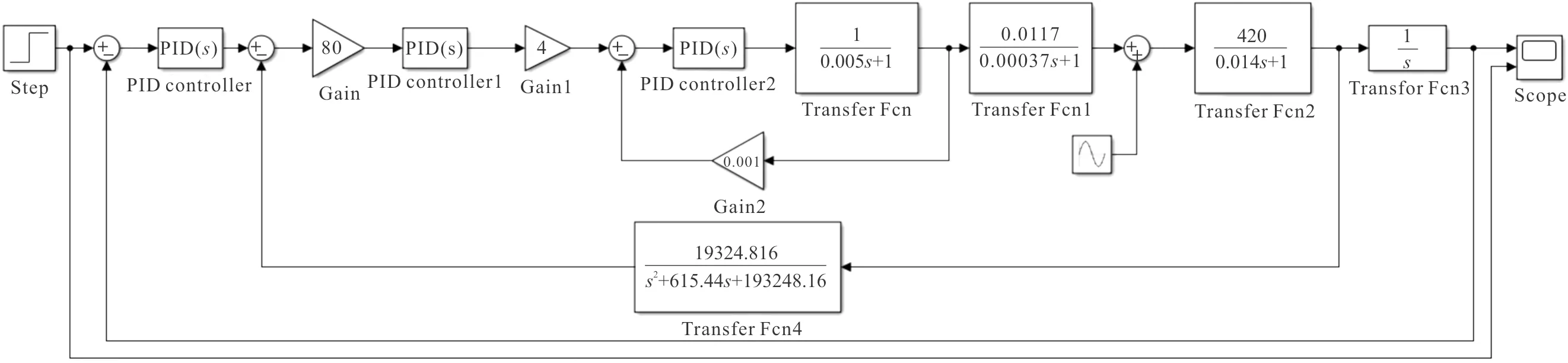
图4 常规PID控制仿真模型Fig.4 Track loop model diagram

2.2 变参数PID控制模型

图5为变参数PID控制仿真模型。文中的变参数控制模型其速度环和电流环与常规PID控制模型是一致的,其变参数主要体现在图5中位置环的自适应参数变化环节。该环节的主要作用是将位置环的PID参数误差和误差的变化量相关联,在工程应用中,一般需要设置PID参数的基础值及变参数的可调节范围,其实质是一种自适应PID控制参数调节方法[7]。

图5 变参数PID控制仿真模型Fig.5 Variable parameter PID control simulation model

2.3 对比分析

图6、图7为常规PID控制和变参数PID控制在阶跃输入下的响应曲线。

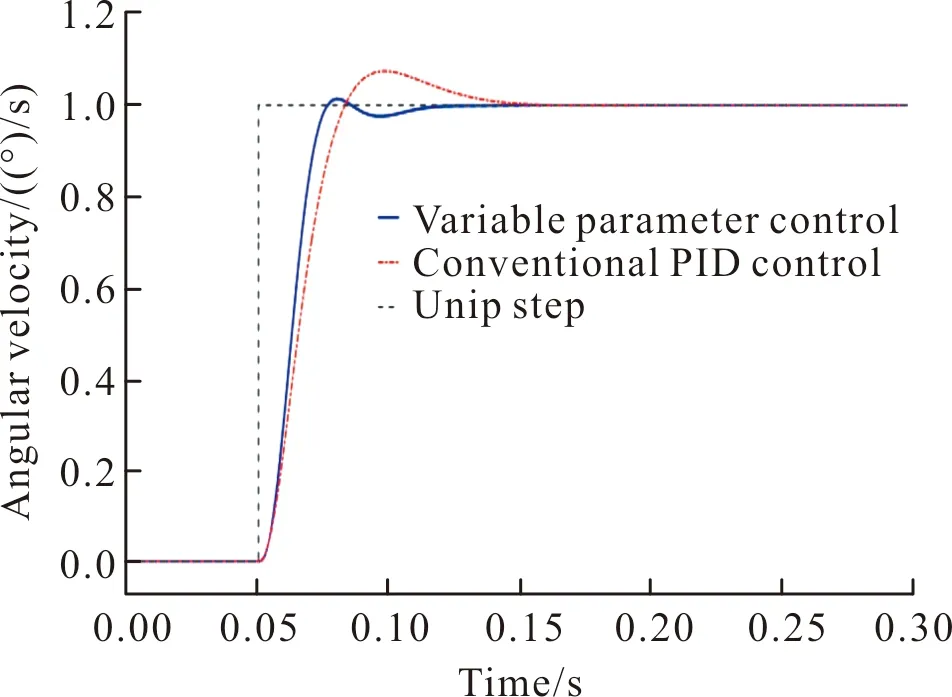
图6 1°阶跃响应Fig.6 Step response of 1°

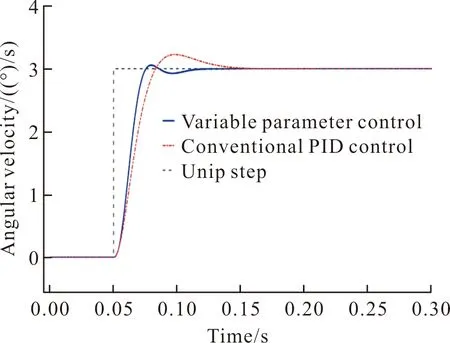
图7 3°阶跃响应Fig.7 Step response of 3°

图6所示为1°阶跃响应,图7为3°阶跃响应,由仿真结果可以明显的看出,在两种不同的阶跃激励输入下,变参数PID控制较常规PID控制在上升时间、超调量、稳态时间等指标上均具有明显优势,其中上升时间由原来的100 ms缩短至50 ms;超调量由8%下降至3%;稳态时间由150 ms缩短至60 ms。

作者团队在进行可见光和红外复合制导导引头控制系统的设计、测试过程中,发现了控制回路的位置环输入在同样的阶跃条件下,可见光模式和红外模式各自输出的跟踪偏差信息存在较大差异,而跟踪偏差信息是制导控制规律的重要信息,如果使用常规PID控制,在工程实际应用中可能会出现使用双模制导导引头的可见光模式或红外模式对同一运动目标进行跟踪时,伺服系统会顾此失彼,无法同时满足双模复合制导导引头的技术指标要求,具体表现为两种模式的伺服系统性能不一致。而变参数PID控制方法的控制参数会根据不同的输入实时调整控制参数,可以很好的解决常规PID控制方法在双模制导系统中的出现问题。

3 结论

为了解决可见光和红外复合制导导引头在不同的工作模式下,因探测器分辨率、视场角及光学设计指标的不同,导致两种模式输出的跟踪偏差信息存在较大差别,使用常规PID无法同时满足两种模式的跟踪计数指标要求,文中提出了变参数复合导引头PID控制方案,建立了两种控制方法的跟踪回路控制模型,进行仿真验证和分析。结果表明:采用变参数复合导引头PID控制方案能提升复合导引头动态性能,减小跟踪误差。