PID 控制器参数的优化整定方法

刘 宁 柴天佑

比例-积分-微分(Proportional-integral-derivative,PID)控制技术因其结构简单,使用方便而广泛应用于实际工业过程,目前约95%的控制回路采用PID 控制技术[1-3].PID 控制器的性能取决于比例、积分和微分三个参数.文献[4]指出: “··· 没有一种整定方法可以说是通用的或最优的,迄今为止,我们仍缺乏足够的知识来确定一个通用且最优的PID 控制器参数的整定方法.”因此PID 控制器参数整定方法一直是控制领域研究的重要方向.

目前工业领域广泛采用的PID 控制器参数整定技术是Ziegler-Nichols (Z-N)法[5].Z-N 法采用可以反映被控对象动态特性的临界点,即其Nyquist曲线穿越负实轴的 -180°相位点的增益K180和频率ω180来设计PID 控制器参数.Z-N 法使闭环系统对阶跃负载扰动的响应以1/4 的震荡比衰减,得到基于临界点增益和频率的简单的PID 参数整定规则.Z-N 法将PID 控制系统的开环传递函数在ω180点的频率响应调节为 -0.6-0.28j,在保证控制系统稳定的条件下,获得好的抗扰性.Z-N 法仅适用于时间常数较大的慢动态工业过程[6-7].文献[8-9]以给定的PID 控制系统开环传递函数在ω180点的频率响应的幅值和相角为目标,从而提出了基于临界点增益和频率的PID 控制器参数整定规则.文献[10-11] 采用被控对象在临界点的频率和增益建立积分滞后模型,文献[12] 采用被控对象的稳态增益与 -180°相位点的增益和频率建立一阶惯性滞后或二阶欠阻尼滞后模型,文献[13]采用被控对象的稳态增益、-180°相位点的增益和频率及该点Nyquist曲线的切角建立二阶滞后模型,以期望的控制系统传递函数为目标,提出了基于临界点增益和频率的PID 控制器参数整定方法.为提高PID 控制系统的性能和鲁棒稳定性,文献[14] 针对基于临界点频率和增益的被控对象模型,以PID 控制器的积分增益最大为优化指标,以敏感度为约束,提出了基于临界点频率和增益的PID 控制器参数整定规则.但积分增益最大的优化指标只适用于平稳的被控对象,当负载扰动频繁波动时,不能减小跟踪误差[9].

上述PID 参数整定方法要求被控对象必须存在临界点.然而低阶或相对阶次较小、延时很小的被控对象不存在临界点.文献[15-16]采用反映其动态特性的 -120°相位点的增益K120和频率ω120,以给定的PID 控制系统开环传递函数在ω120点的频率响应的幅值和相角为目标,提出了PID 参数整定规则.针对离散被控对象,文献[17-18]提出离散的Z-N 法.文献[19]以给定的PID 控制系统开环传递函数在ω180点的频率响应的幅值与相角为目标,提出基于临界点的频率和增益的离散PID 控制器参数整定方法.

上述PID 控制器参数整定方法的 -180°或-120°相位点的增益和频率参数采用实验方法近似求取.当被控对象模型已知时,文献[18,20] 提出临界点增益和频率的数学计算方法.文献[18] 引入比例控制与被控对象组成闭环回路,通过临界稳定条件下闭环特征方程的根计算使闭环系统临界稳定的比例增益和对应的频率,得到临界点的增益K180和频率ω180.该方法只适合低阶的被控对象.文献[20]建立被控对象的相位等于 -180°的方程,采用Newton-Raphson 算法迭代求解该方程,计算临界点的增益K180和频率ω180.迭代算法时间长且存在计算误差,相位点增益和频率的求取误差影响PID 控制系统的性能.

本文通过引入Tchebyshev 多项式和分数阶积分器,提出被控对象 -180°和 -120°相位点的频率和增益的求取方法.为了获得基于相位点频率与增益的PID 参数优化整定规则,本文基于被控对象指定相位点频率和增益的积分滞后模型,以负载扰动下跟踪误差的平方和(sum of squares of tracking errors,SSE)最小为优化目标,以最大灵敏度和最大补灵敏度为约束,提出实现上述优化性能指标的基于被控对象相位点频率和增益的PID 控制器参数整定规则.采用存在临界点和不存在临界点的被控对象的仿真和物理实验,表明所提方法的优越性.

1 被控对象模型

本文的被控对象为[18,20]:

其中,u(k)为被控对象的输入,y(k)为被控对象的输出,d为系统延时,k=t/T0=0,1,2,··· 为离散的采样时间,T0为采样周期,A(z-1)和B(z-1)为关于z-1的多项式,即为:

其中,n表示系统阶次.以上被控对象的传递函数为:

本文考虑的被控对象包括两类: 一类是频率响应经过 -180°相位线(负实轴)的被控对象,称为A 类被控对象,这类被控对象存在临界点,包括大多数存在延时的工业被控对象;一类是频率响应不经过 -180°相位线但经过 -120°相位线的被控对象,称为B 类被控对象,这类被控对象不存在临界点.B 类被控对象主要包括稳定的二阶最小相位系统和很多相对阶次小于3 的系统[15].

对于A 类被控对象,采用其 -180°相位点的数字频率θ180和增益K180表征被控对象的动态特性,该点被称为临界点[14];对于B 类被控对象,采用其-120°相位点的数字频率θ120和增益K120描述被控对象的动态特性[15-16].为统一描述两类被控对象在指定相位点的频率和增益的求取方法及PID 控制器参数的优化,定义θφ和Kφ表示被控对象在指定相位点的频率和增益:

若GP(z)为A 类被控对象,θφ和Kφ表示其-180°相位点的频率和增益,即

若GP(z)为B 类被控对象,θφ和Kφ表示其-120°相位点的频率和增益,即

1.1 -180° 和 -120° 相位点的频率和增益的求取方法

本文引入Tchebyshev 多项式[21]和分数阶积分器[22]提出两类被控对象的 -180°和 -120°相位点的数字频率和增益的求取方法如下.引入分数阶积分器F(z),串联B 类被控对象传递函数(4)使其频率响应穿越 -180°相位.对于A 类被控对象,F(z)=1.这样可采用统一的方法求取两类对象的频率θφ和增益Kφ.引入Tchebyshev 多项式,将被控对象传递函数关于超越函数 ejθ的高次幂的复杂的相位方程转化为关于实变量u的方程,通过求解该方程即可得到被控对象传递函数的 -180°和 -120°相位点的数字频率和增益.

定义传递函数:

若GP(z)为A 类被控对象,令F(z)=1 ;若GP(z)为B 类被控对象,令F(z)为如下的分数阶积分器:

由文献[15,23]知,以上分数阶积分器的相角始终为 -60°,即:

由于分数阶积分器(9)无法直接求解,采用连分式展开(Continued fraction expansion,CFE)技术[22]将其近似为整数阶系统计算频率响应:

其中,CFE{x}表示对x的连续分式展开,P(z)和Π(z)为关于z的多项式,m表示近似的阶次,本文令m=5,由文献[22]知P(z)和 Π (z)为:

其中,

其中,

采用近似分数阶积分器(11),H(z)可写为:

通过引入F(z),对两类被控对象,构造的传递函数H(z)必与负实轴相交.

令

则单位圆上z可以写为[21]:

随着θ从0 到π,u在-1 到1 之间运动.

由于

定义:

由文献[21,24]知,cκ和sκ为关于u的第一类和第二类Tchebyshev 多项式.则zκ等于

采用如下的递推公式可求得cκ(u)和sκ(u):

将式(19)代入式(14)可得β(u)和χ(u):

式中,Rβ(u),Tβ(u),Rχ(u),Tχ(u)分别为

H(z)可以写为:

由于所求Kφ和θφ为H(z)的Nyquist 曲线与负实轴相交的第一个交点的增益和频率,定义

则Kφ和uφ满足如下的方程:

由式(29)知

或者

由于u的取值范围为 [-1,1],且u=±1 对应于θ=0 和θ=π,而θφ且θφπ,因此uφ满足

由式(20)和(23)～(26)知,由于传递函数GP(z)和系数可知,式(35)和(36)所有系数已知.在H(z)的Nyquist 曲线上,可能存在多个虚部为0 的点,而θφ为其中使 Re(H)＜0 的最小频率.由式(15)知,u为关于θ的单调递增函数,因此uφ为(-1,1)区间内使式(36)小于0 的式(35)的最小解.

由式(30)可得

将uφ代入式(28)可得 R e(H(uφ)),当被控对象为A 类,由式(31)得

其中,

由式(31)得

其中,

1.2 基于指定相位点频率和增益的被控对象模型

由1.1 节得到的两类被控对象在 -180°相位点或 -120°相位点的频率和增益建立积分滞后模型.为方便PID 控制器参数优化指标的设计,将两类被控对象的离散积分滞后模型统一描述为[11,25-26]:

其中,Kφ和θφ由式(5)～(7)给出,分别为 -180°或-120°相位点的增益和频率.η决定了两类被控对象的积分滞后模型的延时项的相位滞后,若GP为A类被控对象,η=2 ;若GP为B 类被控对象,η=6.

对于积分滞后模型(43),若GP(z)为A 类被控对象,在θ180点,有

即积分滞后模型(43)与被控对象的传递函数(4)在θ180点的频率响应一致.同理,若GP(z)为B 类被控对象,在θ120点,有

此时积分滞后模型(43)与被控对象的传递函数(4)在θ120点的频率响应一致.

采用基于指定相位点频率和增益的积分滞后模型(43)的目的是设计优化的PID 控制器参数,式(43)不需要物理实现,因此该模型不需要必须为有理真分式.

2 PID 控制器参数的优化整定方法

2.1 PID 控制器参数的优化整定策略

采用被控对象的积分滞后模型(43),以负载扰动下跟踪误差的平方和最小作为优化指标,闭环系统的最大灵敏度在1.2 到2 之间[14,27],最大补灵敏度在1 到1.5 之间[14,27],及PID 控制器的微分时间常数TD等于积分时间常数TI的四分之一[28]作为约束方程,求取基于被控对象指定相位点频率和增益的PID 控制器参数整定规则.

首先利用负载扰动的低频特性,跟踪误差对负载扰动的响应主要取决于PID 控制器[27],得到负载扰动下跟踪误差平方和的近似表达式.

为了使PID 控制器参数的选择与被控对象指定相位点的频率θφ和增益Kφ相联系,引入参数ρK和ρT使KP=ρK/Kφ,TI=2πρT T0/θφ.采用序列二次规划算法求解实现上述优化指标的基于θφ的ρK和ρT,从而建立基于被控对象指定相位点频率和增益的PID 控制器参数优化的整定规则.

2.2 PID 参数整定的优化性能指标

PID 控制器为:

其中,KP为PID 控制器的比例增益,TI和TD为积分时间常数和微分时间常数,T0为采样周期.上述PID 控制器的传递函数为:

在负载扰动υ(k)下,被控对象模型(43)在PID控制下的闭环控制系统如图1 所示.其中ysp(k)为设定值,u(k)为被控对象输入,y(k)为被控过程输出,e(k)为跟踪误差,e(k)=ysp(k)-y(k).

图1 闭环控制系统结构Fig.1 Structure of closed-loop control system

定义eυ(k)为扰动信号υ(k)下的跟踪误差,即ysp(k)=0 时,跟踪误差e(k)对扰动信号υ(k)的响应.扰动υ(k)到跟踪误差e(k)的传递函数为

由于PID 控制器包含积分,因此上式中,

由于负载扰动υ(k)通常是低频的[27],由式(48)和(49)知,跟踪误差e(k)对负载扰动υ(k)的响应主要取决PID 控制器.因此扰动υ(k)到跟踪误差e(k)的传递函数可近似表示为[27]:

在采用指定相位点频率和增益的PID 控制器参数整定方法[5,8-12,14-18]中,PID 控制器参数KP、TI和TD可写为关于指定相位点增益Kφ的倒数和周期Tφ(Tφ=2πT0/θφ)的线性表达式.因此本文为了使PID 控制器参数的选择与被控对象在指定相位点的频率θφ和增益Kφ相联系,引入无量纲参数ρK和ρT,并利用约束方程TD=TI/4,将PID 控制器参数表示为:

将其代入式(50),得:

由文献[29]知当扰动υ(k)为单位阶跃信号,则eυ(k)为:

其中Z-1为z逆变换.则闭环系统在单位阶跃扰动下的跟踪误差的平方和为:

上式中,Kφ只决定SSEυ指标的值,不影响ρK和ρT的优化解,因此选择优化指标为:

以ρK和ρT为决策变量,式(58)为优化指标的PID 参数整定的优化模型为:

式中Ms和Mt分别为闭环系统的最大灵敏度和最大补灵敏度,由文献[14]知Ms和Mt分别为:

2.3 优化PID 控制器参数的整定规则

由于式(58)和(65)中所采用的被控对象的数字频率θφ的取值范围为 (0,π),为了求出使J1最小的ρK和ρT,将θφ按间隔0.02 网格化,对每个网格点,使用序列二次规划(Sequential quadratic programming,SQP)算法[30]求性能指标(59)最小的最优解,图2 和图3 分别表示A 类被控对象与B类被控对象ρK和ρT的最优解曲线.采用θφ和相应的ρK与ρT的最优解数据建立以θφ为输入,相应的ρK和ρT的最优解为输出的多项式.采用基于AIC(Akaike's information criterion)准则的多项式阶次确定方法[31]和最小二乘参数设计方法[32],得A 类被控对象和B 类被控对象使性能指标(59)最小的ρK和ρT如式(66)～(69)所示.

图2 A 类被控对象 ρK 和 ρT 的最优解曲线Fig.2 Optimal solution curve of ρK and ρT of class A controlled object

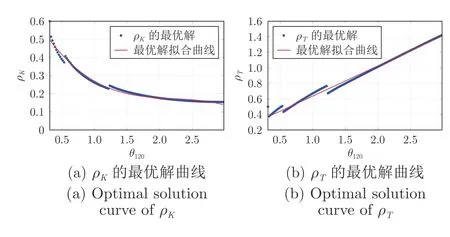
图3 B 类被控对象 ρK 和 ρT 的最优解曲线Fig.3 Optimal solution curve of ρK and ρT of class B controlled object

A 类被控对象:

B 类被控对象:

由式(51)～(53)知,PID 控制器参数的整定规则为:

A 类被控对象Kφ=K180,θφ=θ180;B 类被控对象Kφ=K120,θφ=θ120.

PID 控制器参数整定算法如下:

1)采用第1.1 节的相位点频率θφ和增益Kφ的求取方法,针对A 类对象求得θ180和K180,针对B类对象求得θ120和K120.

2)针对A 类对象由式(66)和(67)求ρK和ρT,针对B 类对象由式(68)和(69)求ρK和ρT,由式(70)～(72)求取PID 控制器参数KP、TI和TD.

注 1.由文献[33]的定理3.5 可知,若实际的被控对象传递函数(4)在单位圆外没有极点,且PID控制器设计模型(43)和实际的被控对象传递函数(4)的频率响应满足

则采用优化指标(59)～(62)所提出的PID 控制器参数整定方法(66)～(72)所设计的PID 控制器可以使实际的被控对象闭环稳定.

注 2.上述PID 参数优化整定规则(式(66)～(72))的关键是求取被控对象的相位点参数Kφ和θφ.本文给出了被控对象模型已知时的计算方法,对于难以建立数学模型的被控对象,可采用阶跃实验法获得[5].

3 仿真实验

采用PID 控制器参数的离散Z-N 法[18]、不存在临界点的被控对象的PID 整定方法[15]、Astrom 的PID 参数优化方法[14]及抗干扰PID 整定方法[7]与本文的PID 优化整定方法进行仿真对比实验.

例 1.采用文献[18]的仿真模型:

系统采样周期为T0=2 s.设定值ysp(t)为:

其中,δ=0,1,T为方波信号的周期,设T=800 s.负载扰动υ(t)为:

采用文献[18]的方法求得被控对象(74)的-180°相位点的增益K180和周期T180(T180=2πT0/θ180)为0.0596 和11.6027 (对应θ180=1.0827),PID 控制器参数KP、TI和TD为:

采用本文方法求得被控对象(74)的 -180°相位点的增益K180和数字频率θ180为0.0596 和1.0827,ρK和ρT为0.1698 和1.1320,PID 控制器参数KP、TI和TD为:

采用文献[18]方法与本文方法的设定值ysp(t)、被控对象输出y(t)及输入u(t)的曲线分别如图4 和图5 所示.采用下列误差绝对值累积和(Sum of absolute error,SAE)[34]和均方误差(Mean-square error,MSE)[35]对两种方法的评价结果如表1 所示.其中N=800.

表1 本文方法与Z-N 法下误差 e (t)的性能评价Table 1 Performance evaluation of error e (t)with the proposed method and Z-N method

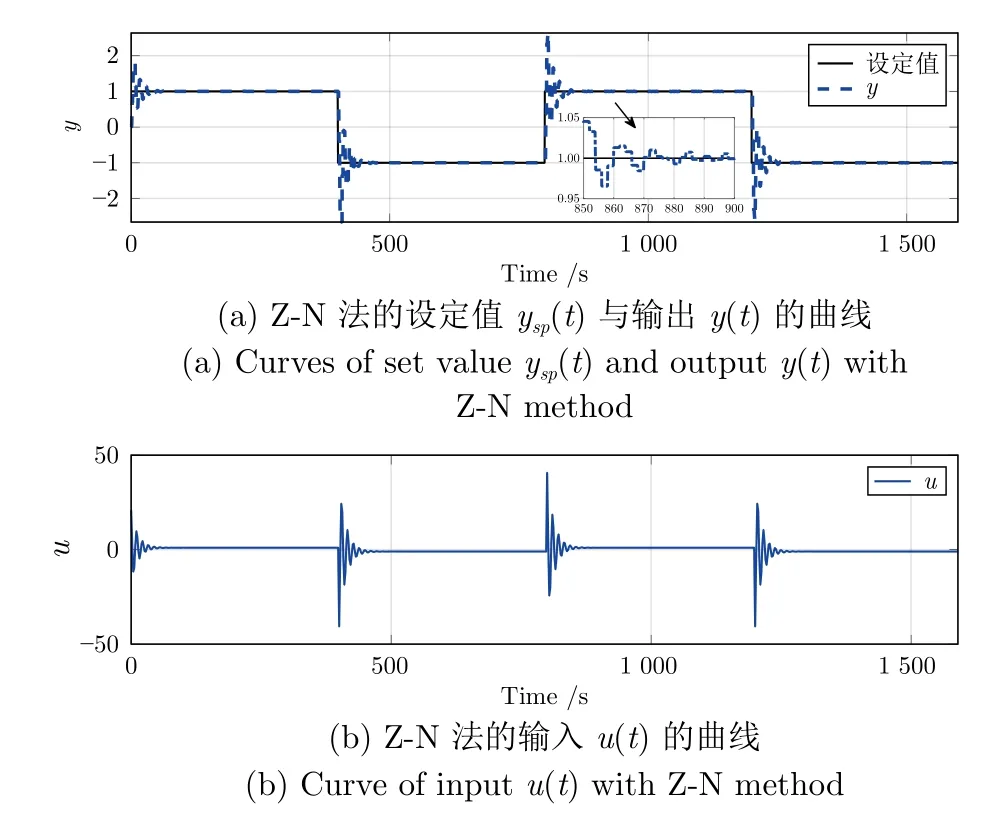
图4 Z-N 法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.4 Curves of set value ysp(t),output y (t)and input u (t)with Z-N method

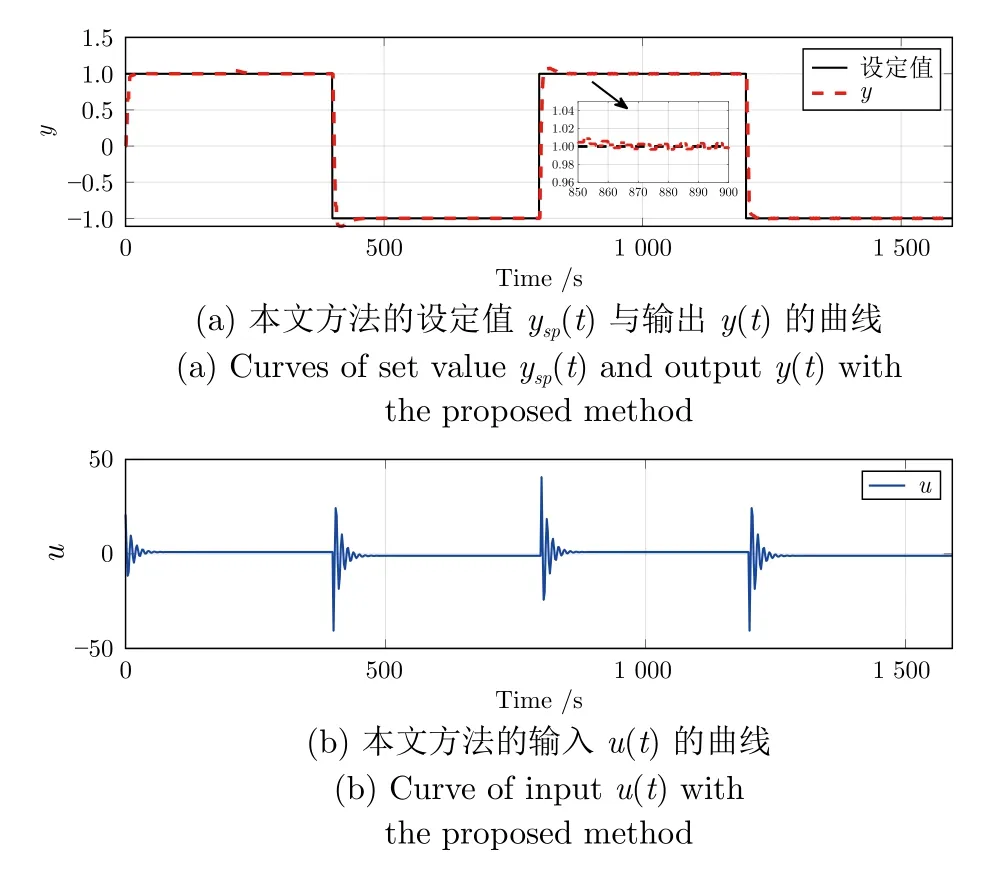
图5 本文方法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.5 Curves of set value ysp(t),output y (t)and input u (t)with the proposed method

由图4、5 和表1 可以看出,虽然采用本文方法求取的模型(74)的 -180°相位点增益和周期与文献[18] 方法相同,但控制效果明显优于Z-N 法,SAE 和MSE 分别降低了52.09%和42.80%.这是因为Z-N 法下闭环系统具有过大的最大灵敏度Ms和最大补灵敏度Mt,分别为4.81 和4.36,远超出Ms和Mt的理想范围[14,27].本文方法的Ms和Mt为1.42 和1.00,因此在设定值和扰动频繁变化下本文方法使闭环系统保持好的动态性能.

例 2.采用文献[15]的B 类被控对象的仿真模型:

图6 为以上被控对象的Nyquist 曲线,可以看到,其Nyquist 曲线不穿越负实轴.设定值ysp(t)为:

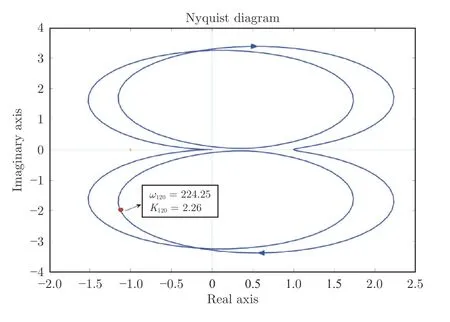
图6 被控对象(81)的Nyquist 曲线(K120=2.26,ω120=224.25)Fig.6 Nyquist curve of controlled plant (81)(K120=2.26,ω120=224.25)

设δ=0,1,T=10 s.负载扰动υ(t)为:

采用文献[15] 的方法求得被控对象(81)的-120°相位点的增益K120和频率ω120为2.3581 和232,PID 控制器参数KP、TI和TD为:

设置采样周期T0=0.001 s,将被控对象(81)离散化.采用本文方法求得其 -120°相位点的增益K120和频率ω120为2.2856 和223.9,数字频率θ120(θ120=ω120T0)为0.2239,ρK和ρT为0.5425 和0.3335,PID 控制器参数KP、TI和TD为:

采用文献[15]方法与本文方法的设定值ysp(t)、被控对象输出y(t)及输入u(t)的曲线分别如图7 和图8 所示.采用式(79)的SAE 和式(80)的MSE 对两种方法的评价结果如表2 所示,其中N=20 000.

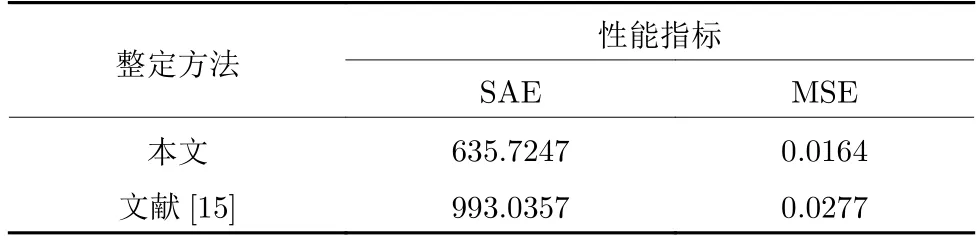
表2 本文方法与文献[15]方法下误差 e (t)的性能评价Table 2 Performance evaluation of error e (t)with the proposed method and the method in reference [15]

图7 文献[15]方法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.7 Curves of set value ysp(t),output y (t)and input u (t)with the method in reference [15]

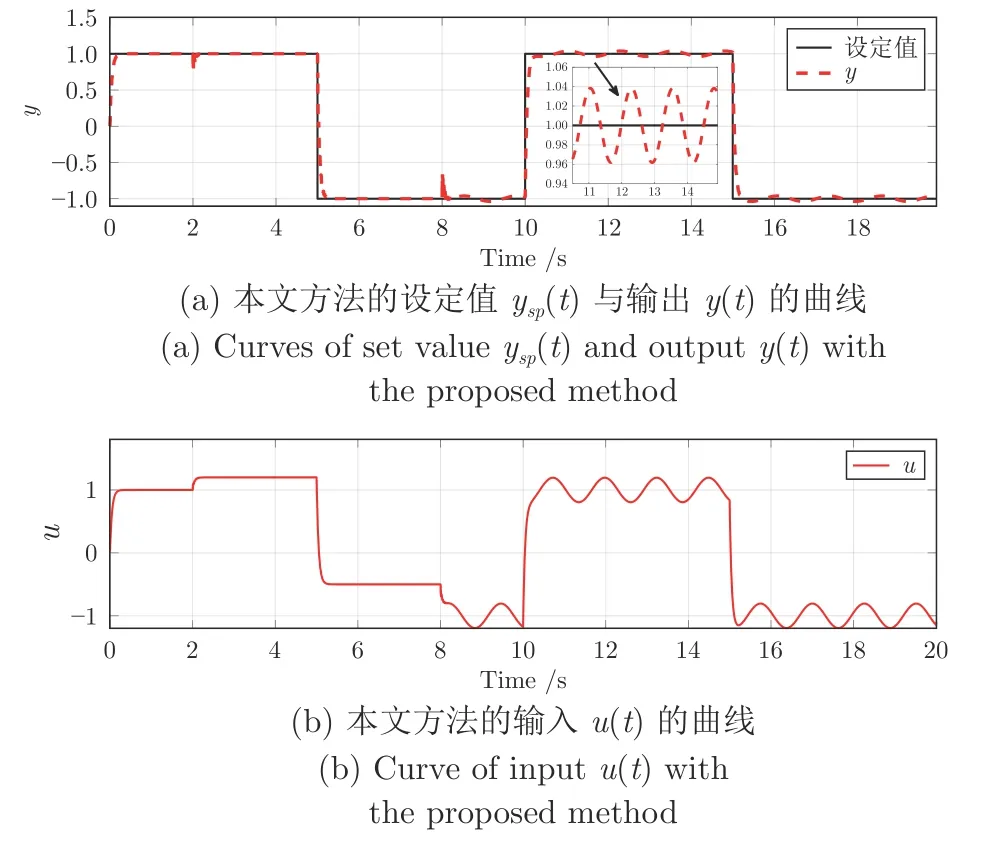
图8 本文方法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.8 Curves of set value ysp(t),output y (t)and input u (t)with the proposed method

由图7、8 和表2 可以看出,本文方法的控制效果优于文献[15]的方法,SAE 和MSE 分别降低了35.98%和40.79%.这是因为文献[15]方法-120°相位点的增益K120和频率ω120是采用继电反馈实验近似求取,与本文方法相比,存在较大的误差.由图6 知被控对象(81)的 -120°相位点的增益K120和频率ω120为K120=2.26,ω120=224.25,文献[15]方法的误差为4.16%和3.34%,本文方法的误差为1.12% 和0.16%.此外文献[15]基于给定的PID 控制系统开环传递函数的相角裕度的整定方法无法有效保证闭环系统的抗扰性[36].本文通过使负载扰动下跟踪误差平方和最小,使得闭环系统具有强的抗扰能力.

例 3.采用文献[14]的仿真模型:

设定值ysp(t)为

设δ=0,1,T=10 s.负载扰动υ(t)为:

采用文献[14]的方法得到被控对象(86)的稳态增益K0为1,-180°相位点的增益K180和周期T180为0.0091 和0.199,PID 控制器参数KP、TI和TD为:

其中λ=K180/K0.

设置采样周期T0=0.01 s,将被控对象(86)离散化.采用本文方法求得其 -180°相位点的增益K180和周期T180为0.0135 和0.2003,数字频率θ180(θ180=2πT0/T180)为0.3136,ρK和ρT为0.2989和0.7861,PID 控制器参数KP、TI和TD为

采用文献[14]方法与本文方法的设定值ysp(t)、被控对象输出y(t)及输入u(t)的曲线分别如图9 和图10 所示.采用式(79)的SAE 和式(80)的MSE 对两种方法的评价结果如表3 所示,其中N=2 000.

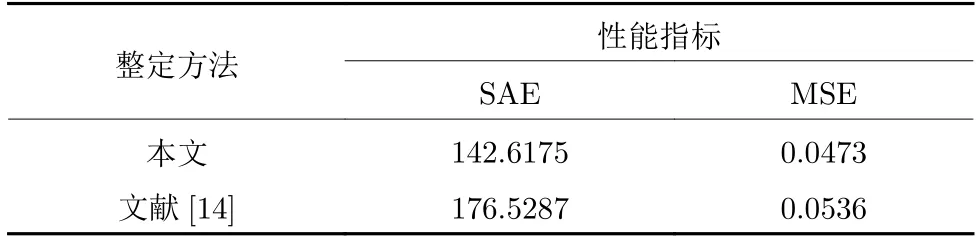
表3 本文方法与文献[14]方法下误差 e (t)的性能评价Table 3 Performance evaluation of error e (t)with the proposed method and the method in reference [14]

图9 文献[14]方法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.9 Curves of set value ysp(t),output y (t)and input u (t)with the method in reference [14]

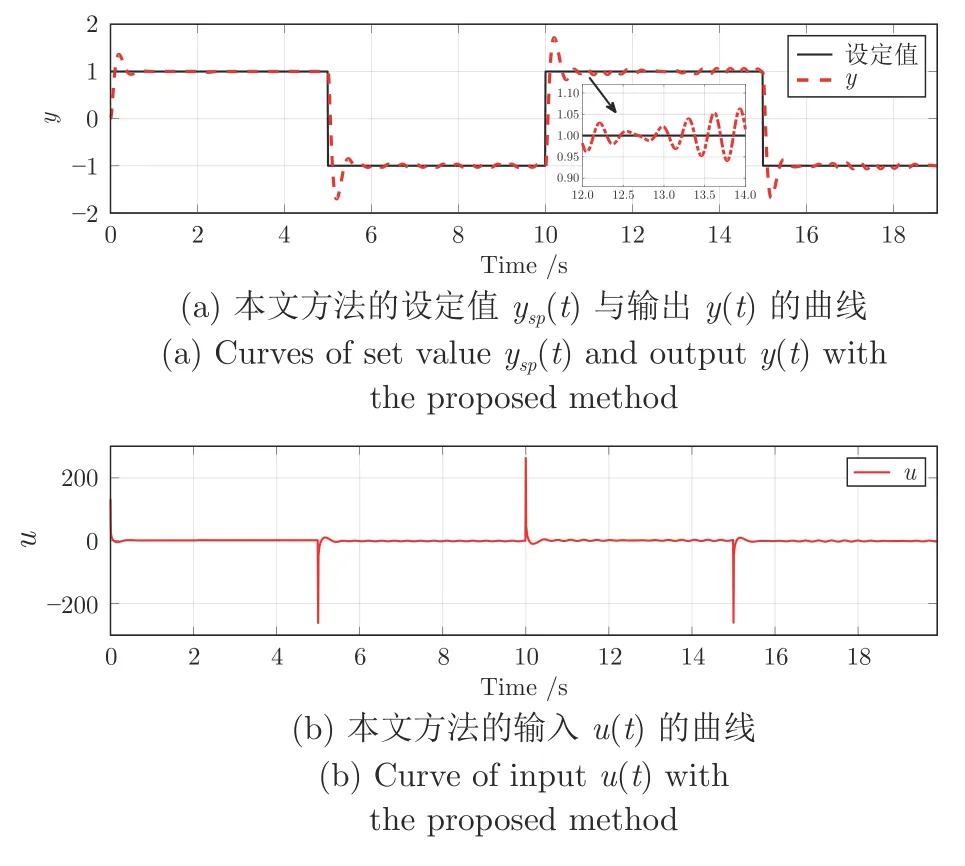
图10 本文方法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.10 Curves of set value ysp(t),output y(t)and input u (t)with the proposed method

由图9、10 和表3 可以看出,本文方法的控制效果优于文献[14]的方法,SAE 和MSE 分别降低了19.21%和11.75%.这是因为Astrom 的PID 参数优化方法使负载扰动下跟踪误差的积分最小的优化指标只适用于平稳的被控过程,当负载扰动频繁变化,不能降低跟踪误差[9,27].本文的跟踪误差平方和最小的优化指标可以在负载扰动频繁变化时有效降低跟踪误差,使闭环系统具有好的跟踪性能.

例 4.采用文献[7]的仿真模型:

设定值ysp(t)为

设δ=0,1,T=800 s.负载扰动υ(t)为:

采用文献[7]的方法求得a0/b0=1,扰动观测带宽ω0为0.356,控制带宽ωc为0.58,调节参数α为0.5,得到PID 控制器参数KP、TI和TD为:

设置采样周期T0=0.1 s,将被控对象(91)离散化.采用本文方法求得其 -180°相位点的增益K180和数字频率θ180为0.6608 和0.0899,ρK和ρT为0.3622和0.6854,PID 控制器参数KP、TI和TD为:

采用文献[7]方法与本文方法的设定值ysp(t)、被控对象输出y(t)及输入u(t)的曲线分别如图11和图12 所示.采用式(79)的SAE 和式(80)的MSE 对两种方法的评价结果如表4 所示,其中N=16 000.

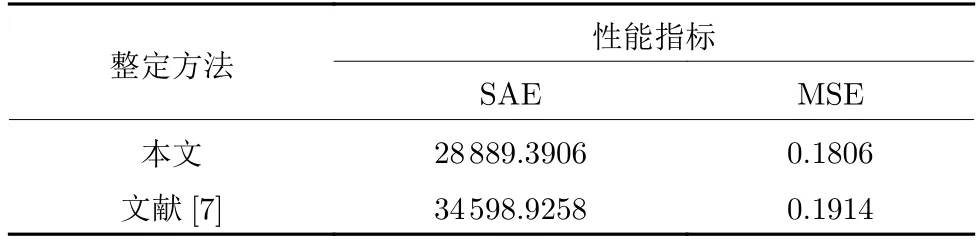
表4 本文方法与文献[7]方法下误差 e (t)的性能评价Table 4 Performance evaluation of error e (t)with the proposed method and the method in reference [7]

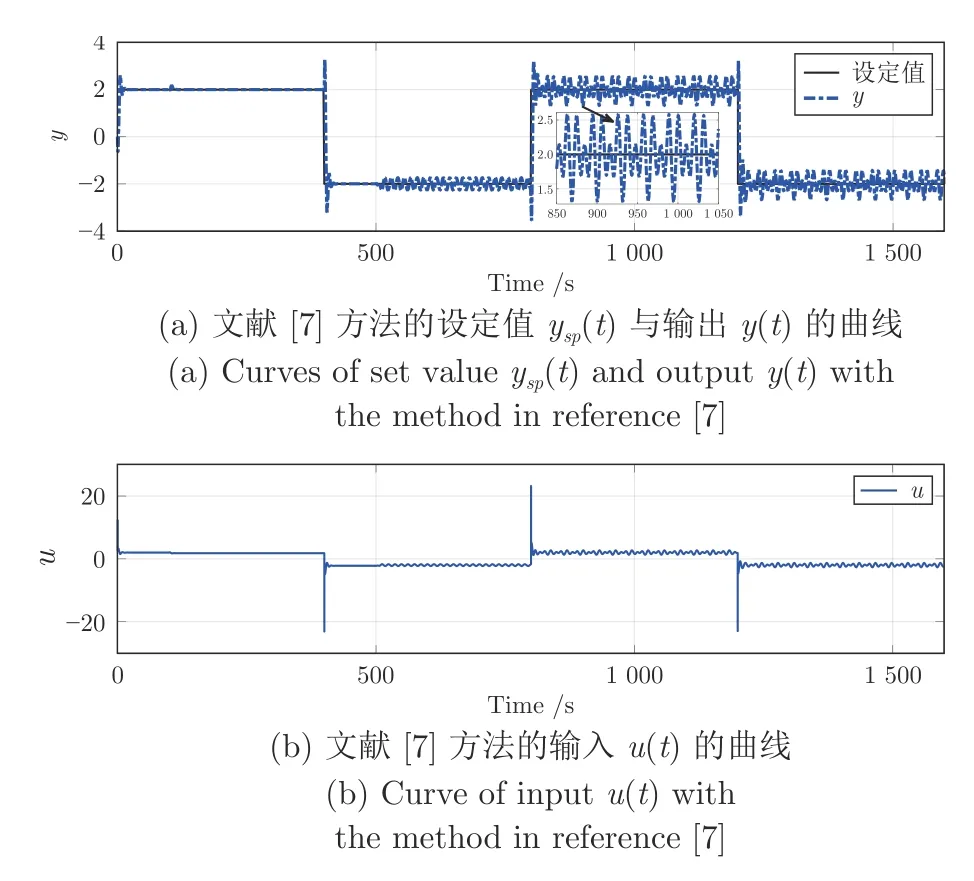
图11 文献[7]方法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.11 Curves of set value ysp(t),output y (t)and input u (t)with the method in reference [7]

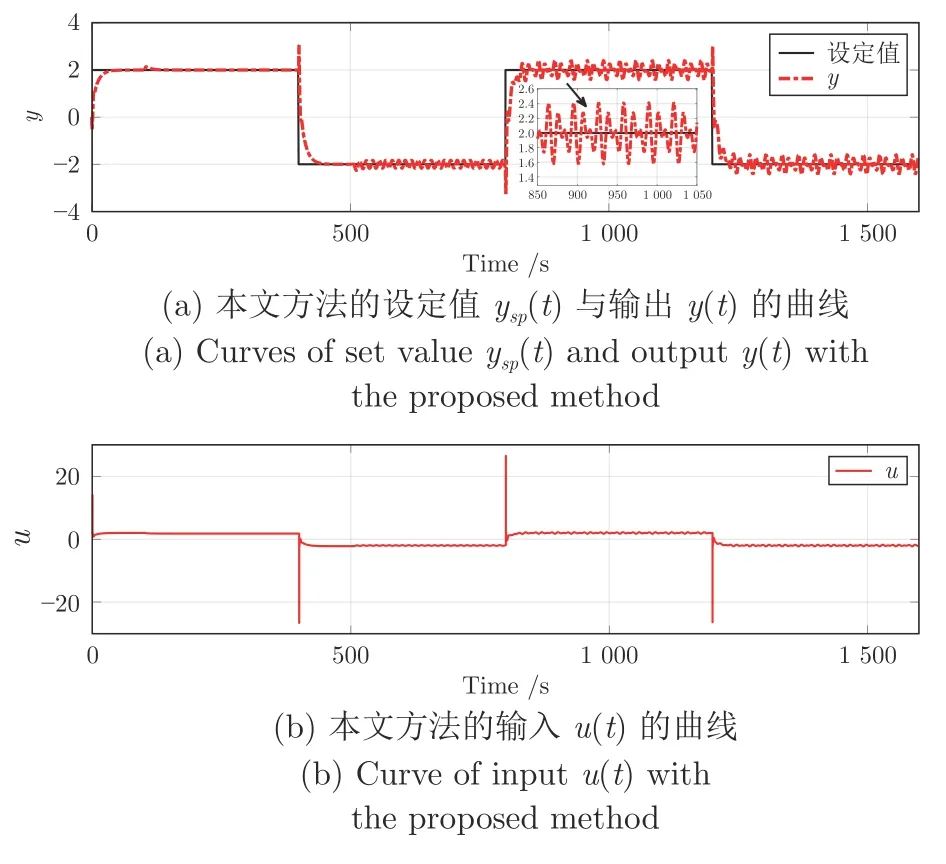
图12 本文方法的设定值 ysp(t)与输出 y (t)及输入 u (t)的曲线Fig.12 Curves of set value ysp(t),output y (t)and input u (t)with the proposed method

由图11、12 和表4 可以看出,本文方法的控制效果优于文献[7]的方法,SAE 和MSE 分别降低了16.50%和5.64%.这是因为文献[7]设计的扰动观测器只能估计平稳变化的扰动.在扰动频繁变化下,扰动观测器的观测误差影响PID 控制器的抗扰性能.

4 物理实验

为验证所提方法的有效性,以空气流量实验系统为对象进行物理实验.实验系统如图13 所示,由空气流量系统,监控计算机,西门子S7-300 PLC 控制系统,检测仪表和执行机构组成.以冷风机频率为控制输入,冷风流量为输出,令采样周期T0=1 s,采集被控对象的输入输出数据,辨识其ARX 模型如下:

图13 空气流量实验系统Fig.13 Air flow test system

设定值为:

设δ=0,1,2,3,T=5 min.

针对实际物理系统,将本文方法与PID 控制器参数的离散Z-N 法[18]及Astrom 的PID 参数优化方法[14]进行比较.采用三种方法的PID 控制器参数如表5 所示.三种方法的设定值ysp(t)、被控对象的输出(冷风流量)y(t)及控制量(冷风机频率)u(t)的曲线如图14～16 所示.可以看到,本文方法下,被控对象的输出对设定值的跟踪性能最好,跟踪精度最高.采用式(79)的SAE 和式(80)的MSE 对三种方法的评价结果如表6 所示,其中N=1 200.本文方法相对于Z-N 法,SAE 和MSE 分别降低76.33%和70.38%,相对于Astrom 方法SAE 和MSE 分别降低18.35%和9.76%,验证了所提方法的优越性.

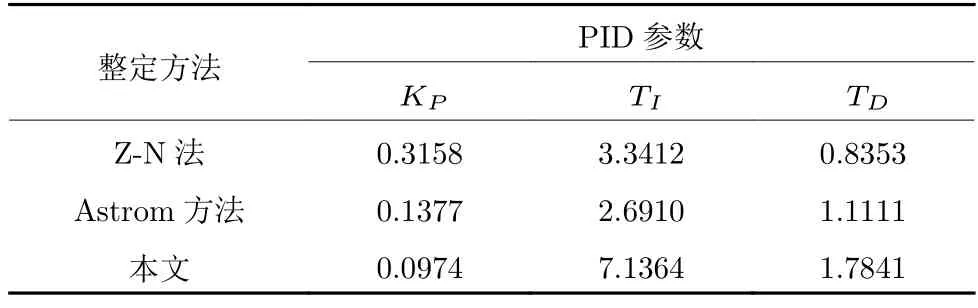
表5 三种整定方法下PID 控制器参数Table 5 PID controller parameters with three tuning methods

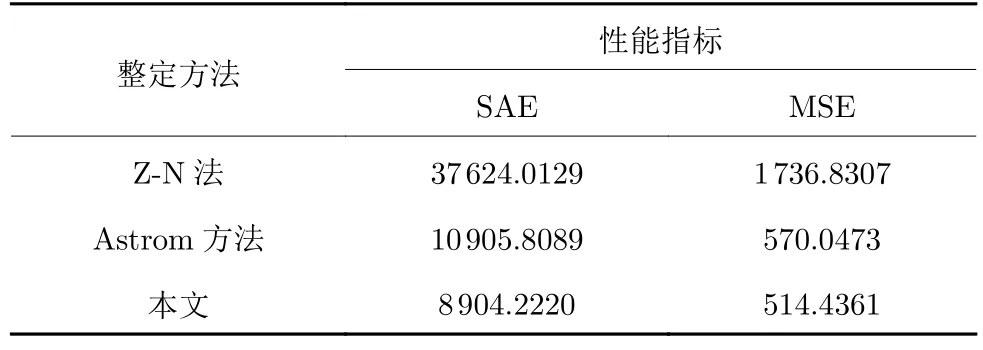
表6 三种方法下误差 e (t)的性能评价Table 6 Performance evaluation of error e(t)with the three methods

图14 Z-N 法的设定值 ysp(t)与冷风流量 y (t)及冷风机频率 u (t)的曲线Fig.14 Curves of set value ysp(t),cold air flow y(t)and air cooler frequency u (t)with Z-N method

图15 Astrom 优化方法的设定值 ysp(t)与冷风流量y(t)及冷风机频率 u (t)的曲线Fig.15 Curves of set value ysp(t),cold air flow y(t)and air cooler frequency u (t)with the optimization method proposed by Astrom

图16 本文方法的设定值 ysp(t)与冷风流量 y (t)及冷风机频率 u (t)的曲线Fig.16 Curves of set value ysp(t),cold air flow y(t)and air cooler frequency u (t)with the proposed method

5 结论

本文针对存在临界点的A 类被控对象和不存在临界点的B 类被控对象,提出了基于 -180°和-120°相位点的数字频率和增益的一种新的PID 控制器参数优化整定方法.该方法包括基于分数阶积分器和Tchebyshev 多项式求取被控对象 -180°或-120°相位点的频率和增益的方法和以阶跃负载扰动下跟踪误差平方和最小为优化指标,以闭环系统的最大灵敏度和最大补灵敏度为约束的PID 控制器参数优化整定规则.仿真和物理实验表明所提PID 控制器参数整定方法的优越性.