计及不确定性的配电网分布式光伏承载能力区间分析方法

徐非非，冯 华，覃洪培，文洪君，解志良，叶尚兴，邱 逸

（1. 国网浙江省电力有限公司丽水供电公司，浙江 丽水 323000；2. 浙江大学 电气工程学院，杭州 310027）

0 引言

在能源转型、“双碳”目标及分布式光伏整体推进等战略的驱策下，分布式光伏发展迅猛，在配电系统中的渗透率持续攀升［1-3］。然而，分布式光伏出力具有随机性和波动性［4-5］，其大规模接入给配电网运行带来潮流过载、电压越限、电能质量降低等突出问题［6-9］。因此，亟需考虑分布式光伏出力不确定性，分析配电网分布式光伏承载能力，为分布式光伏合理开发与利用提供有价值的参考信息，以保证海量分布式光伏接入下配电网运行的安全性和稳定性。

配电网分布式光伏承载能力分析，即分析一定系统配置和安全运行约束下，配电网最大可接入的分布式光伏容量［10-11］。随着配电网分布式光伏开发利用工作的不断深入，分布式光伏承载能力分析与评估正成为研究热点。文献［11］在分析配电网承载能力影响因素的基础上，提出一种数据驱动方法来评估各级母线分布式光伏承载能力。为改善传统随机分析方法的性能，文献［12］使用快速排序算法削减重复的光伏安装位置组合，提升了计算效率和评估精度。文献［13］提出一种基于α-cut 的光伏承载能力模糊评估方法，采用区间模型来模拟光伏出力，相比于传统的考虑越限风险的计算方法，其结果保守性有所降低。文献［14］考虑电压上升与电压偏差约束，提出一种基于概率的分布式电源承载能力分析方法，通过两阶段优化算法求解所提非线性模型得到评估结果，并分析了分布式电源类型、负荷增长等因素对承载能力的影响。上述文献均针对光伏承载能力分析进行了深入的研究，但是缺乏对分布式光伏发电功率不确定性的综合考量，导致分析结果精度和方法适用性均无法保证。

为充分考虑分布式光伏发电功率不确定性，有效计算配电网分布式光伏承载能力，本文提出一种配电网分布式光伏承载能力区间分析方法：基于分布式光伏发电系统历史运行数据，利用非参数核密度估计方法对发电功率不确定性进行分析与量化，并应用牛顿法求解对应CL（置信水平）下的分布式光伏出力区间；基于分布式光伏出力区间，建立考虑系统运行约束的配电网分布式光伏承载能力区间分析模型，结合区间分析理论将其分解为乐观子模型和悲观子模型，并通过模型简化与求解得到区间解，有效分析计算配电网分布式光伏最大可接入容量。

1 配电网模型

随着分布式电源、储能等灵活可控设备的大规模接入，传统配电网由“被动”向“主动”转变，具备接纳海量分布式光伏的能力［15］。

1.1 配电网潮流模型

为描述配电网中线路潮流、节点电压及各节点注入功率之间的关系，本文采用配电网Dist-Flow 模型［16］。此外，由于网络损耗一般比线路潮流要小得多，可忽略网损将模型线性化［17］。对于一个具有N个节点的配电网，其潮流方程表示为：

式中：Pij，t和Qij，t分别为t时刻线路ij上流过的有功、无功功率；Pj，t和Qj，t分别为t时刻从节点j注入的有功、无功功率；Ui，t为t时刻节点i的电压幅值；Rij和Xij分别为线路ij的电阻、电抗；Cj为与节点j存在线路连接关系的所有子节点集合。

为确保系统安全运行和供电质量，需要保证线路潮流和节点电压在一定的安全范围内。

1）功率安全约束为：

式中：和分别为线路ij有功功率约束的下界、上界；和分别为线路ij无功功率约束的下界、上界。

2）节点电压安全约束为：

式中：和分别为节点电压幅值的安全下界、上界。

3）与主网交换功率安全约束为：

式中：和分别为配电网与主网有功、无功交换功率，其上标max表示线路安全稳定极限。

1.2 传统分布式电源

传统分布式电源主要为微型燃气轮机发电机组或柴油发电机组，被安装在配电网各节点处，为系统提供一定的有功、无功灵活调节能力。其运行模型为［18］：

式中：和分别为t时刻节点i处传统分布式电源的有功、无功出力，其上标min和max分别表示机组运行有功、无功功率约束的下界、上界；和分别为机组向下、向上功率爬坡能力；Δt为时间间隔；T为优化周期。

1.3 储能系统

系统中安装的储能元件一般以铅酸电池、磷酸铁锂电池、钠硫电池等为主，具备较快的充、放电速率，可为系统运行提供灵活快速的调节能力。其运行约束［19］表示为：

式中：和分别为t时刻节点i处储能系统的充电、放电功率；和分别为节点i处储能系统的最大充电、放电功率；和分别为t时刻节点i处储能系统的充电、放电状态，为0-1变量；ζi，t为t时刻节点i处储能系统的荷电状态，和分别为其下界、上界；ηself、ηch、ηdis分别为储能系统自放电率、充电效率、放电效率；为节点i处储能系统的安装容量。式（15）确保同一时刻储能系统只进行充电或者放电；式（16）表示储能系统荷电状态与充、放电功率之间的关系

1.4 无功补偿元件

为改善配电网电压分布，减小网络传输损耗，系统中往往安装静止无功补偿器和投切电容器组等无功补偿元件［20］。其中静止无功补偿器可产生感性无功功率，且具备连续调节能力，其运行约束［18］可表示为：

式中：为t时刻节点i处静止无功补偿器发出的无功功率；和分别为其最大、最小值。

投切电容器组为离散无功补偿装置，发出感性无功，其数学模型［20］为：

式中：为t时刻节点i处投切电容器组发出的感性无功功率；为单个电容器的额定无功功率；为t时刻节点i处投入的电容器个数；为节点i处电容器组最大可接入的电容器个数。

1.5 分布式光伏发电系统

分布式光伏发电系统逆变器侧输出的稳态有功功率应满足如下约束：

式中：为t时刻节点i处分布式光伏发电系统输出的有功功率；为节点i处分布式光伏发电系统的装机容量。

分布式光伏发电系统逆变器侧输出无功功率可调，可提升配电网分布式光伏承载能力，其运行约束［21］表示为：

式中：为t时刻节点i处分布式光伏发电系统逆变器侧输出的无功功率；和分别为逆变器运行功率因数上、下限值所对应的相位角。

2 考虑不确定性的分布式光伏承载能力区间分析模型

2.1 分布式光伏出力不确定性建模

受太阳辐照度、温度等环境因素的影响，分布式光伏发电系统出力具有不确定性高和波动性强的特征，难以准确预测［22-23］。在本文中，为量化分布式光伏出力不确定性，基于非参数核密度估计［24］方法并结合历史数据，建立分布式光伏出力概率分布。采用以标准高斯函数为核函数的核密度估计方法［25］建立非参数概率分布，以描述和量化特定时间分布式光伏出力不确定性。所得PDF（概率密度函数）可表示为：

式中：Ns为样本数目；h为带宽，是平滑参数；x和Xm分别为随机变量和样本；̂(x)表示分布式光伏出力的PDF；K(⋅)为高斯核函数。

在获得分布式光伏出力非参数PDF 后，相应的累计概率分布函数̂(x)可表示为：

进一步地，可采用式（25）计算CL为(1-α)（α为分位水平）所对应区间的上、下端点：

式中：和分别为置信区间的上、下端点，其对应的分位水平分别为αu和αd；为的逆函数。

显然，累计分布函数为非线性函数，难以直接求解分位数。通过观察可以发现，任意给定x=x'，PDF 值̂(x')非负，且该值恰为累计分布函数̂(x)在x=x'处的一阶导数，非常适合采用数值优化方法求解分位点［26］。本文选用牛顿法，具体求解流程如下：

步骤1：设置初始迭代点x0=xinitial、迭代次数k=0、目标分位水平αtar以及容差ε。

步骤2：迭代更新。

式中：xk为第k次迭代计算得到的结果。

通过牛顿法求解获得对应CL 下的分位数后，分布式光伏有功出力区间可相应表示为：

式中：为分布式光伏出力，是区间变量；和分别为区间的上、下限。类似地，分布式光伏无功出力也可以区间形式描述。

2.2 分布式光伏承载能力区间分析模型

分布式光伏出力具有较强的随机性，过大的配电网分布式光伏安装容量易引起系统运行安全问题；较小的安装容量虽然能够保证系统运行安全，但无法充分利用现有配电网承载能力以支撑分布式光伏开发利用。因此，需要充分考虑分布式光伏出力不确定性和系统运行安全约束，对配电网承载能力进行分析和计算。为此，本文在获得分布式光伏出力区间的基础上，基于区间分析理论建立分布式光伏承载能力区间分析模型，以实现不确定性下配电网分布式光伏最大接入容量分析与计算。

1）目标函数。分布式光伏承载能力分析模型的目标函数为系统各个节点可接入的分布式光伏容量之和，表示为：

式中：J为目标函数。

2）约束条件。该模型中须考虑的约束条件主要包括第1章和第2.1节中描述的配电网、传统分布式电源、储能设备、无功补偿元件及分布式光伏的运行约束。

以z表示区间变量（分布式光伏发电功率占其安装容量的比例）组成的向量，y表示系统中其他决策变量和状态变量构成的向量（包括光伏安装位置及容量、线路潮流、节点电压以及其他设备的运行策略等），则配电网分布式光伏承载能力区间分析模型的紧凑形式可表示为：

式中：A、B、H、D、E、b、g、f均为常系数矩阵或向量；z⊗y表示向量z与y的哈达玛积，表征分布式光伏出力区间；Y为决策空间；Z为区间变量z的约束集合。上述模型约束中包含区间变量，难以应用现有方法直接进行求解。

3 模型转化与求解

根据区间分析理论，上述分布式光伏承载能力分析模型可转化为乐观子模型和悲观子模型［27］，并分别进行求解以获得区间解。其中乐观子模型计算最好情况下配电网分布式光伏最大可接入容量，表示为：

该模型内外层可以合并，实质上是一个单层优化问题，求解相对简单。而悲观子模型则寻找光伏出力最恶劣情况下配电网分布式光伏承载能力，表示为：

上述悲观子模型是一个两层嵌套的“minmax”鲁棒优化问题，优化求解难度大。通过观察发现， 区间变量z仅出现在不等式Hy+D(z⊗y)≤g中，该不等式可进行等价转化［28］，表示为：

式中：zu为z的上界所构成的向量。

上述转化过程的具体含义为：分布式光伏出力水平越高，配电网所允许的最大分布式光伏接入容量必须越小，才能避免系统出现电压越限、潮流过载等问题，因此悲观解必定出现在分布式光伏出力上界处。通过将含区间变量的不等式约束按上述方法进行转化，原悲观子模型可等价表示为：

通过上述过程，原双层嵌套且含有区间变量的悲观子模型被转化为一个混合整数线性规划问题。所提分布式光伏承载能力区间分析模型可直接利用CPLEX、GUROBI等求解器进行求解，最终获得配电网分布式光伏承载能力区间解。

4 算例分析

4.1 测试系统配置

本文首先基于15节点配电系统进行仿真分析，以验证所提方法的有效性。如图1所示，该系统包含1 个15 节点配电网络［29］、3 个传统分布式电源、3 个储能系统、1 个静止无功补偿器和2 个投切电容器组。基于浙江北部实际光伏电站采集的一年历史运行数据，分析分布式光伏出力不确定性并构建其出力区间。其他数据参考文献［13，18，20］。此外，本文还针对浙江丽水某地区实际配电网展开分析计算，以说明所提方法在实际工程中的应用效果。所有的仿真计算均在搭载有Intel i7-10700 CPU和16 GB RAM的计算机上完成，使用YALMIP工具箱在MATLAB 2019a平台上进行建模，并通过商业求解器GUROBI 9.5.2求解。

4.2 分布式光伏出力不确定性量化结果分析

结合历史数据，通过非参数密度估计方法得到夏季、冬季和过渡季3种典型季节下分布式光伏出力的概率分布，正午时刻分布式光伏出力的真实数据分布与核密度估计结果如图2所示。从图2可知，3种典型季节下分布式光伏发电功率均呈现双峰分布特征，而非单峰。同时，PDF 曲线对数据真实分布的近似效果较好，充分说明了非参数核密度估计的优势。

图2 不同典型季节下12：00分布式光伏发电功率核密度估计结果与直方图Fig.2 Kernel density estimation （KDE） results and histograms of distributed PV generation power at 12：00 under different typical seasons

此外，分布式光伏发电功率在夏季主要集中分布在区间［0.10，0.20］ p.u.和［0.60，0.75］ p.u.内，在冬季主要分布在［0.00，0.18］ p.u.和［0.50，0.65］ p.u.两个区间内，在过渡季则主要集中分布在［0.00，0.15］ p.u.和［0.50，0.70］ p.u.两个区间内。不同季节下同一时段分布式光伏发电功率分布特征的区别较为明显，充分说明分季节分析讨论分布式光伏出力不确定性的正确性和必要性。

根据所得非参数核密度估计结果，利用所提计算方法，分别获得了CL 为90%时夏季、冬季和过渡季对应的分布式光伏各小时发电功率区间，结果见表1。由于分布光伏在夜间不发出功率，表中仅列出白天时段所对应的分布式光伏出力区间。相比于直接根据经验给定分布式光伏出力的上、下界，本文所提方法能够更加精确地描述不同典型季节下分布式光伏发电功率的分布特征，可为后续承载能力分析提供良好的数据支撑。此外，通过对比不同季节的分布式光伏出力区间，可以发现夏季分布式光伏出力时间范围更长且区间更宽，过渡季次之，冬季最短。

表1 不同时刻分布式光伏发电出力区间（CL为90%）Table 1 Output power intervals of distributed PV power generation at different hours （CL=90%）

4.3 15 节点配电系统分布式光伏承载能力仿真分析

为了说明所提配电网分布式光伏承载能力分析方法的有效性，对比分季节和不分季节两种场景下配电网分布式光伏承载能力分析结果，如表2所示。相比于不分季节，分季节分析得到的配电网分布式光伏承载能力区间宽度窄3.20%，说明由分布式光伏出力不确定性导致的承载能力波动范围减小，分季节分析可获得更加可靠的承载能力分析结果。此外，区间优化得到的目标函数平均值即为期望值［30］，在本算例中，分季节计算得到的分布式光伏接入容量平均值比不分季节大1.42%，即分布式光伏接入容量期望值更大，说明了分季节分析配电网分布式光伏承载能力的必要性。

表2 不同场景下承载能力计算结果对比（CL为90%）Table 2 Comparison of calculated hosting capacities under different scenarios （CL=90%）

为了分析CL的选择对承载能力计算结果的具体影响，分别选取10%～90%多个CL下的分布式光伏出力区间进行承载能力分析计算，结果如图3所示，不同CL下分布式光伏接入位置（节点）列于表3。由图3 可知，随着CL 增长，分布式光伏承载能力平均值和变化范围均增大。这是由于CL越高，分布式光伏出力波动区间越大，对分布式光伏承载能力分析结果的影响也越大。由表3中所列分布式光伏安装位置可知：乐观情形下分布式光伏安装在具有灵活调节设备的节点或支路，可以通过调节相应设备有功、无功输出以支撑分布式光伏接入；悲观情形下分布式光伏倾向于安装在配电网线路末端，节点11和15负荷水平较高，在这两个节点接入的分布式光伏发电功率大部分可在本地消纳，不容易引起系统电压越限、潮流过载等安全问题。

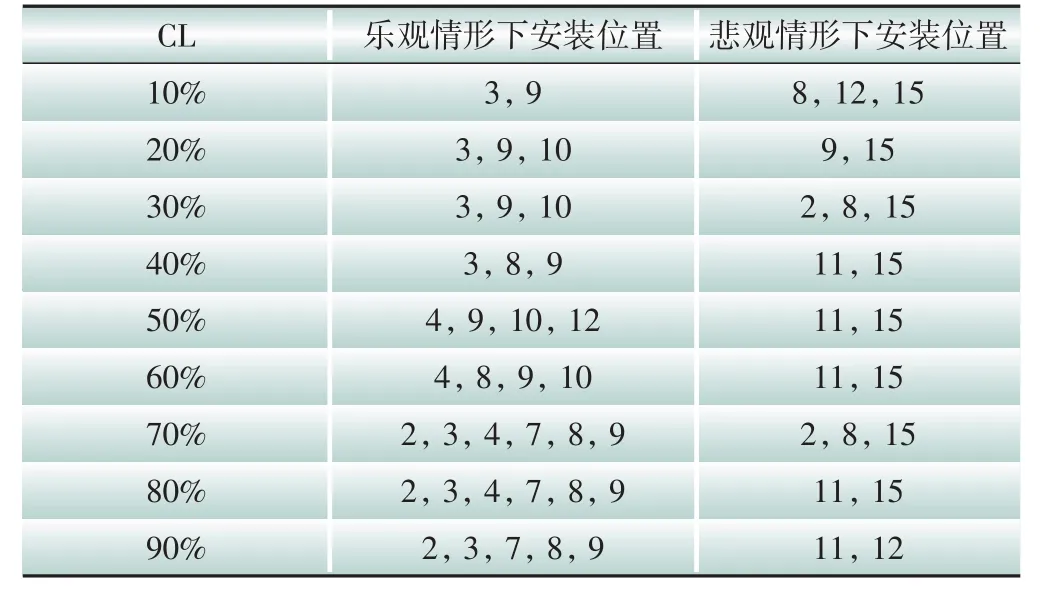
表3 不同CL下分布式光伏安装位置Table 3 Installation locations of DPV at different CLs

图3 不同CL下配电网分布式光伏承载能力分析结果Fig.3 Analysis results of DPV hosting capacity in distribution networks at different CLs

4.4 分布式光伏承载能力影响因素分析

由4.3节分析可知，配电网中灵活调节设备安装容量和负荷大小对配电网分布式光伏承载能力存在影响，有必要针对这些因素展开具体分析。分别设置接入3 500 kW、5 000 kW、6 500 kW 容量的传统分布式电源，并设置90%、100%、110%负荷水平，研究传统分布式电源接入容量和负荷水平对分布式光伏承载能力的影响，结果如图4、图5 所示（CL 为90%）。在乐观、悲观情景下，配电网分布式光伏承载能力均随传统分布式电源接入容量增加而减小，随负荷水平的增加而增大。这是由于负荷水平增长，系统分布式光伏接纳能力增强，进而增加了分布式光伏承载能力。而传统分布式电源的接入容量增大则挤占了分布式光伏可接入容量的增长空间，进而减小了配电网分布式光伏承载能力。

图4 不同系统配置下分布式光伏承载能力（乐观情景）Fig.4 DPV hosting capacities with different configurations（under optimistic scenarios）

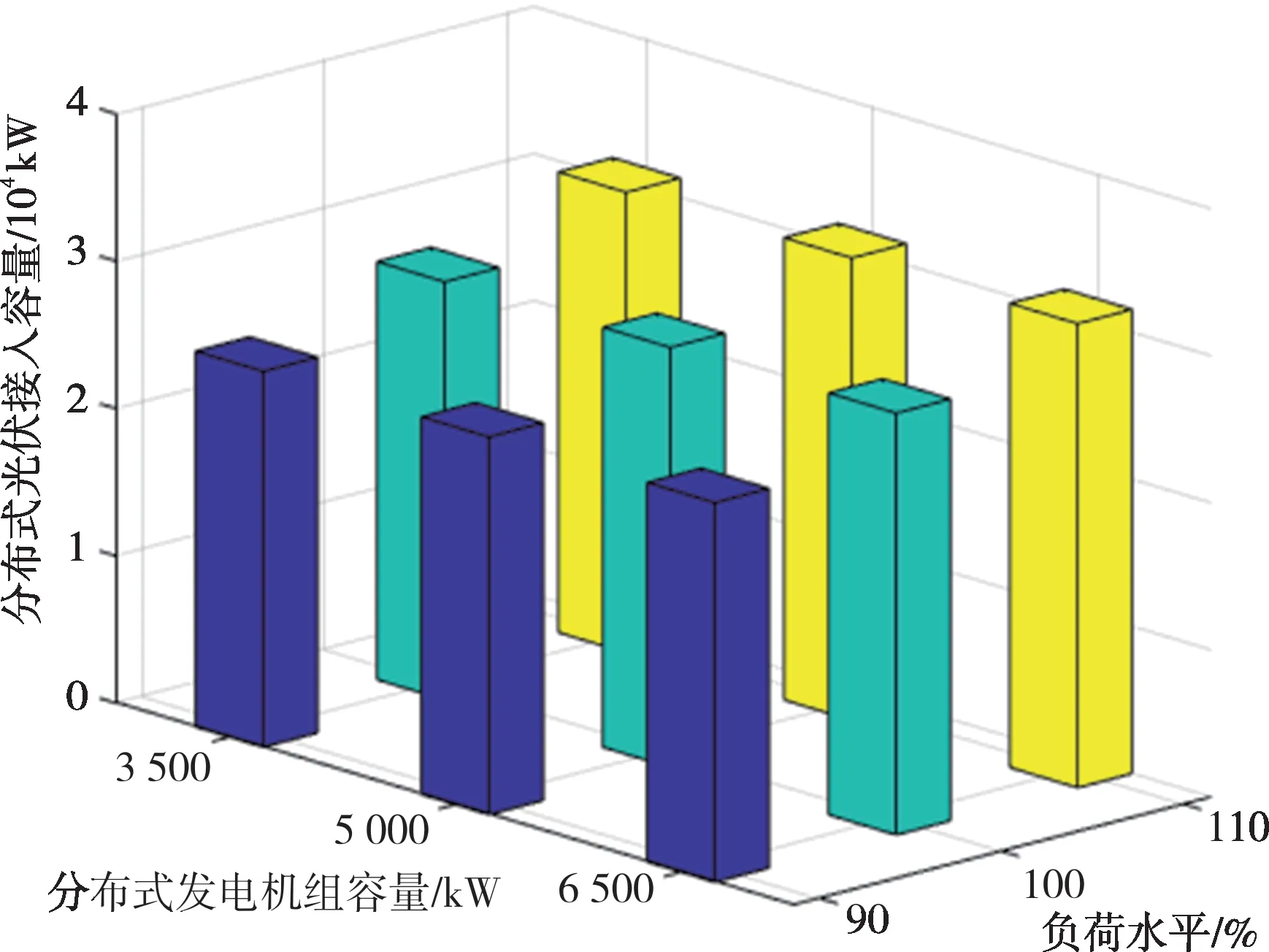
图5 不同系统配置下分布式光伏承载能力（悲观情景）Fig.5 DPV hosting capacities with different configurations（under pessimistic scenarios）

4.5 实际配电网分布式光伏承载能力仿真分析

为体现本文所提方法在实际工程中的应用价值，针对浙江省丽水市某10 kV配电网展开了分布式光伏承载能力计算与分析。该系统共有22 个节点和21 条线路，接入1 个380 kW 光伏电站和1 个1 000 kW水电站。系统最大有功负荷为4.58 MW，最大无功负荷为2.63 Mvar。该配电网拓扑结构如图6所示。针对该系统的分布式光伏承载能力分析结果如表4所示（CL 为80%）。乐观和悲观情景下分布式光伏承载能力计算结果分别为61.87 MW和17.78 MW，说明当分布式光伏出力在80%置信区间内波动时，系统最大可接入的分布式光伏容量在［17.78，61.87］ MW 范围内变化。两种情景下，分布式光伏接入位置均在靠近变压器或联络线出口处，以利用配电线路输电能力，将无法在本地消纳的光伏电力输入上级电网或通过联络线供给临近配电网。综上所述，本文所提方法可应用于分布式光伏出力不确定性下的实际系统承载能力分析，量化承载能力变化范围并给出相应接入位置。

表4 实际系统分布式光伏承载能力计算结果（CL为80%）Table 4 The calculated DPV hosting capacities （CL=80%）

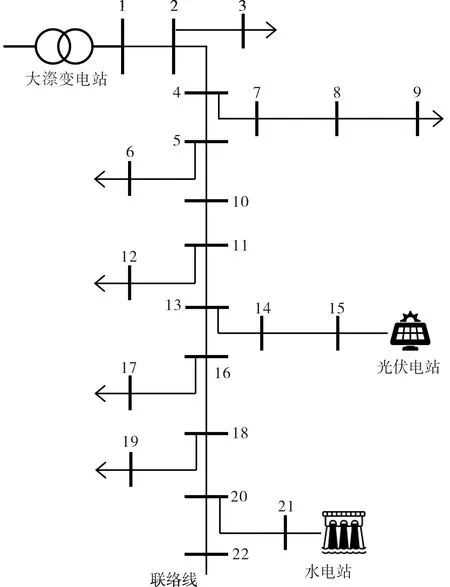
图6 浙江省丽水市某10 kV配电网拓扑Fig.6 Topology of a 10 kV distribution network in Lishui，Zhejiang Province

5 结语

本文基于历史数据和非参数核密度估计方法，构建了反映分布式光伏出力长时间尺度波动特征的功率区间，提出考虑不确定性的配电网分布式光伏承载能力区间优化模型，通过求解对应的乐观和悲观子模型，得到分布式光伏承载能力计算结果。通过基于15 节点配电系统和浙江省丽水市某10 kV 配电网的仿真计算与分析，得到如下结论：

1）分布式光伏发电功率在不同季节存在明显不同的分布规律，本文所提方法可利用非参数核密度估计方法有效量化分布式光伏出力不确定性，且可以计算给定CL下分布式光伏的出力区间。

2）本文所提方法充分考虑了分布式光伏出力的不确定性，利用区间优化方法有效量化光伏发电功率波动下配电网分布式光伏承载能力变化范围。在15 节点配电系统和浙江丽水某10 kV 配电网上的对比分析结果验证了所提配电网分布式光伏承载能力分析方法的有效性。

针对该研究，未来将进一步考虑分布式光伏出力相关性、负荷不确定性及电压质量等因素，更加精确地量化和分析配电网分布式光伏承载能力，并尝试针对如何有效提升配电网分布式光伏承载能力这一命题进行拓展性研究。