基于三种不同计算模式的高层建筑结构变形数值模拟研究

杨 眉

（陕西职业技术学院，陕西 西安 710038）

0 引言

高层建筑结构在施工和使用过程中都会进行变形分析，一方面是评价结构的受力情况，另一方面可以预测结构的变形发展趋势。在高层建筑修建之前，为了有效分析和预测结构的变形情况，往往采用数值模拟的方法。由于实际施工情况复杂，影响因素较多，单一的数值计算模式往往难以精准分析高层结构变形情况。基于此，本文以某高层建筑项目为例，采用三种不同的数值计算模式进行分析，并将数值计算结果与施工监测数据进行对比分析，以期有效预测结构的变形情况，为设计规划、施工建设以及长期使用提供依据。

1 工程概况

案例工程施工面积达27.8 万m²，地下共3 层，塔楼共90 层，大楼高428m，加上屋顶幕墙构造实际高度共计445m。塔楼的西面是一片商业裙楼并与塔楼形成一体，是一栋含有商业办公、休闲娱乐以及酒店等项目的超高层综合楼。塔楼体系结构是以包含加强层的钢筋混凝土核心筒和钢管混凝土框架结合的混合体系结构，伸臂桁架加强层搭设在43～44层与70～72层。该塔楼的钢筋混凝土核心筒竖向大体分三次往北面收缩，塔楼南面的框架柱整体往北面倾斜2°。结构整体效果以及施工现场情况分别见图1和图2所示。

图1 结构整体效果图

图2 施工现场示意图

2 数值模型建立

为了精确掌握项目作业过程中和投入使用期间工程结构改变以及内力变化状况，使用有限元软件ETABS进行建模，重点对工程结构、施工材料以及使用荷载等几方面进行模拟，并将材料的时变效应因素也计算在内，以此模拟出工程结构的受力改变和内力转化状况。

2.1 材料定义

有限元软件ETABS 的应用，使得施工人员可以很方便地了解到工程所需的符合规范的原材料。软件中混凝土的等级选取范围大、类型多，钢材料包括Q235和Q345 等，所有材料性质都选取线弹性。在此基础上，使用者可以按照实际需求选取混凝土或钢材料的型号和特性。该工程项目中，实际选用的混凝土强度是C30和C60，钢结构是Q235和Q345[1]。

2.2 结构的模型化与基本假定

在该工程数值模型中，假设受到自重作用，在基础搭建后沉降基本完成并且不会改变上部结构的位移，结构起初位置移动为零。应用有限元结构软件对工程实施分析时，必须按照下述模型化的原则来实现结构模型化：在开始分析建筑结构时，因为各单元之间的受力关联特征直接影响着分析的结果，所以想要获得准确的分析数据，就必须要合理规划各单元之间的联系，开始组建结构模型时，重点选取简化后的结构组件。模型化结构荷载是采取了结构参数的样式表现结构在现实工程中承受的荷载，由于结构在工程实施过程中受到许多种类不同的荷载，如果能够设计与现实相差不多的荷载，就可以得到较为准确的模拟结果。

3 三种数值计算模式

采 用ACI209R-1992 和Bazant-BawejaB3、CEBFIP90三种不同的计算模式模拟建筑结构的位移情况。有限元结构分析软件ETABS可以对施工过程进行分阶段模拟，能够对比分析外框筒-内核心筒-伸臂桁架结构的位移情况。

3.1 ACI209R-1992计算模式

通过对ACI209R-1982 模式进行改造后，形成了ACI209R-1992 模式，主要变化是在分析环境湿度、构件大小以及混凝土配比因素之外，添加了相对湿度、养护方式以及加载龄期等。

ACI209R-1992 计算模式函数表达式包括ACI 模型徐变函数表达式和收缩应变表达式。

ACI模型徐变函数表达式如下：

式中：K1——混凝土的加载龄期影响系数，K1=；

K2——环境相对湿度的影响系数，K2=1.27-0.0067IRH（IRH＞40%）；

K3——混凝土构件平均厚度的影响系数；

K4——混凝土稠度的影响系数，K4=0264.082.04；

S——新鲜混凝土的坍落度，mm；

K5——细骨料含量影响系数，K5=0.88+0.0024f；

F——细骨料（f＜4.8mm）占总骨料分率；

K6——空气含量影响系数，K6=0.46+0.09Ad≥1；

Ad——新鲜混凝土中所含空气的体积，%。

ACI模型收缩应变表达式如下：

式中：（εsh）max——应变终值。

3.2 Bazant-BawejaB3计算模式

Bazant-BawejaB3 计算模型中通常用徐变函数去表示单位应力下的总应变，分为基本徐变和干燥徐变两种，其中基本徐变和干燥徐变的计算公式如下：

徐变函数的表达式为：

基本徐变度：

干燥徐变量：

式中：q1——单位应力产生的瞬时应变；

q2,q3,q4,q5,H(t),H(τ),E(τ)是与构件材料组成相关的系数。

收缩应变表达式为：

时间曲线：

式中：εshx——收缩终极值；

kh——与环境相对湿度有关的函数；

τsh——与构件尺寸有关的函数。

Bazant-BawejaB3 模型采用英制单位，长度单位为inch(linch-25.4mm)，材料含量单位为bft-3(lbft-3=16.03kgm-3)，混凝土强度单位为psi(lpsi=6895pa)。

3.3 CEB-FIP90计算模式

CEB-FIP90 模型在进行收缩变形的计算中考虑了以下各方面因素：龄期为28d 时混凝土的平均抗压强度，混凝土构件暴露在环境中的平均相对湿度，水泥的种类、养护时间等。其收缩变形计算表达式为：

εcso——名义收缩系数，εcos =[ 160+10βsc(9-0.1fcm) ]×10-6βRH；

βRH（h）为湿度修正系数，表达式为：

式中：V/S——构件体表比，mm；

t——混凝土龄期；

tc——混凝土湿气养护结束时的龄期；

t1——常量，值为1。

4 数值计算结果分析

采 用ACI209R-1992 和Bazant-BawejaB3、CEBFIP90 收缩徐变计算模式模拟分析建筑结构的核心筒剪力墙和外筒柱的竖向位移、竖向位移差和水平位移的数据，不同计算模式模拟的数据见图3～5所示。

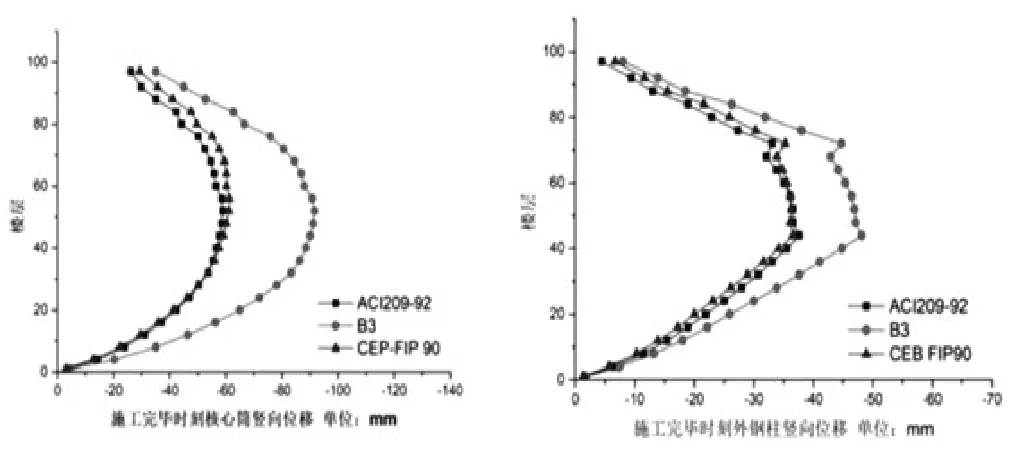
图3 三种计算模式施工完毕时刻结构竖向位移对比

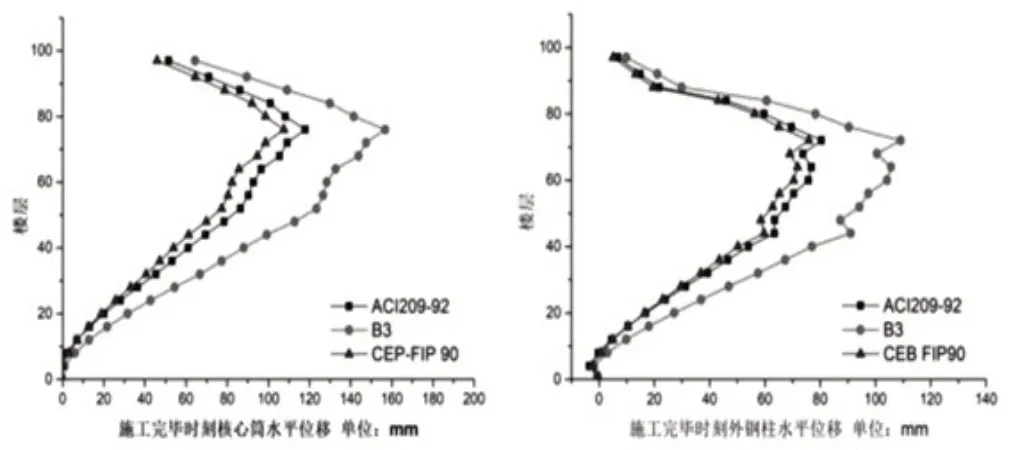
图4 三种计算模式施工完毕时刻结构水平位移对比

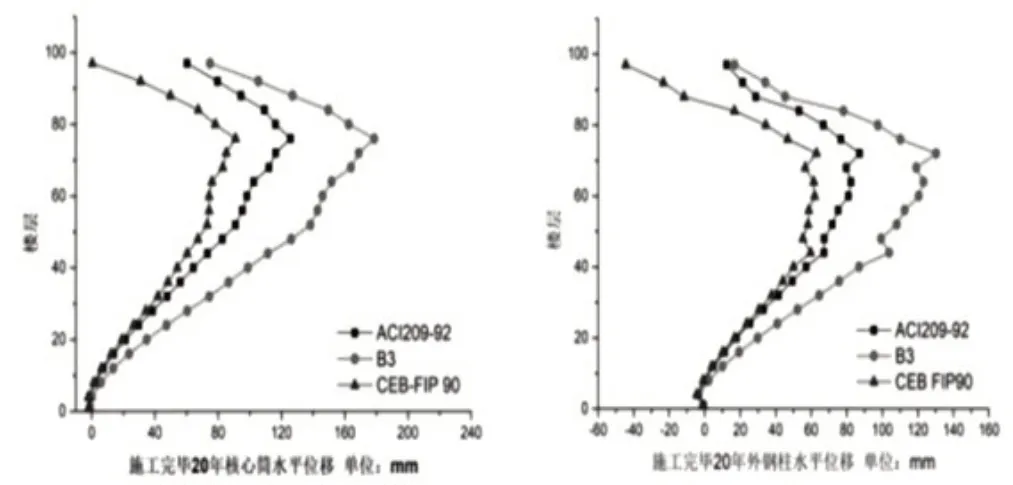
图5 三种计算模式施工完毕20年结构水平位移对比

从3 个图中不难发现：结构的竖向位移量表现为中间大两端小的趋势，且位移量随着建筑层数的增加呈现出先变大后变小的规律，在这里我们可以称之为“鱼腹型规律”，三种计算模式下模拟测得的核心筒和外框筒柱最大的竖向位移发生的位置都是在中间楼层。三种模式测得的结构竖向位移、竖向位移差以及水平位移存在差异，建筑工程主体结构竣工后，三种模式计算下的数据依次表现为Bazant-BawejaB3＞ACI209-92＞CEB-FIP90，其中ACI209R-1992 和CEBFIP90 计算模型下的数据结果相近；在工程竣工20 年时刻，通过三个模拟模拟数据显示结果差异较大，其中Bazant-BawejaB3 和CEB-FIP90 测得的竖向位移量的结果比较接近，CEB-FIP90 和ACI209R-1992 测得的水平位移量的结果相近。

5 数值计算与施工监测的数据对比分析

对于超高层结构建筑的设计和施工往往通过施工模拟数据作为参考依据。施工模拟是基于实际结构简化的基础上建立结构模型进行分析的，由于施工现场的不确定性和复杂性，许多载荷和非载荷因素根本无法提前预见，有时软件也无法对一些复杂的因素进行模拟分析，因此就存在施工模拟数据和实际监测的数据不一致的情况。所以，为了保障建筑结构的安全性，就需要在施工过程中不断监测结构的位移情况和内力变化情况[2]，并与数值模拟结果进行对比。

5.1 施工模拟与施工监测的工况

对该楼核心筒剪力墙和外框柱的水平位移数据进行模拟分析和过程施工监测，不仅可以验证数值计算的准确性，也可以分析施工监测中数据源的精确性。现场施工监测可以得到建筑结构施工开始到核心筒施工再到顶部楼层等监测楼层核心筒和外框柱的水平位移。结合该工程的施工进度并考虑数据量较大的原因，对比分析了19M 层和31M 层的水平位移情况，如图6、图7 所示。对比施工方提供的核心筒及外框架位移数据，一方面选取核心筒角点1、3、4、6 的位置，另一方面选取外框架角点7、9、12、14 位置，将实测数据和模拟结果进行对比分析，Y正向为结构正北方向。

图6 19M层水平位移对比

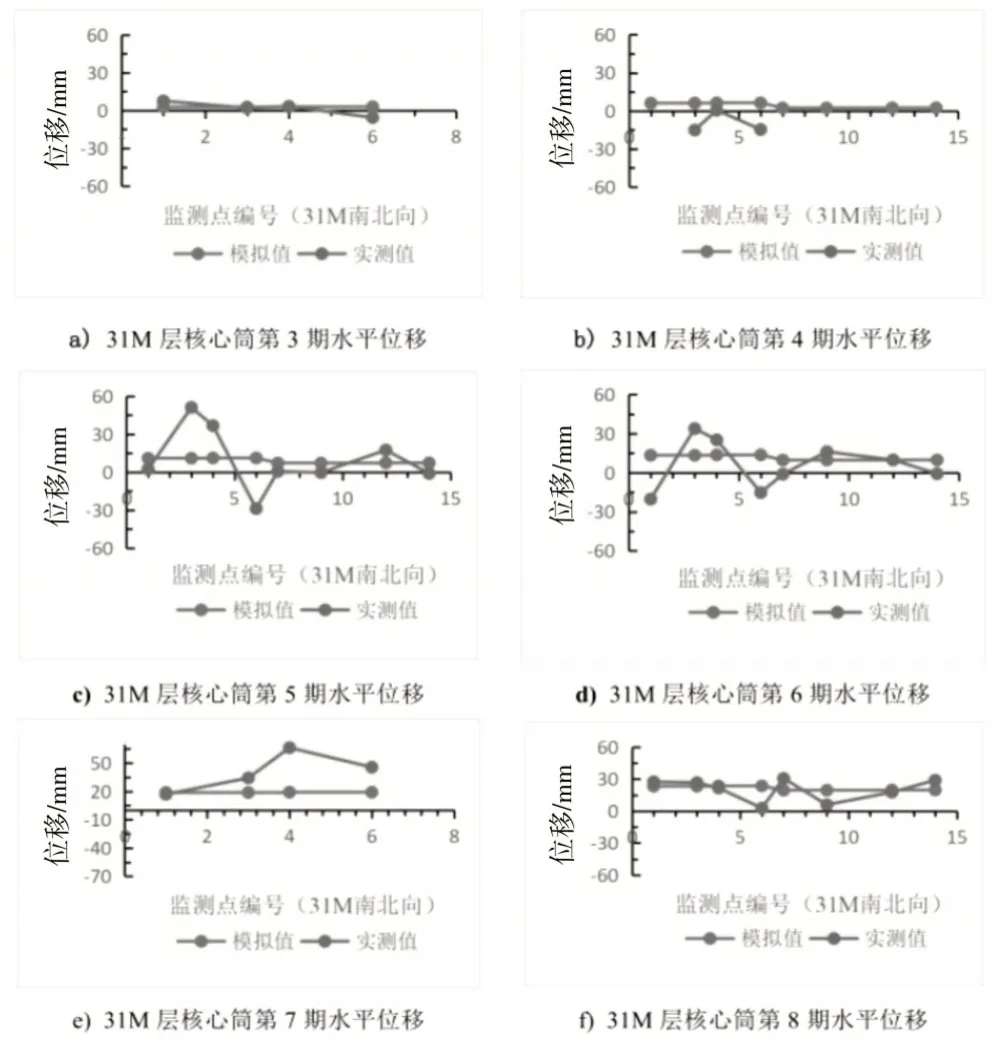
图7 31M层水平位移对比

5.2 施工模拟与施工监测结果对比

通过对比分析施工现场实测数据和施工模拟数据发现：两者测得的结构位移趋势大致是吻合的，但还存在一定的差异，如图6和图7所示。施工现场测得的数据和模拟分析的数据存在差异主要有两方面的原因：一方面是受施工组织的影响，在进行模拟分析时，通常都会按照原计划的施工速度进行计算，完成一层楼施工按照一周时间模拟，封顶时工期按照854d 模拟，核心筒超前外框架施工层数固定为10 层，同层柱与梁同时生成。而在实际的施工现场，核心筒超前外框架施工层数不是固定不变的，每层的施工天数也是随时会发生变化，也有可能因为某些客观因素导致停工等。另一方面是受施工荷载的影响，在进行施工模拟分析时，荷载都是固定的，如包含结构自重的载荷，另外还会有一个2kN/m²的均布面荷载，风荷载等水平荷载不会被模拟。但是在施工现场实测时，出现的载荷是多种多样的，有时还会出现一些不确定的集中载荷或者其他动力载荷，在实际施工过程中总会遇到一些不确定的外界因素导致结构变形，而这些因素在模拟分析时又不会被模拟到，因此两者分析得出的数据出现差异也就在合理范围内[3]。

6 结束语

综上所述，本文采用ACI209R-1992 和Bazant-BawejaB3、CEB-FIP90三种不同的计算模式对高层建筑结构变形情况进行了数值模拟分析，虽然三种计算模式得到的结果存在差异，但是可以确定的是三种计算模式得到的结果与实际施工过程中结构变形的趋势是一致的。通过对数值计算的结果与施工监测的数据进行对比可知，两者测得的结构位移结果数据基本相似，这在很大程度上说明数值模拟分析的数据精确度较高。虽然模拟分析已全面考虑了施工现场各种可能出现的原因，如混凝土材料收缩徐变效应和施工的顺序、荷载、速度等，但是基于本研究的施工工程规模大、结构复杂、施工难度系数高以及潜在变化多等特征，加之施工模拟分析软件并不可能将全部的因素模拟进去，所以还存在不足之处，今后还应进行更深入的研究。