拉弯耦合作用下平行钢丝索断丝受力研究
杨建喜 赵金炎 费宏宇 孙全胜













摘 要:为研究拉弯耦合作用下平行钢丝索断丝力学行为,依据文献试验数据建立平行钢丝索弯曲精细化有限元模型,并通过试验数据验证,进一步建立拉弯耦合作用下平行钢丝索断丝有限元模型,研究钢丝断裂后平行钢丝拉索跨中截面变形和应力不均匀分布规律。研究结果表明,拉弯耦合作用下平行钢丝索数值模拟结果与试验数据相一致;预拉力平行钢丝拉索断丝后,周围剩余完好钢丝出现应力重分布现象,越靠近断丝位置的钢丝应力越大,随着断丝数量的增加,剩余完好钢丝应力也增加;在断丝后,影响简支边界条件平行钢丝索断丝处变形大小的因素由大到小依次为拉弯耦合作用、预拉力作用、两端自由。
关键词:拉弯耦合作用;平行钢丝索;断丝;变形;应力重分布
中图分类号:U443.31;U441+.4 文献标识码:A 文章编号:1006-8023(2023)06-0177-11
Broken Wire Mechanical Behavior of Parallel Steel Wire Cable under Combined Tension-bending
YANG Jianxi, ZHAO Jinyan, FEI Hongyu, SUN Quansheng
(School of Civil Engineering and Transportation, Northeast Forestry University, Harbin 150040, China)
Abstract:In order to study the mechanical behavior of parallel steel wire cable breakage under the action of tension-bending coupling, based on the literature test data to establish parallel steel wire cable bending refinement finite element model, and through the verification of the test data, to further establish parallel steel wire cable breakage finite element model under the action of tension-bending coupling, and to study the deformation of parallel steel wire cable spanning the cross-section of the steel wire breakage and the law of non-uniform distribution of stresses. The results showed that the numerical simulation results of parallel steel wire cable under the action of tension-bending coupling were consistent with the experimental data; after the pre-tension parallel steel wire cable broke, the stress redistribution phenomenon occurred around the remaining intact steel wires, the closer to the location of the broken wire the greater the wire stress, with the increase in the number of broken wires, the remaining intact steel wire stress also increased; after the wires broke, the factors affecting the deformation of the simply supported boundary conditions parallel steel wire cable breakage size in descending order were tension-bending coupling effect, pre-tension effect, and free ends.
Keywords:Tension-bending coupling action; parallel wire rope; broken wire; deformation; stress redistribution
收稿日期:2023-06-25
基金項目:黑龙江省交通运输厅科技项目(2020HLJ018)。
第一作者简介:杨建喜,博士,讲师。研究方向为桥梁加固与评定。E-mail: yangjianxi@nefu.edu.cn
引文格式:杨建喜,赵金炎,费宏宇, 等. 拉弯耦合作用下平行钢丝索断丝受力研究[J]. 森林工程, 2023, 39(6):177-187.
YANG J X, ZHAO J Y, FEI H Y, et al. Broken wire mechanical behavior of parallel steel wire cable under combined tension-bending [J]. Forest Engineering, 2023, 39(6):177-187.
0 引言
吊杆作为吊杆拱桥的重要受力和传力构件,将桥面系的荷载传递到拱肋,是传递荷载的纽带。随着我国交通行业的发展迅速,在交通运输系统中,吊杆拱桥的建造数量也随之大幅增加,迄今为止,我国建成的吊杆拱桥达400 座以上。目前世界上已经建成的最大跨径吊杆拱桥是由我国在2020年12月建成通车的广西平南三桥。近些年来,由于吊杆断裂发生的拱桥垮塌事故屡见不鲜,如四川宜宾小南门大桥(2001年)、新疆孔雀河大桥(2011年)、福建武夷山公馆大桥(2011年)、四川攀枝花金沙江大桥(2012年)、中国台湾宜兰南方澳跨港大桥(2019年)和太原南中环桥(2022年),这些事故均造成不同程度的人员伤亡。在拱桥长期服役过程中,由于吊杆护套破损,导致索内钢丝会产生不同程度的锈蚀。而在温度荷载和车辆荷载产生的振动作用下,吊杆锚固端会出现严重的局部弯曲现象,导致吊杆局部受力不均匀和增大效应,吊杆护套和最外圈钢丝长期处于高应力状态,在长期的拉弯耦合作用下,吊杆锚固端会产生机械疲劳,最终在腐蚀和高应力耦合作用下导致内部钢丝断丝,断丝后剩余钢丝应力发生重分布,断丝周围处钢丝受力更不利,随着断丝数目的增加,最终导致吊杆整体破断。
现阶段对拉吊索的受力性能研究较多,大多集中在拉索断丝前拉索应力的变化,而且钢绞线拉索研究偏多。柏伟从钢丝锈蚀特点出发,根据钢丝锈蚀检测数据,研究了点蚀对钢丝力学性能的损伤,并建立了以拉索极限承载力和疲劳寿命作为拉索失效判定指标的在役拉索剩余寿命分析模型。在拉索断丝方面的研究,吴志杰等利用有限元法分析了钢绞线的破坏模式,但未对断丝后索结构应力重分布进行分析。张杰建立了 7 絲1 860 级钢绞线有限元模型并与试验对比验证,得到了 7 丝钢绞线单根钢丝断裂后对其他钢丝的影响。综上所述,现阶段对拉吊索的受力性能研究较多,大多集中在拉索断丝前拉索应力的变化,而且钢绞线研究偏多,对于平行钢丝索断丝后平行钢丝索应力分布及承载能力的影响研究相对较少,还有待完善。Montoya 等提出了一种确定拉吊索安全性的方法,是第一个通过有限元模型来预测拉索锈蚀失效过程的方法,有限元结果表明一根钢丝的锈蚀破断会导致周围钢丝承受应力增大,最终导致整索失效。Maljaars 等认为钢丝制作过程中会产生初始损伤,疲劳裂纹是从这些初始损伤处开始发展的,甚至导致最终的断丝,随后以某实际桥梁为例,提出了断丝拉索失效评估方法。Karanci 等根据以往钢锈蚀速率的试验数据,建立了拉索的时变锈蚀速率模型,能够预测拉索的年锈蚀速率。Milone 等对钢丝绳锈蚀研究进行了全面总结,并在以往的研究基础上对钢丝绳合理的疲劳状况和强度评估作了进一步研究。
本研究利用 ANSYS Workbench 软件建立平行钢丝索拉弯有限元模型并结合试验加以验证,然后考虑腐蚀断丝,研究预拉力、无预拉力以及拉弯耦合作用情况下,平行钢丝索钢丝断裂对钢丝变形和应力重分布的影响,为后续拉索的安全评定提供依据。1 平行钢丝索拉弯有限元模型的建立和试验验证1.1 基本假设
在建立平行钢丝索的精细化有限元模型之前,作如下基本假定:
1)平行钢丝索内部高强钢丝排列方式为对称正六边形;忽略绕包带与钢丝、护套与绕包带之间的接触摩擦作用。
2)允许平行钢丝索内所有钢丝在钢丝索的弯曲变形过程中发生滑移;钢丝与钢丝之间采用线—线接触,钢丝与护套接触部位采用线—面接触;同一平行钢丝索中钢丝间的摩擦系数相同、钢丝与护套间的摩擦系数相同。
3)模型不考虑钢丝塑性情况;假定护套材料相同,所有钢丝采用同种材料;平行钢丝索内部钢丝在弯曲过程中始终处于弹性阶段。
1.2 有限元模型的建立
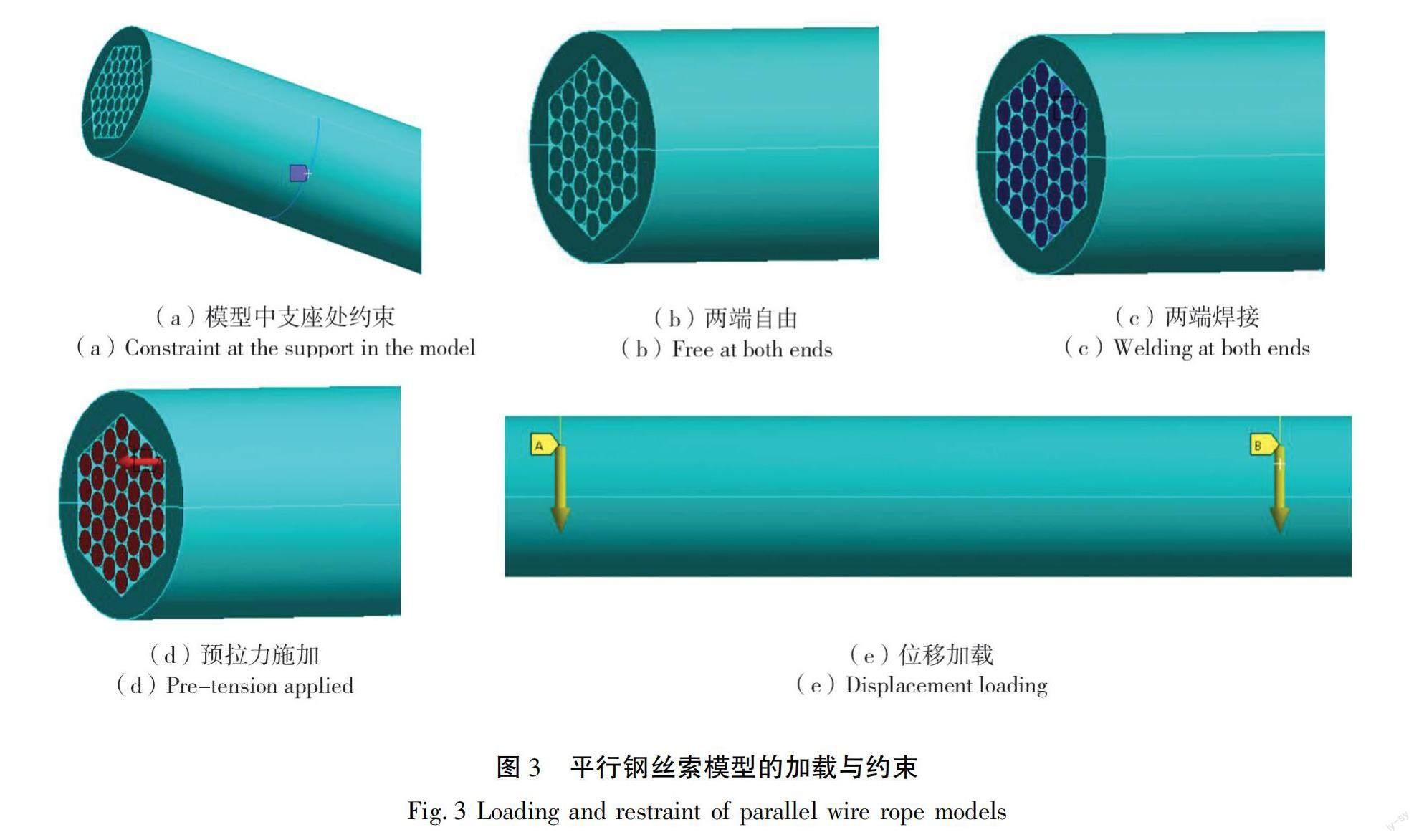
根据文献[16]中平行钢丝索的简支抗弯刚度试验如图1所示,通过有限元软件ANSYS Workbench建立平行钢丝索的三维有限元模型时,平行钢丝索考虑3种不同的边界条件:1)两端自由:钢丝索内部钢丝允许滑动,如图1(b)所示;2)两端焊接:钢丝索端面处不能发生自由滑移如图1(c)所示;3)两端施加预拉力:钢索一端锚固,另一端焊接销铰结构后施加预拉力,如图1(f)所示。
平行钢丝索是将奇数的高强钢丝以高度对称正六边形平行布置、绑扎紧实,然后热挤高密度聚乙烯(High Density Polyethylene,简称HDPE )护套作为保护层。为了与文献已完成试验数据进行对比验证,钢丝索长度选用与试验相同的1 050 mm。以37 φ7平行钢丝索为例,根据平行钢丝索的结构特点,先绘制1/4钢丝束底面,通过2次镜像操作得到完整37 φ7平行钢丝束底面,再绘制厚度为7 mm的圆环作为护套的底面。对底面进行凸台拉伸,建立平行钢丝索的几何模型。钢丝采用Solid186单元。
网格划分由2部分构成,分别是平行钢丝束的网格划分和护套的网格划分。进行钢丝束面网格尺寸划分,选用Multi Zone选项;护套的网格划分是先对一端护套内六边形进行线网格划分,然后在扫掠选项中填写尺寸为10 mm,平行钢丝索底面网格划分如图2(a)所示,护套网格划分如图2(b)所示。
有限元模型中的钢丝索主要部件的物理参数见表1和表2。
模型选择与试验相同的简支梁力学模型进行荷载及约束施加。模拟支座边界条件时,在一端护套上将X、Y、Z方向自由度均约束为0;另一端约束X、Y方向自由度为0,释放Z向自由度,如图3(a)所示。两端自由情况下不对平行钢丝索做边界条件的施加,如图3(b)所示。两端焊接是将所有钢丝端面进行节点耦合并利用刚性面来模拟焊接,如图3(c)所示。施加预拉力情况是将一端所有钢丝端面所有方向自由度约束为零,另一端先进行节点耦合再施加Z向拉力,模拟预拉力,如图3(d)所示。位移荷载的施加与试验相同,在1/3跨度处护套上施加位移荷载,加载长度与试验中的加载装置相同。在此前拉吊索的弯曲性能研究中,大多都是垂直于正六边形边的方向进行加载,本研究则是对正六边形的角点方向进行加载,加载情况如图3(e)所示。
1.3 平行钢丝索有限元模型验证
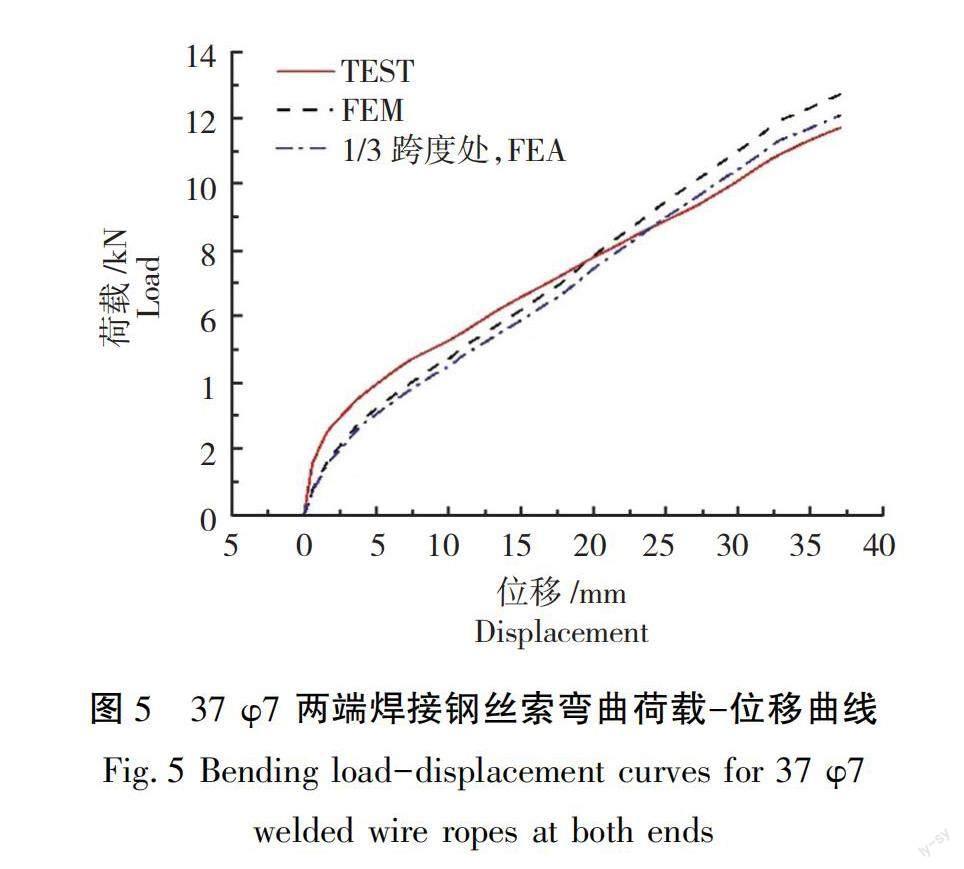
以37 φ7平行钢丝索为例,分别以两端自由和两端焊接的边界条件建立精细化有限元模型,通过对抗弯刚度试验和文献[16]中有限元模型的计算结果与本研究中精细化有限元模型的计算结果进行对比分析,验证了平行钢丝索精细化有限元模型的正确性。由于文献中试验得出的数据是钢丝索荷载和位移的关系曲线,而模型是通过施加位移荷载来实现平行钢丝索弯曲的,故通过ANSYS Workbench中结果后处理模块,得到1/3 跨度处位移加载时的截面反力也就是发生此位移时所需的弯曲荷载大小,由此来绘制弯曲荷载-位移曲线与已有数据进行对比来验证有限元模型的正确性,结果对比如图4和图5所示。(图中荷载-位移曲线分别代表如下含义:TEST为抗弯刚度试验数据;FEM为文献[16]中有限元模型计算结果;FEA为本文精细化有限元模型计算结果。)
从图4和图5可以看出,有限元计算结果绘制的弯曲荷载-位移曲线与文献曲线趋势一致,说明规律基本一致,即有限元建模是合理的。弯曲荷载-位移曲线大致呈现为前期斜率大,后期斜率小的双
折线,与试验中随着位移荷载增加,弯曲荷载的增量减小现象一致,这是由于前期弯曲荷载的施加导致内部高强钢丝发生挤压,使得摩擦阻力增大,同时使得平行钢丝索的弯曲刚度增大,使得加载初期的平行钢丝索更难被弯曲。而在加载的后期,从双折线第二段开始时,两端焊接的平行钢丝索相较于两端自由的平行钢丝索,由于两端自由的钢丝索在加载过程中钢丝可以向自由端发生位移从而减小钢丝索内部挤压程度,两端焊接导致钢丝索端部位移受到约束,而使得钢丝索内部钢丝挤压程度更大,故发生相同位移时所需的弯曲荷载明显更大。2 锈蚀平行钢丝索断丝后在拉弯耦合作用下受力性能分析2.1 平行钢丝索断裂过程分析
假设当平行钢丝索护套刚出现破损时,平行钢丝索内部的高强钢丝未受到环境中腐蚀性因子的腐蚀,即高强钢丝未出现破损锈蚀的情况,损伤为0,此时钢丝的抗拉强度均为σ,高强钢丝拉应力σ<σ。随着腐蚀性因子逐步向平行钢丝索内部扩散,腐蚀性因子出现在高强钢丝周围,越接近护套破损处的高强钢丝,被腐蚀速度越快,腐蚀程度越严重。高强钢丝一旦发生腐蚀,其抗拉强度和弹性模量均会出现不同程度的下降,腐蚀后的第i根高强钢丝的抗拉强度为σ,σ随着时间和腐蚀程度的增加而减小。随着腐蚀性因子向平行钢丝索内部进一步扩散,高强钢丝之间缝隙中的腐蚀性因子越来越多,故高强钢丝的腐蚀速度也会越来越大。
随着平行钢丝索内部高强钢丝腐蚀量的逐渐增加,假设第j根钢丝腐蚀最为严重,当其抗拉强度σ和所受的拉应力σ相等,即σ=σ时,第j根钢丝就会断裂,其他钢丝仍继续工作,会发生应力的重分布,使得剩下的所有钢丝所承受的拉应力增大。若在应力重分布后,剩余的高强度钢丝均为未出现断裂的情况,则表明其所受的拉应力均未达到其抗拉程度,σ<σ,剩余的高强钢丝将共同受力。随着腐蚀的进一步加剧,平行钢丝索内高强钢丝的抗拉程度σ将会进一步下降,直到未断裂的高强钢丝中腐蚀最为严重的一根的抗拉强度σ等于拉应力σ时,钢丝将发生断裂,接着继续发生应力重分布。如此往复循环,直到平行钢丝索所受的力F等于其最大承载力F时,平行钢丝索将会迅速断裂、失效。
2.2 平行钢丝索断丝有限元模拟
2.2.1 平行钢丝索内钢丝编号及断丝位置确定
以 37 φ7 平行钢丝索为例对平行钢丝索断絲后的力学性能进行研究,为方便研究内部钢丝断丝后各钢丝的应力变化,对平行钢丝索内部钢丝进行编号,将钢丝分为7组,第1组由一根钢丝组成编号为1-1,第2组编号为2-1至2-3,第3组编号为3-1至3-5,以此类推,平行钢丝索内部钢丝详细编号如图6所示。
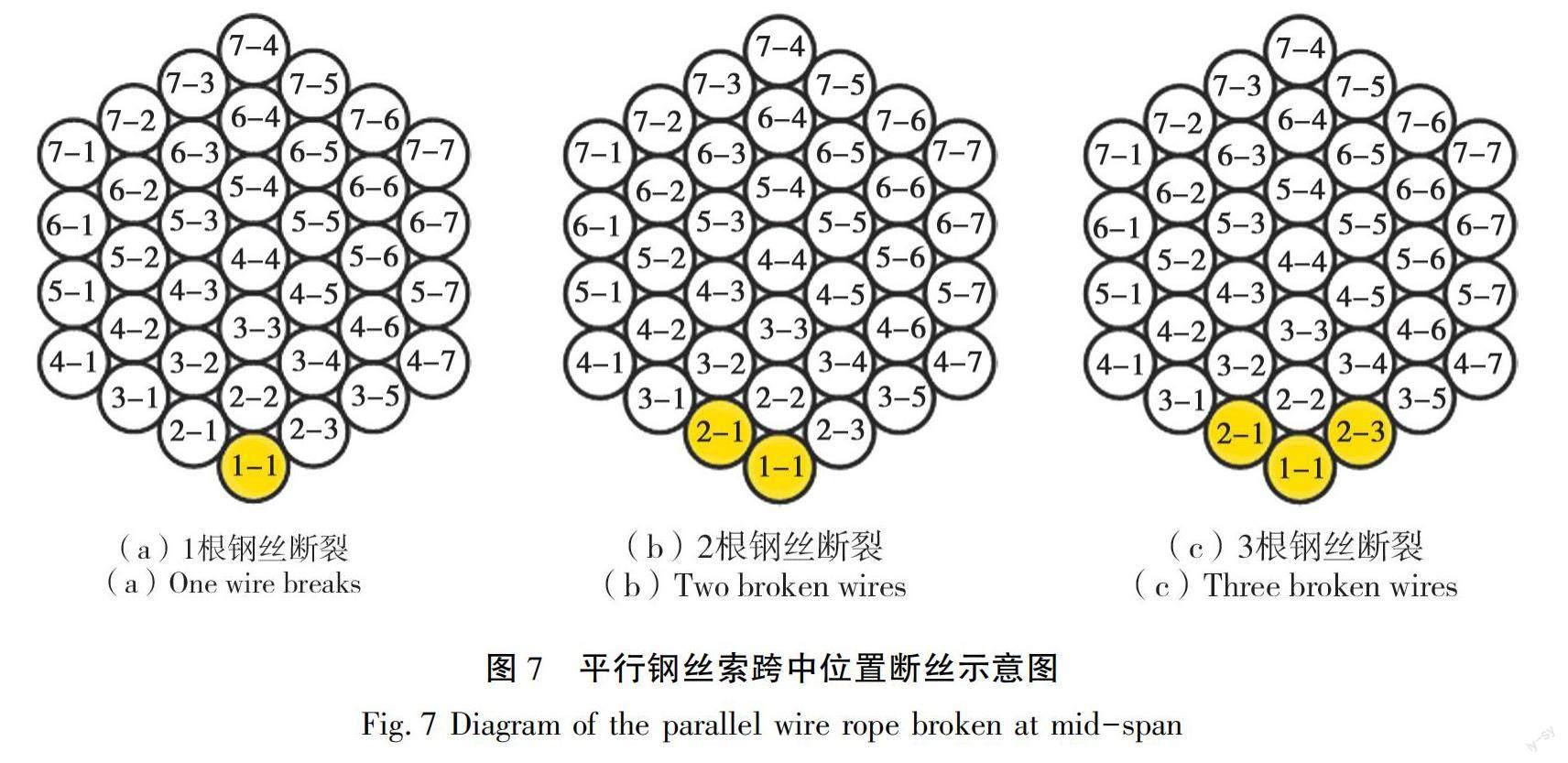
当平行钢丝索护套开裂后,在外层的钢丝最先发生锈蚀,蚀坑处会发生应力集中,产生相较于完好位置更大的应力,导致锈蚀最严重位置处最容易发生断裂。最外层钢丝受应力最大且跨中位置处产生的应力相对较大,故本研究分析37 φ7平行钢丝索在最不利跨中位置断一丝、两丝和三丝后对其他钢丝受力影响,断丝示意图如图7所示。
2.2.2 断丝有限元模拟
基于验证的平行钢丝索弯曲有限元模型进行钢丝断丝模拟,可清晰地对比断丝前后平行钢丝索的弯曲力学性能变化,在钢丝索跨中位置处利用ANSYS单元生死功能实现1-1钢丝断裂的模拟,即在计算之前选取单元,在一定拉伸荷载作用下“杀死”所选中的单元,被杀死的单元对结构的刚度矩阵不再具有贡献,生死单元法适用于大多数静态和非线性分析中。被“杀死”的单元会导致钢丝不再承受轴向荷载,但是由于平行钢丝索的几何特点,未断丝的区域仍然会存在接触,因而在后续计算中,仍然考虑断丝钢丝的接触刚度及钢丝间摩擦。
2.3 断丝后拉完耦合作用下变形分析
已有文献研究发现,平行钢丝索弯曲过程中X方向变形和Z方向变形幅度有限,且整索最大变形与跨中位置最大变形接近,故本节主要研究37 φ7平行钢丝索断丝后对跨中截面处整体变形的影响。对断一根钢丝的平行钢丝索在两端、自由、两端焊接和预拉力下弯曲变形进行分析,变形示意图如图8所示。
为研究37 φ7平行钢丝索1-1钢丝跨中位置断丝后对其他钢丝索跨中位置变形影响,对不同边界条件下平行钢丝索断丝后,1/3跨度处受到20 mm位移荷载时钢丝索内部钢丝相较于未断丝时变形程度(最大值)进行分析,其中变形量增大为+,变形量减小为-,结果见表3。
由表3可以看出,当1-1钢丝断裂后,3种边界条件下的37 φ7平行钢丝索内钢丝跨中截面变形均发生不同程度的增大,未出现减小现象,37 φ7平行钢丝索1-1钢丝断丝后内部钢丝变形均发生不同程度的增大,其中预拉力下的变形变化程度最大、两端焊接次之,对两端自由时的影响最小,但增大程度并不是对称的,这是因为当平行钢丝索受到弯曲荷载发生变形时,内部钢丝发生滑移错动是不规律的,1-1钢丝变形程度明显最大,这是1-1钢丝跨中位置发生断丝后,断丝位置更容易发生变形。两端自由时、两端焊接时和施加预拉力时,1-1#钢丝断丝截面处变形的变化程度都是最大的,分别增加3.41%、5.21%和5.35%。
2.4 断丝后仅有预拉力情况下应力分析
预拉力平行钢丝索断丝后断丝截面会出现应力重分布现象,主要与钢丝间产生的附加拉力和钢丝间摩擦力有关。为了研究断丝后平行钢丝索内部的应力重分布状况,考虑钢丝间联合工作模式以及平行钢丝索内部钢丝接触应力的分布状况。37 φ7平行钢丝索有4层钢丝,除最外层钢丝外,每根钢丝周围都均匀的分布着6根完整钢丝,并且均与相邻的钢丝之间存在接触挤压作用。对于其中任意一根钢丝,在平行钢丝索受到拉力的作用下,接触应力不仅受到其自身截面泊松收缩作用的影响,同时也会受到来自外层钢丝接触挤压的累积作用。为了分析平行钢丝索施加不同预拉力后,断裂不同数目钢丝对其他钢丝等效应力的影响规律,对平行钢丝索分别施加25、50、100 kN预拉力后进行断丝截面应力分析。
2.4.1 断裂1丝应力分析
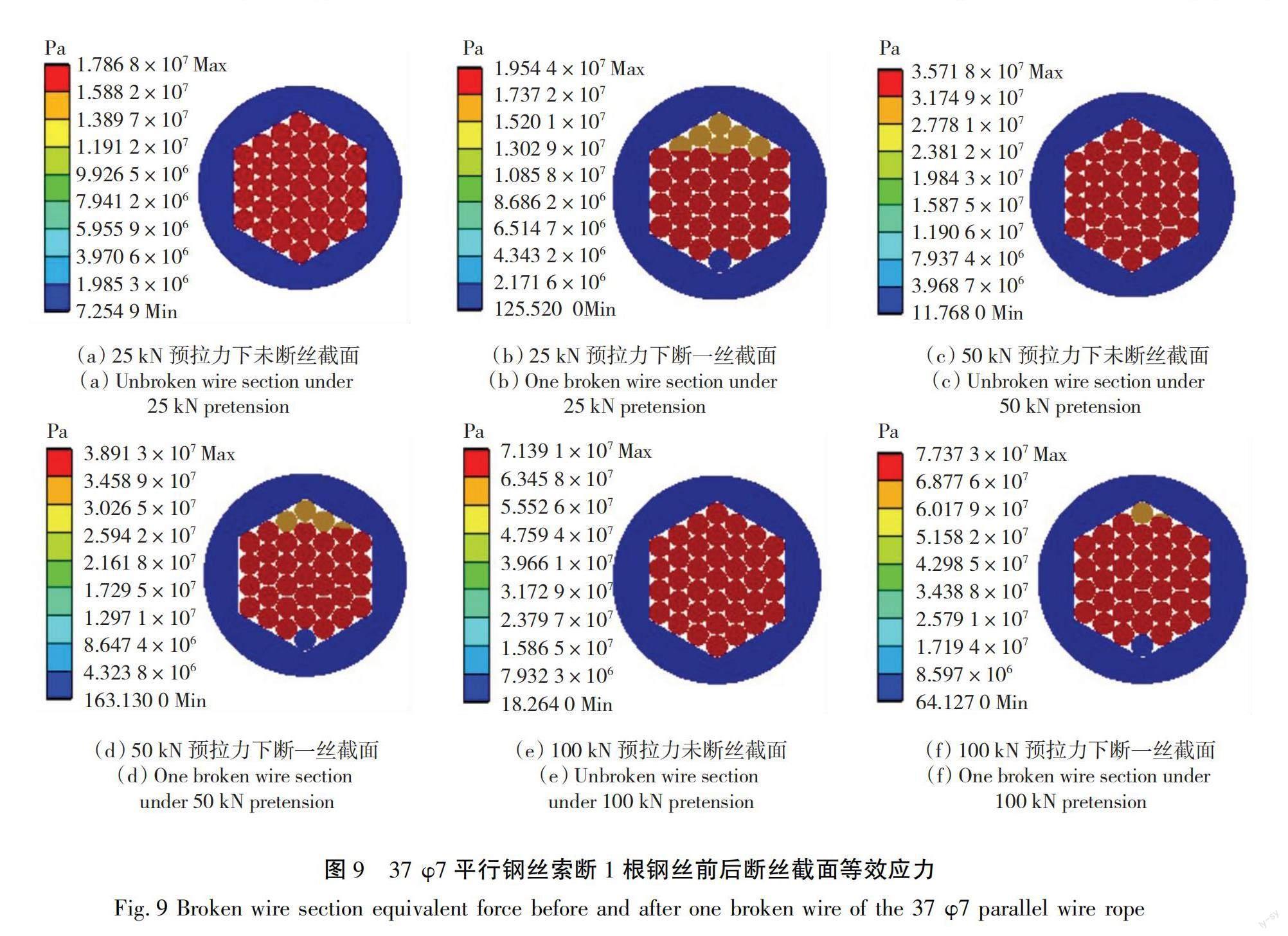
图9为不同预拉力下平行钢丝索跨中截面未断丝和断1根钢丝时,断丝截面钢丝的应力分布情况。
由图9可知,在3种预拉力情况下,未发生断丝时,跨中截面所有钢丝应力分布均匀,当1-1钢丝断丝后,平行钢丝索内部钢丝断丝截面均发生了应力重分布情况。1-1钢丝断丝位置处应力变化最为明显,产生应力很小,而距断丝位置最远的钢丝相较于其他完好钢丝应力最小,随着预拉力的增加,断丝后剩余钢丝的最大应力增加程度也更高。平行钢丝索内剩余钢丝的应力重分布由接触摩擦作用和附加弯矩作用共同决定,并且断丝处恢复长度内失去钢丝轴力所造成的附加弯矩为主要影响因素。为进一步研究平行钢丝索发生断丝后索内应力重分布,通过计算绘制断丝截面钢丝应力分布如图10所示。
由图10可知,3种预拉力情况下断丝截面应力重分布规律相似,当1-1钢丝断裂后,2-1钢丝和2-3#钢丝应力最大,7-4钢丝应力最小,即靠近断丝处的钢丝应力重分布后应力最大,距断丝处最远端钢丝应力重分布后应力最小。每组钢丝中,两端钢丝应力明显高于中间钢丝应力,且应力大小情况关于中间钢丝对称,表明在同一组钢丝中,以断丝处为原点,轴向钢丝应力高于径向钢丝应力。施加25、50、100 kN预拉力时,断丝截面剩余钢丝最大应力分别为19.54、38.91、77.37 MPa,相较于未断丝时分别增大11.18%、10.81%、10.16%。结果表明预拉力越大,断丝截面剩余钢丝最大应力相较于未断丝时增大幅度越小。
2.4.2 断裂2丝应力分析
当1-1钢丝断裂后,2-1钢丝和2-3钢丝在断丝截面应力最大,故模拟断裂2根钢丝时,选择2-1钢丝断裂。图11和图12为平行钢丝索断裂2根钢丝后在不同预拉力作用下,断丝截面的应力情况和断丝截面剩余钢丝应力分布图。
由图12可知,2根钢丝发生断裂后,同样会发生应力重分布现象,断裂的2根钢丝在断裂位置产生的应力很小,断裂钢丝周围钢丝应力高于远端钢丝且随着预拉力的增大这种现象更明显。由图11可以看出,1-1#鋼丝和2-1#钢丝断裂后,断丝截面剩余钢丝中2-3#钢丝应力最大,3-1#钢丝应力增大明显,同组钢丝中两端钢丝应力高于中间钢丝应力,但不再对称,小编#钢丝应力相对更高,由于2-1#钢丝断裂后,断丝是不对称的,2-1#钢丝周围剩余钢丝应力重分布后应力更大。施加25、50、100 kN预拉力时,断丝截面剩余钢丝最大应力分别为21.53、42.65、84.16 MPa,相较于未断丝时分别增大21.59%、20.63%、19.01%。随着预拉力增大,断丝截面剩余钢丝最大应力增大幅度越小。
2.4.2 断裂3丝应力分析
图13和图14为不同预拉力下断3根钢丝时,断丝截面的应力情况和断丝截面剩余钢丝应力分布图。
由图13和图14可知,断裂3根钢丝后应力重分布现象更加明显,当1-1钢丝、2-1钢丝和2-3钢丝断裂后,剩余钢丝中第3组两端钢丝应力最大与2-2钢丝应力接近,每组钢丝应力大小关于中间钢丝对称,这是因为3根钢丝是对称断裂的。施加25、50、100 kN预拉力时,断丝截面剩余钢丝最大应力为23.31、46.06、90.28 MPa,相较于未断丝时分别增大31.35%、30.29%、27.68%,变化趋势与断一丝和断两丝时相同。
从以上研究可以看出,在仅施加预拉力时,发生断丝时剩余钢丝就会出现应力重分布现象,越靠近断丝位置的剩余钢丝应力越大,随着断丝数量的增加,剩余钢丝最大应力也增加。在25 kN预拉力情况下,当断裂3根钢丝时钢丝最大应力增大31.35%,表明断丝数量越多,剩余钢丝受力状态越危险。
3 结论
1)平行钢丝索在两端自由、两端焊接和施加25 kN预拉力情况下,在1/3跨度处施加位移荷载时,平行钢丝索荷载-位移曲线均呈双折线形且初期斜率较大,预拉力平行钢丝索弯曲承载能力明显高于无预拉力平行钢丝索,焊接和预拉力都会提升平行钢丝索的抗弯刚度,且预拉力作用提升更明显。
2)断丝后无预拉力平行钢丝索弯曲变形无明显变化,预拉力平行钢丝索彎曲变形增大明显,最大变形发生在断丝处,增大5.35%。
3)对断丝平行钢丝索分别施加25、50、100 kN预拉力,跨中截面发生断丝时,剩余完好钢丝应力发生重分布,靠近断丝位置的剩余钢丝应力最大,远端钢丝应力最小,随着断丝数量的增加,剩余钢丝最大应力增加明显,在预拉力为25 kN时增大程度最明显,断裂1根钢丝应力增大11.18%,断裂2丝增大21.59%,断裂3丝增大31.35%。
4)无预拉力和预拉力平行钢丝索断丝后弯曲最大应力随着断丝数量的增加而增大,预拉力平行钢丝索钢丝应力增大明显,断丝位置应力很小,但距断裂位置一定长度时断裂钢丝应力会恢复。
【参 考 文 献】
[1]陈宝春,钢管混凝土拱桥.第三版[M].北京:人民交通出版社,2016.
CHEN B C. Steel-tube concrete arch bridges. Third Edition[M]. Beijing: People's Transportation Press, 2016.
[2]FENG M R. Modern bridges in China[J]. Structure and Infrastructure Engineering, 2014, 10(4): 429-442.
[3]郑罡,王鹏,唐光武.桥梁索结构[M].北京:人民交通出版社,2015.
ZHENG G, WANG P, TANG G W. Bridge cable structures[M]. Beijing: People's Transportation Press, 2015.
[4]徐腾.不同吊杆形式下系杆拱组合体系的受力性能和吊杆失效分析[C].西安:长安大学,2020.
XU Teng. Force performance and boom failure analysis of combined system of tied arch with different boom forms [C]. Xi'an: Chang'an University, 2020.
[5]平南三桥:引领拱桥建设新高度打造世界桥梁新名片[J].西部交通科技,2020(11):2-3.
Pingnan third bridge: leading arch bridge construction to a new height and creating a new business card for world bridges[J]. Western China Communications Science & Technology, 2020(11): 2-3.
[6]张秀成,谢奎,任毅勇.浅析“宜宾市小南门金沙江大桥”桥塌原因与修缮方案[J].河南城建高等专科学校学报,2002,11(2):15-17.
ZHANG X C, XIE K, REN Y Y. Analyzing the reason and renovating project of “little south door Jinsha River bridge of Yibin City” collapsing[J]. Journal of Henan Urban Construction Junior College, 2002, 11(2): 15-17.
[7]陈祥华.武夷山公馆大桥垮塌生命大营救[J].安全与健康,2011(16):9.
CHEN X H. Life rescue of Wuyishan Mansion Bridge collapse[J]. Safety & Health, 2011(16): 9.
[8]赵洪平,李元兵.拱桥吊杆损伤退化机理及寿命评估研究进展[J].城市道桥与防洪,2010(1):119-124,12.
ZHAO H P, LI Y B. Study on damage degenerating mechanism and life evaluation of arched bridge suspender[J]. Urban Roads Bridges & Flood Control, 2010(1): 119-124, 12.
[9]柏伟.在役平行钢丝斜拉索剩余寿命分析[D].重庆:重庆交通大学,2020.
BAI W. Residual life analysis of parallel wire cable in service[D]. Chongqing: Chongqing Jiaotong University, 2020.
[10]吴志杰,丁政,孙传平,等.钢绞线截面应力及破坏模式的有限元分析[J].中国科技论文,2018,13(22):2623-2628.
WU Z J, DING Z, SUN C P, et al. Finite element analysis of section stress and failure mode of steel strand[J]. China Sciencepaper, 2018, 13(22): 2623-2628.
[11]张杰.钢绞线拉索断丝效应分析及安全评估[D].西安:长安大学,2021.
ZHANG J. Analysis of broken wire effect and safety evaluation of steel strand cable[D]. Xi'an: Chang'an University, 2021.
[12]MONTOYA A, DEODATIS G, BETTI R. Physics based stochastic model to determine the failure load of suspension bridge main cables[J]. ASCE Computing in Civil Engineering, 2015, 29(4): B4014002.
[13]MALJAARS J, VROUWENVELDER T. Fatigue failure analysis of stay cables with initial defects: Ewijk bridge case study[J]. Structural Safety, 2014, 51: 47-56.
[14]KAEANCI E, BETTI R. Modeling Corrosion in Suspension Bridge Main Cables. I: Annual Corrosion Rate[J]. Journal of Bridge Engineering, 2018, 23(6): 04018025.1-04018025.15.
[15]MILONE A, LANDOLFO R, BERTO F. Methodologies for the fatigue assessment of corroded wire ropes: a state-of-the-art review[J]. Structures, 2022, 37: 787-794.
[16]权鑫鑫.平行钢丝束的弯曲性能研究[D].天津:天津大学,2019.
QUAN X X. Research on bending behavior of parallel steel wire cable[D]. Tianjin: Tianjin University, 2019.
[17]刘发,岳红宇,谢民滇,等.腐蚀斜拉索承载力退化模型研究[J].现代交通技术,2017,14(3):30-34,61.
LIU F, YUE H Y, XIE M D, et al. Research on degradation model of bearing capacity of corroded stay cables[J]. Modern Transportation Technology, 2017, 14(3): 30-34, 61.
[18]陈冠.多部件非均匀锈蚀对钢混组合梁承载力退化的影响研究[J].公路工程,2022,47(3):35-42,130.
CHEN G. Study on the effect of multi-component non-uniform corrosion on bearing capacity degradation of steel-concrete composite beams[J]. Highway Engineering, 2022, 47(3): 35-42, 130.
[19]朱萬旭,刘丰荣,朱世聪,等.钢绞线拉索疲劳性能优化试验研究[J].世界桥梁,2020,48(5):46-50.
ZHU W X, LIU F R, ZHU S C, et al. Experimental study of fatigue performance optimization for steel strand cables[J]. World Bridges, 2020, 48(5): 46-50.

