基于集合经验模态分解和优化支持向量机的风速预测模型
闫 帆,李傲燃
(云南大学,昆明 650504)
0 引 言
电力系统规划调整的具体过程将通过实时检测、数据综合分析、反馈决策及决策优化4个部分来实现,其中风速的准确预测是电厂提高效益并扩大规模的关键。虽然国内已做过大量有关风力预测的研究并提出大量模型,如数值天气预报预测法、统计回归预测法等,但基于风速的间歇性、波动性和不确定性,以上方法都有一定缺点。如数值天气预报预测法[2]需要大量天气环境数据;单一的统计回归预测模型[3]存在低阶模型精确度低、高阶模型结构复杂、需要繁重的运算资源等缺点[4]。
该文通过将风速原始数据输入模型,以分解时间序列,优化机器学习预测算法为解决思路,建立预测误差较小的风速预测模型。针对风速时间序列不确定性和单一预测模型预测精度不高的问题,提出了以经验模态分解(empirical mode decomposition, EMD)改进算法为基础的分解算法进行风速预测的思路,即通过集合经验模态分解(ensemble empirical mode decomposition, EEMD)对时间序列进行分解,建立优化粒子群优化算法(particle swarm optimization, PSO)优化支持向量机(support vector machine,SVM)模型组合预测算法,将各模态分量预测值叠加与重构得到预测结果。将预测结果与传统预测模型进行预测效果的比较,并进行定量误差分析。
1 算法理论
1.1 集合经验模态分解
为深入分析非平稳时间序列数据的局部频率特征,N. E. Huang等基于瞬时频率概念提出一种自适应非线性信号去噪技术——经验模态分解算法[5]。该方法的核心是将原始信号分解成一组振荡模式的单个分量信号,即固有模态函数(intrinsic mode function,IMF),这一分解过程可以得到平稳的、线性的IMF。
经验模态分解的核心是筛选固有模态函数,而对于非平稳数据,EMD分解也存在缺陷,主要原因是容易出现模态混叠。模态混叠是指一个IMF分量中包含差异极大的特征时间尺度。EEMD是一种基于噪声辅助分析的集合经验模态分解,可以消除模态混叠现象[6-8]。集合经验模态分解的步骤如下:
1)将标准正态分布的白噪声n(t)加到原信号,得到信号X(t):
X(t)=x(t)+n(t)
(1)
2)对加入白噪声的信号Xi(t)进行经验模态分解,得到j个IMF分量:
(2)
式中:Xi(t)表示第i次附加白噪声所得信号;ci,j(t)是第i次试验的第j个IMF;ri,j(t)为余项。
3)重复步骤1)、2)M次,通过加入不同正态分布的白噪声ni(t)得到IMF集合。
小麦新品种展示示范安排在我区东关街道办五一村大田中,前茬作物为玉米,该地地势平坦,灌溉方便,肥力中等。
4)将上述得到的IMF进行集成平均运算得到最终结果:
(3)
1.2 支持向量机
支持向量机(support vector machine, SVM)是一种基于二分类算法思想和监督决策思想的机器学习算法,用于寻找根据坐标特性分割二维数据点的理想直线,该直线在进行清晰划分的同时具有较强的鲁棒性和泛化能力。相比逻辑回归等方式,支持向量机提供一种更优的分类方式。而当待处理的数据集是三维及高维时,该数据不具有线性可分性,因此希望通过加入相关参数将数据输入高维空间,使数据集变成线性可分的形式,这个过程是由引入松弛变量和非线性映射实现的。在这个高维空间中,通过寻找超平面以进行最优分类:
(4)
r为样本到超平面的距离,在超平面中,w取(w1,w2),x取(x1,x2),可以将超平面写成直角坐标中直线y-y0=k(x-x0)的类似形式。w为平面法向量,b为平面与原点的距离。
1.3 粒子群算法和参数优化
粒子群算法是一种以鸟类捕食行为为原理的随机搜索算法[10]。在迭代进行时,粒子具有一个速度值以决定前进方向和距离,同时通过参考个体极值(ibest)和群体极值(gbest)更新相关参数。计算机实现模拟捕食的第一步是初始化粒子群位置、速度、gbest和ibest,迭代时不断更新ibest和gbest,当gbest符合要求时结束,反之继续进行更新。
为找到支持向量机模型中合适的参数以提高分类性能和泛化能力,该文尝试使用PSO优化SVM的参数。该优化方法基于交叉验证优化,交叉验证的思想是将训练样本分类,分别用于模型的预测和评估,再选择性能较好的样本作为模型,以达到评估和选择模型的效果。选择对其进行十倍交叉验证,并将均值作为算法精度的估计。
2 实例风速预测与分析
2.1 数据集选取
以中国北方某风电场2020年1月1日0时至12月23日24时,采样间隔为5 min的全年风速数据为实例进行风速预测与分析。考虑到时间跨度和采样间隔造成的影响,为减小试验干扰并保证结论普适性,选取2月1日0时至3月6日6时内,采样间隔为1 h的数据集共800组。其训练数据数量的选取约为样本数量的80%,剩余测试数据在时序上体现为训练数据的延拓。
2.2 预测效果评估及指标
采用误差分析的不同模型对预测效果进行分析和评估,使用到的分析模型包括均方根误差(root mean squared error, RMSE)、平均绝对误差(mean absolute error, MAE)和决定系数r2等。
2.3 数据预处理
将风速原始序列进行EMD分解,根据不同尺度或趋势分量进行逐级分解得到7个相互独立的IMF分量和余项res,分解结果如图1所示。

图1 EMD分解结果及分量对应频谱图
观察EMD分解得到的各分量,IMF2与IMF3包含差异较小的特征时间尺度。为克服较严重的模态混叠现象,通过配置0.2白噪声、集合次数100的EEMD分解,得到8个IMF分量,如图2所示。观察分解结果可以看到,在EEMD分解结果中,不同分量的时间尺度差距更加明显。
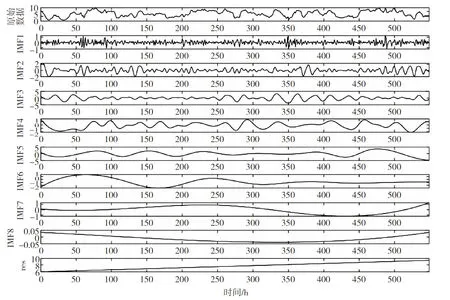
图2 EEMD分解结果及分量对应频谱图
2.4 EEMD-PSO-SVM组合预测
由于风速的间歇性与波动性,采用单一的预测方法难以取得较好的预测结果,提出一种EEMD-PSO-SVM组合预测模型。根据不同尺度、特征的趋势分量,分别使用PSO对粒子样本进行学习训练,自适应选择最优参数,得到各分量对应SVM模型中的c和p,c、p分别为惩罚系数、核函数参数。对上文所得模态分解结果进行归一化,再将分量输入模型得到预测结果。分别计算平均绝对误差MAE和决定系数r2,得到各IMF预测模型的参数及误差评估结果,如表1所示,其中cbest和pbest分别为最佳惩罚系数和最佳核半径。

表1 PSO-SVM模型参数表
为验证EEMD-PSO-SVM组合预测模型的优越性,将原始序列及EEMD分解序列分别输入向量机预测模型进行对比试验,得到SVM、EEMD-SVM模型风速预测结果。其中对EEMD-SVM模型进行定量精确度评估,得到模态分量预测参数及精度表,如表2所示。

表2 模态分量预测参数及精度表
最后将预测结果进行反归一化和重构,将225个测试样本的前70例数据预测结果与原始序列进行比较。图3反映了分别使用EEMD-PSO-SVM,EEMD-SVM,SVM这3种模型分别进行1 h风速预测的结果(局部)和误差分布情况。
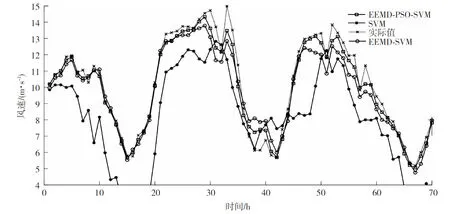
图3 不同模型预测结果对比(局部)
对于预测结果需要进行定量分析,结合不同模型的预测结果,分别使用均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)进行计算,3种模型的误差指标如表3所示。
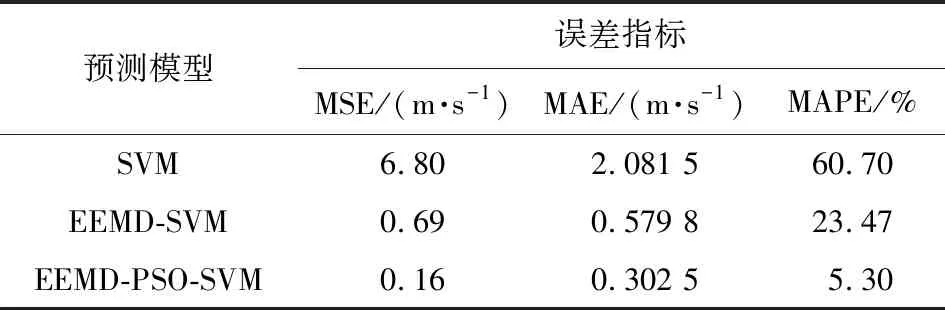
表3 不同模型的预测精度表
图3和表3给出了不同预测模型的预测结果和统计误差指标。可看出,该文提出的方法的预测曲线拟合程度较好、误差较小。相比SVM模型,EEMD-SVM模型在引入模态分解的同时大幅提升了预测曲线与原序列的拟合度,避免了不同频率尺度的相互干扰,体现了模态分解在处理非平稳序列的优越性。EEMD-PSO-SVM模型在上述基础上优化了向量机惩罚参数和核函数参数的选取,这是因为PSO具有的全局搜索特性使向量机具有合适的学习能力和较强的泛化能力,同时也减小了处理部分数据时陷入局部最优的可能性。
结合图3和表3,对比传统单一预测模型和EEMD-SVM模型,后者的统计误差指标相比单一预测模型分别降低6.11 m/s、1.50 m/s和37.23%,而对比EEMD-SVM模型和EMD-PSO-SVM模型,后者的平均绝对误差和平均绝对百分比误差相比前者分别降低0.28 m/s和18.17%。
对于风速序列中的极值点和发生较大波动的数据点,提出的组合预测模型相较于传统预测模型有更好的拟合效果,相关误差指标均显著降低,这也表明结合EEMD预处理和PSO优化支持向量机能够有效提高模型可靠性,实现较高精度的短期精度预测。
3 结 语
基于风速的波动性和间歇性,提出了EEMD-PSO-SVM组合预测模型。该预测模型将原始序列分解为具有不同尺度的IMF分量,分别建立PSO-SVM预测模型,优化得到最佳向量机参数,从而建立对应的最优预测模型。该组合预测模型实现了在保证精度和可靠性的同时避免复杂的模型结构。
通过对实例数据进行预测,对比传统单一预测模型与该文提出的EEMD-PSO-SVM组合预测模型,改进模型的MAE、MAPE等统计误差指标大幅度降低,预测精度能更好地满足工业和生产需要,具有较强可行性和工程应用价值。

