统计建模中GeoGebra软件的应用

张唯一

摘要： 用统计软件处理数据已成为统计学习的必要组成部分。统计图的绘制和统计量的计算是统计建模难点。以高中数学一元线性回归建模为例，教师设置定量探究不同因素对PM2.5浓度的影响这一问题情境，利用数学教学软件GeoGebra，指导学生绘制散点图，计算回归方程，对回归模型拟合并作效果评估，不仅能将学生从制图和计算中解放出来，高效开展建模活动，而且有利于调动学生在实际中使用统计方法的积极性。

关键词：一元线性回归模型；散点图；GeoGebra；统计建模

统计学是采用收集数据、分析数据等手段来认识未知现象的一门科学。用统计方法解决实际问题，必然涉及数据处理问题。当数据量大时，纯粹依靠纸笔计算，数据处理的工作量是非常大的，以致很多统计方法难以应用。随着计算机技术的发展，各种专业统计软件被开发出来，处理大量数据不再困难，这大大促进了统计方法的应用和统计学的发展。当今，用统计软件处理数据已成为统计学习的必要组成部分。在高中数学课程中，《普通高中数学课程标准（2017年版）》对统计中使用信息技术提出要求 ：对于必修课程的一维数据，“可以鼓励学生尽可能运用计算器、计算机进行模拟活动，处理数据”；对于选择性必修课程的成对数据，明确要求“会使用统计软件进行数据分析”。

如何根据随机性数据推断变量之间关系？建立统计模型是解决这类问题的常用方法。开展有效的统计建模活动，是应用统计知识解决实际问题的必经过程。在解决实际问题的过程中数据处理量较大，学生学会借助信息技术工具处理数据对于高效建模非常重要。下面结合人教A版《普通高中教科书数学选择性必修第三册》“建立统计模型进行预测”中，定量探究不同因素对PM2.5浓度的影响这个案例，介绍在回归分析中建模的过程与方法，以及信息技术的应用要领。此案例收集了24个监测点汽车流量、平均气温、空气湿度、风速、PM2.5浓度等数据，因为不影响后续行文，这里不再呈现。教科书采用的信息技术是R语言，借助编程实现统计计算和统计制图。为了降低使用信息技术的难度，这里采用操作相对容易的数学教学软件GeoGebra（以下简称“GGB软件”）。

一、利用散点图观察变量之间的关系

显然探究不同因素对PM2.5浓度的影响，是一个研究变量之间关系的问题。为了初步了解数据分布的特征，对数据进行可视化表示是统计中常用且有效的手段。对数据进行可视化表示，不仅可以直观判断变量之间的关系，而且可以为后续进一步开展定量研究提供思路和方向上的指引。学生利用软件画图不仅速度快，省时、省力，而且标准、美观，有利于更好地观察数据的特征。

为了简单起见，我们研究PM2.5浓度与汽车流量两个变量之间的关系。首先判断两个变量有没有关系，若有关系是什么关系。观察两个定量变量的成对观测数据分布特征，最常用的是散点图。散点图的绘制可以由GGB软件完成。学生将PM2.5浓度与汽车流量数据输入软件的表格区（见表1），选中两列数据（B2：C25），点击工具栏中“双变量回归分析”，即可得到以汽车流量为横轴、PM2.5浓度为纵轴的散点图（如图1）。

如何利用散点分布的特征寻找两个变量之间关系？观察散点图，可以发现：PM2.5浓度随汽车流量的增加呈增长趋势，但汽车流量增加对应的PM2.5浓度并不一定增加，甚至还有个别汽车流量相同而对应的PM2.5浓度不同的情况。由此判断两个变量不是函数关系，而是相关关系。

二、借助一元线性回归模型刻画变量之间的关系

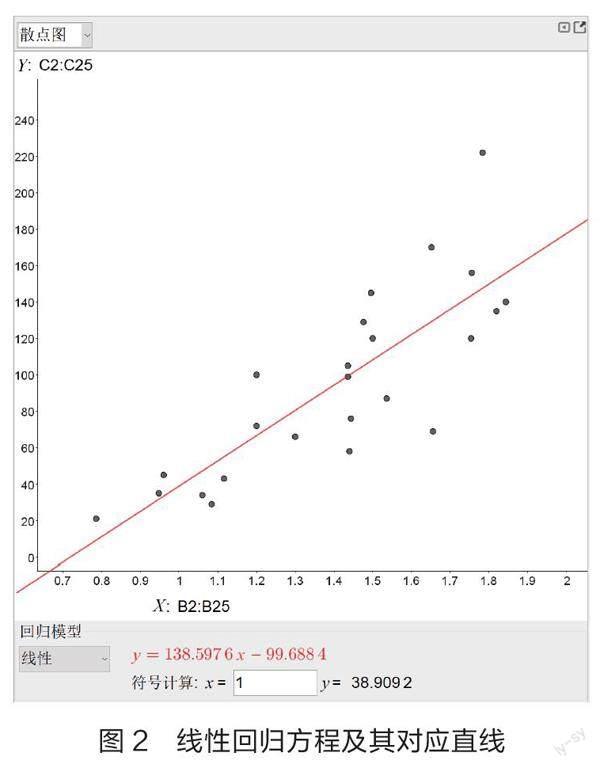
可以看到，参数估计的计算量较大，当数据量大时更是如此。利用GGB软件计算时，只需要操作鼠标，就可以得到回归方程并进行预测。软件计算不仅速度快，而且准确度高。

在图1界面的左下角，选择回归模型为“线性”，可得到回归方程y=138.597 6x-99.688 4，以及其对应的直线（如图2）。学生根据此回归方程进行预测：只要在左下角空白框中输入汽车流量的值，就可得到对应的平均PM2.5浓度。

三、对模型的拟合效果进行评估

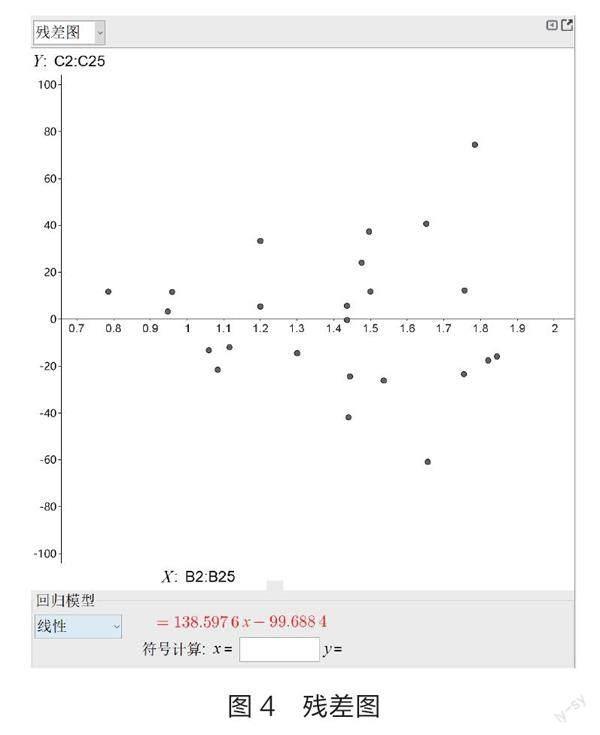
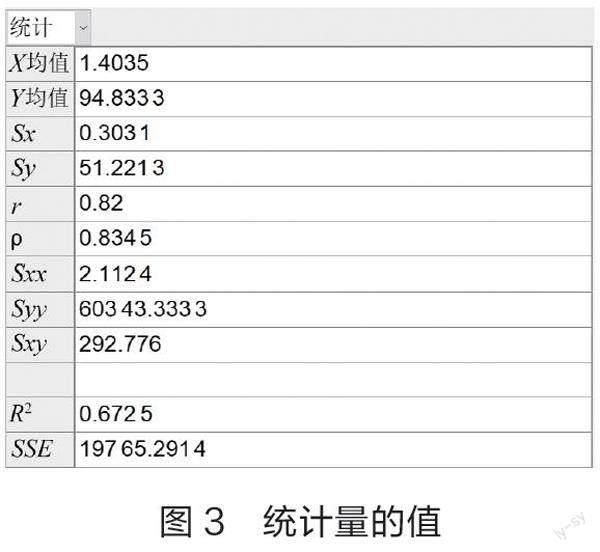
评估模型的拟合效果，是统计建模的重要环节。在高中，模型的拟合效果主要是根据R²的大小和残差图散点的分布进行评估。相关计算和绘图可以由GGB软件完成。

对于上述一元线性回归模型的拟合效果，在图2界面中，左上角点击“∑x”（显示统计），可得到R²为0.672 5（如图3）；在左上角选择“残差图”，可得到残差图（如图4）。由R²可知模型拟合的效果一般，还有改进的空间。观察残差图发现，残差在汽车流量不同取值时不是一个常数，而是随着汽车流量的增加而增加，这说明回归模型中对于随机误差的方差假定（D（e）=σ²）不合理。

虽然学生在高中阶段只学习一元线性回归模型，但利用GGB软件，还可以尝试用不同的回归模型拟合数据。只要在图2界面的左下角，选择其他类型的回归模型，如“对数”“多项式”“幂”等，就可以快捷得到不同的经验方程的曲线，以及R²和残差图。学生可以比较不同模型的R²和残差图，将拟合效果相对好的作为最終选择的回归模型。

上述案例证明，在信息技术辅助下作回归分析，学生可以完整参与统计建模活动。从数据直观表示到建立模型再到预测，中学涉及的所有建模过程都可以在GGB软件中完成，这个过程在统计建模中具有一般性。事实上，各种统计方法在统计软件中都可以找到相应的实现功能。从应用统计方法角度看，重要的是数据分析的思路，学生要学会选用合适的统计方法，并对统计的结果作合理的解释，而统计制图和统计计算工作可以交给统计软件完成。

在高中数学统计建模活动中，教师合理使用统计软件对教学大有裨益：不仅将学生从机械、烦琐的数据处理中解放出来，专注于寻找数据分析思路、选择统计方法、解释结果等创造性工作，使活动顺利开展，而且降低实际问题中使用统计方法的难度，提高其主动使用统计方法解决实际问题的积极性。

（作者系人民教育出版社中学数学编辑室副主任、副编审）

责任编辑：祝元志