基于FCM 聚类模型约束的二维初至旅行时反演

刘佳成，张志勇*，周钦渊，李曼，李红立

（1. 东华理工大学地球物理与测控技术学院，江西南昌 330013；2. 湖南省交通规划勘察设计研究院有限公司，湖南长沙 410008；3. 广西科技大学，广西柳州 545006）

0 引言

地震旅行时成像是以地震波在不同介质中传播规律为基础，在地表或井中观测地震信号，通过旅行时反演重构地质体内部速度分布的一种地球物理勘探方法。该方法广泛应用于工程检测、油气勘察、地球内部结构研究等［1-3］。地震初至波旅行时成像能识别、追踪目标地质体，稳定性较好，对浅层成像精度较高。

地震旅行时成像的过程主要包括正演和反演两部分。早期的地震旅行时正演采用经典射线追踪方法，如打靶法［4］、高斯射线束法［5］、弯曲射线法［6］，但可能存在多条射线路径，反演极易出现多解。为此，后续发展了基于程函方程的地震旅行时算法，如有限差分算法［7］、快速推进算法（Fast Marching Method，FMM）［8］、最短路径算法［9］等。其中FMM 是一种网格数值算法，通过有限差分或有限元方法求解程函方程追踪地震波前界面，具有较高的精度和效率，因而被广泛应用［10］。由于地震资料观测的局限性、观测数据中存在误差等原因，地震旅行时反演是一个不适定问题，反演算法主要有阻尼最小二乘法［11］、基于正交分解的最小二乘法（LSQR）［12］、子空间反演法［13］、代数重建技术（ART）［14］等，这些算法在不同程度上能降低反演问题的不适定性。此外，正则化技术［15］通过引入地球物理先验信息减少了反问题的多解性、提高了解的稳定性，因此被广泛用于地球物理反演［16］。最小结构模型约束是将最小模型稳定泛函与最大光滑稳定泛函加入到正则化项中，可有效降低反演问题的不适定性，但地质体边界刻画模糊，尤其是对射线分布稀疏的地质体分辨率较低。

近年来，模糊C 均值（Fuzzy C-means，FCM） 聚类算法已用于地球物理反演［17-20］。该算法通过反复修改聚类中心及每个网格单元对聚类中心的隶属度，实现对反演结果的自动分类［17］。此外，通过将先验信息作为参考聚类中心的方式，将FCM 聚类算法从无监督学习变成监督学习，引导每个网格单元向先验信息的方向修正，可有效提高反演结果的精度［19-20］。

本文在地震初至波旅行时成像中，采用非结构三角形进行网格剖分，采用Sethian 等［8］提出的FMM 算法进行正演计算，在地震旅行时正演过程中直接计算灵敏度但不存储射线路径［16］。采用以模型灵敏度信息为依据的渐进反演网格优化技术［21-22］，在最小结构模型约束正则化反演基础上，引入FCM 聚类模型约束，实现了基于FCM 聚类模型约束的二维地震初至波旅行时渐进反演；对比了无监督学习与先验信息监督学习反演结果，并应用简单模型讨论了FCM 聚类模型约束的权重、先验信息引导项权重等参数选取策略；最后，通过实测数据的反演验证了方法的有效性和实用性。

1 方法原理

1.1 地震初至旅行时反演

在最小结构模型约束正则化技术［23］的基础上，引入FCM 聚类模型约束项，构建地震初至波旅行时反演的目标函数

式中：m为模型速度向量；φd（m）为初至波旅行时观测数据dobs与正演响应A（m）间的数据拟合项；φm（m）为模型拟合项；φFCM（m）为FCM 模型约束项；λ为正则化因子；β为FCM 聚类模型约束项的权重；Wm为模型误差矩阵；mref为参考模型向量；Wd为数据方差矩阵，形式为

式中：σi为的数据方差；N为观测的初至波旅行时数据个数；ζ为极小的正有理数，保证分母不为0。

本文采用最小结构稳定因子［24］作为模型拟合项

式中：αs为最小模型稳定泛函的比例系数；αx、αz分别为最大光滑稳定泛函在x和z方向的比例系数；∂m/∂x和∂m/∂z分别表示模型向量在x和z方向的偏导数；积分是对任意单元的面积分。

1.2 FCM 聚类模型约束

FCM 聚类算法的思想是在迭代过程中，反复修改聚类中心和聚类中心的隶属度，是一种无监督学习。FCM 聚类的优化目标函数为

式中：C为聚类中心个数；M为模型单元总数；mj为第j个模型单元速度；隶属度uj，l表示第j个模型单元属于第l个参考簇的程度；模糊化参数q控制隶属度uj，l模糊化程度，本文取q=2；vl为第l个簇中心的速度值。uj，l为非负数，满足

为了改善反演效果，将先验信息引入FCM 聚类目标函数φFCM（m）［17］，将聚类算法从无监督学习升级为监督学习，即

式中：tl为第l个参考聚类中心；κl为第l个参考聚类中心的权重因子。

φFCM（m）的第一项可表示为

式中

1.3 目标函数优化求解

本文反演采用高斯—牛顿法求解模型参数向量m。假设第n+1 次迭代，对正演算子A（m）做一阶泰勒展开，并将第n+1 次迭代目标函数φ（n+1）（m）对Δm（n）进行求导并取0，可得高斯—牛顿方程

式（9）可写为

采用稳定双共轭梯度法（BICGSTAB）［21］求解Δm(n)

再根据线性搜索步长更新模型参数

式中η为搜索步长，可表示为

式中ξ为极小的正实数，确保分母不为0。

1.4 基于模型灵敏度的自适应反演

本文采用变网格技术实现地震初至波旅行时反演。在反演的初期采用较粗的网格，通过减少单元数降低反演的多解性，再利用模型灵敏度信息进行自适应网格加密［22］。以上一轮反演结果作为网格细化后反演的初始和参考模型，确保反演的稳定性，同时改善反演效果。定义模型灵敏度为

式中Jij为灵敏度矩阵的元素。模型灵敏度Sj表示单元的模型参数mj改变时对全部观测数据集的影响。对于测点处单元的模型灵敏度较大，网格的细化会从测点逐渐向反演区域的深部进行，因此具有对反演区域整体优化的特点。基于模型灵敏度的自适应反演过程如下。

（1）读入观测数据，设置每重网格最大的迭代次数、最小单元面积、网格优化比例（为反演单元总数的2%）。

（2）从数据信息生成正演模型的几何描述，设置反演范围，并做非结构三角形网格剖分。

（3）对当前网格下使用BICGSTAB 最优化算法求解高斯—牛顿优化的反演目标函数，直至满足BICGSTAB 的迭代次数，并求取模型改变量。

（4）通过模型灵敏度网格优化方案计算单元模型灵敏度信息，按照网格优化比例选取需要细化的网格单元，进行网格的自适应加密。

（5）将上一轮反演结果作为细化后反演的初始和参考模型，并判断是否达到反演终止的条件。满足则终止反演，否则返回第三步开始网格细化后的反演。

1.5 参数选取

地震初至波旅行时反演的目标函数φ（m）中的正则化因子λ是平衡数据拟合项与模型拟合项的关键参数。本文采用李曼等［25］提出的改进“L 曲线”算法求取λ。该算法无需利用导数信息，可以自动舍弃错误的曲率点，能提高正则化因子的求取精度。

引入FCM 聚类模型约束的同时，也引入了聚类中心的个数C、参考聚类中心tl、参考聚类中心的权重因子κl、FCM 聚类模型约束项权重β等众多参数。这些参数势必会影响反演的稳定性及效果。因此如何选取合适参数是引入FCM 聚类模型约束反演的一个关键问题。其中，聚类中心的个数C及参考聚类中心tl可通过获取有效且精确的先验信息确定。参考聚类中心的权重因子κl的作用是引导聚类中心向真值靠近，FCM 聚类模型约束项权重β的作用是控制反演中FCM 聚类模型约束项的比重。为此，对κl和β参数不同组合的反演效果进行了对比分析，讨论了两个参数在反演过程中的作用；结合渐进反演网格优化技术的特点，提出了一种FCM 聚类模型约束参数的自动选取方案。该方案在选取一个适当的聚类中心权重因子κ=100 后，通过减少反演前期FCM 聚类模型约束比重，让正则化项占主导，后期增大FCM 聚类模型约束比重实现FCM 聚类模型约束。将每重网格的FCM 聚类模型约束项权重修改为

式中K为每重网格的迭代次数。

2 算例分析

2.1 模型算例1

为了验证算法的有效性，设计了图1 左所示的理论模型。在背景速度为2000 m/s的均匀半空间中，设计了两个尺寸为30 m×30 m 的高速异常体，速度均为3000 m/s，顶面埋深分别为10和90 m。

图1 异常体模型（左）及最小结构模型约束反演结果（右）

采用双井激发、井中和地面同时接收的观测系统。井中深度2.5 m 处开始设置炮点和检波器各60个，地表均匀布设60 个检波器，炮点距和检波点距都为2.5 m，井间距为120 m。基于上述参数进行地震初至旅行时正演，将理论旅行时加入5%的随机噪声作为观测数据（共14400个）。

反演的初始速度模型是速度为2000 m/s 的均匀半空间，初始正则化因子λ设置为10000。最小结构模型约束反演结果如图1 右所示，可以大致判断两个高速异常体的位置，浅部的异常体的规模和速度与实际值接近，但深部异常体规模较大，速度与实际值相差亦较大。

为了分析基于模型灵敏度渐进反演过程，对于图1右所示反演模型，设计了四重网格，第一重网格的迭代次数为5，其他的最大迭代次数为10，反演过程的网格变化如图2 所示，从测点处逐渐向反演区域内部细化。表1 给出了每重网格的反演单元个数、迭代次数及反演开始与结束的均方根误差（RMS）。单元数由1961 逐渐增加到3883；初始网格和第一次细化网格反演的RMS 下降很快，后两次的RMS 下降量减少并趋于稳定。

表1 渐进反演次数、RMS 统计

图2 多重网格细化示意图

首先根据精确的先验信息，设置了FCM 聚类模型约束反演的两个参考聚类中心：v=2000 和3000 m/s。其次，为分析参考聚类中心的权重因子κ（本文算例中不同参考聚类中心的权重因子设为相同）和FCM 聚类模型约束项的权重因子β对反演结果的影响，设置κ和β分别为1、10、100、1000、10000，对比不同参数组合的反演结果（图3）。

由图3可见：

（1）当聚类中心权重因子κ=1或10时，随β增大，反演结果的聚类特征更明显，但速度值较真值差异变大（图3的第1、第2行）。

（2）当FCM 聚类模型约束项权重β=1、10、100时，随聚类中心权重因子κ的增大，异常体的特征改善不明显，也没有明显的聚类特征（图3 的第1～第3 列）。原因是聚类中心权重因子κ较大时引导每个单元的速度向真实值靠近，但控制聚类程度的FCM 聚类模型约束项权重β较小，聚类效果不明显。

（3）适当的参数组合可以得到理想的反演结果，如κ=100、β=1000 或10000 时的反演结果异常体尺寸与真实模型接近（图3 第3 行的第4 和第5 列），而β=10000 时反演的异常体速度与真实更接近（图3第3行的第5列）。

（4）越大的κ和β组合的反演结果的聚类特征越明显（图3第5列的第4和第5行），但异常体的尺寸偏小。

由以上分析可知，适当的聚类中心权重因子κ能有效地引导聚类中心向真值靠近，而FCM 聚类模型约束项权重β可以控制聚类程度。因此，本文采用前文提出的FCM 聚类模型约束参数的选取方案，即通过减小反演前期FCM 聚类模型约束项比重β，让模型正则化项占主导，后期增大FCM 聚类模型约束项的权重实现FCM 模型约束。新参数选取方案的反演结果如图4所示，与未加入FCM 聚类模型约束的反演结果（图1 右）相比，背景更干净，两个高速异常体尺寸、位置及速度值与实际更吻合，边界刻画清晰。与图3第3行第5列的反演结果接近。

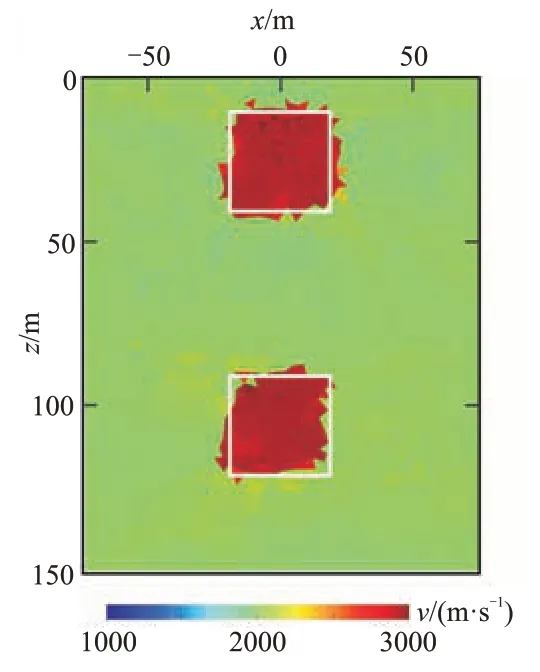
图4 新参数选取方案的FCM 聚类模型约束反演结果

为进一步分析FCM 聚类模型约束的地震初至波旅行时反演效果，对最小结构模型约束和加入FCM模型约束反演结果的速度频数进行统计（图5）。可见，FCM 聚类模型约束通过引入先验信息，反演结果中出现两个峰值与实际给定的两个聚类中心接近，形成了有效的聚类效果。

（4）该水源地远期应对措施应严格执行水功能区划的目标要求，通过流域协同治理，削减流域污染负荷；同时构建区域协同管理机制，实现信息共享。

图5 FCM 聚类模型约束引入前（左）、后（右）反演结果的速度频数统计直方图对比

2.2 模型算例2

为进一步验证基于FCM 聚类模型约束的地震初至波旅行时反演能提高成像分辨率，设计了如图6 左所示的层状模型，区域1、区域2 和区域3 是速度分别为1000、2000、3000 m/s 的均匀介质。采用与模型算例1相同的观测方法和参数进行正演计算。

图6 层状模型（左）与加入FCM 聚类模型约束前（中）、后（右）反演结果对比

反演的初始模型是速度为2000 m/s 的均匀半空间，初始正则化因子λ为10000，设置了v=1000、2000、3000 m/s 三个参考聚类中心；采用模型算例1中FCM 聚类模型约束参数的选取方案。

图6 中为最小结构模型约束的反演结果，可以大致判断层状速度带，但各层边界模糊，界面附近的速度值与实际相差较大；图6右为加入FCM 聚类模型约束的反演结果，与图6 中相比，能明显区分3 个区域的层状速度带，界面位置较准确，刻画清晰，速度值与真值更吻合。

图6 两种方法反演结果的速度频数统计如图7所示，加入FCM 聚类模型约束后，三个峰值的速度与引入的三个先验信息吻合，形成了有效的聚类特征。

图7 层状模型加入FCM 聚类模型约束前（左）、后（右）反演结果的速度频数统计直方图对比

2.3 实测数据反演

使用强风化层中的孤石（微风化或未风化的花岗岩）探测的井中地震初至波旅行时数据验证本文方法的有效性和实用性。实测数据由单井激发、单井接收观测系统采集。在孤石两侧各布置一个深度为20 m的钻孔，钻孔间距为9.4 m，共布置17 个炮点和36 个检波器，左侧从3.0 m 深度开始布设炮点，炮点距为1 m；右侧从深度2.5 m 开始布置检波器，道间距为0.5 m。共采集有效旅行时观测数据612个。

在测线5 m 处的验证钻孔揭示：0～2.6 m 为人工堆积黏性土；2.6～7.0 m 为坡积而成的粉质黏土；7.0～9.8 m 为花岗岩风化残积而成的砂质黏土；9.8～12.2 m为花岗岩微风化体（孤石）；12.2～16.5 m为花岗岩风化残积而成的砂质黏性土；16.5～33.6 m为全风化层，局部夹强风化花岗岩；稳定的潜水面深度为2.5 m。

图8 左为未加入FCM 聚类模型约束的反演速度剖面，可以大致判断孤石（高速异常体）位置，与钻孔信息吻合，但尺寸较小，且速度与背景差异不够明显。图8右为加入FCM 聚类模型约束后的反演速度剖面，为了凸显高速异常体的明显特征，设置了v=2000 和3000 m/s两个参考聚类中心，采用模型算例1中FCM聚类模型约束参数的选取方案。由图8右能清晰地判断孤石的位置及边界，异常体的尺寸和速度值都与实际钻孔信息吻合。

3 结束语

为了提高地震初至波旅行时对浅层结构的成像精度，本文提出了基于FCM 聚类模型约束的地震初至波旅行时反演方法。通过理论研究、模型数据和实测数据试算，取得以下几点认识：

（1）FCM 聚类模型约束易与传统正则化反演结合，可有效提高反演结果的分辨率；

（2）FCM 聚类模型约束通过引入精确的速度先验信息，可有效提高速度反演精度；

（3）FCM 聚类模型约束权重、先验信息引导项权重直接影响反演结果，本文的自动选择策略有效改善了反演效果，降低了参数选择难度。