基于深度神经网络的探地雷达杂波抑制和根参数预测方法

李光辉，马嘉辉，王哲旭，魏 槊

（江南大学人工智能与计算机学院，无锡 214122）

0 引言

根系在树木生长过程中扮演着重要角色，具有吸收水分、运输养分和固定植物体等功能。根系检测有助于了解植物生长、健康状况以及土壤中的物质循环[1-2]，传统方法（例如根钻法、土壤剖面法等）多为破坏性检测，有着操作复杂以及可能造成不可逆损伤的缺点。探地雷达作为一种无损检测工具，相对于其他无损检测技术（例如核磁共振法、电阻率层析成像和声学方法等[3-4]）具有携带方便、操作简单、成本低廉等优点，近年来已广泛应用于浅层地下物体检测，但是由于树木根系所处复杂环境导致数据的解译仍然面临挑战[5-6]。

探地雷达由发射天线和接收天线组成，在被检测地表以合成孔径的方式沿检测线平移，发射天线向地下发射特定频率的电磁波，而根系和周围土壤的相对介电常数分布，将导致接收天线接收到不同的反射电磁波信号。通过分析接收到的信号可以推测出地下根系的位置及根生物量等信息[7-9]。但是由于天线间的耦合、地面反射直达波、地下介质随机分布的复杂性等因素[10-11]，导致收集到的原始B-scan 数据中存在杂波，对目标信号的分析造成严重干扰，增加了地下根系的检测和特征提取的难度。崔喜红等[12]使用回归模型来建立雷达波形振幅强度、时间跨度和根系直径、生物量的统计关系，对于根直径大于0.005 m 的情况下，R2值达到0.85。随着深度神经网络的发展，许多学者将其应用于探地雷达数据解译，王泽鹏等[13]应用YOLOv3 强大的特征提取能力对根双曲线进行感兴趣区域划分，识别准确率和召回率分别达到了96.62%和86.94%，然后使用随机霍夫变换拟合双曲线，根系参数预测的总平均相对误差在10.57%以内。但目前对根参数的估计大多没有考虑雷达信号受复杂土壤环境的影响，将土壤视为均匀介质，使用双曲线拟合估计其平均介电常数，这导致检测算法在不同土壤环境时鲁棒性降低[14-16]。此外，探地雷达检测数据通常需要经过预处理、感兴趣区域框定、双曲线信息提取等多个处理阶段，容易导致误差累积。

针对以上问题，本文提出了一种针对异质土壤介质下的基于深度神经网络（deep neural networks,DNN）的探地雷达杂波抑制和根参数预测方法。该方法首先使用改进U-net 网络实现杂波抑制，从原始B-scan 图像中获取仅含有目标树根反射响应的纯净双曲线，以去除环境噪声和土壤固有异质性产生的干扰。然后将原始B-scan图像和去除杂波后的纯净双曲线图像并行输入参数估计网络获得根半径和深度。最后，通过仿真试验和埋根试验证实该根系参数预测方法的精度和鲁棒性。

1 试验数据

本研究分为仿真和实地试验两部分，数据集由仿真数据及合成数据构成，用于模型训练及测试，实地试验数据用于验证本研究方法不同条件下的有效性及鲁棒性。

1.1 数据集构建

深度学习是数据驱动的方法，数据集对于训练至关重要，真实试验需要人工埋根，耗费人力物力，同时记录的大量标签存在误差，而全部由仿真数据构成数据集，神经网络将不能很好地适应真实数据，性能较差。为避免以上两种问题，本文构建了一个仿真数据和合成数据的数据集用于网络的训练，既保证了数据集有着真实实地情况下的多样性，也保证了标签的准确性。

数据集由3 部分构成，均质仿真数据、异质仿真数据和合成数据各1 000 组。各部分数据中都包含了不同的根分布以及各种土壤情况，每组数据都包含有一个原始的B-scan 雷达图像、其杂波图像以及对应的根目标图像。

1）均质仿真数据，使用基于时域有限差分（finite difference time domain，FDTD）方法求解麦克斯韦方程的开源软件gprMax 生成，仿真场景如图1 所示，模型尺寸为0.6 m×0.6 m×0.2 m，时间窗大小为15 ns，使用完全匹配层减小侧反射，仿真数据参数如表1 所示。使用的天线是由地球物理探测公司（GSSI）制造的400 MHz商用GPR 天线，位于土壤表面5 cm 高度处，沿检测线方向移动，每1 cm 发射一次电磁波并收集一次数据形成一个A-scan，共收集32 个A-scan 形成B-scan 图像。无杂波B-scan 图像由原始含根目标的B-scan 数据减去相同土壤条件下无根目标的B-scan 数据获得，通过这种方式去除相同位置的杂波，无杂波图像仅含有根目标反射回波信号。

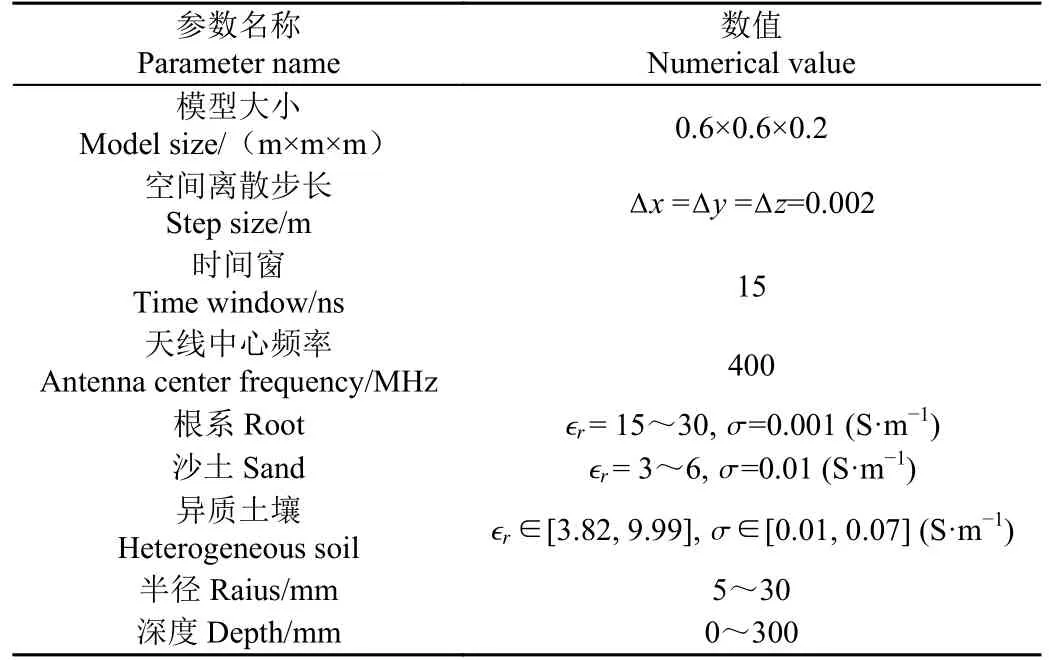
表1 数据集参数设置Table 1 Parameters settings of dataset

图1 数据集3 类型样例Fig.1 Examples of 3 types of data sets

2）异质仿真数据，除土壤条件外，其余参数与第一部分相同，异质土壤模型采用Peplinski 混合模型[17]，参数如表1 所示，土壤为50%沙土和50%黏土混合，沙土密度为2 g/cm3，黏土密度为2.66 g/cm3，含水率为0.1%～25%，相对介电常数和电导率区间分别为[3.82,9.99]和[0.01,0.07]。地下介质由以上参数范围内50 种不同的异质土壤随机分布构成。

3）合成数据，由于在真实情况下无法从原始B-scan图像中获得完美的杂波抑制图像，所以使用第一部分中的根目标图像和真实无树根的土壤B-scan 图像合成原始B-scan 图像。真实数据采集使用美国 GSSI 公司的 SIR-3 000 型400 MHz 探地雷达扫描无树根存在的土壤，如图1 所示，每1 cm 记录一个A-scan，获得5 条长2.5 m，由2 500 个A-scan 组成的B-scan。将每个B-scan 分割为200 组32 个A-scan 组成的B-scan 并归一化，与第一部分的根目标图像相加，获得含有真实土壤杂波分布的Bscan 图像，与实际雷达图相似。

数据集由3 部分共3 000 组数据构成，为保证输入图像尺寸的一致性，将所有图像统一调整为64×64 像素大小。虽然探地雷达图像大小具有实际物理意义，宽度表示B-scan 图像由多少个A-scan 组成，长度表示雷达采集数据的时间窗大小，但本文B-scan 图像中A-scan 数量及时间窗相同，所以对图像大小的统一调整不会损坏雷达图像所含的信息。最后将数据集按7:1:2 的比例分为训练数据、验证数据和测试数据。

1.2 实地数据采集

为验证本文方法对实地数据的泛化能力，2023 年3月在江南大学操场沙坑进行人工埋根试验，沙土环境便于挖掘，避免土壤挖掘产生的结块和空气间隙[13,18-19]，2023 年6 月挖掘了实际泥土土壤中的真实根系。实地试验数据采集同样使用GSSI 公司的 SIR-3 000 型400 MHz探地雷达。选取相对介电常数和根相近的树枝作为模拟根系，通过不同半径、不同掩埋深度以及不同土壤含水率的埋根试验，测试网络对真实实测数据的有效性。测量根上中下多个位置求平均半径得到，本文选取8 个不同半径的根系开展试验以验证本文方法对半径的预测效果，具体根参数如表2 所示。

表2 样本根系数据Table 2 Data of sample roots

试验分两组，第一组为干燥环境，土壤含水率低，沙土地挖掘的两个长方形试验坑，如图2a 和图2b 所示，试验坑A 深度约为50 mm，试验坑B 深度约为150 mm，宽度均为400 mm，每条根埋入后单独测量具体深度，和试验坑深度不完全相同。两试验坑均埋入根R1、R2、R3、R4，测量时向沙土的不同部分喷洒不同量水，产生不同的含水率分布，由此模拟异质土壤相对介电常数分布。两试验坑反映了对于不同树种、不同深度和不同半径的预测效果。

图2 试验现场Fig.2 The site of experiment

第二组为强降雨后24 h 内，土壤含水率高，如图2c和图2 d 所示，试验坑C 和试验坑B 相似，但坑C 含水率更高，埋入根R5 和R6，试验坑D 为实际泥土下树根，挖掘出根记为R7 和R8。两试验坑反映了不同土壤环境下预测效果。

2 研究方法

2.1 模型构建

本文方法分为两阶段，网络框架如图3 所示，第一阶段使用注意力机制改进的U-net 构成杂波抑制网络以去除天线间的耦合、地面反射直达波、地下介质随机分布的复杂性等因素导致的杂波，将原始B-scan 图像输入杂波抑制网络，然后输出仅包含根反射信号的图像。第二阶段将仅包含目标根信息的图像与包含异质土壤信息的原始B-scan 图像并行输入根参数估计网络，提取根反射信号以及异质土壤的特征，使用inception 结合全局和局部信息，最后通过全连接层输出预测值。

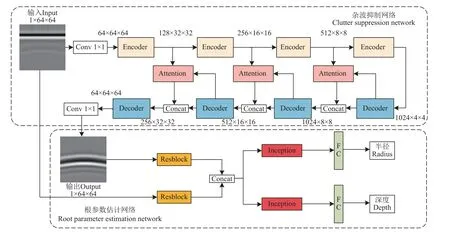
图3 本文方法网络模型Fig.3 Presnted network model

本文方法与已有的预测方法的流程对比如图4，杂波抑制网络代替目前主流方法对原始数据进行的多次预处理过程。根参数估计网络代替拟合双曲线并提取其信息的步骤。降低了实际应用复杂性，避免误差的累积。

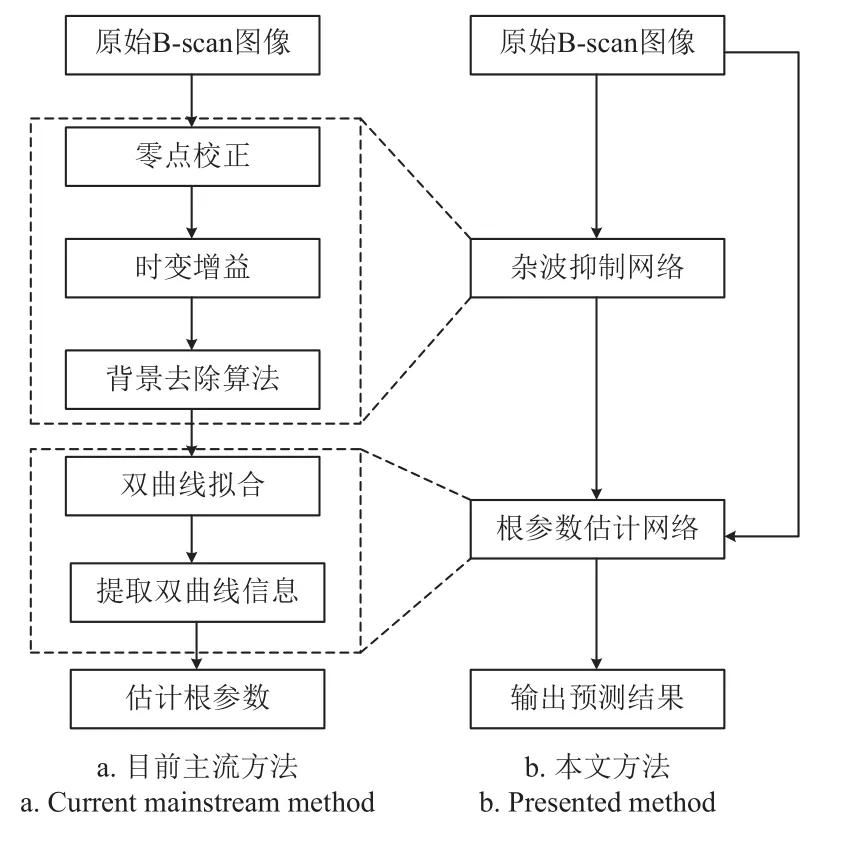
图4 流程图对比Fig.4 Flow chart comparison

2.1.1 杂波抑制网络

相比于市政工程方面[20-21]探地雷达应用于人造混凝土介质，土壤的异质性导致杂波和噪声更为明显，对目标回波的影响也更大。因此，对探地雷达原始数据进行杂波抑制是必要的。原始信号数据包含了目标回波及许多噪声和杂波，可以表示为

式中Sr为原始信号，St为根目标产生的回波信号，Sc为雷达天线耦合及土壤异质性导致的杂波信号，杂波抑制网络判断原始B-scan 图像每个像素是否为根目标产生的信号，将不属于根目标的杂波信号去除以达到抑制杂波。

本文提出的杂波抑制网络受U-net[22]启发使用编码-解码结构，并使用注意力机制改进以适应探地雷达使用场景。U-net 具有能对小数据集训练和对像素点分类以获得高准确率分割的优点，适用于解决探地雷达图像处理方法面临的挑战：图像数据样本少以及实际应用时杂波种类多干扰严重。

原始U-net 主要由三部分组成：编码器、解码器和跳跃连接。由于探地雷达数据中根反射区域比例较小，背景干扰严重。本文添加注意力模块到跳跃连接部分，使其能自适应地对根目标区域增大权重，更好地保留根反射的双曲线，减少杂波干扰。

编码器部分由四个编码块组成，如图5a 所示编码块包含两个卷积块和一次下采样操作。卷积块由卷积层，BN 层和激活函数组成，卷积核大小为3×3，步幅为1，填充为1，确保通过卷积核前后特征图大小相同。批归一化操作应用于卷积操作之后，用于稳定网络中数据的分布，加速模型的训练，并缓解梯度消失的问题。激活函数使用ReLU，其非线性映射能力可以增强模型学习能力。下采样操作由MaxPooling 实现，池化核大小为2×2，步幅为2，每次将特征图缩小为输入的一半，这有助于提取更高层次的特征。

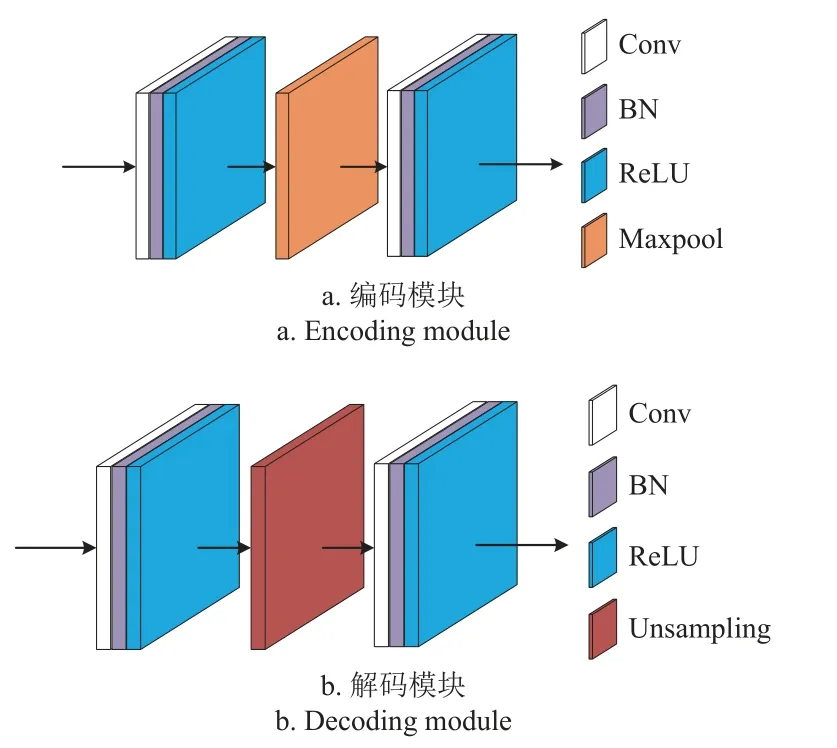
图5 编码-解码模块Fig.5 Encoding-decoding module

解码器部分和编码器类似，如图5b 所示，由两个卷积块和一次上采样操作组成的解码块 的4 次连续使用构成。上采样操作使用双线性插值实现，比例因子为2，将特征图扩大为输入的两倍，恢复丢失的空间信息，提高图像重建的精度。

使用注意力模块代替跳跃连接，将编码器压缩后和解码器解码后的同尺寸特征图作为共同的输入，通过融合浅层和深层的特征学习权重信息，注意力模块引导解码器通过网络学习的过程关注数据中根目标反射的回波信号。

注意力模块结构如图6 所示，其中X表示编码部分输入特征，Y表示解码部分输入特征，分别经过卷积和批归一化操作后相加，再经过卷积块得到权重信息，大小和输入特征相同，通道数为1。权重信息代表了网络对输入特征各部分的关注程度。最后将权重信息与输入解码部分特征相乘，以获得和输入解码部分特征相同大小和通道数的新特征。

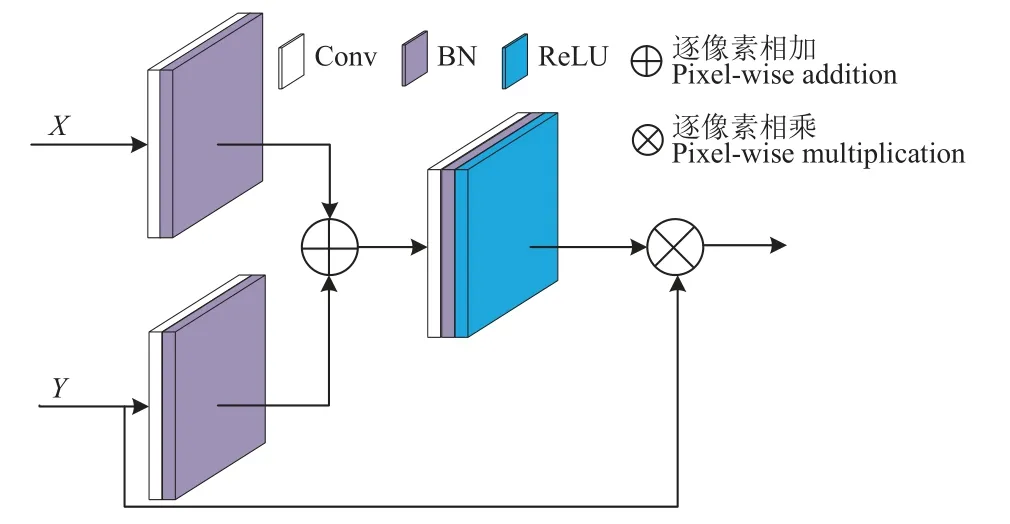
图6 注意力模块Fig.6 Attention module

2.1.2 根参数估计网络

为综合考虑异质土壤对探地雷达信号的影响以及根反射双曲线信息，本文提出一种双通道根参数估计网络，由残差块（resblock）和inception 块组成。将原始探地雷达B-scan 数据和上一阶段杂波抑制后的根目标图像并行输入，首先通过残差块，然后将2 个通道输出的特征图拼接，输入到多任务分支，每个分支经过一个inception 模块，最后通过多个全连接层（fully connected layer，FCL）将前面学习到的特征输出为根深度和半径。双通道网络充分利用异质土壤的背景信息和根目标反射的回波信息，提高根参数的预测精度。

残差模块（resblock module）：雷达图像中部分反射信号强度较小，相比其他反射无法被显著观察，但同样包含着土壤和根系的重要信息，为避免经过连续的卷积后，这些信号特征的消失，导致根参数预测精度的降低，引入跳跃连接将经过第一次卷积后的特征与最后输出的特征融合，保留浅层中重要信息的特征。如图7 所示，残差块包含3 个连续的卷积层，每个卷积层后是ReLU 激活函数。

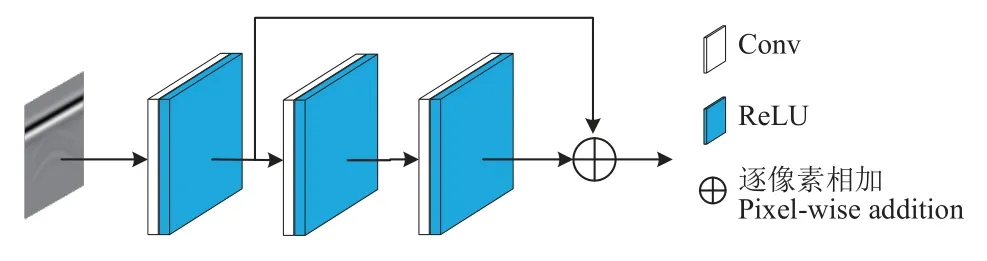
图7 残差模块Fig.7 Resblock module

inception 模块：由于地下根系位置和根半径大小的随机性，雷达图像在不同位置有着不同形状的双曲线，并且网络需要同时输出根深度和根半径，两个根参数的信息尺度不同，根深度关注全局的空间尺度，而根半径与局部信息相关性强。所以使用inception 块以获得不同的特征感受野，大的特征感受野捕捉具有高层次语义的全局信息，而小的特征感受野关注局部细节的特征，计算式如下

式中rη表示第 η 层感受野，rη-1表示第 η-1 层感受野，kη表示卷积核大小，sn表示步幅。

inception 模块结构如图8 所示，采用四分支结构，具有不同的特征感受野，分别为1×1、3×3、5×5、7×7以提取图像中不同尺度特征。随着卷积核大小增大，计算成本增加，使用连续两个和三个大小为3 的卷积核代替5×5 和7×7 大小的卷积核。最后拼接4 个分支不同尺度的特征。

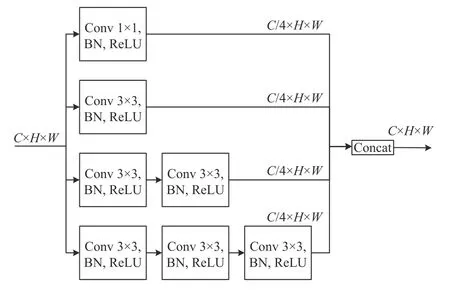
图8 inception 模块Fig.8 Inception module

为将图像特征映射到输出的根参数，最后将特征降至一维输入4 个连续全连接层，各全连接层节点分别为1 024、256、64 和1，并在第一个全连接层添加dropout层，比例为0.5，随机丢弃一半的节点数据，防止模型过拟合，增强泛化性能。

2.2 模型训练与评估指标

2.2.1 试验平台与训练参数

本文试验平台是Ubuntu16.02 系统搭载1 块CPU 处理器（Intel Core（TM）i9-9900X @ 3.50 GHz）和2 块12 G 显存GPU（Nvidia RTX2080Ti×2），采用Pytorch作为深度学习框架，版本为1.7.1，CUDA 版本为10.1，软件环境为python 3.8。

杂波抑制网络和根参数估计网络均使用均方误差（mean squared error，MSE）作为损失函数，并采用Adam 最小化预测值与实际值间的均方误差，动量为 0.9和权重衰减为1e-8，学习率分别为0.001 和0.000 8。两个模型均迭代（epoch）100 次，模型每批次样本数量（batch size）为16。

2.2.2 评估指标

对于杂波抑制，使用峰值信噪比（peak signal to noise ratio，PSNR）和结构相似性（structural similarity，SSIM）指标进行杂波抑制前后的定量分析。计算公式如下：

式中MAX为图片最大图像值，n为图像像素数量，xi为抑制后图像像素值，yi为目标图像像素值，PSNR越大表示效果越好。

式中x、y为输入的两张图片，l(x,y) 是亮度比较，c(x,y)是对比度比较，s(x,y) 表示结构比较，α、β、γ分别代表其各部分对于SSIM的权重，本文设置 α=β=γ=1，µx和µy分别代表x和y的平均值，σx和 σy分别表示x和y的标准差，σxy表示x和y的协方差，c1、c2、c3为常数，避免分母为零带来的错误，本文c1=2.552，c2=7.652，c3=c2/2。SSIM越接近1 表示效果越好。

使用平均绝对误差（mean absolute error，MAE）和决定系数（confficent of determination，R2）来评价模型对于根参数的预测效果。平均绝对误差是指预测值与真实值之差的平均绝对值；决定系数用于评价回归模型的拟合程度，决定系数越接近于1 表示拟合程度越好。

3 结果与分析

3.1 仿真数据结果

图9 展示了对原始B-scan 图像的杂波抑制效果。图9a 显示了含杂波的B-scan 图像，图9b～9f 分别给出了均值滤波（mean subtraction，MS）[23]、奇异值分解（singular value decomposition，SVD）[24]、鲁棒主成分分析（robust principal component analysis，RPCA）[25]、U-net 以及本方法杂波抑制后的图像。从图9 可以看出，MS 对于不均匀杂波抑制效果较差，且对根目标反射双曲线造成了一定的扭曲，基于子空间的奇异值分解（SVD）和鲁棒主成分分析（RPCA）将图像分解为对应目标、杂波和噪声多个分量，但目标信息存在于多个分量中，分离效果不佳，仍有部分杂波混杂在根目标反射分量中，U-net 由于缺少注意力机制，与目标双曲线重合的小部分杂波没有被去除。与其他方法相比，本文方法几乎去除了所有杂波，并保留了根反射的主要双曲线信息。

图9 仿真数据效果对比Fig.9 Comparison of simulation data effects

针对PSNR、SSIM和时间等指标，比较了各种算法的杂波抑制性能，对于测试集计算平均PSNR（dB）和平均SSIM以及计算用时（ms），比较结果如表3 所示。MS 处理时间最短，但效果最差，除RPCA 耗时较长外，其余方法处理时间相差不大，但本文方法具有最好的PSNR和SSIM。

表3 不同算法对比Table 3 Comparison of different algorithms

图10 展示了本文方法在测试数据集上的预测效果，使用不包含在训练集中的600 组数据。可以看出，拟合程度较高，大部分预测数据与真实标签差值较小。深度上93.3%的估计误差在8 mm 以内。半径上84.8%的估计误差在3 mm 以内。

对比其他回归模型，结果如表4。其他回归模型没有多任务分支，虽然可以更好地映射数据和单任务之间的关系，但是每组模型参数只能预测一个根参数，需要对根深度和根半径分别训练两组模型参数，而本文方法只需要一组模型参数就可以同时预测根半径和深度。训练集和测试集下，本文方法的根半径预测平均绝对误差是1.7 mm，R2值为0.914，根深度预测的平均绝对误差是6.3 mm，R2为0.989，优于其他常见回归模型。这是因为其他回归模型没有关注异质土壤信息，导致对于不同环境下的鲁棒性降低，土壤条件变化时无法将数据准确映射到预测值。由此可知，本文方法可以使用训练好的模型实现快速而准确的预测根半径和根深度的，提高应用效率。

表4 不同模型性能比较Table 4 Performances comparison of different models

3.2 实地埋根试验结果

将实测B-scan 数据输入训练好的模型，杂波抑制效果如图11 所示，图11a 是原始B-scan 图像，图11b～11f 是MS、SVD、RPCA、U-net 以及本文方法的杂波抑制结果。MS、SVD、RPCA 只能去除部分杂波，U-net淡化了根反射双曲线，可能导致目标根信息损失。本文方法在去除大部分杂波的同时，较完整地保留了目标根双曲线。

根参数预测结果如表5 所示，本文方法对于实地试验根半径预测最大误差为1.85 mm，平均相对误差为6.21%；对于实地试验根深度预测的最大误差为13.6 mm，平均相对误差为6.88%。因为实测数据多样性相对于仿真数据集较弱，实地数据预测效果略优于本文方法在数据集上的预测效果。实地试验根半径基本覆盖本文模型训练时使用数据集设定范围。并且使用不同树种、不同土壤环境验证，使用实测数据得到的预测结果证明了本文提出方法能够成功预测根系半径和深度，并且误差较小接近真实值。

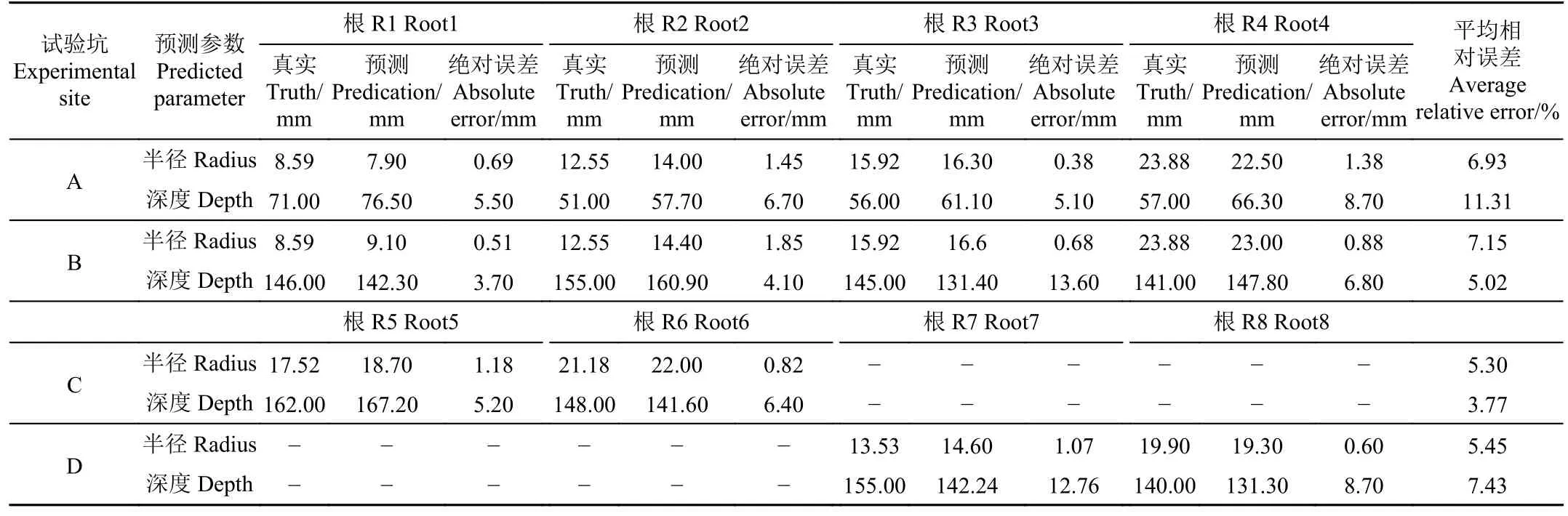
表5 样本根系预测结果Table 5 The results of sample roots prediction

4 讨论

4.1 数据集多样性

深度学习模型预测准确性与数据集大小和构成密切相关，较为多样的数据集能很大程度上提高模型的泛化能力。而探地雷达数据受探地雷达以及检测目标环境等多方面共同影响。

1）雷达频率：不同频率的雷达各有优势，高频雷达在垂直方向上具有更高的分辨率，但传播过程衰减严重，适合浅层根系检测，降低雷达频率可以获得较大的探测深度，但是随之降低的垂直分辨率可能导致无法解析根系上下表面，导致根半径的预测结果相差较大，本文使用400 MHz 雷达。

2）土壤条件：检测根系所在土壤结构含水率不同导致的异质性将产生严重的杂波，并导致反射双曲线扭曲，本文提出杂波抑制网络降低其影响，但暂时未考虑到多种地质结构分层土壤结构。

3）根系分布：本文埋根均垂直于雷达扫描路径，实际根生长过程存在倾角会导致B-scan 图像中双去线形状被拉伸变形。针对以上问题，开发一个多样性更强，样本更丰富的数据集是能够为将来的研究工作带来极大的帮助。

4.2 模型预测

本文使用B-scan 图像预测根半径和根深度，现有绝大部分雷达均是采集B-scan 数据，本文方法能方便地应用于商用探地雷达。但是含有较为集中局部信息的Ascan 数据和由多组B-scan 构成的C-scan 没有被充分利用，根系所处垂直方向的A-scan 数据中根半径和根深度相关信息比例较高，可以借助A-scan 数据提高模型预测性能，而C-scan 数据包含根系不同剖面的信息，利用信息丰富的C-scan 数据能够分析树根的方向角度。

5 结论

本文提出了一种基于神经网络的探地雷达杂波抑制和根参数预测方法，实现了对于根半径和根深度的准确预测。

1）针对探地雷达检测异质土壤介质中杂波影响检测精度的问题，提出了一种杂波抑制网络，对收集到的原始B-scan 图像进行杂波抑制，提取根目标反射双曲线，有效去除了异质土壤环境导致的不利影响，在测试数据集上获得了39.42 dB 的峰值信噪比以及0.991 的结构相似性，为第二阶段根参数估计提供了高质量的雷达图像数据。

2）提出了一种双通道根参数估计网络，实现对根深度和半径的同时预测。在数据集上对于根半径和根深度的平均绝对误差分别为1.7 和6.3 mm，决定系数分别为0.914 和0.989，优于其他常见回归模型。在实地试验中，根半径和根深度预测的最大误差分别为1.85 和13.6 mm，总平均相对误差为6.55%。证明本文预测方法准确预测根半径和根深度，具有较高的鲁棒性，能够适应不同土壤环境。