广义二项自回归模型的贝叶斯统计推断
邵思雨, 龙 琪, 张 洁
(长春工业大学 数学与统计学院, 吉林 长春 130012)
0 引 言
时间序列数据是指把具有某一个相同统计指标的数值依据它发生的日期先后顺序排列而成的数列。而取值为非负整数的时间序列数据作为一种计数数据,其研究范围更为广泛。因为这类时间序列数据只能取整值,而传统实数范围上的时间序列数据能取到小数,所以这两种数据的研究存在较大差别。一般情况下,依据非负整数值时间序列数据有无上界,可以将此数据划分成有上限的数据(0,1,…,n)和无上限的数据(0,1,…)。例如:某一地区一周七天下雨的天数数据,以及某一地区患新型肺炎的人数等。这些年,研究者为了拟合这类数据建立了不少模型。迄今为止,最常见的两种建模方法分别为基于潜过程构造的状态空间模型[1],以及基于稀疏算子提出的整数值自回归模型[2-6]。
针对取值范围有上限的整数值时间序列数据,例如长春市每天有多少个城区发生交通事故数据、全国每个月有多少城市发生地震数据等。拟合这类时间序列数据较为常见的方法是McKenzie E[7]提出的First-order binomial autoregre-ssive(BAR(1))模型。Weiβ C H[8]研究BAR(1)模型的相应性质,并将其推广到高阶情形。此后,越来越多BAR模型的衍生模型涌现[9-11]。然而,二项稀疏算子是基于独立同分布的伯努利随机变量序列提出的,所以,如果将BAR(1)模型应用到个体之间具有相依结构的数据中,可能会使该模型的拟合效果不好。基于此,Ristic M M等[12]提出一个新的算子——广义二项稀疏算子,它的提出为具有相依结构的整数值时间序列数据的研究提供了参考价值。近期,Kang Y等[13]和康尧[14]将广义二项稀疏算子应用到二项自回归模型中,得出一类一阶广义二项自回归(GBAR(1))模型,并且对该模型进行了相应的统计推断。由于此算子放松了对二项稀疏算子的独立性假设,从而对于包含相依结构的整数值时间序列数据的研究具有较大意义,并且能够有效地解决古典BAR(1)模型解释实际背景问题时的部分局限性。
对于上述模型的统计推断研究,模型相应的参数估计问题是研究的重点内容之一。除了常用的Yule-Walker 估计、条件最小二乘估计、条件最大似然估计和经验似然估计以外,贝叶斯估计也是一种对模型参数进行统计推断的方法,不少学者对贝叶斯方法进行了研究。Lazar N A等[15]针对贝叶斯经验似然检验了后验推断的有效性。张哲等[16]利用贝叶斯方法研究了First-order integer-valued autoregressive(INAR(1))模型参数的估计问题。Xi R等[17]针对spike-and-slab先验的经验似然的贝叶斯分位数回归,研究了其中非参数贝叶斯变量选择等问题。朱复康等[18]利用矩方法和贝叶斯方法研究Integer-valued generalized autoregressive conditional heteroscedastic(INGARCH (1,1))模型的参数估计问题。近期部分研究详见文献[19-20] 。
基于此,考虑针对GBAR(1)模型,研究相应的贝叶斯统计推断问题,并将该模型应用于实际数据的分析研究中。通过贝叶斯估计方法得到有效的拟合结果,为具有相依结构的实际问题研究提供理论支撑。
1 GBAR(1)模型的贝叶斯估计
Kang Y等[13]将广义二项稀疏算子 “ ∘θ”引入到BAR (1)模型中,提出一类一阶广义二项自回归(GBAR (1))模型,并且给出模型的Yule-Walker估计、条件最小二乘估计、条件最大似然估计。文中通过进一步研究给出了GBAR (1)模型的贝叶斯估计。首先给出GBAR (1)模型的定义及相关性质。
定义1如果{Xt}是有上限的非负整数值时间序列数据,并且{Xt}t∈N满足方程:
Xt=α∘θΧt-1+β∘θ(n-Χt-1),t≥1,
(1)
其中n∈N为数据上限,α、θ∈(0,1),各稀疏运算之间相互独立,则称{Xt}为广义二项自回归模型,记作GBAR(1)模型。
“α∘θ”是广义二项稀疏算子, 其定义为:
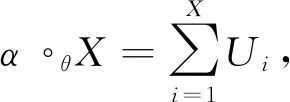
Ui=(1-Vi)Wi+ViZ,
式中:{Wi}i∈N,{Vi}i∈N----两列独立同分布的Bernoulli(α)和Bernoulli(θ)随机变量序列;
Z----一个Bernoulli(α)随机变量。
{Wi}i∈N,{Vi}i∈N和Z之间是相互独立的,α、θ∈(0,1)。
对于给定的n∈N,GBAR(1)模型的转移概率为:
P(Xt=k|Xt-1=l)=

(2)
在转移概率已知的条件下进一步考虑GBAR(1)模型的贝叶斯估计。假设X1,X2,…,XT是来自GBAR(1)模型的T个样本观测值,α,β,θ为待估参数。由式(2)可得样本的联合似然函数为
P(x|α,β,θ)=L(x|α,β,θ)=
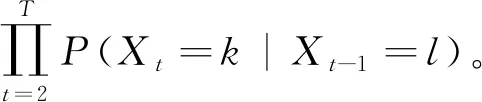
(3)
取参数α,β,θ的先验分布分别为Beta(e,f)、Beta(p,q)和Beta(h,g),这里我们分别记作π(α),π(β),π(θ),即
(4)
(5)
(6)
由此得出联合密度函数
P(x,α,β,θ)=L(x|α,β,θ)×π(α)×
π(β)×π(θ)。
(7)
在给定联合似然函数以及先验分布后,由贝叶斯原理可知,参数α,β,θ的联合后验为

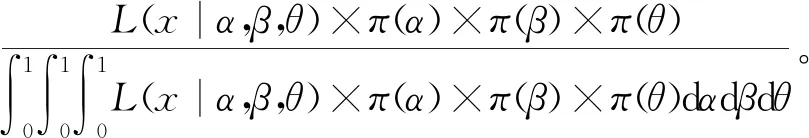
(8)
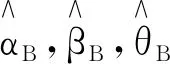
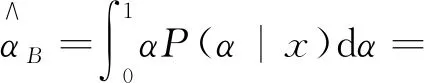
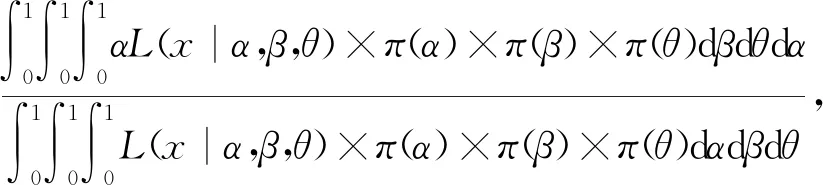
(9)
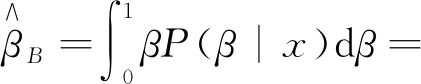
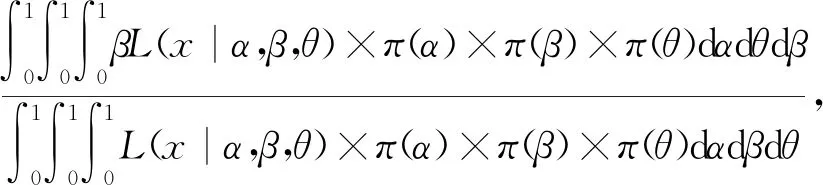
(10)
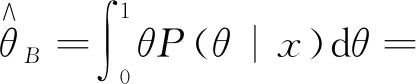
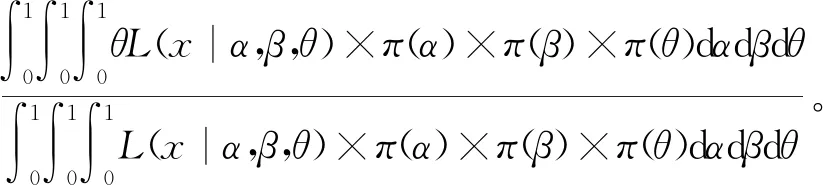
(11)
2 数值模拟
对GBAR(1)模型进行数值模拟,通过参数估计的偏差和均方误差来比较Conditional Least Squares (CLS) 估计、Conditional Maximum Likelihood (CML) 估计和Bayesian (BYE)估计的估计效果。根据参数α,β,θ的取值空间,选取以下四组不同的参数组合进行数值模拟:
1)n=5,α=0.25,β=0.75,θ=0.65;
2)n=5,α=0.40,β=0.60,θ=0.55;
3)n=8,α=0.40,β=0.20,θ=0.45;
4)n=8,α=0.80,β=0.20,θ=0.35。
选取参数α,β,θ的先验分布为贝塔分布。令贝塔分布的均值等于参数真值的方法来选取超参数,并令几组参数组合的先验分布分别为:
1)α~Beta(1,3),β~Beta(6,2),θ~Beta(2,1);
2)α~Beta(2,3),β~Beta(6,4),θ~Beta(2,2);
3)α~Beta(2,3),β~Beta(1,4),θ~Beta(1,1);
4)α~Beta(4,1),β~Beta(1,4),θ~Beta(1,2)。
鉴于在进行贝叶斯估计时,需要计算多重积分,文中采用样本平均值法求解数值积分。此方法是利用样本的均值来估计所求的定积分
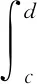
若Y服从(c,d)上的均匀分布,则有
得出定积分
I=E(g(Y))×(d-c)。
因此,当序列{Yt,t=1,2,…,N}独立同分布于(c,d)上均匀分布,则
Gi=g(Yi),i=1,2,…,N
同为一列独立同分布的随机变量序列,根据强大数定律,则有

所以
是I的强相合无偏估计,如此求解定积分的方法称为样本平均值法。
运用此法求积分
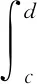
能将积分求解问题转化为求g(Y)期望的问题。在数值模拟时,样本平均值法对应的样本量N取值为105。
模拟考虑在观测数据样本量T分别为20,50,100 和200的情况下进行,最终结果是在R软件环境下取 500 次估计结果的平均值。四个参数组合的样本路径和ACF如图 1所示。
从图1可以看出, 序列为平稳时间序列,并且存在短期自相关性。
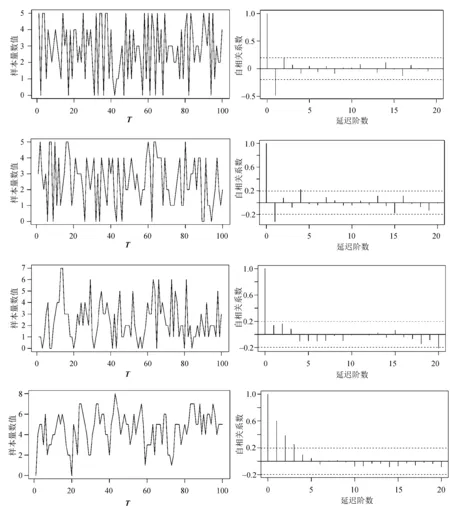
(a) 样本路径 (b) ACF
GBAR(1)模型在四组参数下CLS 估计、CML估计和BYE估计的模拟结果分别见表1~表4。
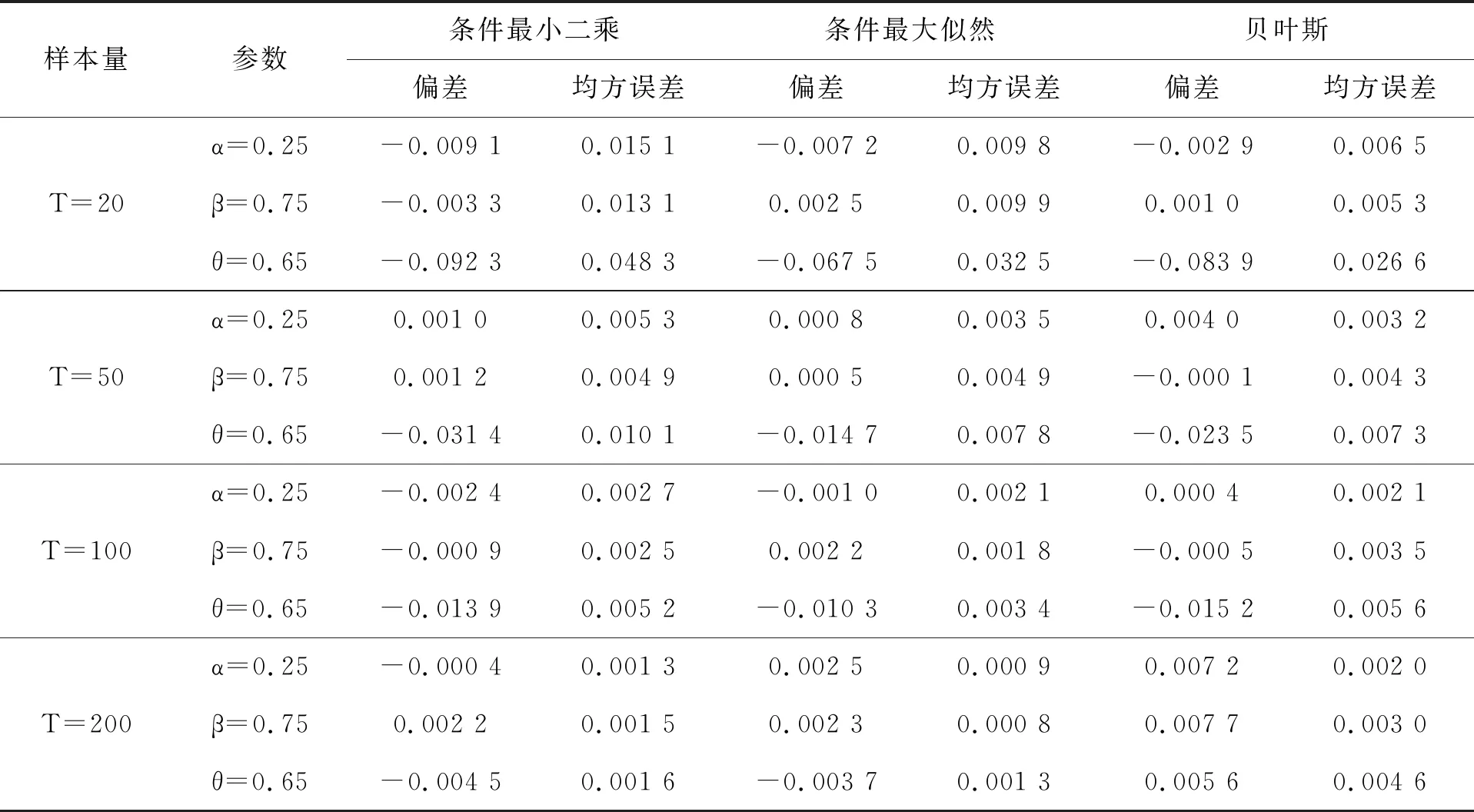
表1 第1组参数的估计结果
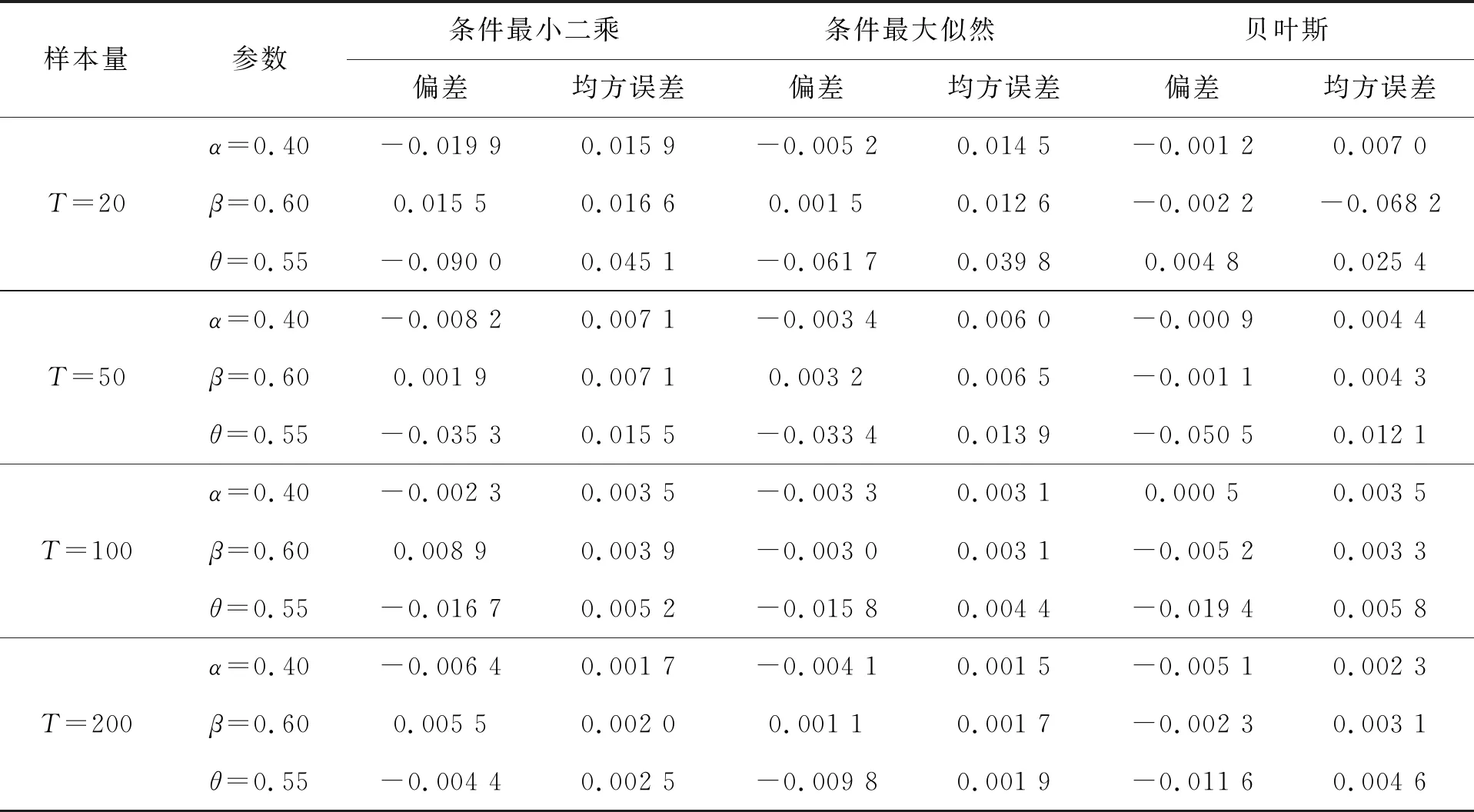
表2 第2组参数的估计结果
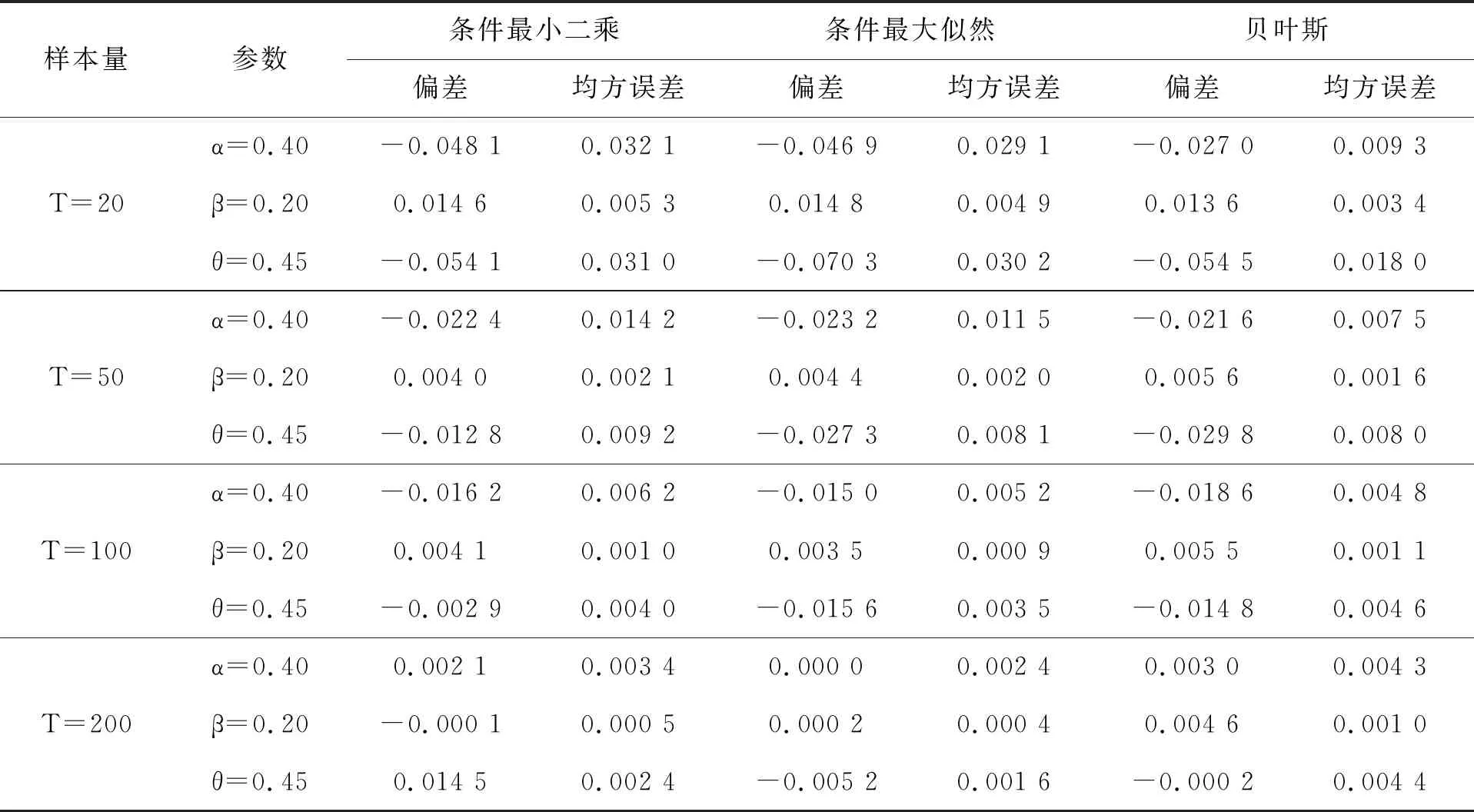
表3 第3组参数的估计结果
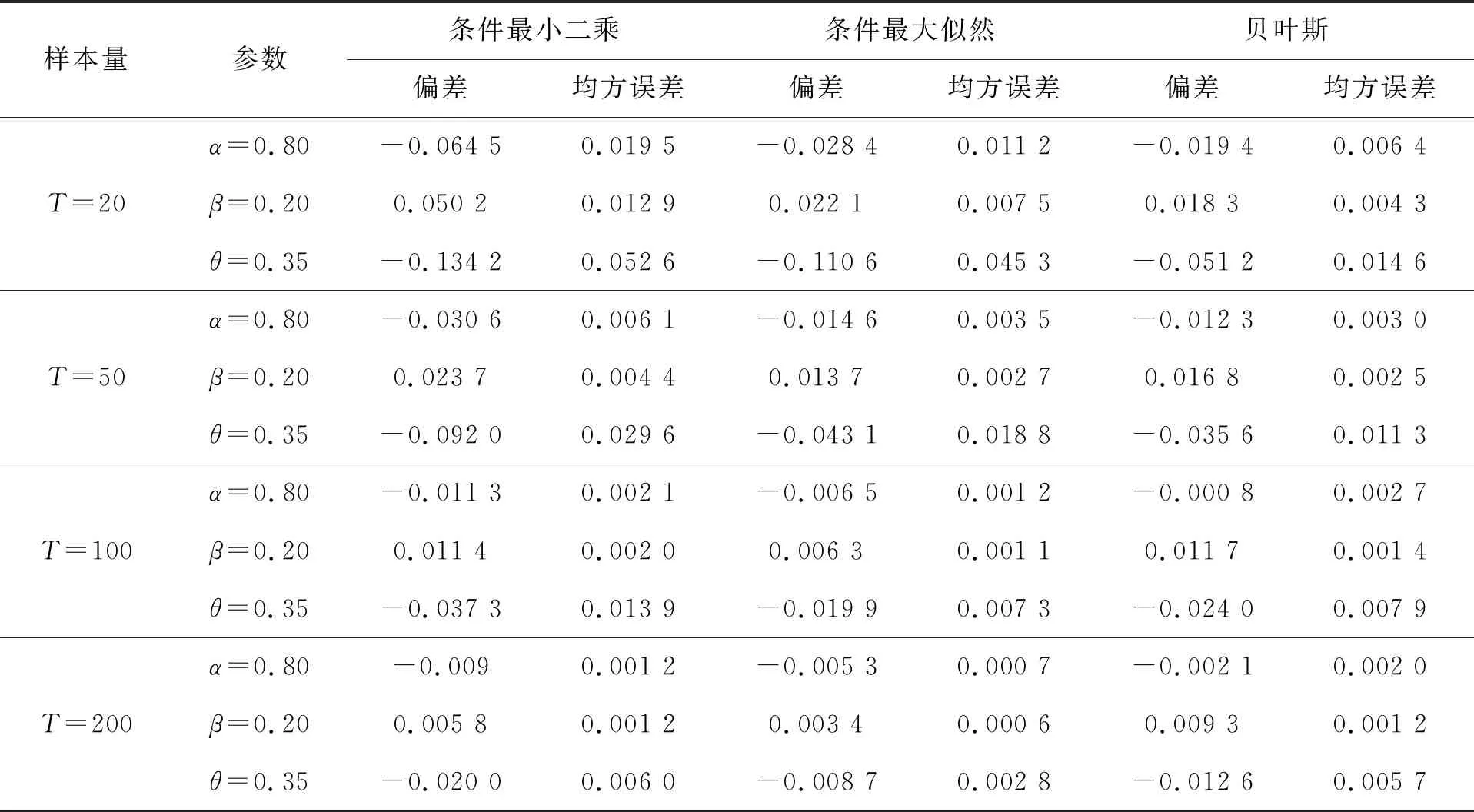
表4 第4组参数的估计结果
为了展现三种估计效果的好坏,我们用偏差 (bias) 和均方误差(MSE)两种度量指标。通过表中模拟结果可以看出,CLS、CML和BYE三种估计的偏差和均方误差都比较小,这表明以上三种估计方法的效果都比较合适。并且随着样本量的增大, 估计量的偏差和均方误差都在减小,估计效果越来越好。其次,在样本量相对比较小时,贝叶斯估计的偏差和均方误差比条件最大似然估计的略小一些,而当样本量增加后,贝叶斯估计的效果和条件最大似然估计的效果相差也不大,且贝叶斯估计的变化幅度相对较小, 后续我们通过对数据污染情况下参数估计的比较更是验证了贝叶斯估计的稳健性。
为了对三种估计方法做进一步的比较,接下来考虑三种估计方法对带污染的GBAR(1)模型的估计效果。
定义2若一个随机过程{Mt}t∈N满足方程
Mt=(1-δt)Xt+δtξt,t∈N,
式中:{Xt}t∈N----一个没有被污染的GBAR(1) 过程;
{ξt}t∈N,{δt}t∈N----一列i.i.d.的随机变量序列,分别服从B(n,p)和B(1,r);
r----污染比例,该模型为带污染的GBAR(1)模型。
样本量为100和200时,污染比例r=0.3,0.5时GBAR(1)模型的三种估计方法模拟结果分别见表5~表6。
从表中可知,对于有污染的数据,贝叶斯估计的效果要优于CML和CLS估计。由此可知,当数据存在污染时,贝叶斯估计方法更为可靠。进而说明,贝叶斯估计更加稳健,估计结果合理有效。
3 实例分析
实际生活中,有上限范围的整数值时间序列数据是很常见的,例如:某一地区一周七天下雨天数数据、全国每个月有多少城市发生地震数据等。文中从天气网中查询了2020年1月1日至2021年12月31日湖南省长沙市的历史天气,然后统计其每周下雨天数的数据情况,通过整理得到了有上限范围的时间序列数据,其中上限范围n=7,样本量为105,数据的相应统计信息见表7 。

表7 基本统计量
周降雨天数数据的样本路径和自相关图如图2所示。
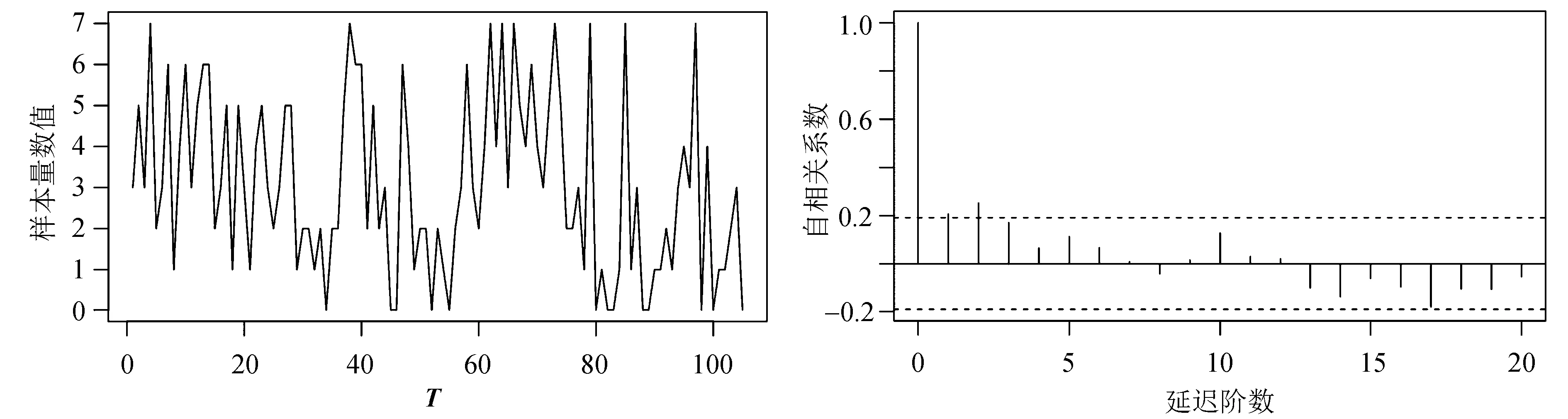
(a) 样本路径 (b) ACF
从图2(a)可以看出,数据没有向上或向下的趋势,而是在 3 附近波动,说明数据是平稳的。观察图2(b)可以看出,自相关系数在2阶后衰减到了标准差以内,也能确定序列是平稳时间序列。并且序列具有自相关性,因此用上限n=7的GBAR(1)模型来刻画这组数据是合理的。
考虑将GBAR(1)模型应用于该数据,并与文献[7] 提出的BAR(1)模型、文献[21]提出的衍生模型、BAR(1)、(IZ-BAR(1))模型和(ZIB-AR(1))模型进行比较。其中,GBAR(1)模型的贝叶斯估计中超参数设置为e=5,f=5,p=2,q=3,h=6,g=4,对应样本平均值法的N取106。
通过将GBAR(1)模型与各种其他模型参数的赤池信息准则(AIC)和贝叶斯信息准则(BIC)进行对比,用来说明GBAR(1)模型拟合的优良性。
一方面,无论是GBAR(1)模型的贝叶斯估计还是条件最大似然估计,其AIC、BIC值都小于BAR(1)模型、IZ-BAR(1)模型和ZIB-AR(1)模型,从而得出GBAR(1)模型的拟合效果优于BAR(1)模型以及其衍生模型;另一方面,GBAR(1)模型的贝叶斯估计对于样本量接近100的数据估计结果和AIC、BIC值与条件最大似然估计的相差很小,说明应用贝叶斯方法估计模型参数也能得到一个比较好的拟合效果,GBAR(1) 模型与其他模型AIC、BIC比较见表8。

表8 GBAR(1) 模型与其他模型AIC、BIC比较
进一步对GBAR(1)模型的皮尔逊残差进行分析,其中皮尔逊残差公式为
根据GBAR(1)模型的条件期望和条件方差公式,我们分别计算了GBAR(1)模型在贝叶斯和条件最大似然两种估计方法下残差的均值和方差。认为拟合残差的均值和方差越接近0和1,模型的拟合效果越好。在本节实例数据中,所拟合的贝叶斯方法下GBAR(1)模型残差的均值和方差分别为0.025 6和1.293 3。该结果也再次说明GBAR(1)模型拟合这组数据是合适的。
4 结 语
为了进一步研究具有相依结构的广义二项自回归模型的参数估计问题,充分利用样本信息、总体信息,以及通过历史经验或者规律得到的参数的先验信息,求得GBAR(1)模型参数的贝叶斯估计表示式。证明了对于GBAR(1)模型在小样本情况下,贝叶斯估计的效果要优于条件最大似然估计和条件最小二乘估计。通过对带污染的GBAR(1)模型进行数值模拟,验证了贝叶斯估计方法的稳健性。最后将GBAR(1)模型应用于长沙市下雨天数据集进行拟合,与几类二项自回归模型进行比较,得到最小的AIC与BIC值。表明GBAR(1)模型的拟合效果优于BAR(1)模型以及其衍生模型。

