一种新的全局优化鲸鱼群算法(Global_WOA)
李东升, 李万龙, 刘祥坤
(长春工业大学 计算机科学与工程学院, 吉林 长春 130102)
0 引 言
近年来,研究人员对群体智能算法的优化(SI)变得非常热衷。因为群体智能优化算法可以高效率解决许多实际问题。元启发式算法(Meta-heuristic)是基于计算智能的机制求解复杂优化问题最优解或满意解的方法,有时也被称为智能优化算法(Intelligent optimization algorithm)。元启发式算法是通过对生物、物理、化学、社会、艺术等系统,或领域中相关行为、功能、经验、规则、作用机理的认识,而提出优化算法的设计原理,并在特定问题特征的引导下提炼相应的特征模型,设计出智能化的迭代搜索型优化算法。启发式算法主要分为三类:基于进化的算法、基于群体智能的算法和基于物理现象的算法。
鲸鱼群优化该算法的主要思想是通过模仿鲸鱼的捕食行为实现对目标问题的求解。Mirjalili S等[1]提出一种群体智能算法,它具有原理简单、操作简单、易于实现的显著优点。因为它依赖于简单的概念,包含的算子较少,因此引起了许多学者的关注。但是,WOA在解决优化问题方面仍然存在缺陷。
1 相关研究
近年来,WOA的研究主要分为工程应用和理论创新两个方面。在工程应用中,WOA的实际应用主要基于其操作方便、性能优良的特点。钟明辉等[2]提出一种随机调整控制参数的鲸鱼优化算法;Rkennedy J等[3]提出粒子群算法;沙金霞[4]通过改进鲸鱼算法并应用在多目标水资源优化配置中也取得了良好的效果;Rashedi E等[5]提出一种引力搜索算法,在目前的人工智能应用中也有很好的效果;Mehne H H等[6]提出一种基于 Levy飞行的变体来增强WOA的性能;Mafarja M等[7]提出鲸鱼优化算法在数据集的特征选择中具有更好的选择效果,尤其是在搜索最优特征子集时;Abdel-Basset M等[8]提出一种将WOA(称为HWOA)与本地搜索策略相结合的新算法;Sayed G I等[9]提出一种针对数据聚类问题的多群鲸鱼优化算法(MsWOA);郭振洲等[10]提出一种基于自适应权重和柯西变异的鲸鱼优化算法;龙文等[11]通过求解大规模优化问题而改进鲸鱼优化算法;王坚浩等[12]提出基于混沌搜索策略的鲸鱼优化算法;何庆等[13]提出一种混合策略改进的鲸鱼优化算法。以上研究结果表明,鲸鱼应用优化算法解决实际问题,取得了好的结果,鲸鱼优化算法性能值得肯定,具有重要意义。
2 原始鲸鱼算法的基本思想
鲸鱼优化算法的数学模型相对于其他比较流行的群智能算法的数学模型比较简单[14],参数也相对较少,对其参数优化也容易,原始鲸鱼优化模型大致分为三个阶段。
2.1 包围猎物
因为座头鲸能识别猎物的位置并包围它们。但是算法的全局最优位置没有优先级,所以在鲸鱼群算法(WOA)的最初设定中,假设最优解位置是猎物的位置或是最接近猎物的鲸鱼位置,然后,其他鲸鱼向最优解的位置通过变换位置来进行靠拢[9],此行为表示为
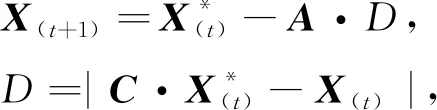
(1)
式中:t----当前迭代;
A,C----系数向量;
X*----迄今为止获得最佳解的位置向量;
X----位置向量;
·----逐个元素的乘法。
A=2ar-a,
C=2r,
(2)
式中:a----在迭代过程中从2 线性减小到0(在探索和利用阶段);
r----[0,1] 中的随机向量。
搜索代理的位置(X,Y)可以根据当前最佳记录(X*,Y*)的位置更新。通过调整“A”和“C”向量的值,可以在当前位置实现最佳代理周围的不同位置。
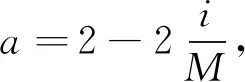
(3)
式中:a----参数;
i----当前代数;
M----总的迭代次数。
2.2 螺旋气泡网攻击
因为座头鲸的捕食行为是通过泡泡网攻击的方式来得到食物,所以对泡泡网攻击行为进行数学建模设计的两种方法为收缩环绕机制和螺旋上升机制。
1)收缩环绕机制是由系数A控制,当A≤1时,当前鲸鱼开始向最优解靠拢,并且在这个过程中,当前代理的位置可能是原始位置和当前最佳代理位置之间的任意位置。但是系数A又是由其中的参数a来控制,a是一个[-A,A]区间内的随机值,过程中从2线性下降到0,当达到0时,表示当前鲸鱼的位置已经是最优解的位置。
2)螺旋上升机制(螺旋更新位置)的建立是通过先计算出当前鲸鱼搜索代理(X,Y)和最佳位置的鲸鱼(X*,Y*)之间的距离。然后在两者之间建立一个螺旋方程,并模拟座头鲸的螺旋捕食行为,
X(t+1)=D·ebl·cos(2πl)+X(t),
(4)
式中:D----第i条鲸鱼到猎物的距离(迄今为止获得的最佳解);
b----用于定义对数螺旋形状的常数;
l---- [-1,1] 中的随机数。
结合前面描述,座头鲸在整个捕食过程中,会在缩小的圆圈内围绕猎物游动,同时沿着螺旋形路径游动。通过一个随机数P[0,1]来假设有50%的概率在优化过程中选择收缩环绕机制或螺旋模型来更新鲸鱼的位置[10]。 对应的数学模型为

(5)
这是我们在探索群智能算法勘探和开发过程中的开发阶段。
2.3 搜索阶段
座头鲸除了捕食行为外,还有寻找猎物的过程,下面就是对座头鲸寻找猎物行为的描述。在前面描述座头鲸泡泡网攻击行为的时候,已经明确座头鲸的捕食行为和寻找猎物行为之间的交替是基于系数A向量的变化而决定的。 因此,在搜索阶段,我们使用大于1或小于-1的随机值A来强制搜索代理远离参考鲸鱼。与开发阶段相比,在探索阶段根据随机选择的搜索代理,而不是迄今为止找到的最佳搜索代理来更新搜索代理的位置[11]。 这种机制和|A|>1 强调探索并允许WOA算法执行全局搜索。数学模型为
D=|CXrand-X|,
X(t+1)=Xrand-A·D,
(6)
式中:Xrand----从当前种群中选择的随机位置向量(随机鲸鱼)。
事实上,座头鲸是根据彼此位置随机搜索的。
3 改进的鲸鱼优化算法
WOA算法成功的因素之一是勘探能力和开发能力较其他群智能算法较优,但是随着时间的增长,在实际应用中也暴露出较多缺点,如精度低、收敛速度慢、易涉及局部最优等。所以,近几年有许多学者在优化鲸鱼群算法上继续做着努力,文中对鲸鱼算法优化的几个策略能够很好地提高该算法的勘探能力和开发能力。
在前人优化策略中就有单独对WOA算法的距离控制参数A进行优化,得到的效果也比较显著。因为它在整个算法中是在探索和开发之间找到适当平衡的主要因素。文中优化策略不是继续寻求勘探与开发之间的平衡,而是单独地对勘探和开发阶段进行优化,也就是整体全面的优化[12]。
3.1 勘探阶段优化策略
在鲸鱼群算法的勘探阶段,就是当前搜索代理发现猎物不是最优,会向外继续搜索猎物。当然这个行为通过学者们抽象用一个系数A的范围来控制,当|A|≥1时,就会向外搜索,也就是该算法的勘探阶段。
在实际的座头鲸群搜索猎物过程中,参照随机鲸鱼更新自己的位置,肯定不是在原始的搜索猎物模型中,可以看出,当前搜索代理在找参照搜索代理,更新自己的位置时,参照的搜索代理目标比较单一,因此也就在全局范围内搜索猎物存在缺陷,容易造成向单一方向寻找,造成局部最优的结果。所以,文中通过优化原始搜索猎物的数学模型,引入随机因子Xrand来扩大当前鲸鱼的搜索范围,使当前鲸鱼在整个范围内寻优,得到的值也能达到最优,优化后的数学模型为
X(t+1)=kXrand 1(t)+(1-k)Xrand 2(t)-AD3,
D3=|kCXrand 1(t)+(1-k)CXrand 2(t)-X(t)|,
(7)
式中:k----(0,1]之间的一个随机数;
D3----当前搜索代理到随机代理之间的距离。
3.2 开发阶段优化策略
群智能优化算法中的开发阶段是当前收缩代理,开始根据周围的搜索代理逐渐向猎物(最优解)的位置靠拢,直到在代数的迭代下达到最优值的一个过程。这就是常在群智能算法中看到的开发阶段。
3.2.1 在包围猎物阶段引入随机因子
在鲸鱼群算法的开发阶段,也就是该算法的经典捕猎行为:泡泡网攻击机制是由两个不同机制共同构成鲸鱼的捕猎行为,如环绕机制和螺旋上升机制;在实际捕猎中,鲸鱼进行环绕机制时,并不是所有鲸鱼单一地向立体空间中规定的某一处(猎物)靠近,而是会在这个捕猎空间中,随机地对比是否还有较优的值存在,如果存在,则会向最优值靠拢,这也会跳出群智能算法中常有的造成局部最优的弊病[13]。
在优化的包围猎物阶段策略引入空间随机因子,在迭代过程中,当前搜索代理会比较空间内是否还有其他搜索代理的位置是最优的。数学模型为
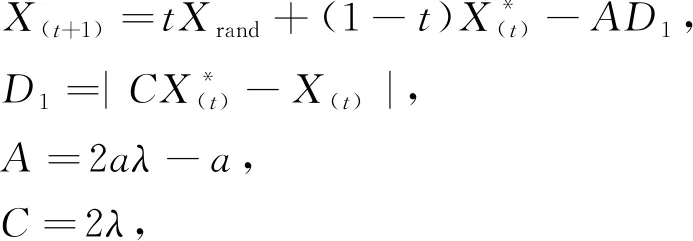
(8)
式中:t----(0,1]之间的一个随机数;
Xrand----空间中的随机因子。
3.2.2 在螺旋上升阶段引入增强开采能力因子Q
在鲸鱼群智能算法的开发阶段,另一个机制就是螺旋上升机制。在原始的螺旋上升机制中,迭代过程时,当前搜索代理通过不断地参照搜索空间中其他搜索代理的位置来更新自己的位置,最终达到最优解的目的[14]。因此,文中优化螺旋机制的策略中,引入的因子Q可以提高算法的收敛速度,能够将寻找到的解更加逼近最优解,并能够很好地跳出局部最优,最终提高了算法的开发阶段。因子数学模型为
Q=2e-5k,
(9)
优化后的螺旋机制数学模型为
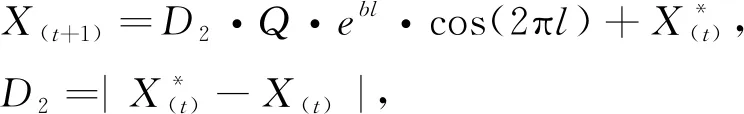
(10)
式中:k----当前迭代次数和总迭代次数的比;
b----一个常数1。
4 实验仿真与分析
算法仿真测试均在Intel Core i5-6500 CPU、3.2 GHz主频8 GB内存,以及 Windows 764 为操作系统的计算机上实现,编程软件为Annocoda中的Spyder,引入6个典型基准测试函数进行测试,见表1。
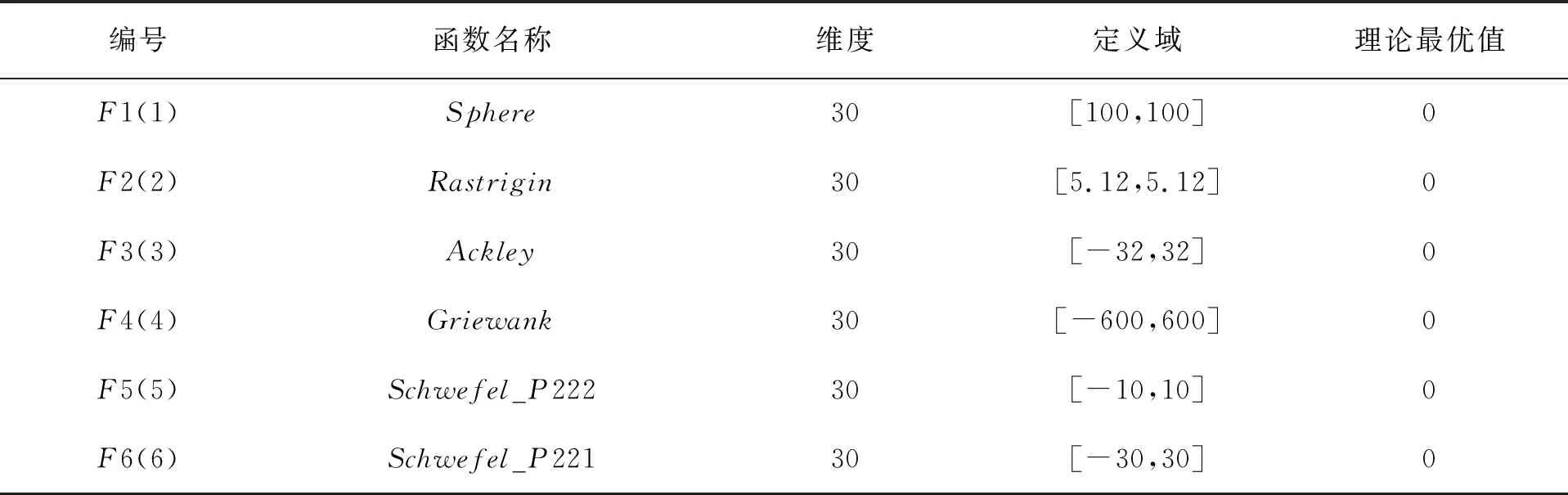
表1 基准函数
其中:F1~F5为连续单模函数; F6为复杂非线性多模函数。
文中对算法的测试主要包括以下三个部分:
1)在相同的种群大小和迭代次数条件下,比较改进算法和传统的WOA算法、传统的GWO算法在基准测试函数上算法的收敛速度和寻优精度,并证明改进的WOA算法各项性能的提升;
2)对改进的WOA算法在不同策略下进行独立测试,根据测试结果分析各种策略对WOA性能的影响;
3)与其他研究人员对鲸鱼算法的改进对比,证明其具有较强的竞争力。
传统WOA参数见表2。
4.1 改进策略对算法性能影响
为了对比不同改进策略对GLOBAL_WOA算法性能的影响,参数用上述实验的参数,策略一是对WOA中勘探阶段的数学模型进行改进,并用WOA_1来标记;策略二是通过对WOA算法开发阶段的搜索猎物数学模型进行改进,并用WOA_2来标记;策略三是对WOA中开发阶段的螺旋上升气泡网攻击猎物阶段的数学模型进行改进,并用WOA_3来标记。
不同策略下的改进算法对比见表3。
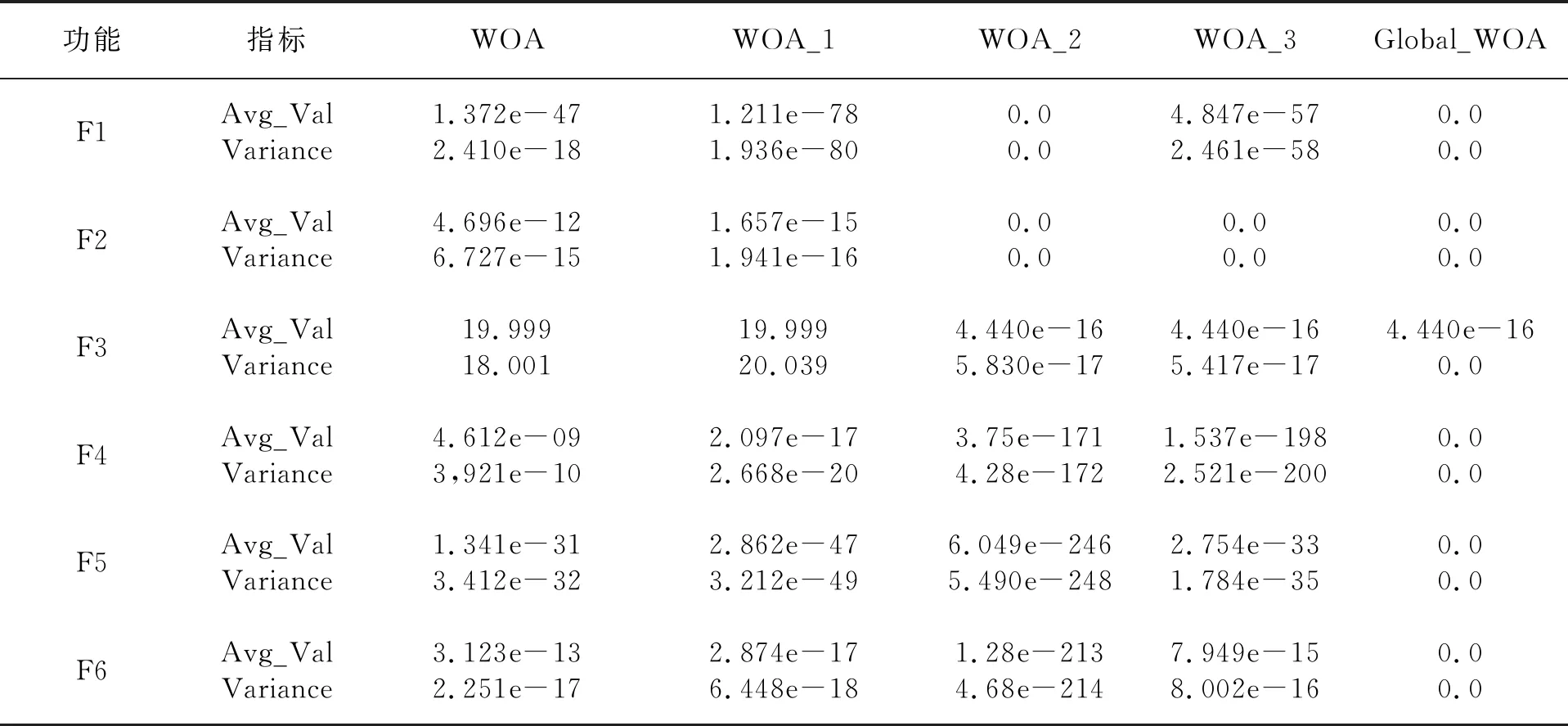
表3 不同策略下的改进算法对比(最优适应度值)
实验结果表明,在策略一(WOA_1)和策略二(WOA_2)的改进下,可以增强初始WOA的寻优进度这个性能指标,而策略三(WOA_3)的引入主要提供了算法的收敛速度。
算法收敛曲线对比如图1所示。
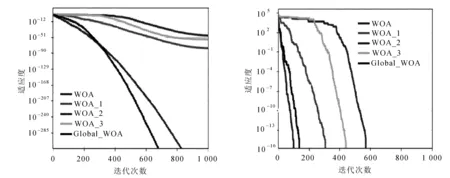
(a) fitness1 (b) fitness2
4.2 与其他改进WOA性能对比
将改进的WOA和其他研究人员对传统WOA的改进算法作对比实验,对比改进算法性能优劣。参数设置最大迭代次数为1 000,种群规模为20,维数为30,基准测试函数用上述实验用的函数,比较最优解的均值和标准差,测试结果见表4。
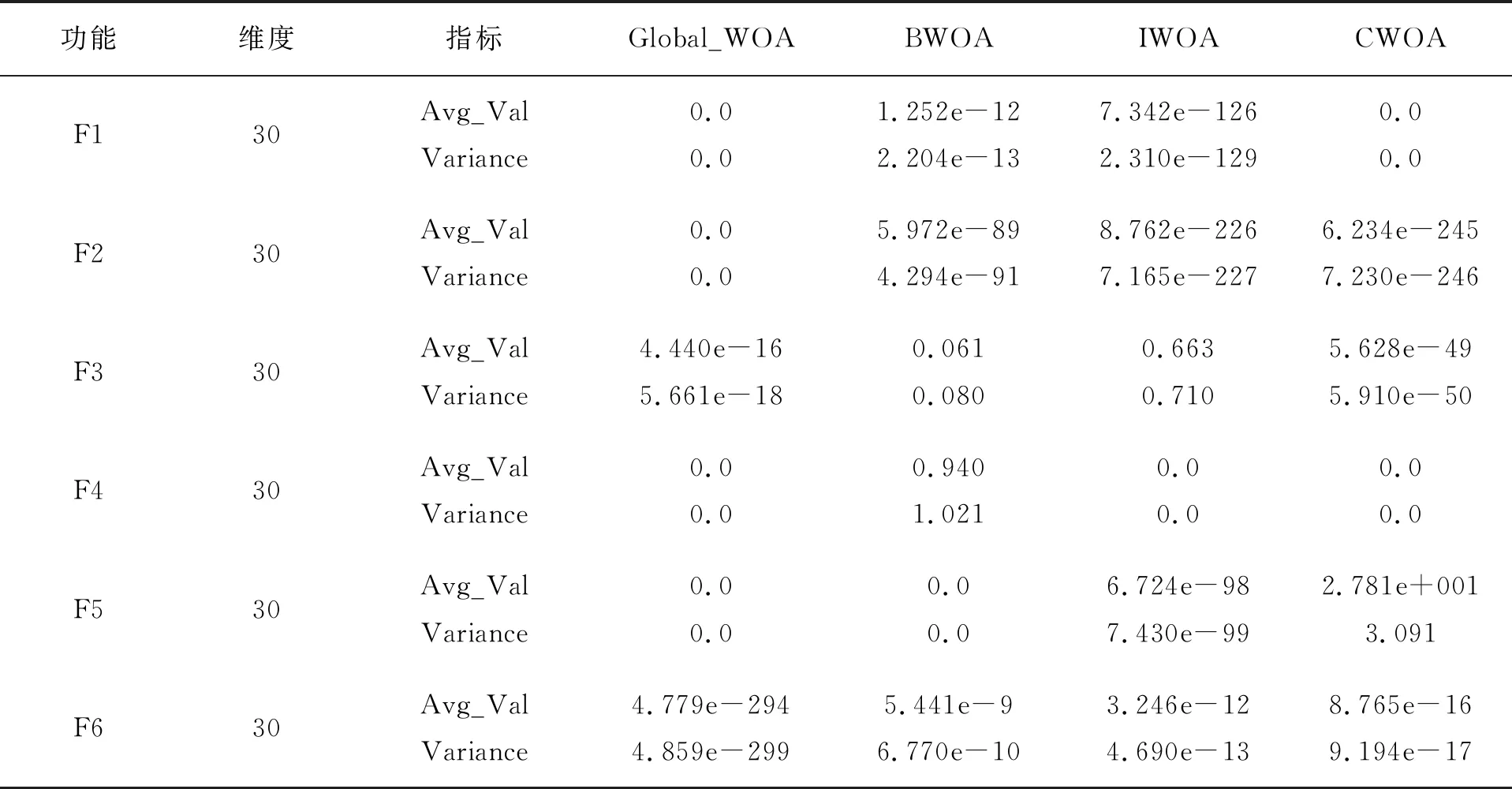
表4 不同改进算法的基准函数的对比
实验结果表明,改进的WOA算法相较于其他改进算法在寻优精度和收敛速度等方面有较强的竞争力[15]。
5 结 语
WOA 作为一种新型启发式优化算法,它与其他元启发式优化算法类似,在求解复杂函数优化问题时,存在收敛速度慢、易陷入局部最优的问题。考虑在算法迭代过程中,鲸鱼捕食策略的选择,以及位置更新对算法寻优性能的影响,在勘探阶段引入随机因子来扩大搜索范围,从而得到较优结果,在开发阶段的螺旋上升阶段引入随机因子来找到范围内的最优值,在气泡网攻击阶段引入收敛因子Q,三种改进策略对 WOA 进行改进,提高其初始算法的收敛速度和寻优精度。通过对 6 个基准测试函数仿真结果表明,改进算法的寻优精度及收敛速度均有大幅提升,并且相较于其他改进算法仍具有明显优势,证明了提出的改进策略能够使算法在求解复杂函数优化问题时具有更好的优化性能。而如何将改进算法应用于约束优化问题以及复杂的实际工程问题将是下一步主要研究的内容。

