如何帮助学生理解“积的变化规律”

陈金波

教学中，教师可以引导学生利用直观图式，通过不完全归纳的方式，帮助学生深入理解“积的变化规律”。具体可以采用以下教学方式。

一、利用直观图式，感知规律

1.直观感知，初步感知

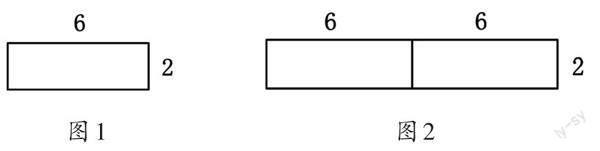
教师呈现图1，让学生列式计算这个长方形的面积是多少。接着呈现图2，让学生列式计算大长方形的面积是多少。引导学生思考：比较图1中的长方形和图2中的大长方形，什么变了？什么没变？

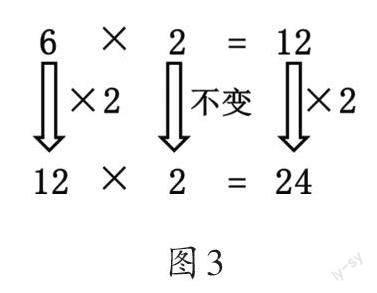
教师根据学生的回答，逐步呈现箭头图（如图3）。

得出结论：在乘法算式中，一个因数乘2，另一个因数不变，积也乘2。

2.自主探究，发现规律

教师给出学习任务：在学习单上画一个由四个图1这样的小长方形组成的大长方形，并写一写长方形的长、宽和面积会发生怎样的变化。

逐一反馈不同的学生作品。

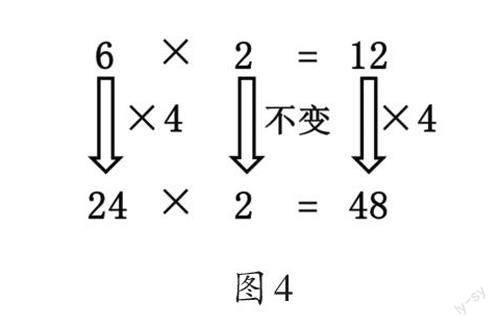
学生作品1：长方形的长变化，宽不变（如图4）。

得出结论：在乘法算式中，一个因数乘4，另一个因数不变，积也乘4。

学生作品2：长方形的长不变，宽变化（如图5）。

得出结论：在乘法算式中，一個因数不变，另一个因数乘4，积也乘4。

学生作品3：长方形的长和宽都发生变化（如图6）。

得出结论：在乘法算式中，一个因数乘2，另一个因数乘2，积乘4。

3.比较算式，猜测规律

通过比较图3、图4、图5、图6中的算式，猜想：因数和积之间存在什么样的规律？

二、通过不完全归纳，形成规律

1.独立思考

通过对这些算式的观察、比较，发现因数和积之间存在共同变化的规律，那么在其他乘法算式中是否也有这样的规律呢？

2.举例验证

先写一个乘法算式，然后分别观察一个因数不变，另一个因数发生变化，以及两个因数都发生变化两种情况下积会怎样变化。

3.形成规律

通过举例验证，学生发现有举不完的例子。在此基础上，让学生用语言表达规律。

三、借助多维度观察，完善规律

1.多维度观察

通过观察小长方形组合成大长方形时其长、宽和面积的变化，学生已经发现了因数和积之间的部分变化规律。在此基础上，组织小组讨论：如果将大长方形缩小为小长方形（如图7），你能发现什么规律？

2.完善规律

在原有举例的基础上，让学生画一画、写一写，说一说新的发现，完善对规律的认识。特别是要引导学生思考：为什么要“0除外”？

3.质疑问难

引导学生根据自己的学习过程提出问题，如：在乘法算式中，一个因数乘4，另一个因数除以2，积会怎样变化？

以上教学通过层层推进，让学生在不断学习进阶中，逐步理解积的变化规律。