高应变率加载自由水对全饱和木材原料解离强度的影响1)
许威 曹军 花军 陈光伟
(东北林业大学,哈尔滨,150040)
纤维板产业的发展实现了木材资源的综合利用,在纤维板生产中纤维分离所消耗的能源较大,消耗掉的成本较高,其直接影响了纤维板产品的成本、利润[1-4]。如何降低纤维板生产过程中的能耗,提升人造板产品的市场竞争力,一直是人造板生产企业和相关学者研究的重要内容。
国外学者对木材原料的解离动力学及其相关影响因素进行了大量研究,深入揭示了木材原料的研磨解离机制,可根据纤维板产品的性能要求,合理设置纤维解离生产的工艺参数,消耗最少的能耗,得到高质量的纤维板产品[5-9]。
国内学者利用准静态加载试验,研究了含水率对木材力学性能的影响[10]。刘昊等[11]研究了含水率、密度对木材应力波传播速度的影响,研究表明木材应力波传播速度与含水率呈负相关关系,同一树种内应力波传播速度与木材密度呈正相关关系;李猛等[12]利用声发射技术研究了0.2 mm·s-1压缩加载条件时,不同含水率杉木试件的损伤过程,研究发现木材内部损伤程度可由声发射累计振铃计数、振幅反映;骆雪等[13-14]研究了含水率对木材细胞壁弹性模量、硬度、孔隙分布的影响,研究表明含水率与木材细胞壁的弹性模量、硬度呈负相关关系,与细胞壁的孔隙体积呈正相关关系。国内学者主要研究了木材含水率在没达到纤维饱和点时,对木材力学性能的影响,而含水率超过纤维饱和点达到全饱和时,水分对木材动力学特性影响的研究较少。
本研究的目的是通过对全饱和木材试件进行高、低应变率压缩加载试验,分析全饱和木材试件内部的自由水对木材原料研磨解离动力学特性的影响,旨在深化木材原料研磨解离机制的研究,并为木纤维生产工艺参数设定、相关分离设备的结构优化设计提供理论依据。
1 材料与方法
选取纤维板生产中常用的杨树(PopulusdavidianaDode)木材作为试材,试件尺寸参照实际生产中木材原料的尺寸,25 mm×25 mm×20 mm(长、宽、高),其中高度方向为加载方向。试验测量了低应变率(0.001 s-1)、高应变率(400、700、1 000 s-1)在径向、弦向、轴向上全饱和试件的抗压强度。
试验在室温(约20 ℃)条件下进行,将加工好的试件浸入水中待试件含水率达到平衡(试件的含水率即为全饱和)。利用万能力学试验机进行低应变率加载试验,试验测得加载过程中试件的应力-应变关系曲线,并用摄像机记录加载的全过程;利用分离式霍普金森杆进行高应变率加载试验[15],试验所用霍普金森杆为铝杆,直径为40 mm,其中入射杆、透射杆的长度均为1.8 m,并在距试件1 m处粘贴应变片用于测定脉冲信号,子弹的长度为0.3 m。通过对采集到的脉冲信号进行处理,获得加载过程中试件的动力学特性,并用高速摄影机记录加载的全过程,试验后用数码相机采集加载后试件的解离图像。
2 结果与分析
2.1 试件受载后的形态特征及其抗压强度分析
2.1.1 试件受载后的形态特征
低应变率加载时,随着加载进行,试件被逐渐压缩,有大量的自由水从试件表面缓慢流出,径向、弦向加载试件流出的自由水量大于轴向加载试件。受载后径向、弦向受载试件在轴向端面上,可见沿加载方向的贯穿性裂纹,轴向受载试件在径向、弦向端面上沿加载方向产生明显的褶皱现象(图1)。

图1 低应变率加载试件解离图
对于高应变率加载,径向、弦向加载时,可观察到随着加载的进行,试件被逐渐压缩,同时有水从试件的自由端面喷出(图2);轴向加载时,无明显的水喷射现象。因此,可知受载过程中,自由水获得了大量的动能并在试件内部高速流动。高应变率加载时,随着加载应变率增加,试件的解离程度也增加,弦向加载最易解离,轴向加载最难解离,轴向加载后在试件的径向、弦向端面产生了褶皱现象(图3)。

图2 径向、弦向加载(应变率为400 s-1)时高速摄影拍摄试件自由水喷射图

图3 加载(应变率为700 s-1)试件解离图
2.1.2 试件的抗压强度
对比分析各组试验试件的抗压强度可以发现,当应变率相同时,轴向加载试件抗压强度最大,径向加载抗压强度最小;当应变率从400 s-1增加到1 000 s-1时,径向、弦向加载试件的抗压强度呈先增大后减小的变化趋势,轴向加载试件的抗压强度与应变率成正比,但是抗压强度随应变率增加的幅度变小,具有明显的应变率效应(表1)。
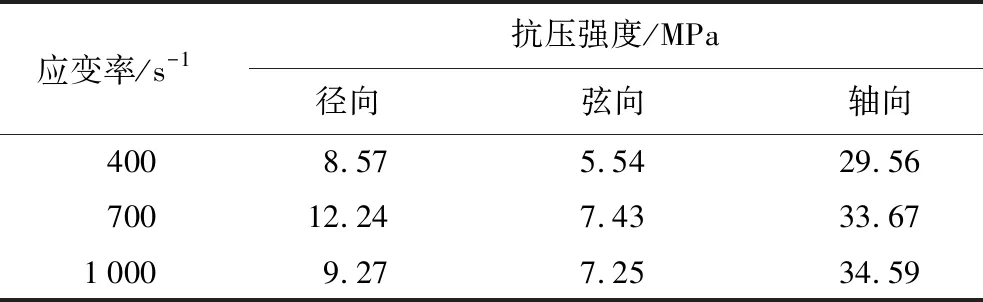
表1 杨木试件抗压强度
2.2 试件内部自由水的流动特性分析
全饱和试件内部的水分主要是结合水和自由水,结合水使木材发生膨胀,起到削弱木材试件强度的作用;低应变率加载时,自由水对木材试件强度没有任何影响,但是高应变率加载时,自由水对杨木试件强度的影响作用显著。高应变率加载时,自由水获得了大量的动能,当水具有大量动能时,其将具有巨大的破坏力[16]。
2.2.1 试件内部自由水的流态
将试件内部自由水在单一方向上的流动路径简化为圆柱管,自由水的流态可依据其雷诺数来判定。试验条件下,水的运动粘滞系数(υ,1.011×10-6m2·s-1)[17],以杨木内部尺寸最大的导管分子内径作为流动路径的直径(d,57 μm)[18];选择加载应变率1 000 s-1时,质点的速度约20 m·s-1作为自由水的流速(v),计算加载过程中试件内部自由水流动的雷诺数(Re)公式为:
Re=(v·d)/υ。
(1)
试件内部自由水流动的雷诺数为1 127.60,其小于临界雷诺数(2 300.00)。因此,当加载应变率小于等于1 000 s-1时,试件内部自由水的流态为层流。
2.2.2 试件内部自由水的流动路径
自由水沿轴向流动的路径主要是导管,通过导管上的穿孔进入到纵向相邻的导管,沿径向、弦向可以通过导管壁上的纹孔移动。因此,自由水在试件内部沿径向、弦向、轴向的流动路径可简化为直径、长度各不相等的复杂圆柱管网。由于轴向加载时无明显的水喷射现象,可只研究径向、弦向加载的情况,径向、弦向自由水的流动路径可简化为分叉圆柱管网的流动(图4)。
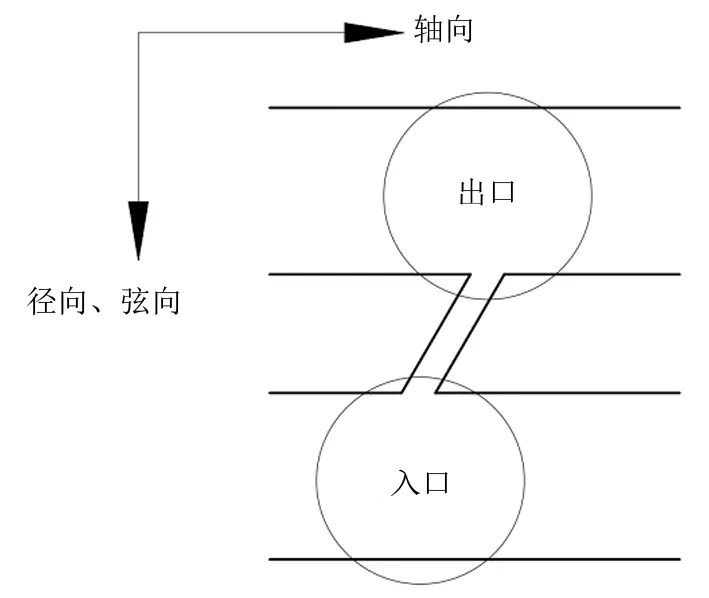
图4 径向、弦向自由水流动路径的简化图
2.3 高应变率作用时试件内部自由水对抗压强度的减弱作用
自由水获得动能后对试件力学强度的减弱作用可以归纳为射流冲击、水击冲击这2种。
2.3.1 射流冲击对试件力学性能的影响
高速流动的自由水在试件内部会产生射流冲击现象,其主要发生在分叉圆柱管的入口、出口处(图4)。
(1)分叉圆柱管网入口处的射流冲击
图5为图4中区域入口处的局部分析,作出如下假设:1)自由水密度是常数;2)自由水为恒定流动;3)过流断面为渐变流断面;4)忽略自由水流动中的机械能损失。
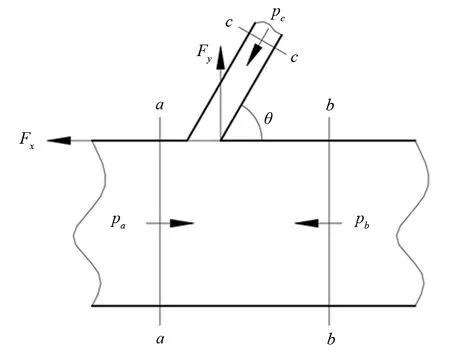
a、b、c为截面;θ为分叉管倾角(°);pa为截面a处压力(MPa);pb为截面b处压力(MPa);pc为截面c处压力(MPa);Fx为导管壁对自由水沿x方向的作用力(N);Fy为导管壁对自由水沿y方向的作用力(N)。
取截面a、b处的圆柱管直径(da、db)均为57 μm,截面c处的圆柱管直径(dc)取杨木导管壁纹孔直径约为10 μm[18];截面a处自由水的流速(va)为试验中测得应变率1 000 s-1时,质点的速度约为20 m·s-1,截面b处的自由水的流速(vb)下降率为2.5%,截面a处的压强(Pa)为1 MPa[17]。由流体连续性方程可得截面c处自由水的流速(vc),公式为:
(2)
截面a、c,截面a、b的伯努利方程分别为:
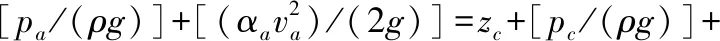
(3)
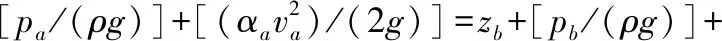
(4)
式中:za、zb、zc分别为截面a、b、c的高度;αa、αb、αc分别为截面a、b、c上的动能修正系数;g为重力系数(N·kg-1);ρ为自由水密度(kg·m-3);hla-c为自由水从截面a流到截面c过程中的能量损耗;hla-b为自由水从截面a流到截面b过程中的能量损耗。
总流动量方程的投影式为:
Fa-Fccosθ-Fb-Fx=(ρqbβbvb+ρqcβcvccosθ)-
ρqaβava。
(5)
Fcsinθ-Fy=ρqc(-βcvcsinθ)。
(6)
式中:Fa、Fb、Fc分别为截面a、b、c处自由水受到的作用力(N);qa、qb、qc分别为截面a、b、c处自由水的流量(m3·s-1);βa、βb、βc分别为截面a、b、c上的动量修正系数;
圆柱管中层流动能和动量修正系数均为1,取θ=60°,根据假设条件,由式(3)~(6)可得导管壁对自由水的作用力(F),公式为:
(7)
分叉圆柱管区域入口处自由水射流冲击对导管壁的作用力约为9.06×10-5N。因此,在加载过程中,分叉圆柱管入口处的射流现象对试件的破坏作用可以忽略不计。
(2)分叉圆柱管网出口处的射流冲击
图6为图4中区域出口处的局部分析,作出如下假设:1)分析区域内没有自由水,压强等于大气压,相对压强为0;2)圆柱管内壁对自由水没有阻碍作用。
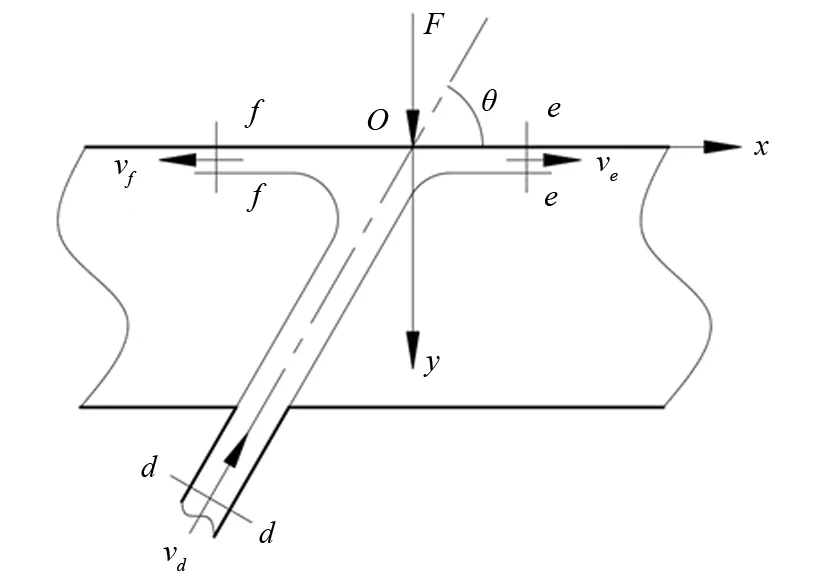
d、e、f为截面;vd为截面d处自由水的流速(m·s-1);ve为截面e处自由水的流速(m·s-1);vf为截面f处自由水的流速(m·s-1);θ为分叉管倾角(°);F为导管壁对自由水的作用力(N)。
圆管中层流动能修正系数αd=αe=αf=1,结合截面d、e,截面d、f的伯努利方程可知截面d、e、f的流速(vd、ve、vf)均相等。根据假设条件,列Ox方向上的动量方程为:
ρqeve-ρqfvf-ρqdvdcosθ=0。
(8)
根据流体连续性方程,结合式(8),可得截面e、f处自由水流量qe、qf分别为:
qe=0.5qd(1+cosθ)。
(9)
qf=0.5qd(1-cosθ)。
(10)
在区域出口处自由水冲击现象中,自由水流量只与冲击方向和壁面之间的夹角有关。对于圆柱管中层流动量修正系数(β)为1,由Oy方向上的动量方程可得圆柱管内壁对自由水的作用力(F)为:
F=ρqdvdsinθ。
(11)
分叉圆柱管区域出口处自由水对导管内壁的作用力为1.79×10-5N。因此,在加载过程中,分叉圆柱管出口处射流冲击对试件的破坏作用也可以忽略不计。
综上分析,试件内部自由水的射流冲击不会对试件的结构造成破坏,从而不会降低试件的强度。
2.3.2 水击冲击对试件力学性能的影响
自由水在试件内部流动时,会因为路径不通在试件内部产生水击冲击(图7)。
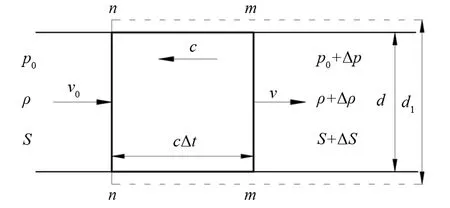
n、m为截面;c为水击波的传播速度(m·s-1);p0为水击波通过前截面n处的压力(MPa);ρ为水击波通过前截面n处的自由水密度(kg·m-3);S为截面n处导管的截面面积(m2);v0为水击波通过前自由水的流速(m·s-1);v为水击波通过后自由水流速(m·s-1);Δp为水击波通过后压力的增量(MPa);Δρ为水击波通过后自由水密度的增量(kg·m-3);ΔS为水击波通过后导管截面面积的增量(m2);Δt为水击波由截面m传至截面n的时间(s);d1水击波通过后导管的直径(m)。
根据质点系动量定理,可得:
[p0S-(p0+Δp)(S+ΔS)]Δt=(ρ+Δρ)(S+ΔS)cΔtv-
ρScΔtv0。
(12)
试验条件下自由水的压缩系数约为5.31×10-10m2·N-1,故Δρ远小于ρ,ΔS远小于S,则式(12)化简为:
Δp=ρc(v0-v)。
(13)
当自由水由于流动路径不通,速度(v)突然降为0时,式(13)得到水击冲击压强最大值:
Δp=ρcv0。
(14)
自由水密度(ρ)为1×103kg·m-3,初始流动速度(v0)为20 m·s-1,水击波传播速度(c)为1 001.79 m·s-1,试件内部自由水水击冲击产生的局部最大压强为20 MPa。
高应变率加载试验,测得应变率为1 000 s-1时杨木径向、弦向抗压强度分别约为9.27、7.25 MPa,水击冲击产生的最大局部压强分别约为径向、弦向抗压强度的2.16、2.76倍。因此,自由水局部水击冲击会对木材内部结构造成破坏,从而降低木材试件的强度。
2.4 高应变率作用时试件内部自由水对抗压强度的增强作用
自由水获得大量动能的同时也消耗掉了大量冲击功,变向增强了试件强度。试件内部自由水能量的消耗主要通过沿程和局部能量损耗两种方式。
2.4.1 沿程能量损耗
将木材试件内部自由水的流动简化为圆管内的层流,整个管流如同无数薄壁圆筒一个套着一个滑动(图8)。各流层间的切应力服从牛顿内摩擦定律,公式为:
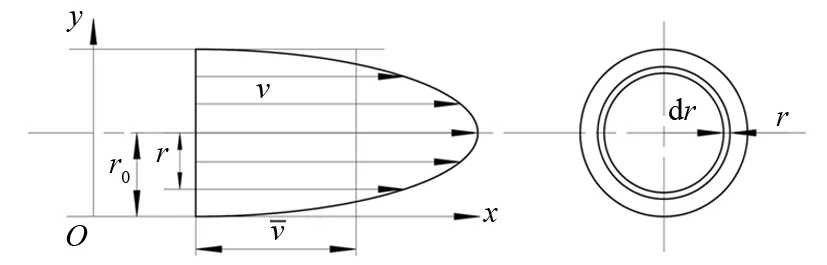
r为研究对象流束半径(m);r0为导管半径(m);v为自由水流速为自由水平均流速(m·s-1)。
τ=-μ·(dv/dr)。
(15)
式中:τ为流束表面的切应力(Pa);μ为自由水粘度(Pa·s)。
圆管过流截面上流束均匀流动方程为:
τ=(ρgrJ)/2。
(16)
式中:J为流束的水力坡度(°)。
将式(15)代入式(16)中,分离变量并积分可得:
v=-(ρgJr2)/(4μ)+η。
(17)
式中:η为积分常数。
将边界条件r=r0、v=0,代入式(17)并整理得到自由水在试件内部流动时,过流截面上的流速分布方程:
(18)
(19)
将r0=d/2和J=hf/l代入式(19)并整理,得到试件内部自由水流动过程中的沿程能量损耗(hf)为:
(20)
式中:l为研究对象流速长度(m);λ为圆管层流的沿程阻力系数。
可知,木材试件内部自由水的流动路径越长、内径越小、流速越高,流动过程中消耗的能量越大。
2.4.2 局部能量损耗
根据试件内部自由水的流动路径,将自由水流动的局部能量损耗分为扩大管、缩小管(图9)。
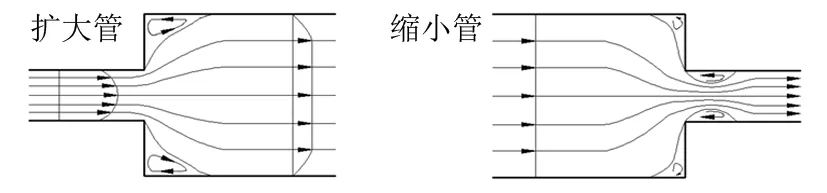
图9 局部能量损耗示意图
局部能量损耗(hm)的计算公式为:
(21)
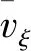
由式(21)可知,局部能量损耗与局部阻力系数(ξ)成正比,与截面平均流速的二次方成正比,木材试件内部流动路径截面变化越显著,自由水流速越高,流动过程中消耗的能量越大。
综上所述,高应变率加载条件时,自由水对木材强度既起到增强作用又起到减弱作用,增强和减弱作用耦合在一起,最终表现为增强还是减弱作用主要受加载应变率的影响。自由水对木材强度的影响可表达为:
(22)
(23)
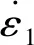
当加载应变率满足式(22)时,自由水主要起增强试件强度的作用;当加载应变率满足式(23)时,自由水主要起减弱试件强度的作用。最小应变率和临界应变率的大小受试材密度、孔隙度等影响,相当于一种材料属性。
3 结论
全饱和试件的解离程度随应变率的增加而增加,抗压强度具有明显的应变率效应。
全饱和试件内部的自由水可以自由流动,自由水流动的雷诺数为1 127.60,流态为层流,自由水获得的动能大小与加载应变率成正比。自由水的射流冲击不会对试件强度产生影响,但水击冲击产生的最大局部压强分别约为径向、弦向抗压强度的2.16、2.76倍,会破坏试件内部结构,进而降低试件强度。自由水通过沿程、局部能量损耗消耗掉冲击功,起到增强试件强度的作用。
自由水对试件强度的增强与减弱作用主要受应变率的影响,当应变率小于临界应变率时,自由水主要起增强木材强度的作用;当应变率大于临界应变率时,自由水主要起减弱木材强度的作用。
在纤维板实际生产中木材原料的应变率和热磨机的转速成正比,改变热磨机的转速可改变木材原料的应变率[19]。当木材原料的应变率大于临界应变率时,木材原料的解离强度随热磨机转速的增加而减小,由此合理确定热磨机的转速可减少研磨过程中的能量消耗,这对制备纤维的关键设备,各种类型热磨机转速的设计提供了理论依据。

