阵列式阻性消声器传递损失计算模型*

赵亚林 蒋浩杰 马建刚 王 绿 方庆川 翟国庆

(1 国网陕西省电力有限公司电力科学研究院 西安 710100)

(2 浙江大学环境与资源学院 杭州 310058)

(3 深圳中雅机电实业有限公司 深圳 518031)

0 引言

阵列式阻性消声器是近年来一种非常有潜力的新型消声器[1]。与片式阻性消声器相比，阵列式消声器吸声柱宽度和总吸声面积较大，具有更高消声量，且具有通流面积大、气流阻力小、气流再生噪声和压力损失小等优点[2]，在大风量的地铁风亭、空冷器、冷却塔和航空发动机试车间等场所得到广泛应用[3-4]。

消声器消声量通常采用传递损失(Transmission loss,TL)进行评价。TL 指消声器入口端声功率级和出口端声功率级的差值，其可通过测量或理论计算确定。阵列式消声器几何尺寸通常较大，《声学 管道消声器和风道末端单元的实验室测量方法插入损失、气流噪声和全压损失》(GB/T 25516–2010)中给出的常规试验台无法满足其测试要求。为此，《声学 单元并排式阻性消声器传声损失、气流再生噪声和全压损失系数的测定等效法》(GB/T 36079–2018)提出采用等效法测量阵列式消声器消声量，该方法需测量断面参数完全相同但长度不等的2 台消声器，根据测试结果确定阵列式消声器单位长度消声量，消声量测量费时费力且投入大，有必要发展阵列式消声器消声量计算模型。阻性消声器消声量计算公式主要有Belov 公式和Sabine公式[5-6]。Belov在声波导管理论基础上，假设导管壁面为非刚性壁面且导管截面尺寸较小，推导了适用于直管式消声器的消声量计算公式[7-9]。Sabine 建立了实际管道系统，通过测量不同长度、尺寸和形状的管道中声衰减量，根据实验数据总结出直管式消声器消声量计算公式[10-11]。Belov 公式和Sabine 公式均针对单通道的直管式阻性消声器，不适用于横截面尺寸较大且气流通道彼此连通的阵列式阻性消声器。

本文根据阵列式消声器结构特点，在合理划分消声单元基础上，建立了半理论半经验消声量计算模型，并采用实测数据对模型进行了验证。

1 阵列式消声器消声量计算模型构建方法

阵列式阻性消声器由吸声柱、外壳、支架杆组成，吸声柱在垂直气流断面上呈阵列式分布，吸声柱两端装有导流罩，吸声柱横截面通常为矩形。阵列式阻性消声器结构示意图见图1。

图1 阵列式阻性消声器结构示意Fig.1 Schematic diagram of the structure of arrayed element dissipative silencer

图1 中，W为消声器宽度；H为消声器高度；L为消声器有效长度；a为矩形吸声柱横截面长度；a′为矩形吸声柱横截面宽度；b为吸声柱横向柱间距；b′为吸声柱纵向柱间距；b/2 和b′/2 分别为吸声柱与外壳的横向间距和纵向间距，其通常为柱间距的1/2。

m×n阵列式阻性消声器含有m×n个吸声柱，将其划分为m×n个周期性排列的消声单元(见图1中红色框)，每个消声单元包含1 个吸声柱。阵列式消声器具有周期性结构，可以将单个消声单元的消声量视为阵列式消声器消声量。每个消声单元的倍频带消声量理论值TLt为抗性部分(进出口气流通道截面突变处)倍频带消声量理论值TL1和阻性部分倍频带消声量理论值TL2之和：

将抗性部分等效为扩张式消声器，计算其每个频率上的消声量理论值。对第i个倍频带，其频率范围记为[fi,a,fi,b]，中心频率为fi。对闭区间[fi,a,fi,b]做n等分，获得n个子区间[x0,x1]、[x1,x2]、···、[xn-1,xn]，取每个子区间的频率中值，记作f0、f1、···、fn-1。根据黎曼积分定义计算抗性部分第i个倍频带消声量理论值TL1,i，

式(2)中，M为消声单元扩张比，

L为消声器有效长度；k为波数，k=2π/λ。

阻性部分倍频带消声量理论值TL2采用Belov公式计算：

式(3)中，φ(α0)为消声系数；α0为吸声材料垂直入射吸声系数；P为消声单元中吸声柱横截面周长，P=2(a+a′)；L为消声单元有效消声长度；S为消声单元有效通风面积，

根据《工业企业噪声控制设计规范》(GB/T 50087–2003)给出的垂直入射吸声系数与消声系数换算表可确定消声系数φ(α0)和吸声系数α0换算关系：

本研究使用Delany-Bazley-Miki模型对阵列式阻性消声器采用的多孔吸声材料进行表征，吸声材料的垂直入射吸声系数计算见公式(5)。其中，表面声阻抗Zs、特征声阻抗Zc和传播常数Kc见公式(6)、公式(7)和公式(8)。

其中，α0为吸声材料垂直入射吸声系数；σ为材料流阻率；ρ0、c0、f和ω分别为空气密度、空气中的声速、声波频率和角频率；d为多孔材料厚度，d=0.5(a+a′)。

消声器气流通道截面较大时，随着入射声波频率增高，声波逐渐呈声束状传播，与吸声材料很少或不完全接触，入射至吸声材料处的声能量明显下降，这种现象称为高频失效。常见阻性消声器高频失效修正见公式(9)，高频失效频率计算见公式(10)[5]：

阻性消声器高频失效频率与气流通道横截面形状和尺寸有关。阵列式阻性消声器各消声单元彼此连通，气流通道横截面呈异形且等效尺寸较大，无法利用公式(10)计算气流通道的高频失效频率，且公式(9)只能用于修正大于fu的3 个倍频带消声量。为此，本研究拟参考公式(9)在各倍频带引入消声量修正系数β，对阻性部分各倍频带消声量理论值进行修正。通过拟合各倍频带修正系数得到倍频带修正函数Nf。引入倍频带修正函数Nf后阻性部分倍频带消声量理论值见公式(11)：

根据公式(12)，可得到倍频带修正函数Nf的表达式，见公式(13)：

为确定不同吸声材料对应的倍频带修正函数Nf，需对阵列式消声器倍频带消声量理论值进行仿真。采用有限元法仿真计算阵列式消声器每个频率下的消声量，通过拟合可建立消声量仿真值TLs和f的关系函数TL(f)。根据黎曼积分定义计算第i个倍频带消声量仿真值TLs,i(见公式(14))。将各倍频带消声仿真结果TLs代替代入公式(13)，可得到阵列式消声器阻性部分消声量倍频带修正函数Nf。

2 算例分析

根据前面所述阵列式消声器消声量计算模型构建方法，当多孔吸声材料流阻率不同时，阵列式消声器阻性部分消声量倍频带修正函数Nf会有所不同。本研究以流阻率为11425 Pa·s/m2的多孔吸声材料为例，建立了适用于不同结构尺寸的阵列式消声器消声量计算模型。

2.1 消声量仿真计算

2.1.1 建立几何模型

阵列式消声器具有周期性结构，将单个消声单元消声量视为阵列式消声器消声量，即忽略吸声柱数量对消声量的影响，不妨m取5，n取5。工程上所采用的阵列式阻性消声器吸声柱横截面通常为矩形，消声器通流比(有效通风截面与消声器横截面面积之比)大于0.5，吸声柱横截面长度和宽度通常取100～500 mm，相邻两个吸声柱间距常取50～500 mm。为此，本研究选取3 种典型吸声柱，其横截面尺寸分别为100 mm×100 mm、200 mm×200 mm和300 mm×300 mm，3种典型消声器柱间距分别为100 mm、150 mm和200 mm。由于消声量与消声器长度成正比，故消声器长度均取1000 mm。采用多物理场仿真软件建立3 种典型阵列式消声器模型，其结构参数见表1，仿真模型见图2。

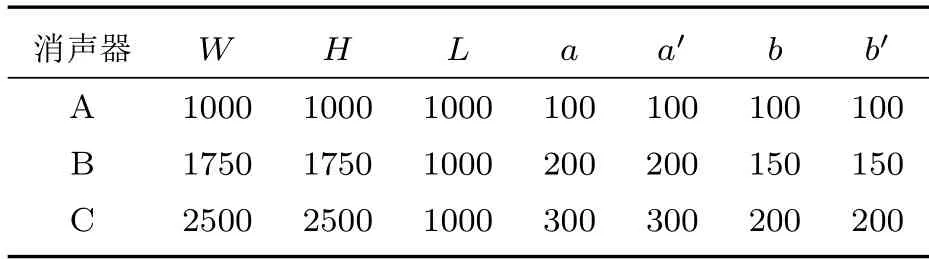
表1 阵列式消声器模型结构参数Table 1 Structural parameters of arrayed element dissipative silencer models(单位：mm)

图2 阵列式阻性消声器仿真模型Fig.2 Simulation model of arrayed elements dissipative silencer

2.1.2 定义材料属性

声学计算中使用Delany-Bazley-Miki 模型对多孔吸声材料进行表征，需要定义材料流阻率σ。本算例中，选取的多孔吸声材料流阻率为11425 Pa·s/m2。

2.1.3 物理场设置

仿真模型中空气域采用压力声学模块进行建模，吸声柱内部吸声材料采用多孔介质声学建模，模型两端最外侧空气域设为完美匹配层。消声器壁面设置为硬声场边界，吸声柱两端导流罩设置为内部硬声场边界。入射声场设置背景压力场，压力场类型为平面波，声压幅值为1 Pa，入射方向为垂直入射。当声源激发频率高于管道的截止频率，管道中会存在大量的高阶模态声波，此时管道内的声场是各个模态叠加的稳态声场。

2.1.4 网格划分

采用三棱柱单元对完美匹配层进行网格划分，气流垂直入射方向上网格层数设为8 层，其余区域均采用自由四面体单元划分网格。为保证求解精度，最大网格单元尺寸设为最小波长的1/8。本研究中仿真计算63～4000 Hz 各倍频带消声量，其频率上限为5600 Hz，故最大网格单元尺寸取5600 Hz对应波长的1/8。

2.2 仿真结果

垂直入射情况下，阵列式消声器各倍频带消声量仿真值TLs见表2。

表2 阵列式消声器消声量仿真值TLsTable 2 Simulated values,TLs of noise elimination of arrayed element dissipative silencers(单位：dB)

由表2 可知，阵列式消声器各倍频带消声量随着频率升高先增大后减小，在1000 Hz 倍频带上达到峰值。

本研究以Delany-Bazley-Miki 模型为理论基础，采用多物理场仿真软件建立多孔吸声材料等效模型，仿真计算流阻率为11425 Pa·s/m2，厚度为100 mm、200 mm 和300 mm 的多孔吸声材料垂直入射吸声系数。根据公式(4)计算多孔吸声材料消声系数(见表3)。

表3 吸声材料的消声系数Table 3 Anechoic coefficients of sound-absorbing materials

将各倍频带消声仿真结果TLs代替代入公式(13)，可计算得到各倍频带消声量修正系数，结果见表4。由表4 可知，不同阵列式消声器各倍频带消声量修正系数相近，故取算术平均值作为各倍频带消声量修正系数。

表4 阵列式消声器各倍频带消声量修正系数Table 4 Correction coefficients of noise elimination of arrayed element dissipative silencers at each 1/1 octave band

由表4 可知，各倍频带消声量修正系数随频率升高先增大后减小，在1000 Hz 处达到峰值，整体呈现中间高两边低的特点，类似高斯分布。采用高斯分布函数对各倍频带消声量修正系数进行拟合(见图3)，可得到倍频带修正函数Nf(见式(15))。

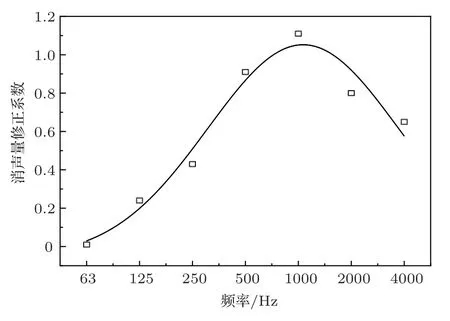
图3 倍频带消声量修正系数拟合曲线Fig.3 Fitting curve of correction coefficients of noise elimination at 1/1 octave band

式(15)中，fi为第i个倍频带中心频率。

综上，修正后的阵列式阻性消声器第i个倍频带消声量理论值计算模型见公式(16)。

3 实测验证

采用1×2阵列式消声器实测数据和文献[12]给出的2×2 阵列式消声器实测数据，对修正后的阵列式阻性消声器消声量计算模型进行验证，上述消声量均按GB/T 25516–2010标准进行测量，消声器结构参数见表5。修正后的消声量理论值和实测值见表6。

表5 验证用阵列式消声器结构参数Table 5 Structural parameters of arrayed element dissipative silencer models for verification(单位：mm)

表6 修正后的消声量理论值 和实测值Table 6 Modified theoretical values and measured values of noise elimination

表6 修正后的消声量理论值 和实测值Table 6 Modified theoretical values and measured values of noise elimination

4 结论

针对Belov 基于声波导管理论推导的阻性消声器消声量计算公式，不适用于气流通道彼此连通且截面尺寸较大的阵列式阻性消声器问题，本研究提出了一种阵列式消声器消声量计算方法。同时，以流阻率为11425 Pa·s/m2多孔吸声材料为例，建立了适用于不同结构尺寸的阵列式消声器消声量计算模型。实测结果验证表明，各倍频带修正后的消声量理论值与实测值绝对误差均小于3 dB。当吸声材料的流阻率与算例中取值相差较大时，消声量计算模型可参照本研究所述方法另行建立。可进一步研究吸声材料流阻率对各倍频带阻性消声量修正函数Nf的影响，通过在模型中增加与流阻率有关的消声量修正项，建立计算阵列式阻性消声器消声量的普适模型。