(2-RPU+UPU)+(RR)混联机构末端约束和运动耦合分析
胡 波 高 添 曾达幸 卢文娟 王 帅 王国永
(1.燕山大学机械工程学院, 秦皇岛 066000; 2.东莞理工学院机械工程学院, 东莞 523808;3.河北石油职业技术大学机械工程系, 承德 067000)
0 引言
混联机构是机器人机构的重要分支,其中以两转动一移动(2R1T)并联机构为重要组成部分的五自由度混联构型[1-6]备受工业界青睐,以其为本体的混联机器人得到了广泛的应用,典型成功案例包括Exechon[1-2]、 Tricept[3-4]、 Sprint Z3[5-6]混联机构等。这类机构中,Exechon机构由2-UPR+SPR型并联模块和RR型串联机构组成。该机构运动副数目少且机构中存在过约束,这些特点带来了整体机构精度和刚度等性能的提升。受Exechon机构启发,诸多学者提出了新的构型方案。李秦川等[7]提出了具有此类特点的含垂直交错转轴的2R1T机构,并综合出了大量新型RPR类并联机构构型[8],其中包括多种具有此类特点的并联机构。JIN等[9]提了以2-RPU+SPR机构为并联模块的可用于飞机机翼装配的五自由度混联机构。路曼等[10]研究了类Exechon机构构型综合、运动学和样机研制问题。胡波等[11]提出了2-RPU+UPU机构,并证明了包括2-RPU+UPU、2-RPU+UPR、2-RPU+SPR等在内的23种机构实际上为运动学完全等效的并联机构[12]。此类机构的研究也引起了其他学者的关注[13-14]。由于运动等效性质的存在,这23种并联机构和RR模块组成混联机构时,其末端约束和运动特性具有共性,只需以其中一种(2-RPU+UPU)+(RR)机构研究为例即可。实际上,由2-RPU+UPU机构和RR模块组成的混联机构的研究还并不完善。
在少自由度混联机构的机构分析方面,以往研究通常将混联机构分成独立并联机构和串联机构分别研究,认为整体混联机构的理论模型是独立机构的简单叠加,忽视了对整体混联机构理论建模的研究和分析。末端约束分析是少自由度混联机构分析的重要内容[15-18],是开展机构分析和综合的基础,针对串联机构和并联机构的约束分析一直是机构学的研究热点,并且其研究已经相当成熟。然而,针对混联机构的整机末端约束分析实际非常少见,仅见文献[17]分析了5自由度Exechon混联机构的整机末端约束。针对(2-RPU+UPU)+(RR)混联机构的末端约束分析尚未见报道。
末端运动耦合是少自由度机构的重要特性,与末端具有六自由度运动的机构不同,少自由度机构末端六维移动和转动参数之间存在着相互耦合关系,在计算反解过程中不能任意给定,必须首先通过体现末端位姿耦合关系的方程求解末端可行六维位姿参数。在这一问题的处理上,目前多结合伴随运动[19-20]的求解方式得到机构运动耦合关系。然而由于(2-RPU+UPU)+(RR)混联机构具有不同于传统并联机构的末端运动耦合形式,其末端运动耦合并未能妥善解决。
为解决(2-RPU+UPU)+(RR)混联机构中存在的末端约束和运动耦合问题,本文采用Grassmann-Cayley代数求解该机构的末端约束,并结合整体机构的约束方程,通过消元得到只含末端6维位姿参数的末端运动耦合模型,以期为(2-RPU+UPU)+(RR)机构提供解析化的末端约束和运动耦合模型。
1 (2-RPU+UPU)+(RR)机构末端约束分析
1.1 混联机构描述
如图1所示,混联机构由2-RPU+UPU型并联模块和RR型串联模块组成。2-RPU+UPU型并联模块由动平台n1、定平台n0、2条结构相同的RPU分支ri(i=1,3)和1条UPU分支r2组成。定平台n0和动平台n1均为三角形结构,其中心分别为p0和p1,端点分别记为ai和bi(i=1,2,3)。3条分支呈对称分布,并均将P副作为驱动副,RPU分支ri(i=1,3)通过R副与定平台n0上的ai(i=1,3)连接,并通过U副与动平台n1上的bi(i=1,3)连接,UPU分支r2通过U副与定平台n0上的a2连接,并通过U副与动平台n1上的b2连接。并联模块中的每个U副均由转轴相互垂直且相交的R副组成,设R1ij表示第i条分支上的第j个R副。

图1 (2-RPU+UPU)+(RR)型混联机构示意图Fig.1 Sketch of (2-RPU+UPU)+(RR) type hybrid mechanism
定义:并联模块中的各个运动副满足如下关系R1i1⊥a1a3,R1i1⊥ri,R1i1‖R1i2,R1i2⊥R1i3(i=1,2,3),R1i3|b1b3(i=1,3),R121|p0a2,R121⊥R122,R122‖R123,R123⊥ri,R123⊥R124,R124⊥n1。
RR型串联模块由刚性连杆d、R21和R22组成,连杆d始端与p1固连,末端点为p2,R21和R22相交于p2。串联模块中的两个运动副和连杆、平台满足几何关系d|R21,R21⊥n1, R21⊥R22。
1.2 混联机构末端耦合约束求解方法
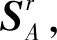
(1)
为解决式(1)的螺旋系求交问题,在此引入Grassmann-Cayley代数。Grassmann-Cayley代数是一个功能强大的数学工具,在并联机构/混联机构运动学和奇异性分析领域已有多个成功案例[21-22]。其交运算可应用于求解不同线性空间的交空间,可将其应用于两个螺旋系的求交运算。

C=w1∨w2∨…∨wk
(2)
在Grassmann-Cayley代数中,将C称为k阶extentor。
设M和N分别是两个l维空间内的i阶和j阶梯extensor,M=m1∨m2∨…∨mi(M=m1m2…mi),N=n1∨n2∨…∨nj(N=n1n2…nj)。M和N的求并运算可由其exterior product表示为
M∨N=m1m2…min1n2…nj
(3)
若i+j≥d,M和N的求交运算结果是一个i+j-d阶的extensor
M∧N=∑sgn(σ)[mσ(1)mσ(2)…mσ(d-j)n1n2…nj]·
mσ(d-j+1)mσ(d-j+2)…mσ(i)
(4)
式(4)为Grassmann-Cayley代数的混续积公式,其中[·]为行列式的简写,和运算是σ的所有排列组合,满足:σ(1)<σ(2)<…<σ(d-j),σ(d-j+1)<σ(d-j+2) <…<σ(i)。
1.3 (2-RPU+UPU)+(RR)机构末端约束及自由度
在点p0、p1、p2处分别建立坐标系{ni}(i=0, 1, 2),则{n0}和{n2}分别对应基坐标系和末端坐标系,各坐标轴满足的几何关系为:X0‖a1a3,Y0⊥a1a3,Z0⊥n0,X1‖b1b3,Y1⊥b1b3,Z1⊥n1,X2|R22。设pxi、pyi、pzi为点pi在基坐标系{n0}下的坐标。
由文献[12]知,该机构的第1、3分支中,存在一过U副中心平行于分支中R副的约束力FAi(i=1, 3)和垂直于U副平面的约束矩TAi,第2分支中存在过R121和R124交点c且平行于R122的约束力FA2。这5个约束螺旋线性相关,可取3个独立的约束力构成其约束螺旋系,3个约束力螺旋可表示为
(5)
其中
fAi=R1j1dAi=bi-p2(i=1,3)
fA2=R122dA2=c-p2
式中Rijk——转动副Rijk的方向矢量
bi、c、pi——点bi、c、pi的位置矢量
fAi——约束力FAi的方向矢量
dAi——参考点p2到FAi的矢径
同样,在RR分支中,由约束螺旋的观察法[15]知分支中存在过R副交点的3个约束力FBi(i=1,2,3)和一垂直于R21和R22的约束矩TB1,对应的力螺旋可表示为
(6)
由独立螺旋组成的螺旋系可通过各独立螺旋的外积运算表示[22],则2-RPU+UPU机构约束螺旋系可表示为
(7)
RR机构约束螺旋系可表示为
(8)
将式(7)、(8)代入式(4),则整体混联机构末端约束可表示为
(9)
式(9)为通过2个约束螺旋系求并运算得到的混联机构末端约束的解析表达式。
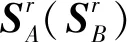
(10)
式中λAi、λBi——常数
2 (2-RPU+UPU)+(RR)机构末端运动耦合解析

(11)
末端坐标系{n2}相对于基坐标系{n0}的旋转变化可表示为
(12)
其中
(13)

点ai、bi在{n0}中可表示为
(14)
(15)

θ=π/6+(2π/3)(i-1)
式中E——点p0到点ai的长度
e——点p1到点bi的长度
2-RPU+UPU并联机构的杆长计算式为
ri=|bi-ai|
(16)
令pxi、pyi、pzi分别表示点pi在坐标系{n0}的3个坐标值。在基坐标系{n0}中p2可表示为
p2=p1+dZ1
(17)

2-RPU+UPU机构的末端位姿耦合关系可表示为[11]
px1=pz1zl1/zn1
(18)
py1=(eym1-E)/2
(19)
xm1=0
(20)
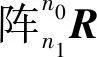
(21)
(22)
由式(17)可知(2-RPU+UPU)+(RR)混联机构的末端位置可表示为
px2=px1+dzl1
(23)
py2=py1+dzm1
(24)
pz2=pz1+dzn1
(25)
由该机构结构条件可知
zl1xl2+zm1xm2+zn1xn2=0
(26)
结合式(19)、(24),可得
py2=eym1/2+dzm1-E/2
(27)
结合式(20)、(21),可得
(28)
结合式(18)、(23)、(25),可得
(29)
由式(27)、(28)可得
(30)
由式(26)、 (29)可得
(31)
将式(29)、(31)代入式(22),化简可得
(32)
由式(31)、(32)可得
(33)
由式(30)可得
(34)
将式(33)代入式(34),两边平方,消去zm1,可得
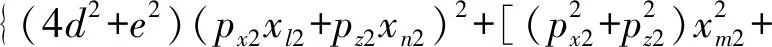
(35)
式(35)描述了5自由度(2-RPU+UPU)+(RR)混联机构的末端位姿耦合关系,当给定5个独立位姿参数时,剩余的1个位姿参数可由式(35)求出。
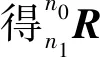
3 数值算例
设定(2RPU+UPU)+(RR)机构中,各平台及连杆的尺寸为E=1.20 m,e=0.60 m,d=0.75 m。给定末端执行器X和Z方向的位置坐标为:px2=-0.32 m,pz2=1.80 m,机构末端姿态按照XYX型欧拉角给定,对应欧拉角分别给定为:α=56°,β=-40°,λ=-80°,在给定以上5个位姿参数的基础上求解未知位置参数py2。
将上述参数代入式(35),可得到关于py2的高次方程为

(36)
式(36)求解可得py2为-0.792 5、0.099 7、-0.220 5、-0.472 3 m。
结果可在软件环境下构建机构的运动模拟机构得到验证[24]。结果表明仿真结果与式(36)计算结果的第2组结果吻合。
以上述得到的末端6维位姿参数为基础,(2-RPU+UPU)+(RR)机构的反解计算可得:r1=1.337 9 m,r2=1.148 0 m,r3=1.133 8 m,θ1=-35.201 2°,θ2=-4.579 9°。
在该位姿下,根据式(5)、(6)计算可得各子机构中的约束螺旋为

由式(9)计算可得该混联机构的末端约束为
Sr=[-0.403 8 0.912 0 -0.071 8 0.617 4 0.749 7 -0.204 4]T
结果表明,此位姿下(2-RPU+UPU)+(RR)机构的末端约束为以0.449 2 m为节距的约束螺旋。
4 结论
(1)得到了(2-RPU+UPU)+(RR)混联机构的末端约束和位姿耦合模型,为少自由度混联机构的整机末端约束和运动耦合分析提供了有效的思路和方法。
(2)基于约束求交原理,结合Grassmann-Cayley代数建立了(2-RPU+UPU)+(RR)混联机构的末端约束求解模型。在一般位形下,该机构的末端约束为一带有节距的约束螺旋,其末端自由度形式为2R2T1H型运动。
(3)结合(2-RPU+UPU)+(RR)混联机构的约束方程,通过消元建立了(2-RPU+UPU)+(RR)机构的末端运动耦合模型,从而获得了该机构的末端6维可行位姿,并以此得到了该机构修正的反向运动学模型。

