基于非匀质空间下Voronoi 图的城市影响范围研究

张晓贺

山西省测绘地理信息院，太原 030001

1 引 言

城市影响范围是城市在社会、经济、政治、文化等因素共同作用下对周围区域所及的最大地域范围（顾朝林等，1999)。确定城市影响范围，是城市规划的一项重要工作，有利于明确城市间的空间作用关系，促进城市合理布局。常用的城市影响范围研究方法有赖利模型、引力模型、潜力模型、断裂点模型、缓冲区分析、Voronoi 图（简称V 图)、加权V 图等。其中，赖利模型、引力模型、潜力模型、断裂点模型侧重理论分析，不能实现城市影响范围的具体划分（邓羽等，2013；常小刚和闫浩文，2015)；缓冲区分析不能对空间进行完全划分（黄杏元和徐寿成，1998)；V 图是对空间的一种完全划分，可以实现城市影响范围的具体划分（赵春燕等，2010；赵佳星等，2020)。

V 图生成算法可分为矢量和栅格两类。常用的矢量算法有分治算法、插入算法、扫描线算法等。矢量算法计算复杂，不利于海量数据的处理（李成名和陈军，1998)，且只能处理点和线段（Okabe 等，2000)。常见的栅格生成算法有扩张算法、距离变换算法、层次算法、细分算法、确定归属算法、光栅扫描算法（胡鹏等，2006)等。其中，综合考虑精度和效率因素，光栅扫描算法更具有优势，不需要考虑空间目标数量、分布和形状（Fabbri 等，2008)。传统光栅扫描算法，通过3×3（或者5×5)邻域模板在正反两次扫描中将一个栅格的信息传递给邻近的栅格，生成普通V 图（Chen，1999)。目前虽然有一些改进算法（Xu 等，2014；江威等，2015；刘青平等，2019)，但还不能满足非匀质空间和面状加权。李佳田等（2016)提出了非理想平面梯度V 图构建算法，只适合简单的点发生元；田松等（2014)基于结晶法提出了顾及障碍物的加权V 图算法，谢顺平等（2010)提出了一种基于网络分析的加权V 面域图构建算法，可以将交通路网纳入V 图的生成中，但都未扩展到整个非匀质空间。基于此，本文改进了光栅扫描算法，研究了非匀质空间下面状加权V 图的生成。以山西省11 个地级市为研究区，选取城市常住人口、辖区面积、国内生产总值（GDP)等18 项指标，采用主成分分析法构建了城市综合实力评价指标体系，用山西省坡度图构建非匀质空间，生成了其地级市影响范围图，并进行了对比分析。以期为促进山西省城镇科学规划提供参考。

2 非匀质空间面状加权V 图构建方法

2.1 方法原理

本文针对面状加权目标，改进了传统光栅扫描算法距离变换中的传递信息；针对非匀质空间，由于每个栅格像元传递权重不同，单个像元与目标点之间有众多不同传递权重的其他像元，其到目标点的最短路径会沿着传递权重最高的像元延伸，这样就导致最短路径不一定是直线，不能直接通过横纵坐标值来计算欧氏距离，所以本文按栅格像元传递权重对距离进行分解，用距离累加值代替传统的欧氏距离；为了提高归属精度，采用了“十字交叉”光栅扫描。

在光栅扫描的时候使用3×3 邻域模板（图1)，通过“十字交叉”4 次扫描实现距离变换，如图2所示：“左下—右上”纵向扫描时使用了模板（a)；“右上—左下”纵向扫描时使用了模板（b)；“左上—右下”横向扫描时使用了模板（c)；“右下—左上”横向扫描时使用了模板（d)。

图1 八邻域示意图Fig.1 8-neighborhood sketch

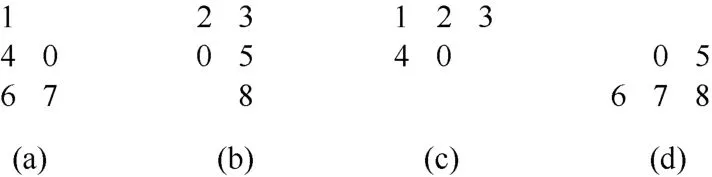
图2 扫描模板Fig.2 Scanning template

在距离变换的时候，所传递的信息为距离累加值最小时对应父结点行列号与最近目标点的行列号、目标编号、目标权重及距离累加值：

式中，为第n次扫描k邻域计算的距离累加值；Dk为k邻域传递过来的距离累加值；d为距离递增值，如图3 所示，四角取值，上下左右取值1；w1为k邻域传递过来的目标权重；w2为该栅格像元在非匀质空间中的传递权重。Dn为该栅格像元第n次扫描计算的最小距离累加值。

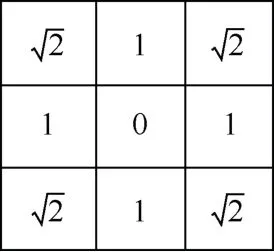
图3 距离递增图Fig.3 Incremental distance graph

四次交叉扫描结束后，连通最短路径生成非匀质空间下面状加权V 图。由于采用了光栅扫描方式，改进后的算法时间复杂度同样只受栅格化后像元数量的影响，不受目标数量、分布和形状的影响。

2.2 算法描述

输入：

（1)发生元，即面状目标矢量数据，按城市综合实力评价指标赋予权重；

（2)非匀质空间，即栅格传递权重图，本文按坡度对栅格赋予传递权重。

输出：非匀质空间下面状加权V 图。

算法：

（1)将面状目标和非匀质空间组合栅格化为M×N大小的3 通道图像，通道1 记录最近城市编号，通道2 记录最近城市权重，通道3 记录栅格所代表空间的传递权重；

（2)定义用于标注的结构体数组 mark T[M][N]{T.r，T.c，T.x，T.y，T.n，T.w，T.d}，分别记录父结点行列号（r，c)、最近目标点的行列号（x，y)、城市编号n、城市权重w，以及距离累加值d；

（3)“左下—右上”纵向扫描，按式（1)计算4 邻域传递过来的最小距离累加值，并用T[i][j]记录最小值对应父结点行列号与最近目标点的行列号、城市编号、城市权重，以及距离累加值；

（4)同步骤（3)继续完成“十字交叉”4 次扫描并连通最短路径；

（5)用T[M][N].n生成面状加权V 图。

3 城市综合实力评价指标体系

3.1 选择评价指标

城市综合实力评价是一个多维度的概念，因此要遵循全面性、可比性、可操作性等原则，选取不同角度的指标进行评价。如表1 所示，本文从城市规模水平、城市经济水平、社会发展水平、基础设施水平四个方面选取了18 项指标来构建山西省11个地级市评价指标体系，评价指标数据来自2020年《山西省统计年鉴》（山西省统计局，2020)。

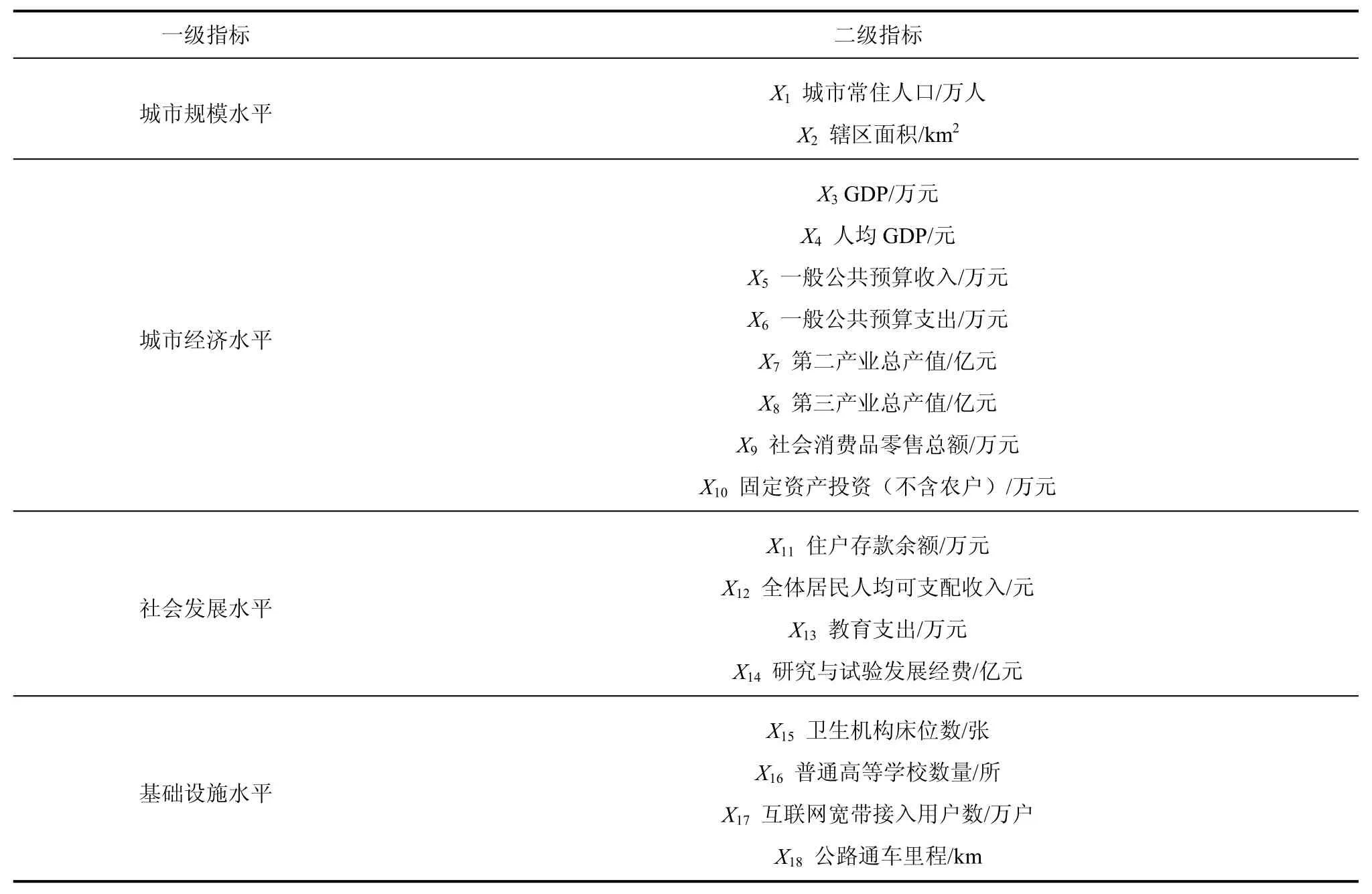
表1 城市综合实力评价指标体系Tab.1 Evaluation index system for urban comprehensive strength

3.2 数据处理

（1)标准化处理。对原始数据进行标准分数处理，首先计算数据的平均值和标准差，然后计算数据的标准化值。

（2)主成分分析。先通过正交变换将一组可能存在相关性的变量数据转换为一组线性不相关的变量，求得标准化后数据的协方差矩阵，计算特征值和相对应的特征向量；然后以主成分对总方差累计贡献率大于85%的标准提取n个主成分。由表2知，前两个因子的累计贡献率已达92.061%。

表2 总方差解释表Tab.2 Explanation of total variance

（3)求得11 个地级市的综合实力分数：

式中，Ak为第k个主成分贡献率；Pij为i市第j项指标的z-score 标准化值，Wj为指标j在主成分k上的得分系数。为了消除负值，便于后期V 图研究，利用式（2)对城市得分进行线性映射，映射区间[A，B]取值为[1，10]，计算结果作为城市权重，如表3所示。其中：

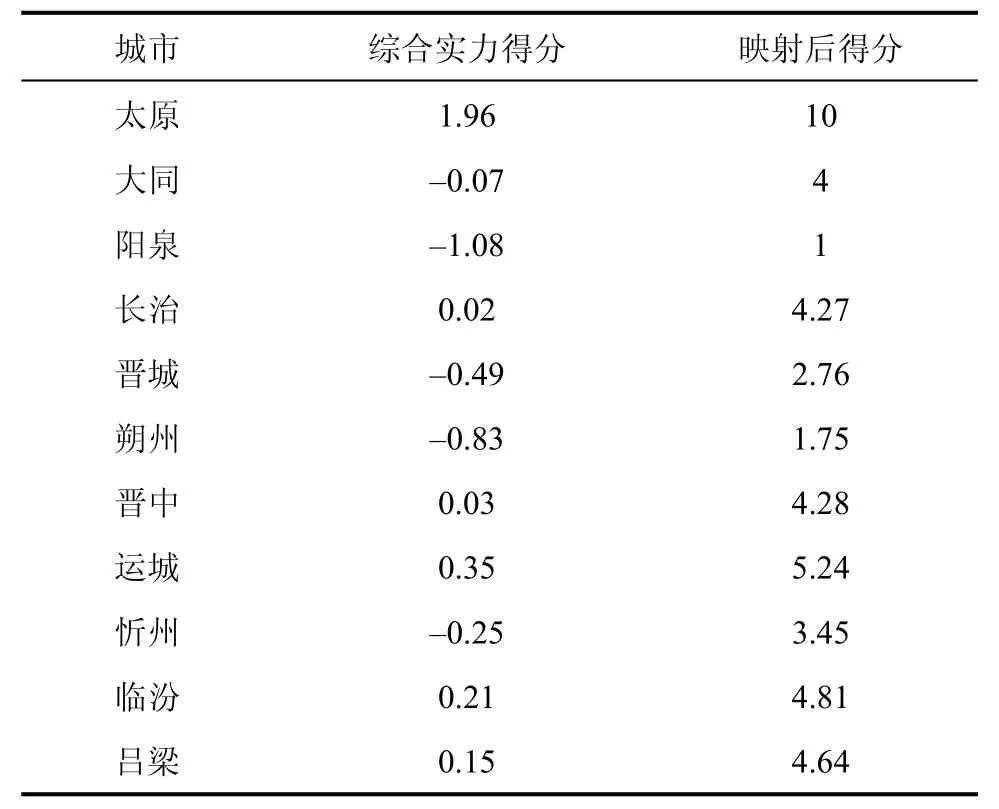
表3 城市综合实力最终得分Tab.3 Final score for urban comprehensive strength

式中，A为映射区间最小值；B为映射区间最大值。

4 山西省城市影响范围

以2021 年山西省11 个地级市建城区范围作为V 图的发生元，并将表3 中映射后得分作为影响权重赋予相应的发生元；因为城市影响主要通过人类活动实现，而人类活动会受地形影响，坡度越大，人类活动越受限制，即栅格像元的传递能力和坡度成反比，所以取山西省坡度图作为构建非匀质空间要素，按照式（4)给每个栅格像元赋予传递权重，坡度线性映射区间[A，B]取值为[1，50]：

式中，w2i为栅格像元i的传递权重；Gi为栅格像元对应的坡度值（°)；A为映射区间最小值；B为映射区间最大值。其中，山西省坡度区间为 0°～45.264°，如图4 所示。

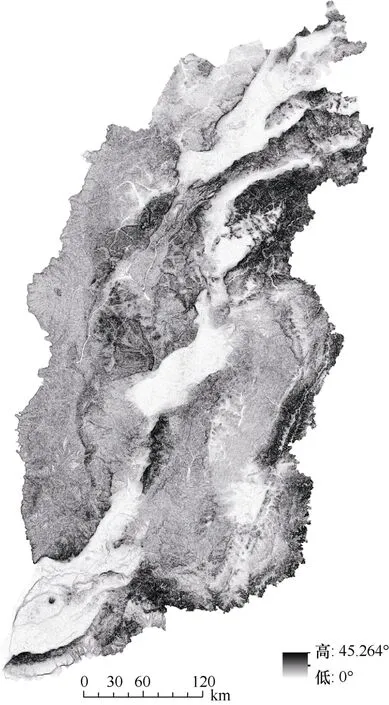
图4 山西省坡度图Fig.4 Slope map of Shanxi Province

以改进后的面状加权V 图算法为基础，利用ArcEngine 开发相应模块，生成山西省11 个地级市影响范围图。作为对比，匀质空间下取欧氏距离，分别构建点状和面状加权V 图。

如图5 所示，通过生成的V 图分析，总体上，太原作为省会城市，位于山西省中部，行政和区位优势得天独厚，其综合水平名列榜首，影响范围几乎囊括了整个山西省中部；运城、临汾、长治得分区别不大，占据了晋南大部分地区，晋城得分相对较低，划分影响范围相对较小；大同得分虽然不高，但由于独处晋北，影响范围囊括了整个山西北部，添加地形因素后，划分的影响范围增大；忻州、朔州、阳泉、晋中、吕梁影响范围受限于太原，尤其是晋中得分虽然比大同高，但因为离太原较近，其影响范围要远小于大同；添加地形因素后，由于山脉阻隔，朔州和忻州划分的影响范围增大。

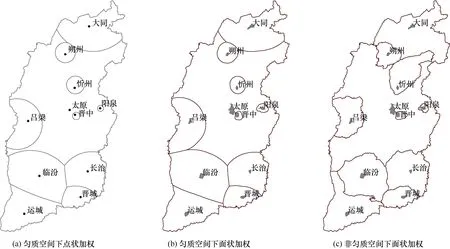
图5 山西省城市影响范围V 图Fig.5 Influence range map of cities in Shanxi Province

叠加对比图5（a)、（b)，点状加权V 图（呈弧形)不仅不能准确反映城市范围特征，且会将权重小的城市（阳泉、晋中)凸出区域划分到权重大的城市（太原)影响范围内（图6 中点状加权V 错分区域)，可见当城市之间权重差异较大、距离较近时，面状加权V 图（呈不规则线段)比点状加权V图更能精确划分城市影响范围；结合图4，对比图5（b)、（c)，山西省山区较多，均质空间加权V 图不能反映地形特点，非匀质空间加权V 图沿地形分布，城市影响范围划分受地形因素影响较大，尤其是在太原与忻州V 图边界的划分上表现比较明显，可见非匀质空间加权V 图更贴近实际。

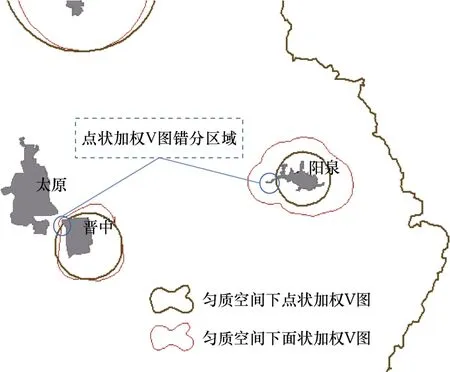
图6 点状加权V 图与面状加权V 图局部对比Fig.6 Local comparison between point-weighted Voronoi diagram and area-weighted Voronoi diagram

5 结 论

本文通过对V 图算法的研究，改进了光栅扫描算法，实现了非匀质空间下面状加权V 图的生成。以山西省11 个地级市为研究对象，选取了18 项指标，采用主成分分析法构建了城市综合实力评价指标体系，用山西省坡度图构建了非匀质空间，对山西省城市影响范围进行了研究。研究表明：

（1)山西省地级市影响范围呈现中心省会超强，南北相对均衡的特点；

（2)相比点状加权V 图，城市之间权重差异较大、距离较近时，面状加权V 图更适合城市影响范围划分。

如何科学确定评价指标计算城市综合得分确定城市权重，以及如何改进非匀质空间下V 图生成算法，提高边界精度等问题还有待进一步研究。