基于耐震时程法的浅埋压力箱涵结构抗震分析

宋 宸，任旭华，张继勋，项 勋

(河海大学水利水电学院，江苏 南京 210024)

0 引 言

目前我国建造了许多引水工程且较多采用浅埋的方式，而在地震多发地区，为保证引水工程的正常运行，结构的抗震性能尤其值得关注[1]。在地震作用下常用的结构响应计算方法有时程分析法和动力增量法等，采用这些常规方法对结构进行抗震计算时常面临着计算效率低的问题，对于复杂非线性接触问题计算收敛难度增加。耐震时程分析(ETA)法[2]通过1次计算就能够得到结构在不同强度地震下的动力响应，显著提高了结构抗震分析的计算效率。白久林等[3]通过对钢筋混凝土框架结构的抗震研究，验证了耐震时程法对结构抗震响应具有较好的预测能力。钟紫蓝等[4]建立土-地下结构相互作用的有限元模型，对比动力增量分析法，验证了耐震时程分析方法的高效性。在水工建筑物方面，徐强等[5]运用耐震时程法研究了强震作用下混凝土重力坝的损伤情况；此外，耐震时程法在特高拱坝[6]和沥青混凝土心墙砂砾石坝[7]等领域也有所应用。

现有浅埋地下结构抗震分析多为交通洞[8]，且多采用动力增量法[9]。黄仲凯等[10]研究了软土地层浅埋隧道的抗震易损性；王涛等[11]研究了装配式箱涵在不同埋深、不同地震动峰值加速度以及不同箱涵顶板伸出长度情况下箱涵的地震响应特征。为此，本文建立了考虑混凝土压力箱涵与周围土体接触非线性的浅埋压力箱涵有限元分析模型，采用耐震时程法分析其在不同工况不同持时下的位移、变形、损伤体积比、损伤耗散能及塑性耗散能等动力响应情况，并根据其损伤情况对其进行抗震性能评估，可为类似浅埋工程抗震研究提供参考。

1 基本原理与方法

1.1 耐震时程法

与常规时程分析方法相比，耐震时程法通过输入1条随时间不断增大的加速度时程曲线，表达结构在承受不同地震强度作用下的动力响应，通过1次计算便能够反映结构从弹性到塑性再到完全损伤的全过程。该方法所生成的耐震时程曲线的地震强度随着时间的增加逐渐增大，且在各个时程下，目标加速度反应谱与持时t呈线性关系，表达式如下

(1)

式中，tTarg et为目标时间；t为任意时间点；T为结构自振周期；SaC(T)为目标加速度反应谱；SaT(T，t)为时刻t的耐震时程曲线加速度反应谱。目标位移反应谱与其加速度反应谱具有相似关系，可表示为

(2)

式中，SuT(T，t)为时刻t的耐震时程曲线位移反应谱。

从耐震时程法的基本概念可以得知，耐震时程曲线在任意t时刻都需满足式(1)和式(2)，因此在一定精度允许的条件下可以将其转化为无约束优化问题，即

(3)

式中，ag为耐震时程加速度曲线；Tmax为反应谱最大周期；tmax为时程曲线最大持时；Sa(T，t)和Su(T，t)分别为计算所得0～t时的加速度反应谱和位移反应谱；α为位移谱权重系数，本研究仅考虑加速度反应谱，因此取α值为0。

1.2 生成耐震时程曲线

基于上述理论方法，参照GB 51247—2018《水工建筑物抗震设计标准》，选取规范中标准反应谱为目标谱，取目标反应谱最大代表值βmax=2.25，目标时间tTarg et=10 s，阻尼比5%，场地特征周期Tg=0.35 s为基本参数，生成3条初始人工地震动时程曲线。以该地震动作为初始输入，采用最小二乘法对上述生成的3条加速度时程曲线进行优化，得到了3条(ETA1～ETA3)总持时为40 s的耐震时程加速度曲线，见图1、2。从图1、2可知，计算的反应谱与标准目标谱较为吻合，不同时长的时程曲线峰值加速度分别对应为0.15g、0.30g、0.45g和0.60g。

图1 耐震时程加速度曲线

图2 耐震时程加速度反应谱曲线

1.3 地震动的输入

本文将黏弹性人工边界引入到压力箱涵结构抗震计算中，通过在模型的四周及底部施加黏弹性边界[12]实现模型对地震波的吸收和边界变形恢复的效果。采用将地震动转换为模型边界节点上等效节点力的方式来模拟地震动的输入[13]，其等效节点力可由下式计算

(4)

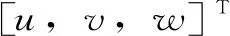
2 工程实例

2.1 计算模型

以某浅埋输水压力箱涵为例，该箱涵结构采用现浇双孔钢筋混凝土箱涵(单孔净宽×净高为3.4 m×4.0 m)，板厚500 mm，箱涵横向配筋Φ25@100～Φ16/18@200，纵向构造配筋内外侧均为Φ16@200。场地岩性主要为黏性土层。模型取1节箱涵的长度为13 m，箱涵两侧各延伸30 m，箱涵底部向下20 m，上部覆土约3.2 m，共有31 072个节点，网格27 180个。箱涵与土体相互作用的非线性三维有限元分析模型见图3。

图3 有限元模型

2.2 计算参数及本构模型

根据工程地质以及箱涵结构情况确定模型相关材料，具体参数见表1。按照规范要求，混凝土的动态弹性模量较静态弹性模量提高50%，动态抗拉强度取其动态抗压强度的10%，压力箱涵采用C30混凝土，其密度ρc=2 410 kg/m3，静态弹性模量Ec1=3.0×1010N/m2，动态弹性模量Ec2=4.5×1010N/m2，垫层采用C10混凝土材料。为考虑钢筋在压力箱涵中的作用并简化计算模型，采用钢筋混凝土的等效弹性模量和密度表示[14]，钢筋采用HRB400级钢筋，密度ρs=7 850 kg/m3，弹性模量Es=2.0×1011N/m2，泊松比μs=0.3。经计算，箱涵等效密度ρcs=2 489 kg/m3，静态等效弹性模量Ecs1=3.28×1010N/m2，动态等效弹性模量Ecs2=4.76×1010N/m2。

表1 相关材料物理力学参数

箱涵主体及垫层采用ABAQUS中混凝土塑性损伤模型(CDP)[15]模拟其损伤行为，模型土体采用弹塑性摩尔-库伦模型，混凝土的应力应变关系曲线及其损伤因子依据GB 50010—2010《混凝土结构设计规范》确定。CDP模型其他参数见表2。

表2 CDP模型材料参数

本文考虑压力箱涵有内水压力和无内水压力2种计算工况。2种工况均取模型上部均布荷载0.1 MPa，内水压力为0.2 MPa。在地震反应分析时，箱涵内部动水压力采用附加质量法施加。

3 计算结果分析

3.1 箱涵最大相对位移

在耐震时程的输入下，结构的位移响应往往是往复滞回的，因此在对压力箱涵位移进行分析时可依据下式将耐震时程法的分析结果进行处理，即

fEDP(t)=max(Abs(fEDP(τ)，τ∈[0，t]))

(6)

式中，fEDP(t)为t时刻的工程需求参数；fEDP(τ)为0～t时间段内结构的动力响应。

根据式(1)可获得箱涵在耐震时程计算下相对地基累计最大位移及3条耐震时程曲线计算结果的平均值，见图4、5。从图4、5可以看出，随着地震强度不断增大，2种工况下箱涵在竖向和侧向的累计位移曲线都呈现逐渐增大的趋势，且3条耐震时程曲线所计算的位移较为接近。在压力箱涵有内水压力时，随着峰值加速度的增大，相对于无内水压力时，其竖向位移有些许增大，侧向位移2工况下较为接近。其竖向最大相对累计位移均值约为0.11 m，侧向最大相对累计位移均值约为0.26 m，在地震动作用下，浅埋压力箱涵更易发生较大的侧向偏移。

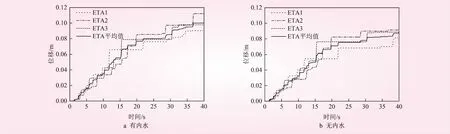
图4 箱涵竖向累计最大位移

图5 箱涵侧向累计最大位移

箱涵顶板相对底板竖向变形见图6，箱涵外侧墙相对中墙侧向变形见图7。从图6、7可知：

图6 箱涵顶板相对底板竖向变形

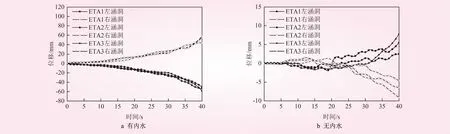
图7 箱涵外侧墙相对中墙侧向变形

(1)在ETA曲线处于0～10 s内时，对应的最大峰值强度约为0.15g，在箱涵有内水压力的情况下，箱涵结构顶板相对底板的残余变形可忽略不计，从第10 s左右开始，箱涵顶板相对底板的竖向残余变形开始呈现随时间增长而逐渐向上快速增大的趋势，最大值为94 mm。箱涵内部无内水压力时，前5 s内箱涵顶板相对底板的残余变形较小，从第5 s开始，箱涵顶板首先呈现出向下的相对残余变形，从第20 s开始，箱涵顶板相对底板的残余变形开始向上增大，最大值为16 mm。

(2)在有压状态下，箱涵外侧墙相对中墙的侧向残余变形在整个周期内呈现缓慢向外增大趋势，最大变形值为59 mm。前5 s内箱涵侧墙残余变形较小，从第5 s开始外侧墙呈现向内变形的趋势，从第15 s开始，箱涵外侧墙的相对残余变形逐渐转变为向外，最大值为9 mm。

(3)3条耐震曲线所计算得到的箱涵各残余变形趋势及结果都较为接近，有压状态下箱涵顶板的变形程度远大于无压状态，且顶板相对底板的残余变形要大于侧墙相对于中墙的变形。

左右涵洞顶板相对底板竖向残余变形差见图8。左右涵洞外侧墙相对中墙侧向残余变形差见图9。从图8、9可知，在3条不同耐震曲线所计算出的结果中，2种工况下箱涵左右两涵洞在相同持时下的残余变形相差不大，大部分误差在3 mm以内，两涵洞并不会产生较为明显的变形差异。其中，箱涵左右两涵洞顶板相对底板的竖向最大残余变形差发生在无内水压力工况下，相差4.33 mm；箱涵左右两涵洞外侧墙相对中墙的侧向最大残余变形差发生在有内水压力工况下，相差9.67 mm。

图8 左右涵洞顶板相对底板竖向残余变形差

图9 左右涵洞外侧墙相对中墙侧向残余变形差

3.2 箱涵动力损伤分析

箱涵结构的损伤体积能够定量反映压力箱涵在不同持时下的损伤程度。在结构的损伤裂缝发展过程中，其释放的断裂能为塑性耗散能与损伤耗散能之和，通过结构的损伤耗散便可以获得结构的裂缝发展情况[16]。因此引入损伤体积比(DVR)[17]、塑性耗散能和损伤耗散能作为响应指标对箱涵进行动力损伤分析。损伤体积比计算公式为

(7)

式中，n为单元数目；i为箱涵单元编号；di(t)为i号单元在t时刻下的损伤因子；Vi为i号单元的体积。塑性耗散能、损伤耗散能具体计算公式为

(8)

(9)

式中，MD为损伤耗散能；MP为塑性耗散能；σ为应力；εck为开裂应变；εpl为塑性应变。

图10为压力箱涵在不同持时下的受拉和受压损伤体积比。从图10可以看出，3条ETA曲线计算下箱涵的损伤体积比随持时增长呈现逐渐增大的趋势，且有内水压力工况下箱涵损伤体积大于无内水压力工况。在40 s对应峰值加速度0.6g时达到最大受拉损伤体积比约为0.64；2种工况箱涵受压损伤体积较小，因此不对箱涵受压损伤分布进行研究分析。

图10 箱涵损伤体积比

图11为塑性耗散能和损伤耗散能在整个时程内的变化。从图11可以看出，3条ETA曲线计算下箱涵的能量损失都较为接近，与结构的损伤变化情况相一致，有内水压力工况下的耗散能较无内水工况下更高。

图11 能量指标

图12、13为ETA2不同持时下压力箱涵有内水压和无内水压工况下的受拉损伤分布。从图中可知：

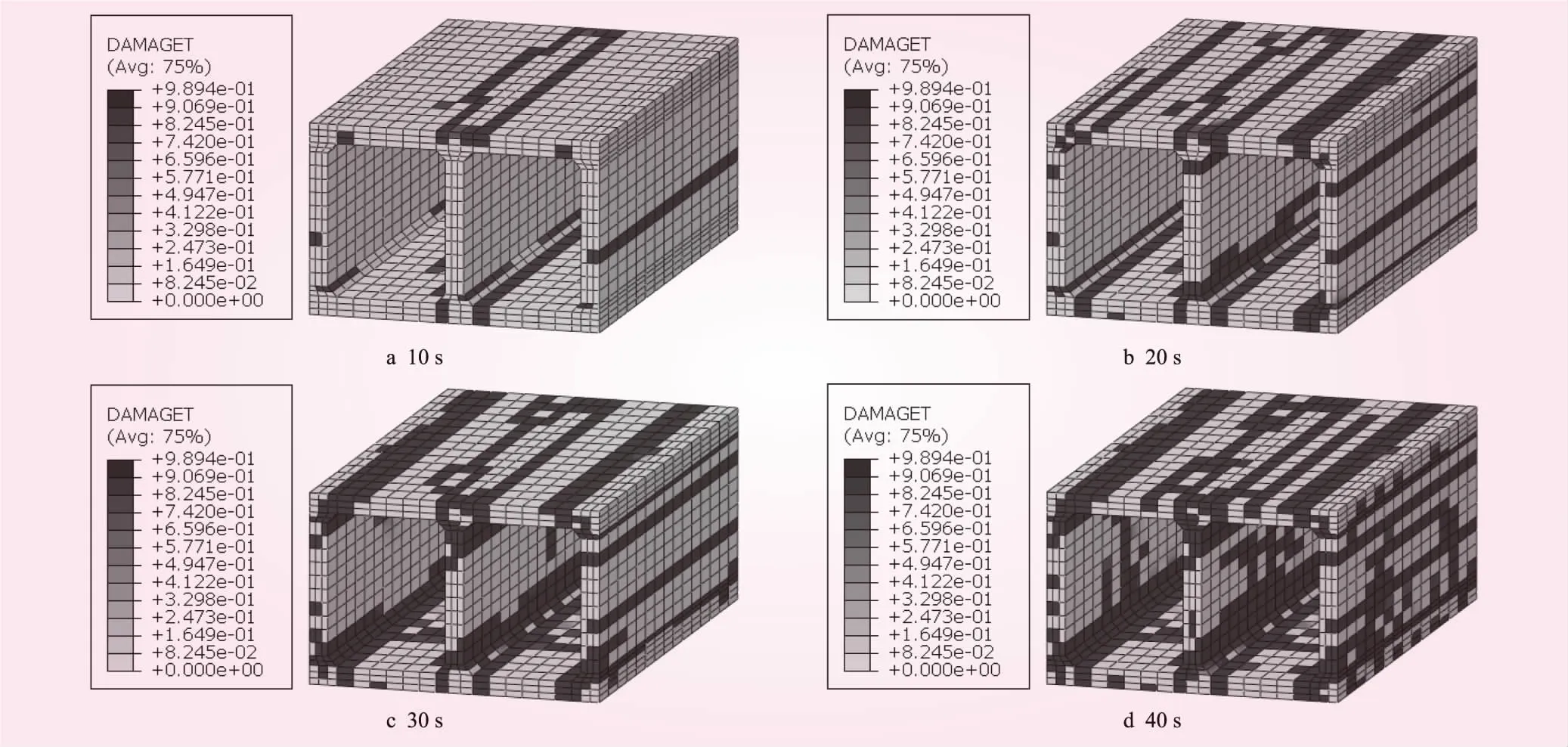
图12 有内水压工况下不同持时箱涵受拉损伤分布

图13 无内水压工况下不同持时箱涵受拉损伤分布

(1)在ETA曲线峰值加速度为0.15g的前10 s中，2种工况下箱涵主要在顶板和底板靠近中墙位置首先发生损伤破坏。而在有内水压力的情况下，箱涵侧墙外部有可能发生横向表面裂缝。

(2)当耐震时程达到20 s时，此时峰值加速度约为0.3g。有内水压力工况下，箱涵中墙的上部和下部连接处发生贯穿性损伤，顶板和底板靠近侧竖墙位置发生部分贯穿性损伤，并在箱涵的外表面产生多条横向的表面损伤裂缝；相比在无内水压力工况下，在原有损伤基础上，新的损伤多发生在箱涵的顶板和底板的内表面。

(3)当耐震时程达到30 s时，此时峰值加速度约为0.45g。在2种工况下，箱涵的损伤区域在此前的基础上，在顶板和底板与竖墙的连接处进一步延伸。而在有内水压力时，箱涵内部中墙出现沿竖向发展的损伤，顶板与底板出现多处横向贯穿性损伤，此时箱涵结构的损伤程度可能会对其正常稳定运行产生较大影响。

(4)当耐震时程达到40 s时，此时峰值加速度达到最高约为0.6g。在有内水压力工况下，箱涵损伤区域几乎贯穿遍布整个箱涵的内外表面，中墙损伤破坏最为严重，箱涵整体处于严重损伤状态，可以判定箱涵几乎失去正常运行的能力；在无内水压力工况下，箱涵的损伤区域多在内表面扩展，贯穿性损伤也只出现在顶板和底板的边缘位置以及竖墙的上下连接处，相对有内水工况下损伤程度要小。

4 结 语

本文运用耐震时程法对浅埋压力箱涵进行抗震分析，通过对压力箱涵有内水压力状态和无内水压力状态2种工况进行动力计算，考虑了结构与土体间的相互作用，分析压力箱涵在不同地震强度下的下动力响应情况，得到以下结论：

(1)耐震时程法能够直观反映出压力箱涵在不同强度下的动力响应情况，具有较高的计算分析效率。在2种工况下，浅埋压力箱涵在地震动作用下侧向相比竖向更易发生较大位移，且两种工况下各持时的最大累计位移相差不大。

(2)在有内水压力工况下，从第10 s起，压力箱涵顶板相对底板的竖向残余变形开始呈现随时间增长而逐渐向外快速增大的趋势，而外侧墙相对中墙的侧向残余变形在整个计算周期也逐渐向外增大；相比无内水压力工况下，在峰值加速度较小时，竖向残余变形以及侧向残余变形呈现向箱涵内部变化的趋势，随着峰值加速度的增大，逐渐转变为向外增大趋势。

(3)通过分析压力箱涵相同持时下损伤分布情况，有内水压力工况相比无内水压力工况损伤更为严重，且有内水压力时箱涵损伤大多从外表面开始扩展，而无内水压力时箱涵损伤大多从内表面开始扩展。在有内水压力工况下，当ETA曲线峰值加速度达到0.45g时，箱涵结构转折处损伤较为严重，对其正常运行可能产生严重影响，或达到其极限抗震能力；在无内水压力工况下，箱涵的抗震能力更强。