融合光流与MARG 传感器的三维姿态测量研究*

石 琦，李 翔

(桂林电子科技大学电子工程与自动化学院，广西 桂林 541004)

光流传感器是一种能从连续图像流中获取运动信息的传感器，近年来被广泛用于无人机中，与加速度计、陀螺仪、磁强计(合称MARG 传感器，即磁强计magnetometer、加速度计accelerometer 及速率陀螺rate gyro 的缩写[1]，亦可解释为磁magnetic、角速度angular rate 和重力gravity 三种测量对象的缩写[2-4])等传感器相结合，以实现无人机的飞行控制。光流传感器用于无人机飞控的一种典型方案是采用竖直向下安装的单个光流传感器，通过其测量值获取无人机相对于地面的水平运动，可提高无人机定点悬停的位置精度[5-6]。但在此种方案中，光流传感器的测量值实际上是无人机的平移、俯仰和横滚三种运动共同作用的结果。因此，要想从光流测量值准确获取无人机的平移运动，需要借助惯导(Inertial Navigation System，INS)提供的姿态信息或者陀螺仪提供的角速度测量值，将无人机姿态变化引起的光流加以消除，才能得到准确的水平速度(或位移)[7-11]。

如上所述，光流传感器的测量值可分为平移分量与转动分量两部分，分别与载体的平移运动和旋转运动相关。然而上述将光流传感器用于无人机的方案中，只用到了平移运动形成的光流(平动光流)，而对于载体转动造成的光流(转动光流)则借助IMU 陀螺仪提供的角速度将其消去。此类用法的缺点在于:一是未能充分利用转动光流包含的姿态信息；二是在消去转动光流时易将惯导或陀螺仪的误差代入到平移速度(或位移)的计算中。

在航天器控制领域，利用转动光流获取载体姿态信息的方法较为多见，如文献[12]采用扩展卡尔曼滤波器(Extended Kalman Filter，EKF)由光流估计三轴角速度，文献[13]和[14]采用多种不同的卡尔曼滤波算法由光流估计航天器的三轴角速度，文献[15]对星空成像进行预处理后再提取光流数据以计算角速度。此类方法的问题是成像范围内星体数目较多时，获取光流所需计算量较大，且涉及非线性测量模型，需采用非线性的卡尔曼滤波算法(如EKF)。在无人机领域，文献[16]尝试采用光流传感器测量无人机三维姿态，然而其所用算法也采用非线性测量模型，同样存在求解复杂、计算量大等问题。

为充分利用光流传感器测量值中包含的姿态信息，提出一种简单的线性测量模型，可从光流测量值中提取角速度，并进而将获得的角速度与陀螺仪测量值根据最小方差准则进行融合以减小角速度测量误差，最后将融合后的角速度与加速度计及磁强计数据利用EKF 算法进行融合，以提高三维姿态的估计精度。通过实验验证了所提出的测量模型和算法的有效性。

1 光流传感器测量模型

光流传感器工作原理如图1 所示，由于通常情况下物距d远大于焦距f，故可认为像距近似等于f。由图1 可见，凡是垂直于传感器主光轴的运动均可产生光流，而旋转运动与平移运动均可切割主光轴，故旋转与平移均可产生相应的光流。因此，可将光流传感器的测量值视为平移光流与转动光流的叠加。

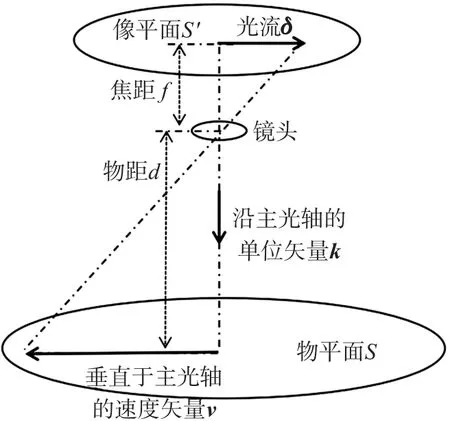
图1 光流测量原理

首先考虑传感器载体仅有平移运动的情况。设垂直于主光轴的平移速度为v，由平移造成的光流为δv，则由图1 所示几何关系可知δv正比于v，如式(1)所示，其中k为沿主光轴的单位矢量。可见平移光流δv与物距d成反比。

其次考虑传感器载体转动形成的光流。设载体角速度为ω，由其造成的光流为δω，经分析可知二者关系如式(2)所示。可见转动光流δω与物距d无关。

光流传感器的测量值应是上述两部分光流的叠加，即

2 基于光流的角速度测量

由式(3)可知，当传感器载体只进行旋转运动时，光流测量值仅与角速度有关。光流与角速度的关系式即式(2)可改写为矩阵形式，如式(4)所示。由于角速度ω为三维矢量，而转动光流δω是像平面内的二维矢量，故式(4)中的Uω是一个2×3 常系数矩阵，它反映了光流传感器在b系中的安装方向。

将式(4)推广到采用多个不共面光流传感器进行测量的情形，则得到式(5):

式中:δωk表示第k个光流传感器的测量值(其中k＝1，2，…，N)，Uωk为第k个光流传感器对应的常系数矩阵。注意每个光流传感器的测量值(即δωk)都是二维矢量(包含像平面内两个正交方向的光流测量数据)，故Vω为2N×3 的常系数矩阵，由各光流传感器在b系中的安装角度确定。式(5)可视为关于角速度的超定方程组，可利用最小二乘法进行求解，如式(6)所示:

式中:ωof表示由光流测量值解算出的角速度。实际应用中，式(6)还可以进一步简写为式(7)，其中W＝是一个3×2N的常系数矩阵，只要能获知角速度的真值，即可直接由光流测量值和相应的角速度真值求出W。

3 光流与MARG 传感器的融合

3.1 算法整体流程

如上所述，光流传感器可用于测量三维角速度，将其与MARG 传感器进行数据融合有助于改善姿态估计精度。为此，设计了如下的数据融合与姿态估计流程:

①从光流传感器测量数据中提取三维角速度；

②将光流传感器获取的角速度与陀螺仪测量得到的角速度进行融合；

③将融合后的角速度数据与加速度计及磁强计测量值一同代入EKF 估计姿态。

算法整体流程框图如图2 所示，其中:ωof表示由光流测量值提取的角速度，ωg为陀螺仪测得的角速度，ωs为二者融合后的角速度，g为加速度计测得的重力矢量，h为磁强计测得的地磁矢量。

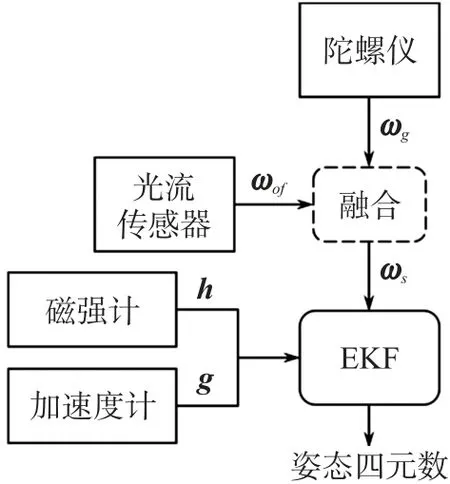
图2 数据融合及姿态估计算法流程框图

3.2 基于最小方差准则的角速度融合

光流传感器和陀螺仪均能测量载体的三维角速度，将两者的测量值进行加权可提高测量精度，具体做法是按最小方差准则进行融合，如式(8)所示:

3.3 基于EKF 的姿态估计

选取姿态四元数q＝(q1q2q3q4)T作为状态向量(q1为标量部分，其余三个分量为矢量部分)，利用EKF 进行姿态估计，递推流程如下。

EKF 算法第一步(状态预测):

式中:表示(k-1)时刻的验后估计，表示k时刻的状态预测值即验前估计，Φk/k-1表示从(k-1)时刻到k时刻的状态转移矩阵，如式(10)所示，ωsx，k、ωsy，k和ωsz，k分别表示k时刻ωs的三轴分量，T为采样周期。

式中:Pk-1/k-1为(k-1)时刻的验后方差，Pk/k-1为k时刻的验前方差，Qk为过程噪声协方差阵。Qk由式(12)计算，其中Rω为角速度的协方差阵，Sk是由k时刻的姿态四元数按式(13)构造的雅可比矩阵，q1～q4依次为k时刻姿态四元数的四个分量。

EKF 算法第三步(状态修正):

由k时刻的加速度计测量值gk与磁强计测量值hk构成EKF 的观测量Zk，如式(14)所示:

式中:量测矩阵Hk可由式(16)求得。由于和分别为4 维和6 维向量，故Hk为6×4 矩阵。式(16)中:g0为本地重力加速度，hN及hU分别为地磁场的北向和天向分量。

接下来由式(17)求出k时刻的卡尔曼增益Kk，其中Rk为量测噪声协方差阵，由磁强计的噪声协方差阵Rh及加速度计的协方差阵Rg根据式(18)构造而成。

由卡尔曼增益可得k时刻的验后估计(状态修正)如式(19)所示:

4 实验验证

4.1 实验条件

实验采用的光流模块型号为LC302，将三个光流模块布置于两两正交的三个平面上，如图3 所示。此外，实验中还采用型号为IMU901 的MARG 传感器模块与图3 所示光流模块进行数据融合与姿态解算。

图3 实验所用光流传感器模块

采用型号为WTGAHRS1 的惯导模块提供三维姿态基准，其姿态角精度可达静态0.05°、动态0.1°，可作为三维姿态的真值，实验中将其与光流模块及航姿模块互相固定，使得三者能够同步转动。数据采集时，手持模块进行无规则转动，使用串口接收数据进行统一处理，并将数据导入MATLAB 中进行解算。由WTGAHRS1 模块测得的三维姿态变化如图4 所示。

图4 三维姿态角变化曲线

4.2 角速度测量及融合结果

以惯导模块WTGAHRS1 提供的三维角速度数据作为真值，首先求出式(7)中的常系数矩阵W，如式(21)所示:

得到矩阵W后，再将其代入式(7)，即可从光流传感器测量值解算出角速度ωof。

接下来按式(8)将ωof与陀螺仪测量的角速度ωg进行融合得到ωs。由实测数据分别计算ωof和ωg的均方根误差(Root Mean Square Error，RMSE)，结果如表1 所示。将各轴角速度的RMSE 取平均后代入式(8)即可得到加权系数，从而由ωof和ωg加权后得到ωs，其RMSE 亦列于表1 中。由表1 可见，式(7)所给出的线性测量模型能够有效地从多个不共面安装的光流传感器测量值中提取三维角速度信息，且测量精度与低成本MEMS 陀螺仪相当。将光流传感器获取的角速度信息与陀螺仪测量值进行融合后，可进一步提高精度，使三轴角速度的误差限制在1°/s 以内。

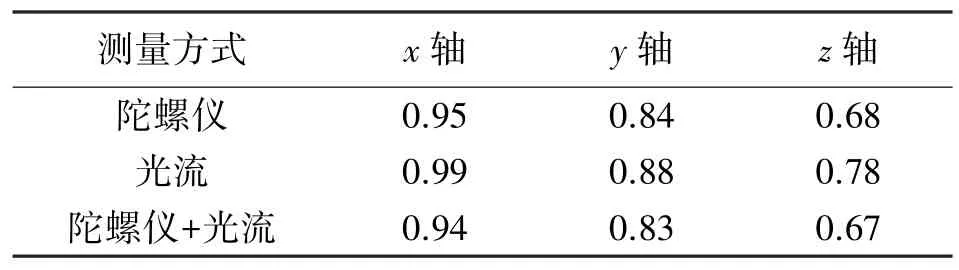
表1 三维角速度误差(RMSE) 单位:(°)/s

4.3 EKF 姿态估计结果

采用3.3 小节中的EKF 算法进行三维姿态估计，各传感器的噪声协方差阵取值为:Rω＝2.5×10-4I3×3，Rh＝4×10-4I3×3，Rg＝10-6I3×3，其中角速度的噪声协方差参考表1 所列RMSE，重力及地磁矢量的噪声协方差则由加速度计和磁强计噪声分别经过矢量单位化处理后得到。此外，对重力及地磁矢量均作单位化处理后，式(16)所示量测矩阵Hk中的g0相当于变为1，而hN及hU则直接由本地的地磁倾角γ确定，实验中测得γ≈39°，即hN≈cos39°，hU≈-sin39°。

在EKF 算法中分别采用两种不同来源的角速度数据:陀螺仪测量值ωg及其与光流传感器融合后的角速度ωs。将EKF 输出的姿态四元数转化为欧拉角，与惯导模块WTGAHRS1 提供的姿态角真值进行比较，结果如表2 所示。可见，引入光流解算的角速度后，有助于提高姿态测量的精度。

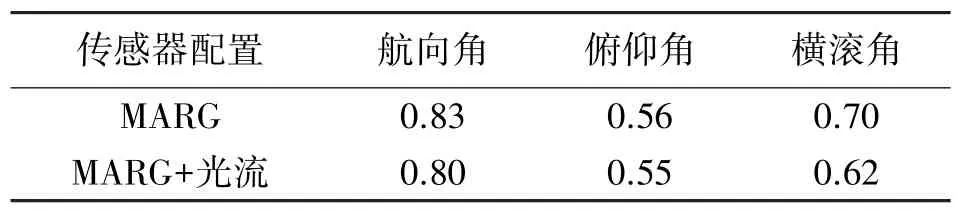
表2 三维姿态角误差(RMSE) 单位:(°)

5 结束语

提出一种利用光流传感器解算角速度并与陀螺仪进行融合的方法，采用线性测量模型由光流测量值解算出三维角速度，并将其与MARG 传感器中的陀螺仪按最小方差准则进行融合，再以融合后的角速度构建EKF 的状态方程，以加速度计与磁强计数据构建EKF 量测方程。实验结果表明，所提出的方法改善了基于MARG 传感器的姿态估计精度，提供了一种姿态测量的新途径，有助于提升姿态测量系统的冗余度。