基于动态逆控制的高超声速飞行器飞/发一体化控制方法研究

闫斌斌, 林泽淮, 刘双喜, 闫杰

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.国防科技大学 空天科学学院, 湖南 长沙 410073;3.国防科技大学 高超声速技术实验室, 湖南 长沙 410073; 4.西北工业大学 无人系统技术研究院, 陕西 西安 710072)

高超声速飞行器是指飞行速度大于5Ma的新型飞行器,具有飞行速度快、突防能力强、作战空域广、反应时间短等特点[1-3]。目前,高超声速飞行技术已经成功应用到各国巡航导弹、空天飞机、可重复使用运载器、无人机等各种类型飞行器的研制中[4]。尽管高超声速飞行器具有广阔的应用前景,但其作为一种高度复杂的飞行器,高超声速飞行器和发动机之间呈现出极强的耦合性特点,这给飞行/推进系统控制带来了困难与挑战:传统的飞行器和发动机设计是通过协调确定物理界面以及机械、电气和通信接口后独立进行的,不考虑相互间的耦合作用,使得飞机和发动机均难以发挥最大的性能潜力。

飞/发一体化控制(integrated flight-propulsion control,IFPC)技术是综合考虑和充分利用对飞行器和发动机的控制作用及其相互影响,使飞行器可以最大限度地发挥其性能潜力,以满足新任务能力的需求[5]。由于高超声速飞行器与发动机一体化的设计方式,导致空气动力学、结构动力学与推进系统之间存在显著的交叉耦合效应,这在客观上要求对高超声速飞行器和发动机进行一体化控制。采用飞/发一体化控制可以提高系统的整体性能,实现飞行器和发动机的最优匹配,极大地增强高超声速飞行器的作战能力[6]。

非线性动态逆(nonlinear dynamic inversion control,NDI)广泛应用于飞行器非线性控制中[7-8]。文献[9]针对舰载机人工着舰精确轨迹控制中飞行员操纵负担重、着舰环境复杂的问题,采用NDI控制方法设计了舰载机着舰轨迹控制律。针对具有输入饱和的非仿射纯反馈非线性系统,文献[10]基于奇异值摄动理论设计了NDI控制器,该控制器不仅具有较好的跟踪性能与有效性,还避免了反步法中的复杂性爆炸问题。文献[11]针对吸气式高超声速飞行器巡航状态下飞行环境复杂、建模时存在非线性以及参数摄动等问题,提出了一种非线性动态逆-滑模控制律改进方法,在NDI的基础上采用滑模变结构补偿参数摄动带来的误差。针对纵列式直升机存在的强耦合、强非线性、旋翼之间气动干扰大及非线性模型难以求解问题,文献[12]设计了基于BP神经网络的动态逆控制器,有效降低了系统超调量、减小系统响应时间。针对旋转导弹旋转带来的横向与纵向之间的交叉耦合效应,文献[13]利用NDI方法进行解耦控制,并加入了非线性干扰观测器,保证了系统的鲁棒性。实际上,NDI控制方法高度依赖于所建模型的准确性,在工程实践中难以达到最理想的控制效果,而增量非线性动态逆(incremental nonlinear dynamic inversion control,INDI)控制方法在保证控制性能的基础上降低了对模型精确度的要求,应用更加广泛[14]。

本文以X-43A高超声速飞行器为研究对象,开展飞/发一体化控制方法与控制策略研究。根据飞/发耦合特性和耦合模型,基于多输入-多输出(MIMO)设计理论和NDI、INDI控制方法,分别设计了姿态外回路NDI控制器与角速率内回路INDI控制器,以及高度和速度PID控制器,并通过设计操纵交联的形式对发动机进行耦合补偿,从而形成了飞/发一体化控制策略,保证了高超声速飞行器的飞行品质和控制器的鲁棒性。

1 高超声速飞行器模型

针对飞/发一体化的控制问题,建立高超声速飞行器的六自由度非线性运动模型。

高超声速飞行器位置动力学方程为

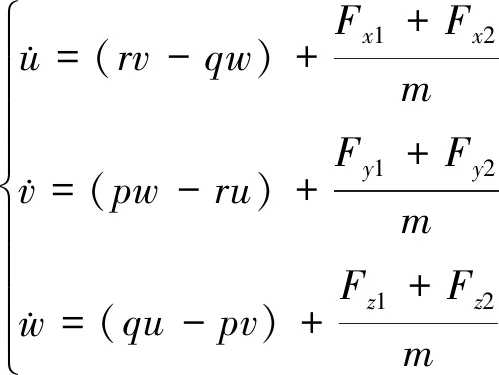
(1)

式中:u,v,w表示机体坐标系下的速度分量;p,q,r分别表示滚转角速度、俯仰角速度和偏航角速度;m表示高超声速飞行器质量;Fx1,Fy1,Fz1和Fx2,Fy2,Fz2分别表示高超声速飞行器所受气动力和发动机推力在机体坐标系下的分量。

高超声速飞行器位置运动学方程为

(2)

式中,Ldf和Lbd分别表示北东天坐标系至地心地固坐标系的转换矩阵,以及机体坐标系至东北天坐标系的转换矩阵

式中:λ与φ分别表示NED坐标系原点所处的地理经度和纬度;φ,θ,ψ分别表示高超声速飞行器的滚转角、俯仰角和偏航角。

高超声速飞行器姿态动力学方程为

(5)

式中:Ixx,Iyy,Izz表示转动惯量;Mx,My,Mz分别表示滚转力矩、俯仰力矩和偏航力矩。

高超声速飞行器姿态运动学方程为

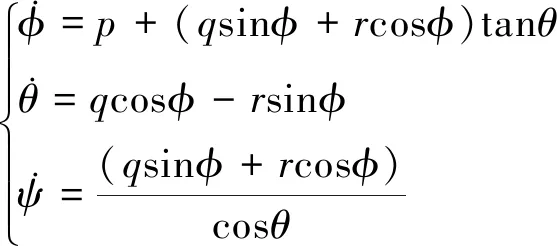
(6)

补充方程

(7)

式中,α和β分别表示高超声速飞行器的迎角和侧滑角。

本文中舵面和发动机油门等执行机构回路由二阶模型表示

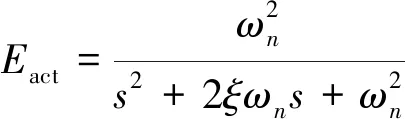
(8)

式中:ξ=0.7;ωn=25 Hz。

2 基于非线性动态逆的控制器设计

2.1 NDI理论

考虑非线性系统状态方程为

(9)

则控制系统输出方程可表示为

(10)

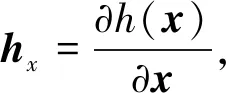
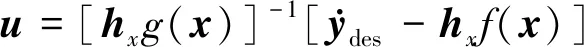
(11)

显然,构造的NDI控制律包含控制系统状态参量的反馈项f(x),所以控制效果高度依赖被控对象数学模型的精确程度。

2.2 INDI理论

为提高NDI控制的鲁棒性,有关学者提出了INDI控制方法,通过计算增量指令来代替总的控制输入,降低控制律对于被控对象模型的依赖性[15]。

将(9)式中的系统状态量x在[x0,u0]的小邻域内泰勒展开,可得

(12)

定义

(13)

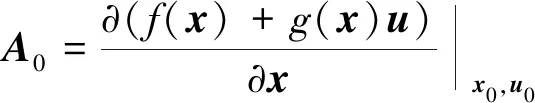
(14)

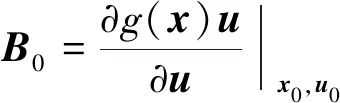
(15)

Δx=x-x0

(16)

Δu=u-u0

(17)

那么(12)式可改写为

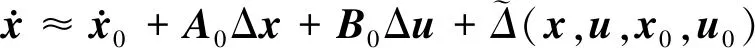
(18)

忽略高阶项,则(18)式可线性近似表示为

(19)

当控制律的解算频率足够高时,状态量的增量Δx相对于控制输入的增量Δu是高阶小量,因此A0Δx可以忽略,则

(20)

控制系统输出方程可写为

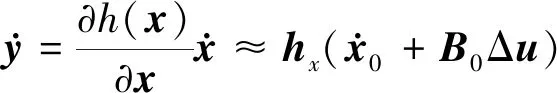
(21)

(22)

最后可得到增量INDI控制器的输出为

u=u0+Δu

(23)

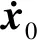
2.3 控制器设计

本文根据奇异摄动理论,采用姿态角速率内环与姿态外环分离的控制方案。其中,姿态外环控制系统输入为姿态角误差,输出控制量为姿态角速率期望值。由于姿态外环系统中无摄动较大的参数,且控制系统易由状态方程准确表示,不存在模型的不确定性,为降低姿态外环控制律解算频率与复杂度,姿态外环选用NDI控制。角速率内环控制系统存在气动系数等摄动较大的参数,且精确模型建立较复杂,为保证控制系统鲁棒性,角速率内环选用INDI控制。同时,通过升降舵偏角与发动机油门操纵交联的形式进行发动机对高超声速飞行器的耦合补偿。

为实现速度控制无静差以及高度控制的平滑稳定,本文对于速度与高度回路分别选用PI控制与串级PID控制律。控制器的总体结构如图1所示。

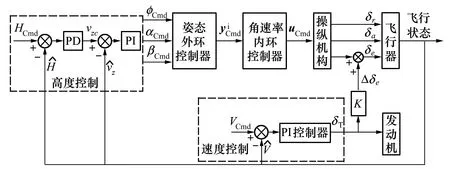
图1 飞/发耦合控制结构

其中,K表示发动机对俯仰通道的操纵交联。为使俯仰舵偏角增量能够抵消发动机对俯仰通道的影响,即满足

(24)

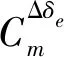
操纵交联可表示为

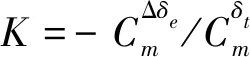
(25)

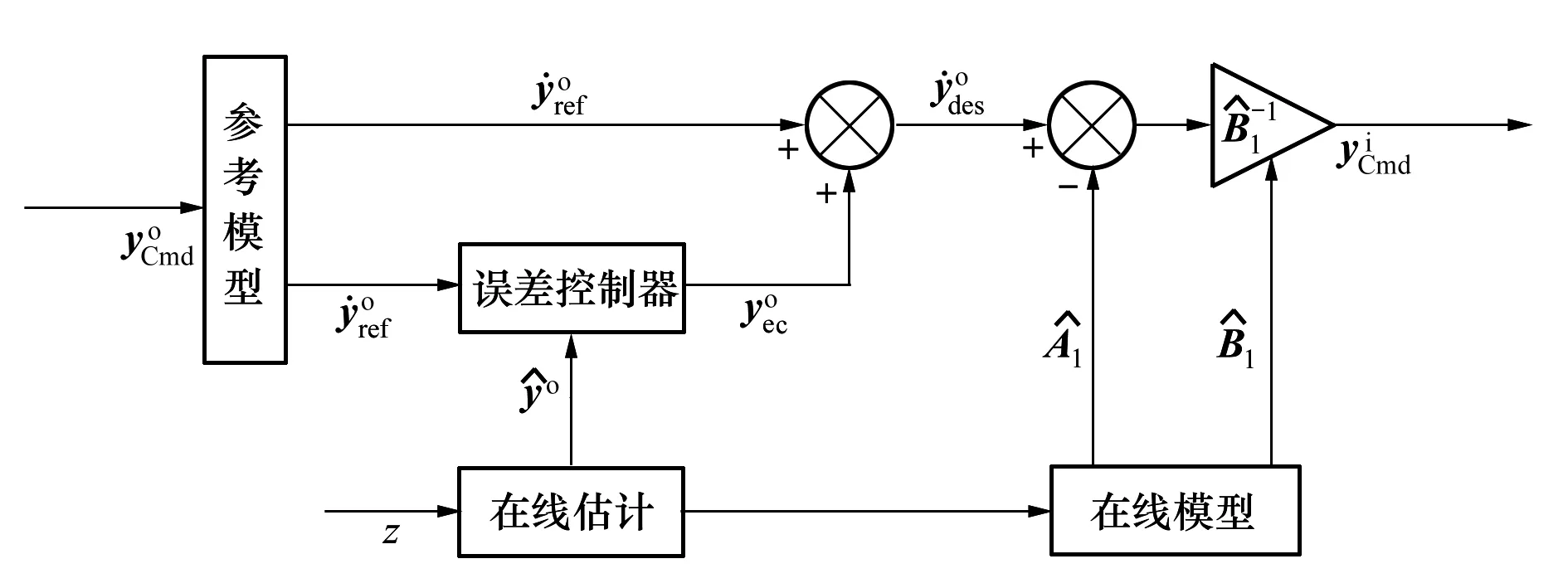
图2 姿态外环NDI控制器结构

图3 角速率内环INDI控制器结构

下面对姿态控制器的子模块进行详细设计:

1) 参考模型

参考模型结构如图4所示,其中τ为时间常数。

图4 参考模型

2) 误差控制器

外环误差控制律可表示为

(26)

内环误差控制律可写为

(27)

其中,控制增益可根据系统可控能力、时间尺度分离原则和执行机构/操纵机构动力学特性进行优化设计。

3) 指令转换

将角加速度作为角速率内环直接被控状态量时,根据INDI控制原理,需实时获取当前角加速度,为避免直接测量角加速度时存在噪声及延迟的问题,本文选择力矩作为角速率内环直接被控状态量,因此需将角加速度期望值转换为力矩期望值。指令转换模块通过欧拉方程可得出力矩期望值Mdes

(28)

式中,I表示机体转动惯量矩阵。

4) 在线模型

在计算外、内环控制量输出时,根据模型与控制律的不同,需要在线计算不同的矩阵。

对于姿态外环,其控制系统状态方程为

(29)

根据NDI控制原理,姿态外环控制输出为

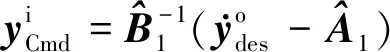
(30)

(31)

(32)

对于角速率内环,其控制系统状态方程为

M=A2+B2uCmd

(33)

根据INDI控制原理,A2矩阵不需要建模及在线求解,姿态外环控制输出为

(34)

式中,u0为上一时刻的舵偏量,由在线估计模块得出。

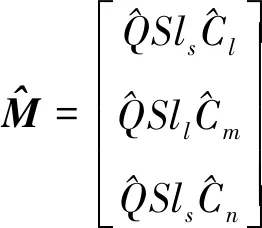
(35)

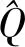
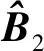
(36)

3 仿真分析

根据建立的具有耦合特性的飞/发一体化模型,以及所设计的飞/发一体化控制策略,对基于NDI、INDI的高超声速飞行控制器的有效性进行仿真飞行验证。仿真初始条件如如表1所示。β,φ,q,p,r,δr,δa为0。

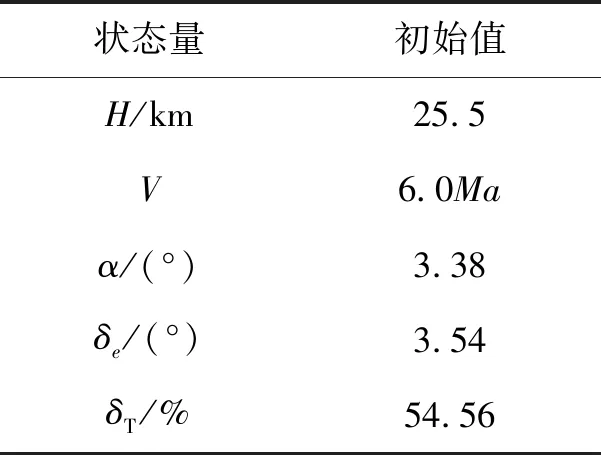
表1 仿真初始条件

3.1 纵向通道仿真

在本小节中,假设高超声速飞行器以6Ma速度在25.5 km高度飞行,高度回路设置斜方坡指令,侧滑角指令为βc=0°,滚转角指令为φc=0°,仿真结果如图5所示。其中,黑色虚线为控制器指令(Cmd)曲线,蓝色虚线为经典PID控制仿真曲线,红色实线为INDI控制仿真曲线。

图5 纵向通道仿真结果

由图5可知,在飞行高度方面,当高超声速飞行器高度指令为稳定保持25.5 km平飞时,INDI控制的跟踪效果优于经典PID控制,且INDI控制高度误差峰值较经典PID控制更小;在飞行速度方面,INDI控制较经典PID控制速度误差峰值更小,速度跟踪响应的稳态与快速性也更好;在高超声速飞行器姿态方面,迎角变化曲线与发动机油门量的变化曲线趋势接近,表明纵向的动态响应过程引起了速度通道的扰动变化。此外,在高超声速飞行器纵向运动过程中,侧滑角、滚转角变化很轻微,表明在高超声速飞行下,飞行器的纵向运动没有引起明显的横航向扰动响应。

综上所述,INDI控制方法可较好地实现高超声速飞行器纵向通道间与发动机的耦合控制。纵向控制及解耦效果方面,INDI控制策略在解耦效果、快速性、稳态误差性能方面,都优于经典PID控制,且在同等性能条件下,INDI控制策略避免了复杂的增益调度设计过程。

3.2 横向通道仿真

在本小节中,假设高超声速飞行器以6Ma速度在25.5 km高度飞行,侧滑角指令为βc=0°,滚转回路设置为斜方坡指令,仿真结果如图6所示。

图6中黑色虚线为控制器指令(Cmd)曲线,蓝色虚线为经典PID控制仿真曲线,红色实线为INDI控制仿真曲线。由图6可知,在滚转角指令跟踪方面,INDI控制无明显超调量,跟踪精度优于经典PID控制;在飞行高度与速度方面,INDI控制的高度误差与速度误差均小于经典PID控制;在高超声速飞行器姿态方面,迎角变化趋势与油门杆增量变化趋势相同。为实现精确耦合控制,INDI控制的横航向用舵量比经典PID控制大。

综上所述,相较于经典PID控制,INDI控制方法对高超声速飞行器横向强耦合作用控制性能更佳。

4 结 论

针对高超声速飞行器飞行过程中的飞/发间耦合效应对自身的影响,本文在建立的高超声速飞行器飞/发一体化数学模型基础上,基于奇异摄动理论,将控制系统分解为角速率内回路和姿态外回路,对外、内回路采用NDI、INDI方法分别进行控制回路设计;然后,为增强控制系统的鲁棒性,在控制器中引入了在线估计、误差控制器、在线模型、参考模型等模块;最后,通过仿真验证了控制算法能有效实现飞/发耦合控制,降低耦合效应对高超声速飞行器自身的影响,且相比经典PID控制,本文所设计的控制方法具有更快的响应速度与更高好的控制精度。