基于模型聚类的说话人识别研究∗

陈秉沃 张二华 唐振民

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

传统说话人识别技术是通过采集说话人语音数据，然后从语音数据中提取特征参数，并代入到训练好的高斯混合模型中进行逐一打分，得分最高的即是所匹配的说话人。随着说话人识别技术的广泛应用，说话人模型数量不断增长，若依然采用传统的说话人识别方法，就会造成两个问题。其一是说话人识别的耗时过长，效率低下；其二是说话人识别的准确性大大降低。为了解决这两个问题，本文对不同距离定义的聚类效果进行对比，选取一种最佳的聚类方法，将其应用于说话人识别中。使得识别效率大大提高，识别准确率也有所提高。

2 大规模条件下的说话人识别

2.1 传统说话人识别存在的问题

传统的说话人识别技术分为两个部分。第一部分是利用所有说话人的训练语音建立各人的高斯混合模型，作为后端模型数据库。第二部分是前端处理，采集说话人的语音，进而提取特征参数，再将数据逐一代入后端说话人模型中，取得最高分模型，如果此模型对应的说话人与前端所采集的说话人为同一人，则表明识别准确。

大规模条件下的说话人识别，采用传统的逐一匹配方式会使单人识别耗时随后端说话人数量成正比增长，即当说话人规模扩大时，单人识别耗时也会随之大幅提升，这严重影响系统的实用性。另外，随着说话人规模的不断扩大，说话人识别准确率也随之降低。

本文的传统说话人识别中，使用N 阶高斯混合模型，其中N 为32，训练语音为10s，测试语音为10s。在不同规模下的说话人识别的平均单人识别耗时，以及识别的准确率，如表1所示。

表1 不同说话人规模的识别耗时以及总体识别准确率

由表1 可见，当说话人规模（Speaker Count，SPKC）为数百人的时候，单人识别时长仅需数秒，总体识别耗时为数百秒，说话人识别的准确率也尚可。但是当说话人规模达到近千级别时，单人识别耗时已经达到了十几秒，总体识别耗时达到上万秒，识别准确率也明显降低，这严重影响了说话人识别系统的实用性。一个好的说话人识别系统，不仅要考虑高效性，而且需要考虑准确性。在大规模说话人的背景下，显然使用传统的说话人识别系统无法满足系统的实用性要求。因此本文考虑采用模型聚类的方法，对传统识别方法进行改进。

2.2 说话人识别聚类算法

简单来说，聚类思想就是把一些相似的对象归为到同一簇中。簇内的对象越相似，并且不同簇之间的距离越远，那么聚类的效果就越好。在说话人识别中也是如此，将聚类思想应用于说话人识别就是进行两步判别，第一步，先判别待识别的说话人对象最接近哪一类的类中心，其中，类中心指的是某一类的代表。第二步，对类中所包含的说话人模型再使用传统方法进行逐一判别。由此可见，聚类的效果以及聚类的数目直接影响到说话人识别系统的总体性能。

由于聚类算法的局限，聚类结果中每一类的规模可能大小不一，因此，在识别中的第二步所对应的最近一类的说话人规模大小也呈现不确定性。因此，引入搜索率的概念。搜索率，指的就是此次识别搜索的说话人规模Q1与总体说话人规模Q 的比例，那么搜索率Z如式（1）所示。

每次搜索，都由距离由近及远进行搜索，先从距离模型最近的类开始搜索，直到搜索的说话人规模占比达到预先给定的搜索率。从林文勇［3］的论文可知，在说话人模型匹配中，有十分之一的模型得分比较高，说明每次匹配具有十分之一的模型比较相似，因此，本文设置搜索率为10%。在基于聚类的说话人识别中，聚类效果的好坏使用命中率来衡量。一次命中指的是，在一次搜索中，所搜索的说话人模型中，正好包含着与测试说话人相对应的说话人模型。命中率（Accuracy Rate，AR）则是说话人测试集合中，命中个数的占比。命中率越高，说明聚类的效果就越好。命中率公式如式（2）所示。

其中，AR为命中率，AC为说话人测试集中命中的个数（Accuracy Count，AC），SPKC 为说话人规模（Speaker Count，SPKC）的缩写。

基于模型聚类的说话人识别的第二步识别步骤和传统说话人识别方式一样，都是进行传统的逐一匹配，但经过聚类后所需匹配的说话人模型规模大为减少。由此可见，第一步聚类效果的好坏直接影响到最后识别的效果。在聚类过程中，常用并且高效的算法为k-means 算法，可以适用于大规模条件下的说话人识别系统。因此，本文采用k-means算法作为说话人模型聚类的算法，总体流程如下：

1）初始化类，确定聚类数目，并随机选取k 类作为初始类。

2）求剩余的说话人与每一类的类中心的距离，并并入最近的一类。

3）更新每一类的类中心Ci，并令D 等于目前的说话人数量。

4）而后随机抽取任意一类的任意样本，即某一说话人模型，求得模型离本类中心的距离以及和其他类的类中心的距离。如果离本类的类中心距离是最近的，则让D 自减1，当自减至0 时退出循环。如果不是则将此说话人归入最近的一类中，然后跳到3）重新循环3）～4）步骤。

2.3 聚类距离选取的研究

2.3.1 基于KL散度的聚类方法

相对熵又称为交叉熵，Kullback-Leible 散度（即KL 散度）等。设p（x）和q（x）是两个概率分布，则p对q的K-L散度如式（3）所示。

KL 散度是两个概率分布P 和Q 差别的非对称性的度量，在一定程度上可以来衡量两个分布之间的距离。但是，尽管KL 散度从直观上是个度量或距离函数，但它实际上并不是一个真正的距离尺度，因为它并不具备对称性，如式（4）所示。

因此在聚类中，将KL 散度运用到高斯混合模型的KL距离时，可以采用加权公式来计算，如此两个模型之间的距离便变为固定值，如式（5）所示。

目前已经有两个多元高斯混合模型的KL散度数学解析形式。如式（6）所示。

其中，Sm和um分别是第m个说话人的一阶高斯混合模型的协方差和均值向量。但是，说话人识别所用的是N 阶高斯混合模型S={ai,μi,Σi}，如式（7）所示。

表2 基于KL散度的模型聚类方法

由表2 可以看出，命中率并不理想，原因是KL散度并不具备对称性，即使采用了加权的算法，也依然不是一个很好的距离定义。并且随着聚类数目增多，命中率逐渐降低。原因是使用一个并不精准的距离定义进行聚类，随着聚类数目越多，聚类效果就越差，因此命中率会随着聚类数目的增多而下降。因此KL散度并不适用于作为模型聚类的距离定义。

2.3.2 基于替代模型Wasserstein distance 的聚类方法

因为KL散度不具备对称性，所以KL散度并不适用于计算两个分布之间的距离。通常，可以使用具有对称性的Wasserstein 距离来计算两个分布之间的代价距离。Wasserstein 距离也叫做推土机距离（Earth Mover's distance），这是因为该距离定义中由一个分布转变为另一个分布所需要的代价和挖土填土的过程十分相似。目前已经有两个一阶多元高斯混合模型之间的Wasserstein 距离的数学解析形式［16］，如式（8）所示。

其中Sm和um分别是第m 个说话人的一阶高斯混合模型的协方差和均值向量，F是Frobenius范式。

得到第m 个说话人模型S={ai,ui,Σi}的替代模型后，就可以直接使用Wasserstein distance 在多元高斯混合模型的解析公式进行计算，解析公式见式（8）。并且在聚类过程中，某一个类的类中心同样采用加权的算法，假设第k 类的说话人个数为Lk，那么第k 类的类中心Ck=｛uk，Sk｝的加权平均向量uk和加权协方差Sk计算公式则如式（11）以及式（12）所示。

得到第k 类的类中心的参数后，用该参数对应的一阶多元高模型来作为该类的类中心模型，可以得到说话人替代模型与第k 类的类中心的替代模型Ck=｛uk，Sk｝之间的距离d2(,Ck)，如式（13）所示。

采用423 人份1min 训练时长的电话语音对N阶高斯混合模型进行训练，测试时长也为1min，搜索率设置为10%，基于近似模型Wasserstein distance的聚类方法的命中率如表3所示。

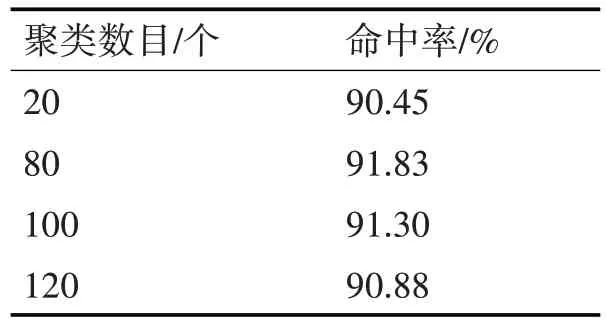
表3 基于替代模型Wasserstein distance的聚类方法的命中率（%）

从表3 得知，在不同的聚类数目下，命中率都相当高且没有太大的变化，说明基于替代模型Wasserstein distance 的聚类方法的聚类效果比较好。

本文将两种方案进行对比，方案一为基于KL散度的聚类方法，方案二为基于替代模型Wasserstein distance 的聚类方法。两种方案都采用423人，信道为固定电话信道，并且设置搜索率为10%，使用的训练语音以及测试语音所用的时长都为1min。所得的两种聚类方案的命中率对比如表4所示。

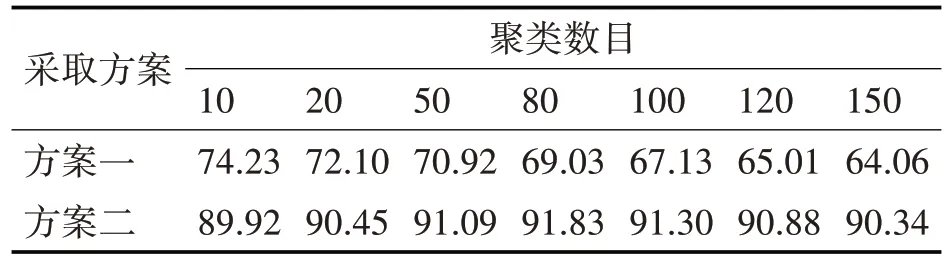
表4 两种方案的聚类命中率对比（%）

从表4 可得，相对于第一种方案，第二种方案聚类效果较佳，并且计算量较小，因此本文选择第二种方案作为说话人聚类所使用的距离定义。

2.4 传统识别与聚类识别的对比

实验在Window10系统下，基于VS2020中MFC框架完成。主机配置为CPU 为Intel（R）Core（TM）i7-9750H CPU @ 2.60GHz，RAM 为32GB。采用的是945 人电话信道下的说话人语音。采用N 阶多元高斯混合模型，其中N 为32。并且训练时长为10s，测试语音也为10s。为了对比传统说话人识别和基于模型聚类的说话人识别的差异，首先要得出传统说话人识别系统下的识别准确率和识别耗时，如表5所示。

表5 传统GMM模型说话人识别系统的识别准确率和识别耗时

聚类后，可以得到在不同搜索率下的说话人识别准确率如表6所示。

表6 不同搜索率下的说话人识别准确率（%）

如表6 所示，在聚类数目一定的时候，从低往高设定递增的搜索率，基于近似模型Wasserstein distance聚类算法的说话人识别的识别准确率总能在搜索率为10%左右时达到峰值，并在达到峰值后再提升搜索率，识别准确率反而下降。这是因为，设定搜索率为峰值所对应的搜索率时，被搜索的说话人模型中正巧包含与测试说话人相对应的说话人模型。在此基础上继续扩大搜索范围，就多增加了不相匹配的干扰项，因此说话人识别的准确率反而降低。本文通过设置不同的聚类数目以及搜索率，可以得出当聚类数目为100 的时候，最佳识别准确率为89.81%。显然，对比传统的说话人识别，在相同的说话人规模、训练语音以及测试语音情况下，基于聚类方法的识别准确率有着较高的提升，即从85.08%提升至89.81%。

另一方面，由于搜索率为10%左右时，识别准确率达到峰值，因此，我们可以获取在同样实验情况下，基于聚类算法的说话人识别耗时以及模型训练的耗时，如表7 所示。并且可以得到传统GMM识别与聚类识别的耗时对比如表8所示。

表7 建模耗时以及识别耗时（s）

表8 传统GMM识别与聚类识别的耗时对比

如表7 及表8 所示，说话人建模与说话人匹配分别需要耗时1845s 与1465s，即聚类后的识别过程一共需要耗时3310s，比起传统说话人识别所需的12984s，识别效率有着显著的提升。

3 结语

本文针对传统说话人识别在大规模说话人规模下的识别准确率下降，以及识别耗时过长的情况，提出了一种基于模型聚类的说话人识别方法，对传统的说话人识别方法进行改进。相比于传统说话人识别方法，该方法的识别准确率提升了近4.7%，并且识别耗时仅为传统识别方法的25.5%，大大提升了说话人识别系统的实用性。