基于梯度提升回归树的高新企业创新能力评估∗
郑泳智 吴惠粦 朱定局 宋东情
(1.华南师范大学计算机学院 广州 510631)(2.广州国家现代农业产业科技创新中心 广州 510520)
1 引言
十八大明确要求,要把创新驱动视为经济发展新的动力源泉,科学技术能力和劳动质量在社会发展中的作用不应孤立地看待,而应联系起来以促进社会进步[1]。
政府政策扶持力度与资金投入对企业创新能力是相关联的。张莉芳[2]根据部分新兴产业数据研究分析也验证了这一观点;胡本田[3]根据数据分析发现政府补助对创新绩效产生直接正向调节效应;Sun J 等[4]以PSM-DID 模型为工具,发现研发费用相关政策的实施对企业创新行为有正向影响。因此审计部门关注企业创新能力发展,并安排相关审计专家根据企业相关业务信息、环境条件、创新投入、创新产出、财务成长等数据,设计不同的创新指标分析企业创新能力变化,为政府部门提供决策依据,优化资金投入结构等。徐立平等[5]归纳总结了九类企业创新能力评价体系,提出其不足之处,尤其是消除人为因素干扰方面存在较大问题。孔祥纬[6]首次提出使用基于支持向量机的方法构建创新能力评分预测模型,虽可消除人为因素影响,但是预测效果存在提升空间。栗晓云[7]提出使用随机森林等算法构建模型预测创新政策对企业创新能力的影响,可有效帮助政府在企业补助等问题上做出决策。因此,依靠机器学习方法对企业创新能力进行评分预测,有利于审计部门分析企业创新能力变化。在微观上,有利于发现其创新能力的不足,为决策者提供依据,加强创新管理,完善创新机制,提高竞争优势。在宏观上,符合条件的创新型企业可受益于政府政策扶助,推动区域繁荣发展并形成区域优势。
预测企业创新能力评分问题,实际上是回归问题。Friedman[8]指出回归的关键在于优化函数,目的是求出因变量关于自变量的函数,使损失函数期望最小。近年来,回归预测广泛应用于各领域,如Pandey G 等[9]提出基于SEIR 和回归模型预测新冠疫情;Quan Q 等[10]提出使用改进的支持向量机结合太阳辐射的水库水温,对我国西部大型高海拔水库的水温进行了分析;Jiang L等[11]提出使用贝叶斯回归模型预测港口吞吐量。
关于企业创新能力预测,作者构建不同预测模型进行实验,实验结果发现传统的单一回归模型存在精度低与泛化性不足等问题。例如,支持向量回归(Support Vector Regression,SVR)、线性回归(Linear Regression,LR)等模型在关于企业创新能力预测问题中,效果均不理想。集成学习[12]为了降低泛化误差,可以将多个个体学习器合并,得到更合理边界,降低整体错误率、提高模型性能[13]。本文提出运用梯度提升回归树(Gradient Boosting Regression Tree,GBRT)算法进行企业创新能力的回归预测,GBRT 属于集成学习算法中的一种,结果表明模型能拟合出与审计组专家评分相似的结果,优于其它模型。
2 集成学习算法
2.1 集成学习
集成学习已遍及各行业各领域,特征选取、回归预测等问题都能见到它的身影。如图1 所示,集成学习依靠某一策略有机组合多个学习器。其中,BP 算法[14]、SVM 算法[15]等学习算法往往会被用于构建个体学习器。而集成学习则通过某种策略将所有个体学习器产生的结果整合,如平均法、投票法、学习法。因此通过集成学习算法构建模型在结果上会比单一模型更加稳定,泛化能力更强。

图1 集成学习原理示意图
主流的集成学习方法按基学习器间独立程度划分为两种类别。即基学习器必须依次生成的Boosting提升算法[16]与基学习器可并行生成的Bagging 装袋算法[17]。除了基学习器间依赖性强弱不同,二者在样本选择和权重调整上也有所区别。Boosting 可根据错误率调整权重使得Boosting 精度往往高于Bagging。
2.2 梯度提升回归树
提升树算法中残差计算较复杂,导致训练速度较低,Friedman 最早提出使用梯度提升回归树GBRT,将损失函数负梯度值表示为残差,以提高训练速度。GBRT 属于Boosting 算法中的一种泛化,近年来广泛应用在各个领域,Samadi等[18]提出利用GBRT 近似分析预测生物质材料较高的热值,效果优于其他模型;Pan 等[19]提出利用GBRT 估算天然气公交车的排放量,为移动等排放模拟工具提供理论支持;Deng 等[20]利用GBRT 预测蛋白质-RNA 结合亲和力,取得较好的效果。
算法1 梯度提升回归树GBRT算法
由式(4)可知树的数量M 和学习率v 影响模型的预测精度。回归树数量M也称为最大迭代次数,设置不当容易出现过拟合或欠拟合;学习率v 也称步长,学习率设置恰当将有利于防止过拟合。回归树数量M 和学习率v 往往需要结合起来调整,其优化过程将在后文进行论述。
3 实验
3.1 实验环境及参数设置
本文实验所用实验环境如表1所示。

表1 实验环境
3.2 实验数据集
实验采用广东省审计厅提供的2016 年度2510家广东省高新企业数据作为训练数据,其中包括企业74 项特征数据和对应的审计专家组评分。专家组评分为各审计专家根据企业数据进行企业创新能力评分后的均值,取值为0~100 的浮点值。部分企业特征如表2所示。

表2 部分企业特征
3.3 数据预处理
本文对企业数据的预处理主要有:1)数据去重。若有相同企业编号的企业数据,则删除。2)数据标准化。按比缩放企业数据,将各类企业数据统一映射同一区间有助于提升训练效率。3)空值填补。样本中存在少量企业数据缺失,使用同一列不为空的数值平均值对缺失值进行填补。
3.4 实验设计
为使GBRT 模型效果更佳,实验一使用平均绝对百分误差(Mean Absolute Percentage Error,MAPE)作为评价指标,通过网格搜索与交叉验证法对超参数进行调整优化,并研究分析超参数对误差的影响。
为验证梯度提升树预测效果由于其他模型,实验二训练Adaboost、Bagging、GBRT、SVM、RF、LR 等模型,记录其误差值并进行对比。其中,本次实验参考当前广泛使用的误差评价指标,选取平均绝对百分误差(Mean Absolute Percentage Error,MAPE)与均方根误差(Root Mean Squared Error,RMSE)作为评价指标。
3.5 实验一结果与分析
GBRT 模型的超参数最大迭代次数M 和学习率v 对模型预测精度有较大影响。实验一设计不同M值与v值,以MAPE作为模型评估指标,结合网格搜索与交叉验证求得最佳M 与v 的组合。不同组合下的预测结果如表3所示。

表3 不同最大迭代次数和学习率下模型的平均MAPE均值
表3中,第一列从20~1000的M值为式(2)中的最大迭代次数,即创建的M 棵回归树。第一行从0.004~0.018 的v 值为式(4)中的学习率,即更新模型的步长。实验利用K 折交叉验证方法进行模型训练K 次,对K 个平均绝对百分误差值求平均,作为超参数调优的评价指标,其中K 取值为10。当M 取值大于600,v取值大于0.014时,随着M 与v值增大,模型效果提升越不明显。当最大迭代次数和学习率分别为1000 与0.14 时,模型效果最好,MAPE均值为6.1113%,优于其他参数组合。
由算法1 可知,调整超参数时,不可以孤立的看待问题,既不能只调整最大迭代次数M,也不能只调整学习率v,否则将陷入局部最优化的困境。实验根据表2数据,画出如图2所示三维图像,以平均绝对百分误差作为Z 轴。可以观察到曲面随着M与v的增长,逐渐收敛为一个平面,平均绝对百分误差无明显变化,即模型效果没有明显提升。当回归树棵树取值为1000 与学习率取值为0.14 时,该超参数组合下训练得到的模型MAPE 值为6.1113%,该模型效果最优。
如图3 所示,实验使用上述最佳超参数组合构建模型后,预测100 个企业创新能力得分。仅有少量预测值与实际值相差较大,如图3中第64个样本值,模型预测效果不理想。大部分预测值均接近于实际值,如图3 中第15 和16 等样本值,均能拟合出与实际值近似结果。因此,GBRT 模型能较好拟合审计专家对企业创新能力的评分。
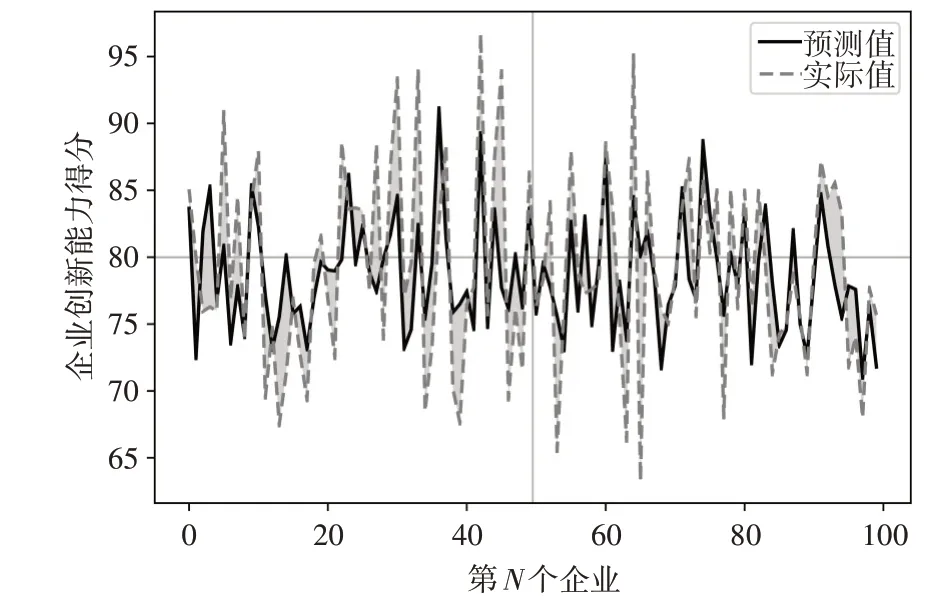
图3 预测值与实际值对比图
3.6 实验二结果与分析
为对比分析不同模型在预测企业创新能力评分问题上的效果,实验二使用AdaBoost、Bagging 等算法进行模型训练,以MAPE 与RMSE 作为模型评价指标,训练集与测试集划分比为4∶1。
如表4 所示,在预测企业创新能力问题上,GBRT 训练得到的模型效果更好,MAPE 达到5.7675%,RMSE 为5.6786,优于其他模型。其中,RF 与GBRT 的模型效果接近,但GBRT 在该回归问题上稍微优胜。其原因在于RF 对异常值不敏感,而GBRT 根据错误率采样,会对异常值较敏感。因此在该回归问题上,对比其他预测模型,GBRT 能更好的拟合审计专家组对企业创新能力的评分。

表4 不同模型MAPE与RMSE对比
4 结语
随着创新驱动发展战略的提出,政府审计部门越来越重视企业创新能力评估,希望通过量化创新能力,发现企业不足之处,协助决策部门调整政策扶持力度与方向,精准提高某区域或某行业的竞争力。但审计专家组根据企业相关数据评估企业创新能力的工作量较大,同时容易出现误判,为提高审计厅对企业创新能力的评估效率与能力,本文提出使用GBRT 算法构建企业创新能力得分预测模型,借助GBRT 具有对输出空间中离群点的鲁棒性等优点,拟合出于审计专家组相似的评分效果。经过验证,该模型效果优于Adaboost等五类算法构建的模型。

