基于机器学习的河湖底泥机械脱水效果试验

曾嘉辰,白 鹤,王 盛,郭 兵,严晓威,郝宇驰

(中交疏浚技术装备国家工程研究中心有限公司,上海 200082)

随着国家对于河湖整治工作的不断推进,越来越多的河湖治理技术与设备投入使用,其重点难点均在于河湖底泥的脱水固化环节,了解泥质特性、脱水药剂添加量与河湖底泥脱水固化效果之间的关系几乎成为河湖整治工作中的必要前提[1-3]。

目前,有关泥质特性、脱水药剂添加量与河湖底泥脱水固化效果之间关系的获取方法主要有两种。第一种是基于物理模型试验的现场验证方法[2,4],其在理论方法的基础上通过室内试验得到相关评价参数值,并依此来对各项试验参数进行评价,能够较为准确地评判各项试验参数之间的内在联系,但是该过程需要设计合理的试验参数范围,且存在误差的情况,具有周期长、效率低的劣势[5]。第二种是基于大数据的机器学习预测模型[6-7]。机器学习作为人工智能中最具智能特征、最前沿的研究领域之一,可以依据已有的数据或经验,得到某种模型,并利用此模型对未来进行预测。机器学习已在大气监测[8]、水污染监测[9-10]以及加药控制等多领域得到广泛应用[11]。但利用机器学习技术在河湖整治技术过程中的研究较少。除此之外,近年来诸如BP神经网络[12]、符号回归等方法成为在解决实际工程领域相关问题的热点。以往针对药剂投放量的预测模型大多基于多元线性回归方程,此种方法需要给定拟合变量及公式,使得经验公式的预测性能往往要受限于人为主观因素,不利于全面准确地评估泥浆含水率、药剂投放量等参数对泥浆脱水固化性能的影响。而神经网络模型是一种具有非线性适应性信息处理能力的算法,可克服传统人工智能方法对于直觉,如非结构化信息处理方面的缺陷,具有较强的非线性映射能力[13]。符号回归作为一种监督学习方法,试图发现某种隐藏的数学公式,以此利用特征变量预测目标变量,可以不用依赖先验的知识或者模型来为非线性系统建立符号模型。

本文根据试验相关数据,采用BP神经网络和符号回归两种方法对不同药剂投放量对泥浆机械脱水性能进行系统地评估,以得到更加科学准确的泥浆脱水固化性能的预测方程。

1 材料与方法

1.1 数据来源

本研究数据依托厦门某湖综合整治项目,如表1所示,样品源自绞吸船及气动泵船施工区域不同深度的柱状取样器。取样区域1、区域2、区域3分别为厦门某湖由西向东的3个不同片区,S1-1、S1-2、S2-1、S2-2、S3-1、S3-2分别为各区域取的平行样品,泥质呈现黄褐色、黑灰色、深黑色3种,伴有陈腐气味。针对底泥脱水干化厂区中初沉池中的泥浆,即经过稀释的原状土,含水率在10%～15%,开展的污泥比阻试验及模拟板框压滤试验,得到不同加药量下的各类经验数据(表2)。

1.2 研究方法

1.2.1 BP神经网络模型

BP神经网络模型[7]是目前为止应用最为广泛的模型之一,其网络结构如图1所示。

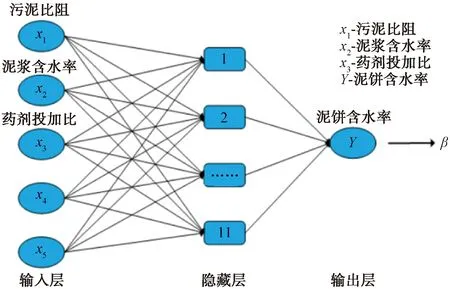
注: β即代表最终值,x4～x5为其他可对含水率产生影响的参数,本次试验未涉及。

BP神经网络模型是一种误差反向传播训练的多层前馈网络,其算法称为BP算法,基本思想是梯度下降法,即利用梯度搜索技术,不断调节权值与阈值,使预测值与实际值间的误差达到最小[11]。输入层和输出层的神经元个数要分别与输入和输出变量个数相同,选取的输入参数有泥浆含水率A、药剂投加量B和污泥比阻C,选取的输出参数为泥饼含水率D。对于BP神经网络,其输入和输出层的节点数是由输入与输出参数决定的;而隐藏层的神经元个数则受输出结果的精度控制。隐藏层中神经元数量太少会产生欠拟合现象,而太多则会导致过拟合。确定隐藏层神经元个数时,通常先根据经验公式[式(1)～式(2)]来确定隐藏层神经元个数的大致取值范围,然后通过对不同神经元个数下神经网络的训练效果进行比较,找到误差最小的神经元个数[12]。

(1)

(2)

其中:nI——输入层神经元个数;

m——输出层的神经元的个数;

nh——隐藏层神经元个数[12];

a——[1,10]的常数;

k——训练样本数量。

综合本文研究内容,设置nI=3,m=1;最终确定隐藏层神经元个数为9,激活函数采用Tansig函数,可以较好地解决Sigmoid函数收敛变慢的问题[13],相对于Sigmoid函数而言提高了收敛的速度。输出层神经元个数为1,激活函数采用线性函数。训练算法选取Levenberg-Marquardt算法,该收敛速度较快[14],能够有效处理冗余参数问题[15]。

1.2.2 符号回归模型建立

遗传编程的运行流程如图2所示,首先要用户给定函数符集和终止符集,随后由函数符集和终止符集随机产生初始种群。其次,基于适应度评价标准,对种群中个体的适应度进行评估。最后,初始种群通过执行遗传操作(交叉、变异及复制等)产生新种群,直至满足预设的终止条件。作为回归分析的一种,符号回归(symbolic regression)也称为函数建模或函数辨识,是遗传编程最早的一类应用之一。它搜索数学表达式的空间,找到最适合给定数据集的模型,无论是在精确性还是简单性方面,能够针对目标问题进行自主建模[16],无需主观假设公式形式;其通过训练给定样本数据集,来探索隐藏在试验数据随机性背后的内在规律,从而确定和分析目标问题中各变量之间的函数关系。搜索过程遵循达尔文的自然选择原理,利用计算机程序模拟基因复制、交叉和突变等操作,在初始群体数量较大且设置合理交叉、变异概率的情况下,最终结果不会陷入局部最优解。该模型不需要模型的先验规范,因此,不会受到人为偏差的影响,也不会受到领域知识空白的影响。

2 结果与讨论

2.1 试验分析

2.1.1 泥质分析

厦门某湖各阶段底泥的沉降性能和滤过性能均较差,特别表现在SV30指标和CST指标。SV30在69%～99%,属于沉降性较差,自由水含量低的泥浆。但含水率情况来看,区域1含水率约为38%,区域2含水率约为46.98%,区域3含水率平均值为48.61%,表明底泥成分中可能含有大量砂质。3个区域的底泥CST在92～236.7 s,CST值越小,污泥脱水性能就越好,属于较易脱水的泥性。絮凝物的表面电荷是影响絮体聚集和脱水性能的关键因素之一。通常用Zeta电位来表征底泥的表面电荷,根据DLVO理论,Zeta电位的绝对值越大,絮体间的静电斥力就越大,污泥就越难以絮凝和沉降[6]。经化学调理后,随着絮体间的静电斥力急剧减小,污泥就更容易絮凝和沉降,脱水性能显著提升。厦门某湖各阶段底泥的Zeta电位完全呈负电性,且除区域3-3外绝对值均偏大,最高绝对值为区域1-1(3.56 mV),表明底泥的沉降性能和过滤性能都较好。

2.1.2 脱水效果分析

通过污泥比阻试验及模拟压榨试验对疏浚泥浆进行最优投加量选型。选取泥浆浓度为常规生产浓度,即15%左右,试验使用的药剂为阴离子PAM,相对分子质量为1 500万Da。PAM是分子所带电荷能够能起到中和污泥颗粒所带电荷的作用,使污泥颗粒与水分子分离,絮凝成大颗粒污泥,改善污泥性能[6]。结果显示,随着药剂量的提升结合污泥比阻、泥浆调理情况及泥饼含水率来看,药剂最优添加量并非完全受泥浆浓度控制,受泥质影响,总体呈现随着浓度梯度上升,加药量升高趋势,但也存在含固率15%泥浆浓度(质量分数)下,加药量翻倍的情况,在低浓度情况下,最佳加药量在0.04‰～0.08‰。如表2所示,在15%的泥浆浓度(质量分数)下,污泥比阻和泥饼含水率并非呈现正比关系,随着PAM药剂浓度上升,污泥比阻值与泥饼含水率总体趋势为下降状态,污泥比阻值在1.0‰和1.1‰下有明显下降,泥饼含水率在1.0‰、1.1‰以及1.2‰ PAM投加量下有明显下降。总的来说,受泥浆含水率和泥浆内部成分影响,泥浆在2.0‰ PAM的投加量下比阻值和含水率(36.49%)最低,要获取泥浆含水率、污泥比阻、加药量与泥饼含水率之间的关系需要进一步的科学建模来进行预测。

2.2 模型建立

2.2.1 BP神经网络

现将所获得数据经过试验结果分析,划分特征值与标签值,通过划分函数随机切分为训练数据集与测试数据集,随机选取80%作为训练数据集,20%作为测试数据集。训练集的输入参数代入已建立的BP神经网络模型中。图3给出了BP神经网络预测结果和实测结果之间的对比。当滤饼含水率处于32%～53%时,BP神经网络的预测值离散误差相对较大,但是基本都均匀分布在理想线y=x两侧,并大部分在±20%的误差线以内;当滤饼含水率大于53%时,训练集数据基本分布在±10%的误差线以内。由此可以看出,训练集的预测值和实测值有较高的相关性,BP神经网络对该训练集有较好的预测效果[17]。

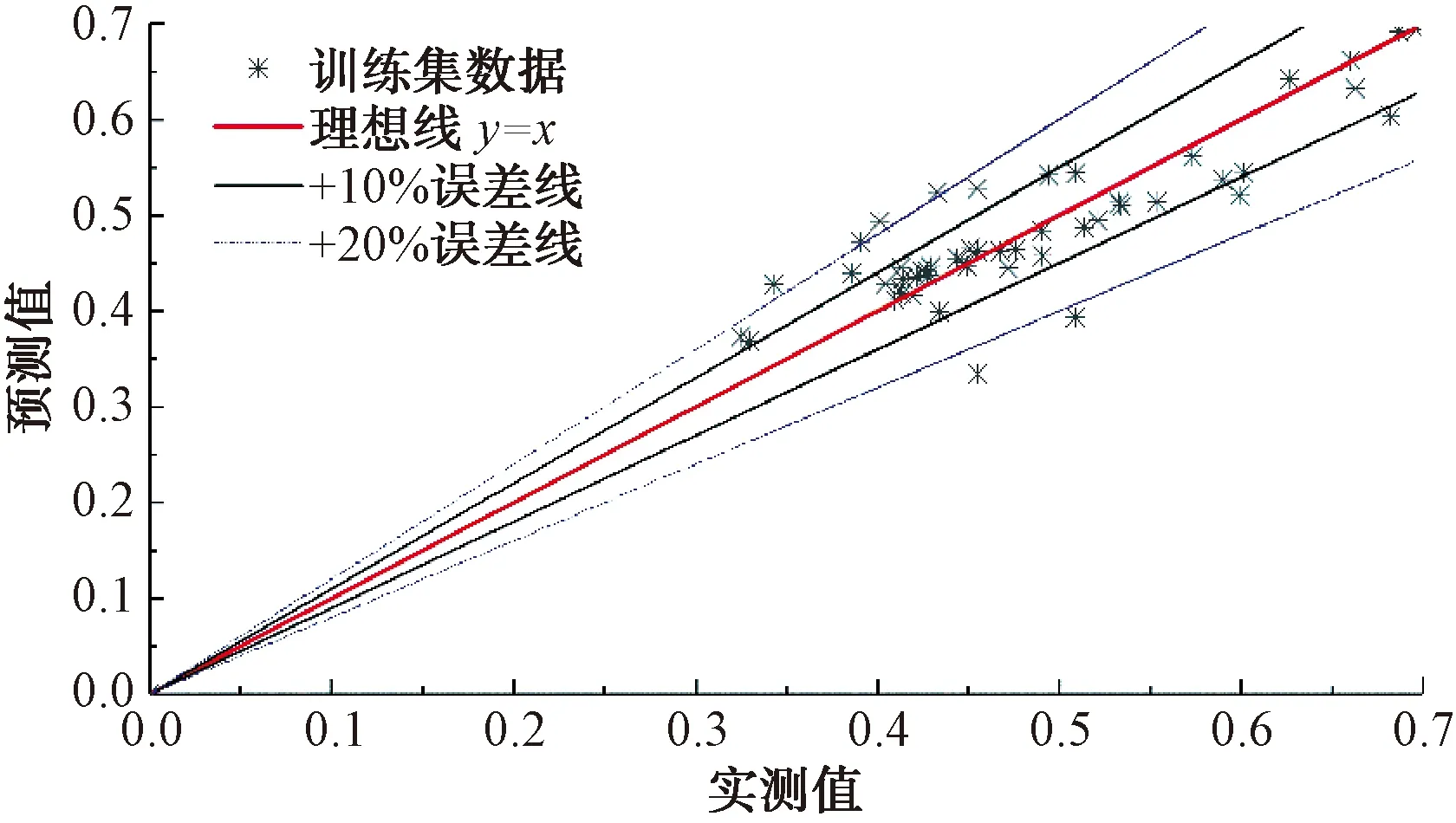
图3 BP神经网络预测结果和实测结果之间的对比

为进一步验证上述模型预测的滤饼含水率的能力,现将未参与训练的测试集数据带入上述建立好的BP神经网络模型,图4给出了测试集的预测值与实测值之间的对比图。由图4可知,大部分数据点均在±20%的误差线以内,90%的数据处于±10%的误差线以内。以上测试集数据的验证表明本节构建的泥浆脱水固化后滤饼含水率的BP神经网络模型具有较高的精度。

图4 BP神经网络测试集的预测值与实测值之间的对比

基于BP算法建立的模型,得到上述预测值与实测值的对比结果,可以得到较好的预测结果,但是无法得知各输入变量敏感性的强弱。因此,本文引入平均影响值(mean impact value,MIV)来评估模型输入参数对输出结果的影响程度。MIV的计算方法是:基于训练好神经网络模型,将某个输入参数的样本量分别增加和减少10%(其他输入参数保持不变),将两组数据输入模型,然后通过对比两组数据的输出结果求得该参数的MIV。为更加直观地评估每个输入参数对出的贡献程度,图5给出了各输入参数MIV占比的饼状图。污泥比阻参数的MIV占比最高,达到48%;其次是泥浆含水率为46%,药剂投放量占最小比重,为6%。根据结果表明,泥浆污泥比阻特性对脱水固化效果影响最大。

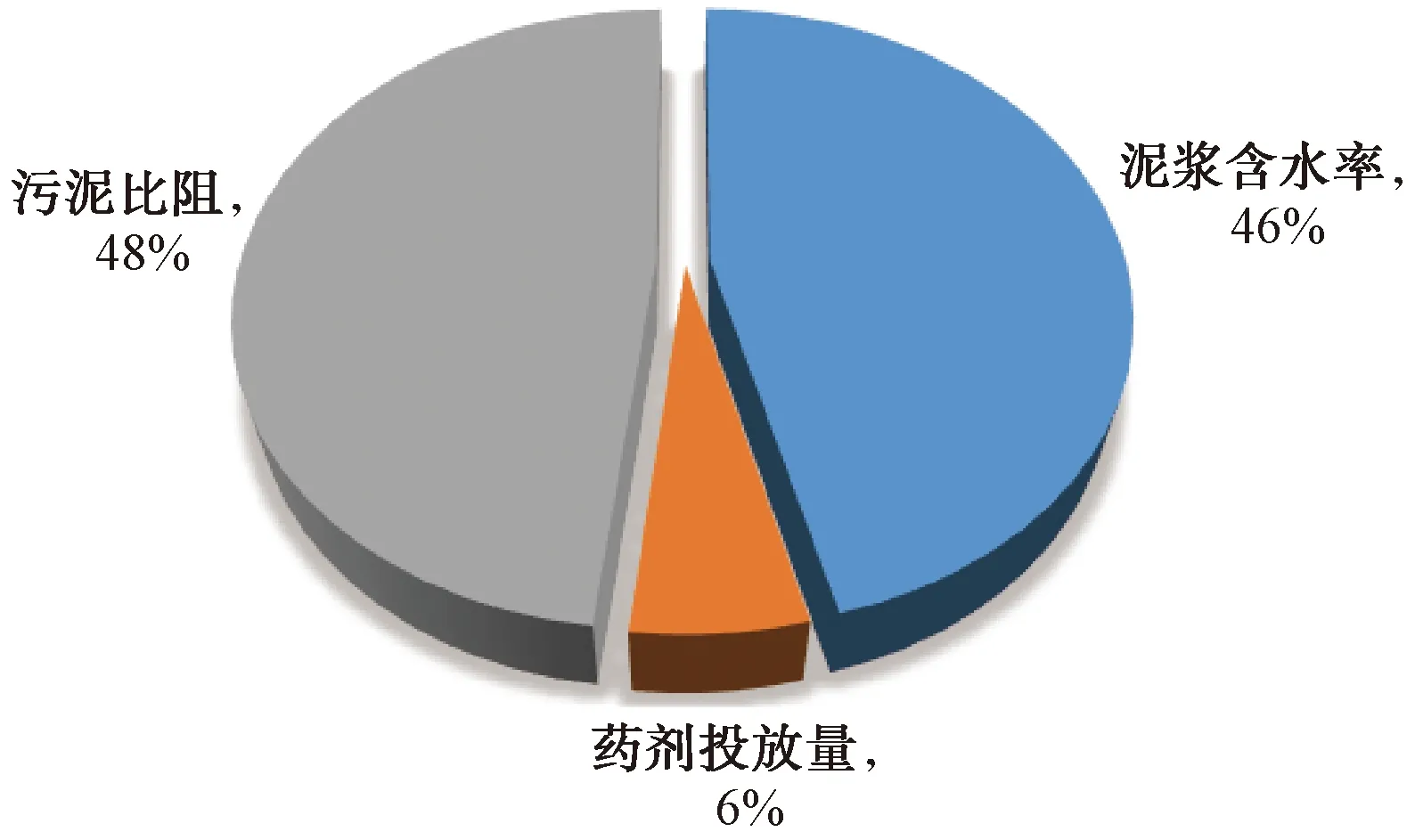
图5 不同参数MIV分布

2.2.2 符号回归模型结果

借鉴前人研究[2]中符号回归方法的成功应用案例,本文利用基于遗传编程算法[3-4]的进化搜索来确定以相对简洁形式描述数据集内在规律的函数关系式的符号回归计算机程序。首先将训练集数据输入,代入公式进行评估后,共有16个候选方案经过“优胜劣汰”的自然选择后得到。表3给出了各候选方案的公式表达式,各公式所对应的最小和最大复杂度分别为1和53,对应公式的适应度函数评价指标平均相对误差(MAE)、均方误差(MSE)和相关系数(R2)同时在表中给出。随着公式复杂度的增加,MAE、MSE相应减小,R2增大。公式形式最复杂的方案(即复杂度为53)应该是预测滤饼含水率最好的公式,但其过于复杂,故不予过多考虑。最终选定复杂度为26[式(14)]的为最优方案。

图6给出了描述候选方案误差MAE和复杂度之间关系的帕累托前沿图,通常利用帕累托前沿图评估各候选方案的MAE和复杂度之间的关系,进而确定最优方案。由图6可知,当复杂度在[1,16],随着复杂度的增加,候选个体的MAE值相应减小;而当复杂度在[15,26],MAE衰减速率逐步变缓;且当复杂度大于26时,候选方案复杂度的大幅增加只会导致MAE的小幅减小,即增加公式复杂度并不会大幅提升模型预测精度。

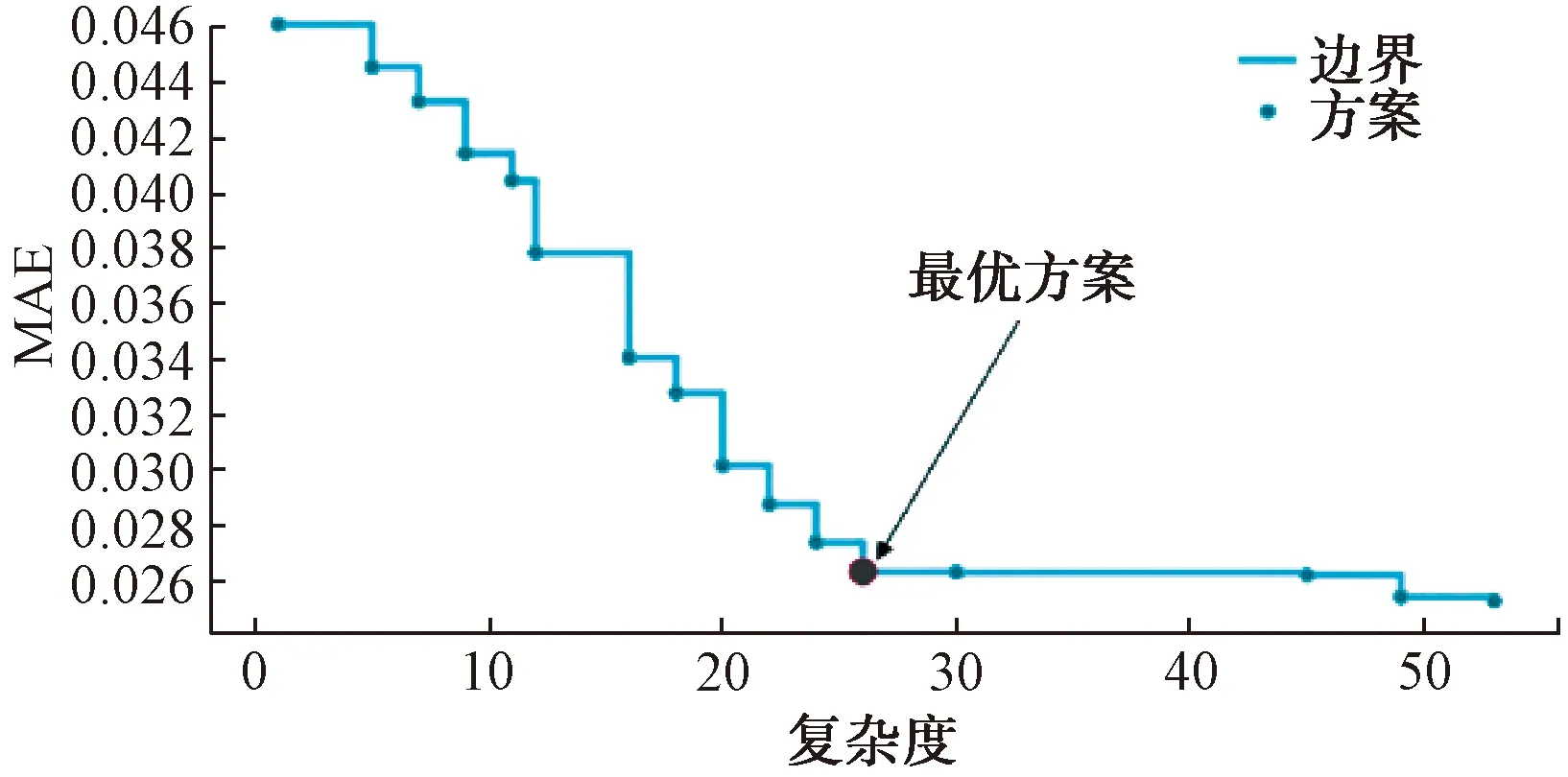
图6 误差MAE和复杂度之间关系帕累托前沿图

将训练集数据输入参数代入上述选定的符号回归模型进行计算,得到的预测值与实测值如图7所示。由图7可知,在滤饼含水率为35%～55%时,预测值与实测值误差较小,模型的预测精度较高;总体上,80%以上的数据相对误差小于20%,说明模型预测结果在一定范围内是可靠的。

图7 符号回归模型训练集实测值与预测值对比

为进一步验证复杂度26[式(14)]的预测精度,将未参与训练试集数据代入所选定的模型公式,图8给出了测试集的预测值与实测值对比。可以发现,大部分测试集数据均在10%的误差以内,90%的数据误差均在20%以内,预测值与实测值之间总体吻合较好,结果相对可靠,说明所选的模型公式具有一定的参考意义。

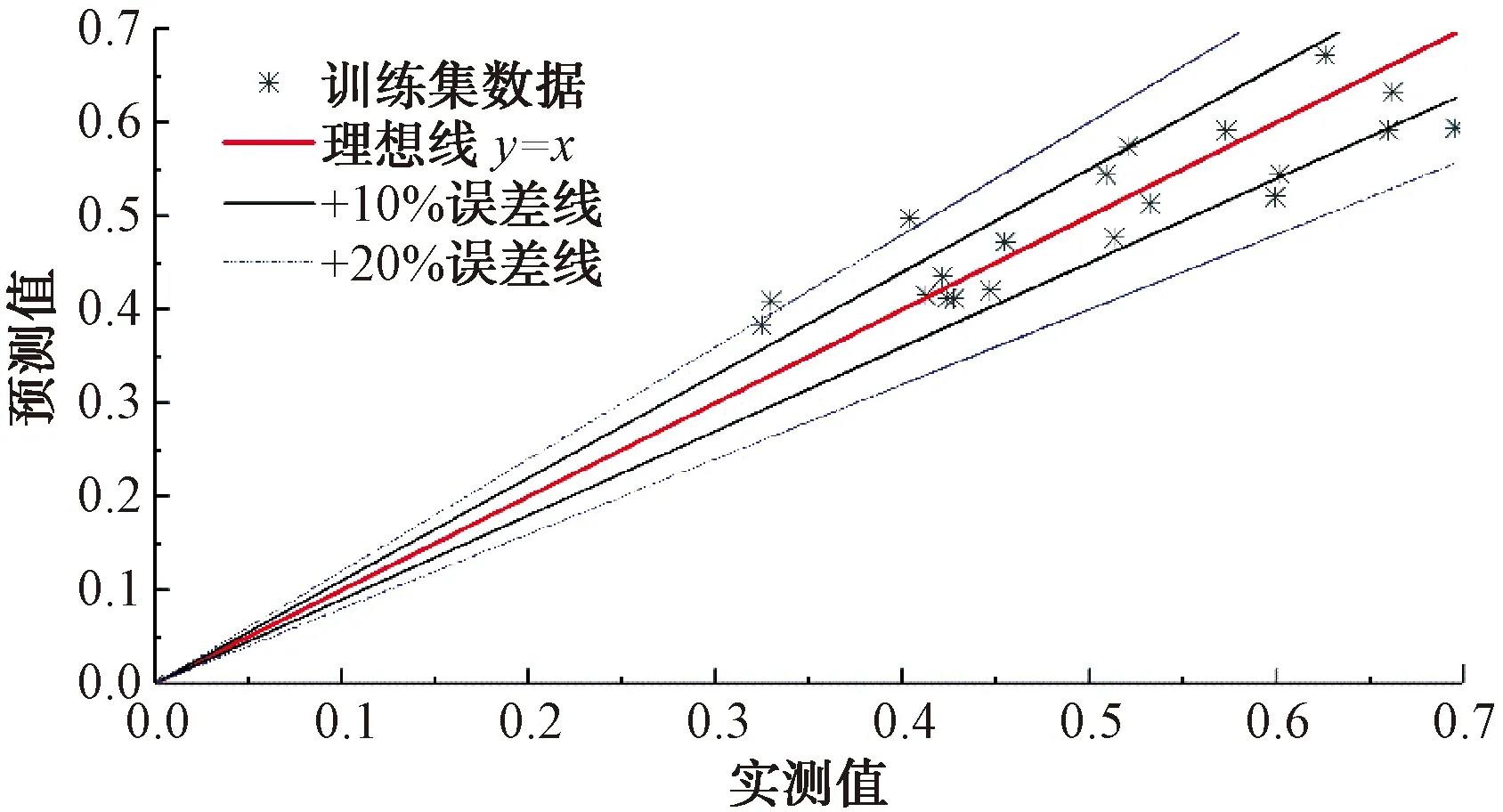
图8 符号回归模型测试集实测值与预测值对比

对于符号回归模型中各输入参数的重要程度,通常通过某一输入参数在所有候选方程中出现次数与出现该因素的候选方程数来评估该参数重要性。由图9可知,其中泥浆含水率出现的次数最多,随后是污泥比阻,药剂投放量最少。这与上述神经网络得到的结果较为相似,影响滤饼含水率的重要参数为含水率和污泥比阻,同时根据试验也能发现,投放药剂能够加速泥浆脱水,最终滤饼的含水率主要由泥浆自身特性控制。

图9 符号回归模型中各参数重要性评估

2.3 BP神经网络和符号回归方法分析对比

两种模型对比为进一步定量评估3种模型的预测性能,本节引入4种常用的误差评价指标,包括MAE、平均相对误差(mean relative error,MRE)、MSE及均方根误差(root mean square error,RMSE)。

表4给出了BP神经网络和符号回归模型间不同误差指标的大小。两种模型的各项误差指标存在一定的差异,BP神经网络模型预测结果的所有误差指标均小于符号回归。BP神经网络方法下,MRE和RMSE值分别为0.088 2和0.035 4,符号回归方法下,MRE值和RMSE值分别为0.089 7和0.047 2。因此,对于本项研究,BP模型对未知数据具有更好的模型选择能力以及对未知数据具有更好的泛化能力和鲁棒性[18-19],而符号回归模型在此方面的能力较弱。

表4 BP神经网络和符号回归模型间不同误差指标

3 结果与讨论

本文基于机器学习方法(BP神经网络和符号回归方法),建立了泥饼含水率的预测模型,得到以下结论。

(1)本文以现场室内试验数据为研究基础,采用随机选取的方法将样本数据划分为训练集以及测试,模型构建与验证。结果发现两种机器学习方法所建立的预测模型的精确度良好,具有一定的可信度。总的来说,80%以上的数据相对误差小于20%。

(2)基于BP神经网络和符号回归方法建立的预测模型后,对两种模型的输入参数对输出参数贡献程度进行比较发现,两种预测模型结果相似。其中泥浆含水率和污泥比阻对泥饼含水率影响程度差异不大且均较大,加药量影响较小。这是由于加药量能够加速泥浆脱水固化,对最终的泥饼含水率影响较小。

(3)针对MAE、MRE、MSE及RMSE 4种常用的误差评价指标,对3种预测模型进行定量分析对比,发现BP神经网络预测精度高,神经网络预测精度高,MRE值在0.088 2,RMSE为0.035 4,并且在泛化能力和鲁棒性上也表现良好。