强震下不同站桥组合体系抗震性能对比研究

焦驰宇，任 超，刘能文，秦永刚，程冕洲

（1.北京建筑大学工程结构与新材料北京市高等学校工程研究中心，北京 100044；2.北京建筑大学未来城市设计高精尖创新中心，北京 100044；3.北京建筑大学大型多功能振动台阵实验室，北京 100044；4.北京市市政工程设计研究总院有限公司，北京 100082；5.中国建筑设计研究院有限公司，北京 100044）

引言

近年来，随着中国交通建设快速发展，城市轨道交通运营总长度迅速增长。截止2021 年，轨道交通运营里程达8736 km［1］。这些导致城市核心区域可利用建设用地日益紧张，建设者须对有限的空间资源进行高效整合利用，以期获得更好的城市开发综合效益，因而轨道交通的发展趋于立体化，站桥组合体系逐渐成为城市轨道交通建设的首选。

中国大量区域位于亚欧板块和太平洋板块交接地带，地震异常活跃。桥梁作为交通线的重要组成部分，在地震灾害发生时要求使用功能不受影响或有限受损但可尽快恢复使用。同时现有规范［2-3］表明，普通地铁车站结构属于抗震设防烈度为乙类的重要公共建筑，往往人员密集，在地震等灾害发生时应确保结构安全，保证人员疏散和逃生，其抗震安全尤为重要。采用不同站桥组合体系的结构形式因土、地铁、桥梁结构间传力路径不明确，其在强震作用下是否产生桥梁与地铁结构间的动力耦合作用尚不清楚。因此结构损伤位置和损伤程度难以综合判断，其抗震性能成为设计中亟待解决的研究命题。

近年来国内外对站桥组合体系抗震性能研究已经取得了一定的进展。陈雷等［4］对站桥合一结构进行了数值模拟分析，发现地铁站与桥梁合建会导致桥梁基频减小，桥梁内力分配模式也会随之改变；董城等［5］对某轻轨铁路站桥整体结构进行数值模拟分析，提出在分析时要充分考虑站桥组合结构荷载组合的特殊性，以保证结构安全性；倪永军等［6］基于有限元软件MIDAS/Civil 与SAP2000 建立了某站桥合一结构的数值模拟简化模型，验证了其合理性和可靠性，并对站桥合一结构的塑性评估方法做了比较分析；Zhao 等［7］对某站桥合一结构进行缩尺振动台试验，并根据结构在不同烈度振动下的损伤提出了一种结构抗震性能评估方法；王轶等［8］在自振特性分析的基础上，采用反应谱法和时程分析法分别研究站桥合一结构在小震、中震及大震作用下的动力响应；郭向荣等［9］对某一高架车站桥梁动力响应的影响参数进行研究分析，并对减小车站结构的站台层和站厅层动力响应提出了合理建议；李静园［10］根据实际工程对某站桥合一结构进行静力与动力分析，并对该结构设计提出相关建议；李忠献等［11］的研究表明，按照现行抗震设计规范设计的车站-桥梁结构组合体系在地震作用下安全性较低，提出在这种组合体系的抗震设计中必须按照组合体系所在地的地震动参数对组合体系进行整体时程分析；董沂鑫等［12］分析了站桥分离结构中地铁车站主要构件的受力特点，在此基础上提出了一种站桥分离结构设计方案；胡显鹏［13］设计了一种新型站桥分离结构用于实际工程，有限元分析结果表明该结构安全可靠，传力路径清晰。

综上所述，国内外关于站桥组合体系多限于对某种典型结构在弹性阶段开展静、动力分析研究，往往缺乏在综合考虑墩柱非线性和基础摩擦滑移非线性相互影响下，针对不同结构体系的抗震性能的对比研究。

基于此，本文依托某工程结构项目，分别建立站桥合一结构与站桥分离结构的三维非线性动力有限元模型，综合考虑了桥墩非线性力学行为及站桥分离结构中桥梁扩大基础在地铁顶面砂石垫层上的滑移过程，在此基础上采用时程分析法对比分析两种结构形式各主体受力构件的抗震性能与损伤破坏机理。

1 工程概况

本次站桥组合体系研究以某地铁车站及上部桥梁结构为研究对象。下部地铁车站为双柱三跨地下双层框架结构，车站长度140.80 m，宽24.70 m（8.35 m+8 m+8.35 m），高15.64 m（底层高8.51 m，上层高7.13 m），采用C40 混凝土。地铁站主体采用明挖法施工，每层地铁站间设置双排支撑柱，支撑柱为圆形钢筋混凝土结构。上部桥梁结构长127.19 m（36.24 m+54.71 m+36.24 m），宽17.00 m。桥梁上部结构为两联三跨变截面连续钢箱梁，采用Q345钢材；下部结构为双柱系梁墩，采用C40 混凝土。实际结构中桥梁存在纵坡、墩高不等的情况。本文考虑主桥部分共有4 根桥墩，每个桥墩下端设置扩大基础，坐落于车站顶板之上。其中最低墩及最高墩与主梁通过活动支座连接，下称活动墩；次低墩及次高墩与主梁通过固定支座连接，下称固定墩。桥墩下设置扩大基础，并通过级配砂石垫层与地铁站顶板接触，将上部桥梁荷载分散后传递至下部结构。主体结构纵断面和横断面图分别如图1，2 所示。

图1 主体结构纵断面图（单位：mm）Fig.1 Vertical section of main structure（Unit：mm）

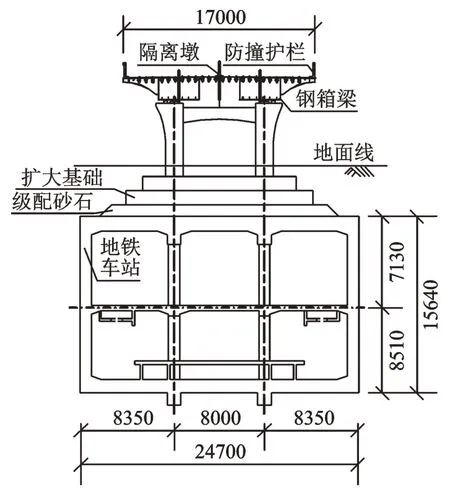
图2 主体结构横断面图（单位：mm）Fig.2 Cross section view of main structure（Unit：mm）

2 有限元计算模型

2.1 模型建立

站桥合一结构与站桥分离结构，其区别在于桥梁扩大基础与地铁站顶板连接方式不同。如图3，4所示，站桥合一结构车站顶板和桥梁基础固结，相当于组合梁结构，桥墩通过承台直接将内力传至地铁车站顶板与支撑柱；站桥分离结构中下部车站与上部桥梁分离，两者间通过砂石垫层接触，层间剪力以摩擦力的形式传递。

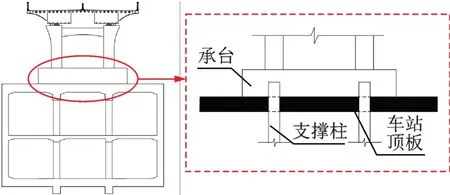
图3 站桥合一结构示意图Fig.3 Structural diagram of station bridge integration

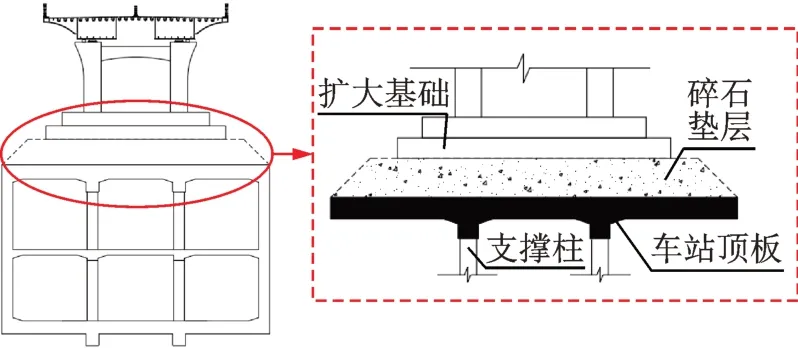
图4 站桥分离结构示意图Fig.4 Structural diagram of station bridge separation

采用通用有限元分析软件MIDAS/Civil 建立站桥合一结构与站桥分离结构的三维非线性有限元动力学模型，如图5 所示。为了方便计算，模型只考虑地铁和桥梁的主体受力结构，忽略了引桥及车站内部附属结构构件及其与相邻结构的相互作用等因素的影响。

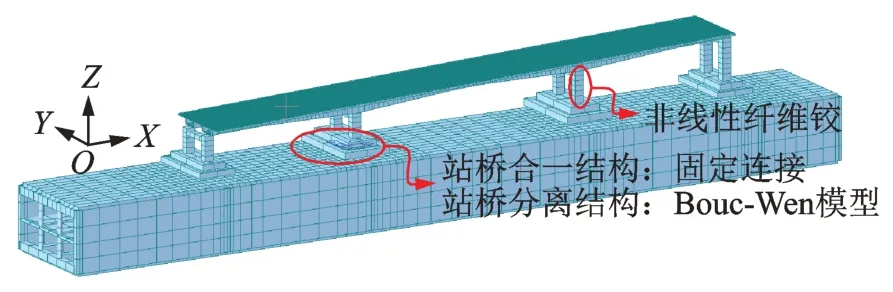
图5 站桥组合体系有限元模型Fig.5 Finite element model of station bridge composite system

本次数值模拟中材料具体参数如表1 所示。桥梁结构的主梁、桥墩以及地铁站结构的横梁、纵梁和地铁柱采用梁单元进行模拟；地铁站结构与桥梁扩大基础具有显著的空间效应，对地铁站楼板、墙体以及扩大基础采用板单元模拟［14］。

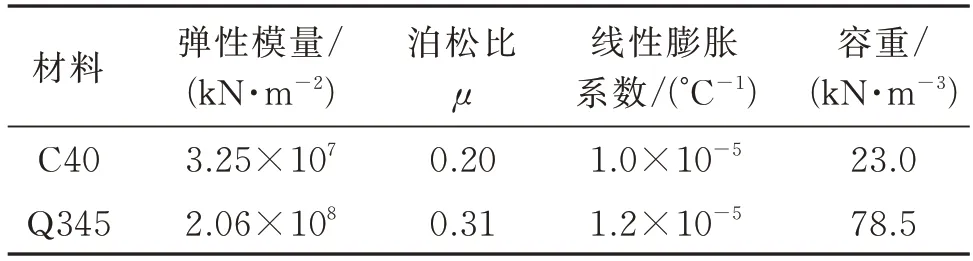
表1 材料参数Tab.1 Material parameters

在地铁车站侧墙和底板对称布置“土弹簧”以模拟土体与结构间的相互作用，所有“土弹簧”在整体坐标系下，设置SDx，SDy，SDz方向的刚度，结合实际工程土层性质，采用《公路桥涵地基与基础设计规范》中的m 法进行“土弹簧”刚度计算，具体如表2所示。

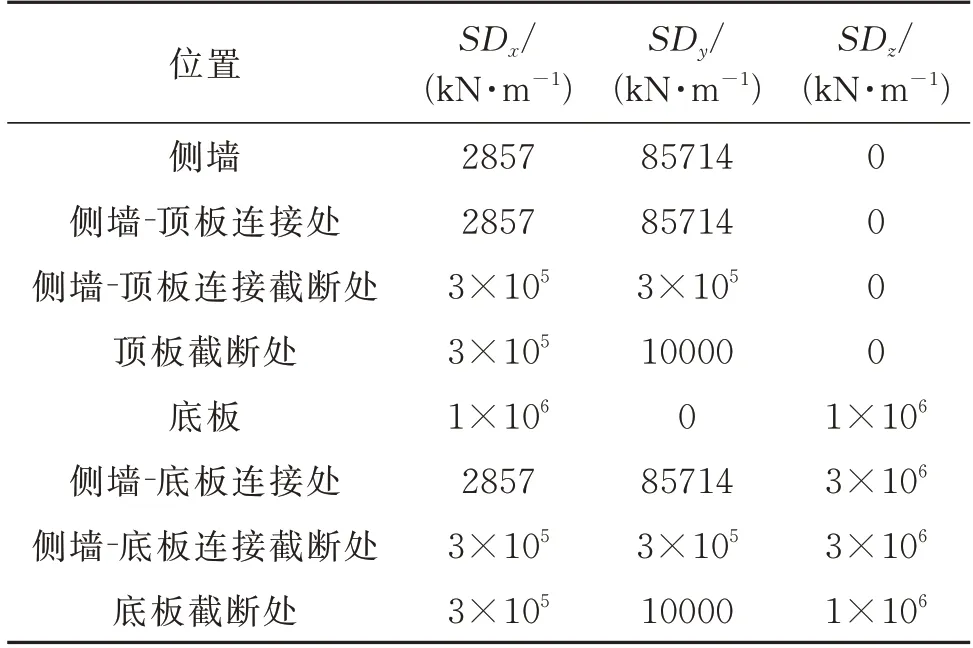
表2 “土弹簧”刚度参数Tab.2 Stiffness parameters of “Soil spring”

同时在桥墩采用非线性纤维梁柱单元模拟桥墩在地震中的非线性力学行为，塑性铰布置及截面纤维分割如图6 所示。

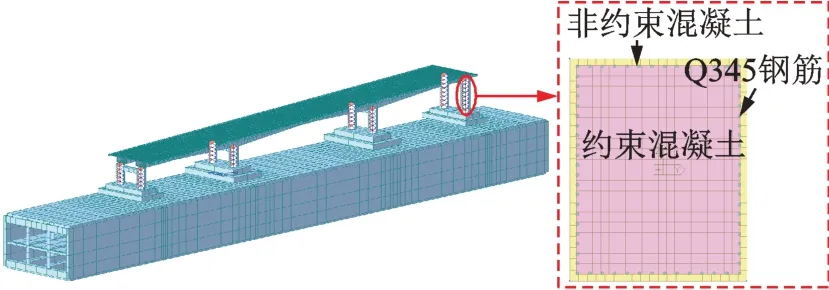
图6 塑性铰示意图Fig.6 Schematic diagram of plastic hinge

地铁车站为地下结构，受力分布较为复杂，本次研究在数值模拟时考虑地铁车站最不利荷载情况，如图7 所示，在地铁车站结构顶板施加均布面荷载模拟上部覆土压力，在侧墙施加三角形分布面荷载模拟土压力，在中板施加人群及设备均布面荷载。在上述荷载作用下，考虑恒载受力情况；考虑中板及顶板附加荷载在地震中产生的惯性力对结构的影响，在时程分析中将该部分附加荷载等效为附加质量，如表3 所示。

表3 地铁车站荷载Tab.3 Metro station load

图7 地铁车站荷载示意图Fig.7 Load diagram of metro station

2.2 垫层模拟

站桥合一结构与站桥分离结构区别在于桥梁扩大基础与地铁站顶板连接方式不同。站桥合一结构中地铁站与桥梁为一整体，桥梁扩大基础与车站顶板间相互作用通过固定连接方式模拟。

站桥分离结构中桥梁与地铁车站间通过砂石垫层接触，其力学行为符合库伦摩擦力学假定，即在基础发生滑移之前，全部水平地震力通过砂石垫层以静摩擦力的形式在桥梁结构与地铁车站结构间传递，此时站桥分离结构的力学行为类似于站桥合一结构。基础发生滑移之后，水平地震力仅以结构与砂石垫层间的滑动摩擦力的形式传递。假定滑动摩擦力等于最大静摩擦力且在基础滑移过程中不发生变化。

通常将上部结构-扩大基础-砂石垫层简化为考虑滑动摩擦作用的多自由度质量、阻尼及弹性振动体系，以等效弹簧、阻尼器模拟砂石垫层，并考虑滑动摩擦作用，其简化动力模型如图8 所示［15］。

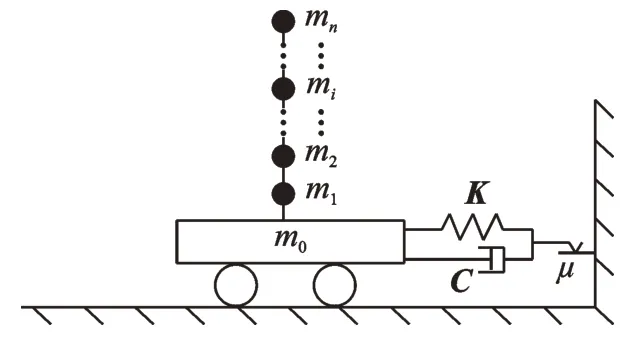
图8 基础滑移结构运动简化模型Fig.8 A simplified model for the movement of sliding foundation structures

根据上述简化模型建立如下结构动力学方程：

式中X为上部结构相对于垫层的位移；M为结构质量矩阵；C为结构阻尼矩阵；K为结构刚度矩阵；为地面水平加速度；f为垫层滑动摩擦力，由下式计算：

式中μ为摩擦系数；m为上部结构整体质量；sgn(⋅)为符号函数。

结构与砂石垫层间的摩擦系数主要由基础混凝土强度、砂石垫层的材料性质以及基础底面的光滑程度确定。有关研究表明摩擦系数可根据由碎石极限应变2%时对应的水平剪力计算，其值如表4 所示［16］。为简化分析，本次研究根据实际工程砂石垫层级配性质确定最终的摩擦系数为0.5。

表4 扩大基础底板与级配垫层间摩擦系数Tab.4 Friction coefficient between enlarged foundation slab and medium sand

结合已有研究及以上对于其传力特征的分析，双线性模型更符合基础滑移结构的恢复力模型。故对以前学者采用轴压弹簧加水平限位装置的模拟方法［17］进行优化，采用Bouc-Wen 弹簧模拟桥梁扩大基础-砂石垫层-地铁站顶板间滑移前后的相互作用，Bouc-Wen 弹簧在水平方向上可设置两阶段刚度，这一力学特性可用于模拟出地震时的基础滑移行为，其力学模型图［18］与恢复力模型如图9 所示。

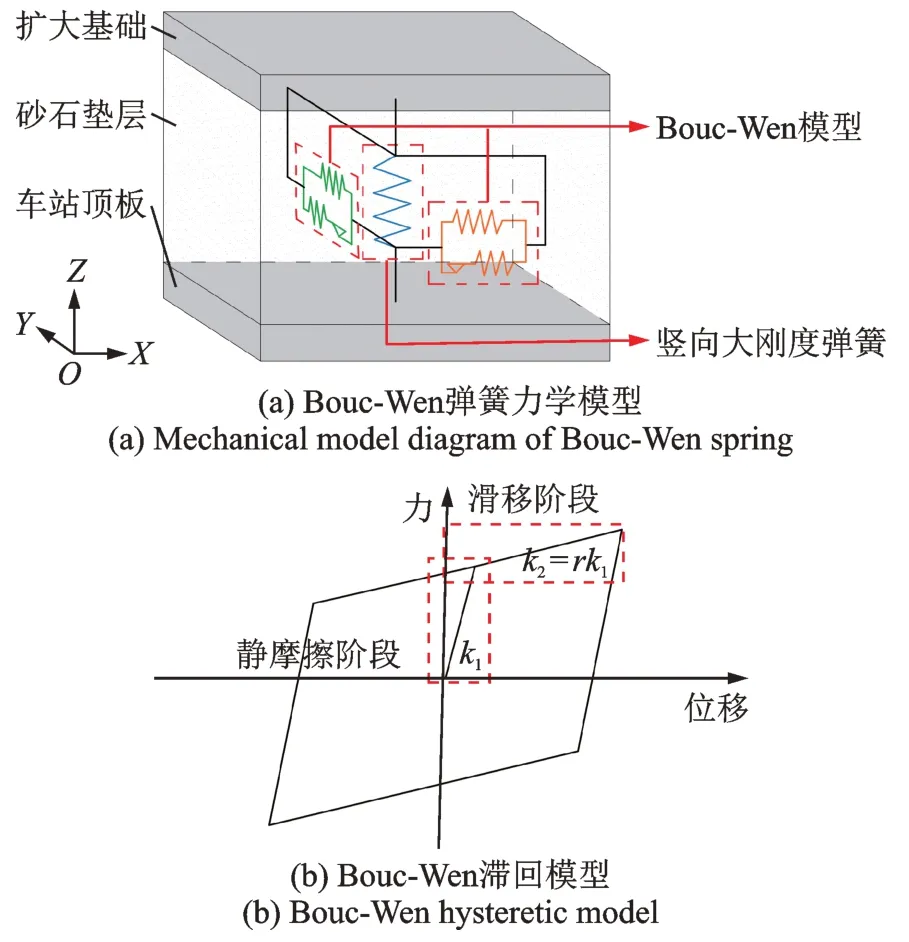
图9 Bouc-Wen 弹簧力学特性Fig.9 Mechanical properties of Bouc-Wen spring

该模型工作原理的关系式为：

本次研究Bouc-Wen 模型具体参数取值如下：k为弹性刚度，用于模拟基础滑移前的静摩擦阶段，本次研究中均取极大值1×106kN/m［19］；r为屈服后刚度和弹性刚度之比，屈服后刚度用于模拟基础滑移阶段，取值为1×10-6；s为屈服指数，取值为2；α，β为滞后循环参数，︱α︱+︱β︱=1.0，分别取值α=0.5，β=0.5；Fy为屈服强度，其值等于砂石垫层滑动摩擦力，计算公式如下：

式中FN为静力分析中扩大基础的轴向压力。

考虑到扩大基础对地铁车站顶板的作用分布不均匀以及对桥墩集中力的扩散作用，同时为基础与地铁顶板间的内力传递提供足够支撑刚度，以扩大基础下局部地铁顶板单元划分为基础，如图10 所示，在每个扩大基础下均布16 个Bouc-Wen 弹簧，以使分析结果更接近实际情况。

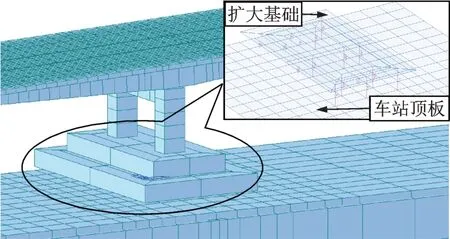
图10 Bouc-Wen 弹簧布置示意图Fig.10 Bouc-Wen spring layout diagram

3 地震动的选取与输入

3.1 地震波选取

目前工程中结构的抗震分析方法多采用反应谱法和时程分析法，时程分析法属于瞬态动力学分析方法，可以分析结构在地震荷载作用下的位移、应力随时间的变化情况。为了更深入研究结构在振动中体现的规律，本文采用时程分析法分析站桥组合体系的动力响应。

对于时程分析中地震波的选取，目前主要有实测地震波和人工地震波两种。实测波为各地实测典型地震的地震波，本次研究依据工程背景所在场地类型采用有完整记录的El Centro 实测波与1994 年美国Northridge 地震实测波，根据场地情况进行一定修正［20］后输入。

采用随机性方法基于设计反应谱可以合成人工地震波，其可以较为真实地模拟工程所在地的地震动作用。根据《中国地震动参数区划图》（GB 18306—2015）和相关工程背景，本次站桥组合体系所在地的场地类型为Ⅲ类场地，场地土由松散的中粗砂与密实、中密的细粉砂组成，加速度反应谱特征周期为0.4g，设防分类为乙类，设防烈度为8 度。人工地震波与反应谱的对比如图11 所示，三种地震波时程曲线如图12 所示。

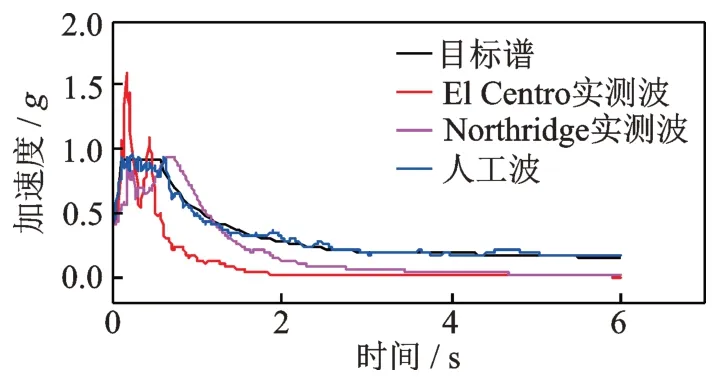
图11 地震波拟合谱Fig.11 Seismic wave fitting spectrum

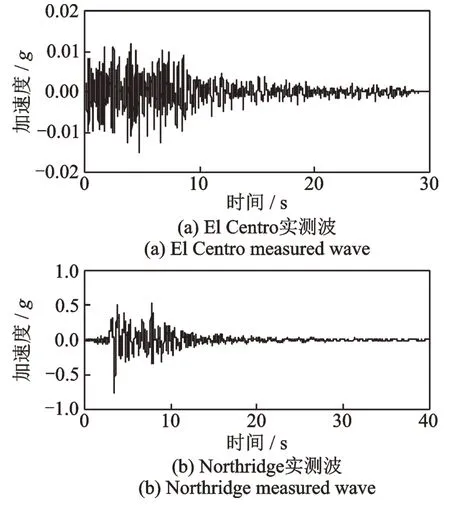
图12 地震波时程曲线Fig.12 Seismic wave time history curve

3.2 地震作用输入

经过综合考虑，将上述三种地震波作为地震动输入并对站桥组合体系进行时程分析。根据《城市桥梁抗震设计规范》（CJJ 166—2011）与《城市轨道交通结构抗震设计规范》（GB 50909—2014），按照8度罕遇抗震烈度进行设防，加速度峰值为0.4g，沿X方向输入地震动，如图13 所示。选取前两阶振型作为典型振型，采用瑞利阻尼假定进行非线性时程分析。

图13 地震波输入方向Fig.13 Seismic wave input direction

4 结构动力特性分析

采用多重Ritz 向量法分别对站桥合一结构与站桥分离结构进行特征值分析，以对比两种结构动力特性。其中，站桥分离结构中用于模拟扩大基础滑移的Bouc-Wen 模型弹簧等效刚度依据以往设计经验的最大基础滑移量偏保守估算。

图14，15 给出了两种结构形式典型的振型图。相比站桥合一结构，站桥分离结构的振型特征发生变化，同阶振型周期更长，动力特性更接近于上部桥梁结构与下部地铁车站结构各自独立运动，体现出明显的结构基础滑移特性。

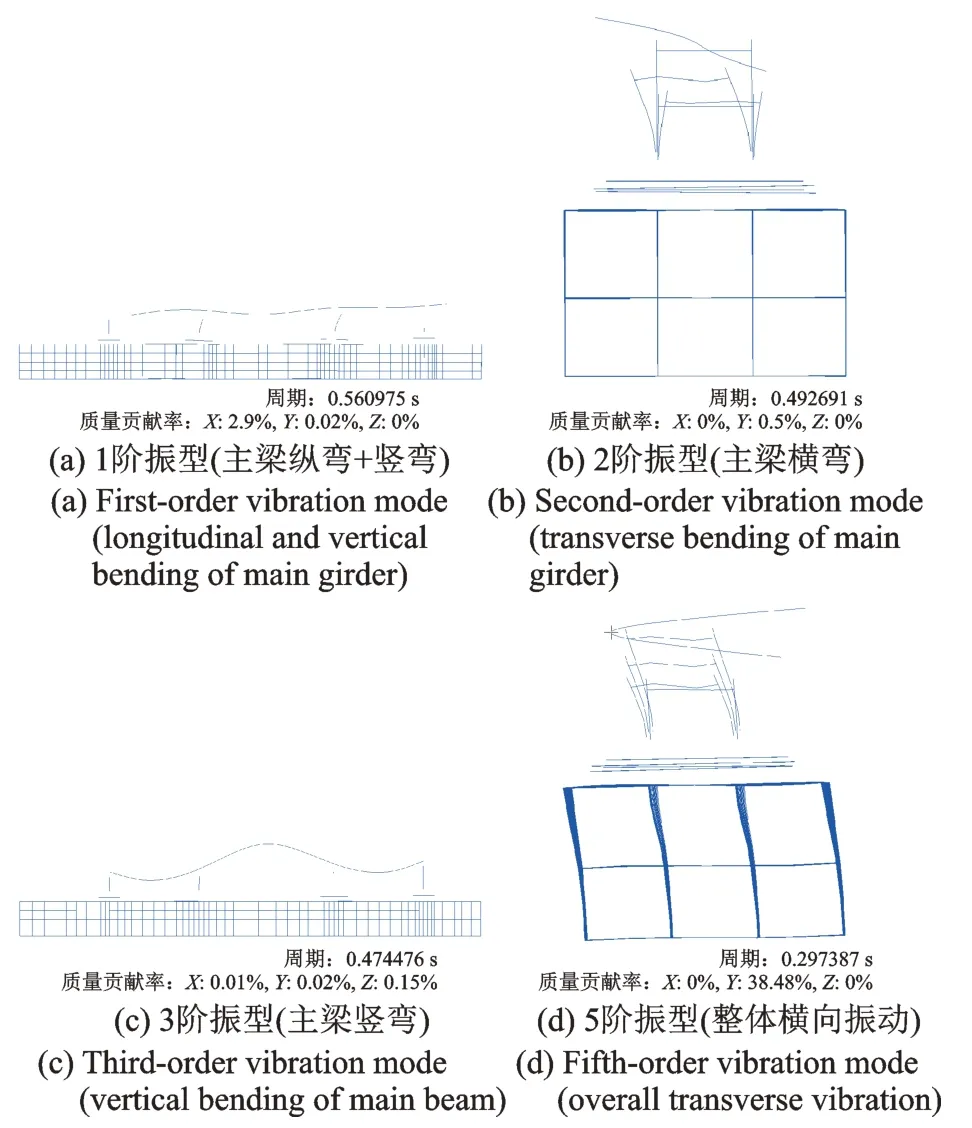
图14 站桥合一结构典型振型Fig.14 Typical vibration mode of station bridge integrated structure

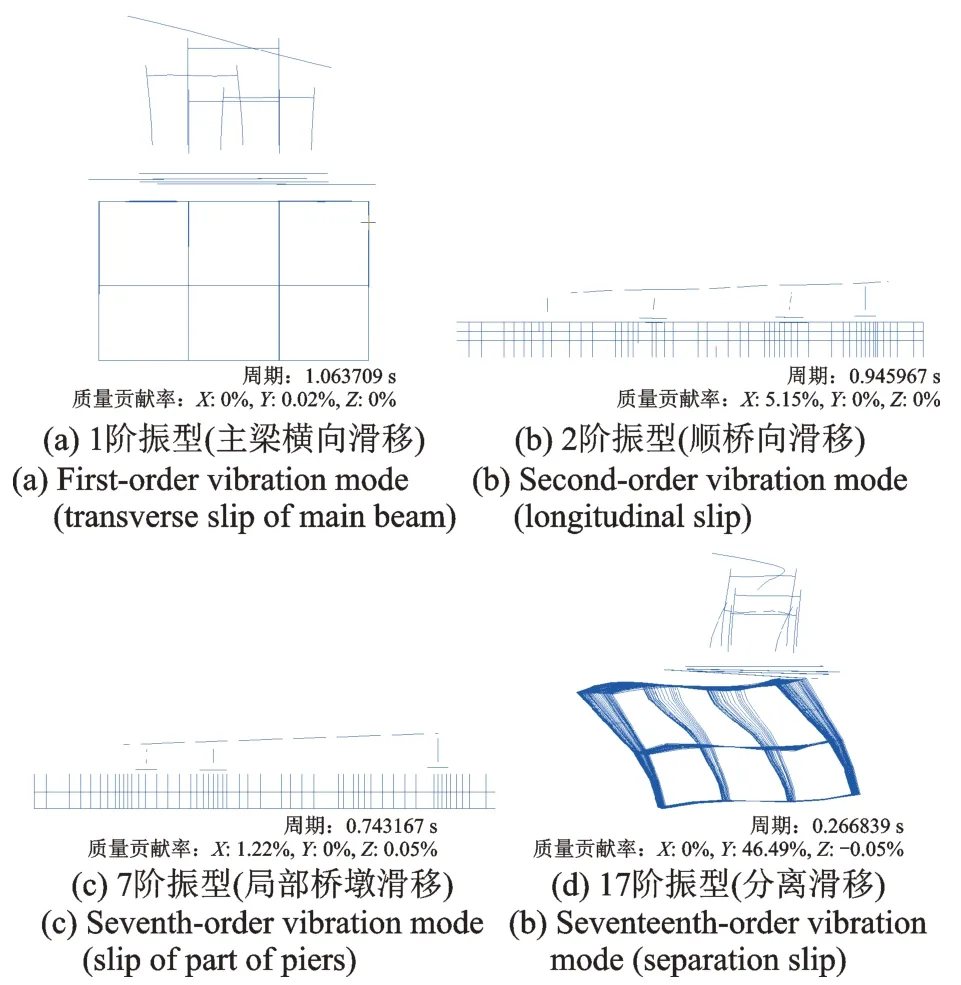
图15 站桥分离结构典型振型Fig.15 Typical vibration mode of station bridge separation structure

5 非线性时程计算结果

本次研究在考虑恒载（自重、二期荷载与土压力）的基础上对结构进行非线性时程反应分析，取输入的3 个地震波工况中的最大值进行比对，重点对不同站桥组合体系中地铁站与桥梁动力响应以及结构损伤进行系统比较，分析两种结构形式抗震性能的优劣。为便于叙述，将本次研究选取地铁站同侧桥墩与支撑柱沿顺桥向进行排序编号，其中地铁5，9，16，20 号支撑柱分别为1#～4#桥墩位置处对应支撑柱，如图16 所示。

图16 桥墩与地铁站支撑柱编号Fig.16 Numbering of pier and subway station support columns

5.1 地铁站动力响应对比

强震作用下地铁车站的动力响应是分析两种结构形式抗震性能差别的重要依据，如图17 所示为人工波工况下两种结构形式地铁站支撑柱柱顶与柱底的动力响应对比。整体而言，站桥组合体系中桥墩位置处对应的支撑柱明显承受了更大的弯矩和剪力，其中固定墩对应位置处的支撑柱动力响应较活动墩处更大，其余普通支撑柱的动力响应处于同一水平。

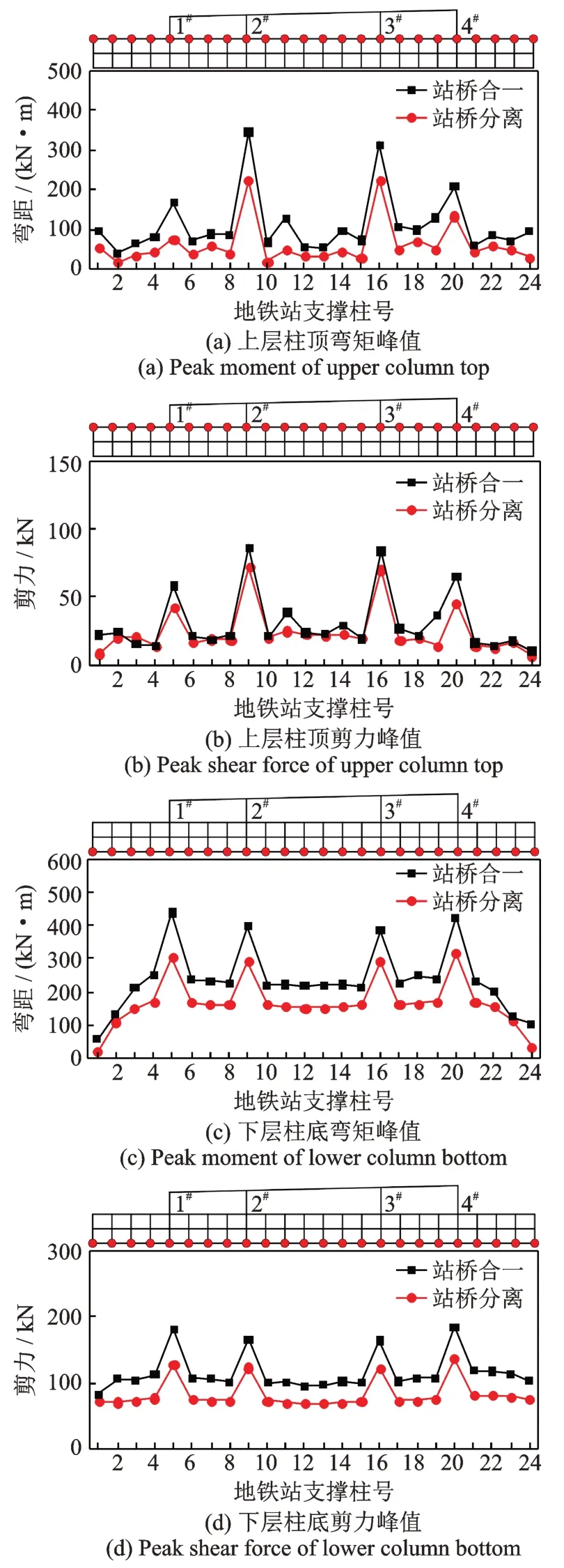
图17 地铁站支撑柱动力响应Fig.17 Dynamic response of supporting column in subway station

对于上层支撑柱，相比于站桥合一结构，站桥分离结构支撑柱的动力响应普遍减小，柱顶弯矩峰值的平均下降幅度为47.06%，剪力的平均下降幅度为18.73%。仅个别支撑柱柱顶剪力体现规律存在不明显差异，并未对总体规律产生影响。

对于下层支撑柱，站桥分离结构也起到了一定的减震作用，弯矩平均下降30.26%，剪力平均下降29.31%。但不同于上层支撑柱，地铁车站中板使得来自上层地铁车站的荷载更均匀地分配给下层支撑柱，桥墩位置处以及对应下层支撑柱动力响应水平大致相当，两侧下层支撑柱的弯矩和剪力较其他普通支撑柱呈明显下降趋势。

站桥分离结构中地铁车站结构动力响应整体小于站桥合一结构，产生这种现象是由于站桥分离结构仅靠桥墩扩大基础-砂石垫层-地铁站顶板间摩擦力传递水平力，遏制了地震过程中桥墩地震惯性力向地铁站的传递，较大程度上减小了地铁车站支撑柱的弯矩和剪力水平。换言之，级配砂石垫层在结构整体振动过程中起到了滑移隔震的作用，极大程度改善了地铁站结构整体抗震性能。

5.2 桥梁动力响应分析

5.2.1 桥墩动力响应分析

对于桥梁结构中桥墩的抗震研究，通常关心墩底的动力响应。如图18 所示为Northridge 地震波工况下桥墩墩底的弯矩与剪力绝对最大值。可以看出两种站桥组合体系中活动墩动力响应水平均小于固定墩，这是由于活动墩为边墩且与主梁间通过活动支座连接，在地震作用下承担的主梁横向和竖向惯性力均小于中间固定墩所致。

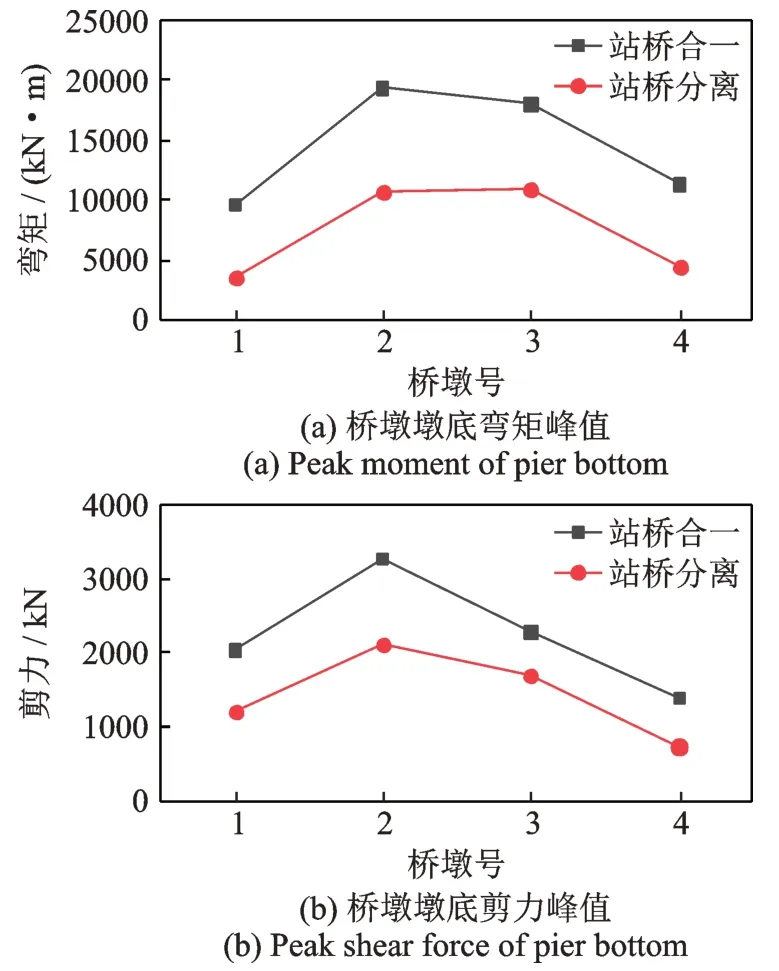
图18 桥墩墩底动力响应Fig.18 Dynamic response of pier bottom

相比于站桥合一结构，站桥分离结构对于桥墩墩底弯矩和剪力峰值均有一定程度的抑制作用。从动力响应最大的2 号固定墩来看，其弯矩峰值由站桥合一结构中的19304.6 kN·m 降低为站桥分离结构中的10715.1 kN·m，弯矩减震率达44.49%；剪力峰值则由3262.4 kN 降低为2115.8 kN，剪力减震率达35.15%。这说明级配砂石垫层减缓了地震过程中地铁车站结构与桥梁结构间动力响应的相互传递，在本文讨论范围内可适当提高桥梁抗震性能。

5.2.2 墩梁相对位移及基础滑移分析

桥梁抗震研究中，墩梁相对位移也是需要关注的问题。两种结构形式低墩侧顺桥向墩梁相对位移时程如图19 所示。

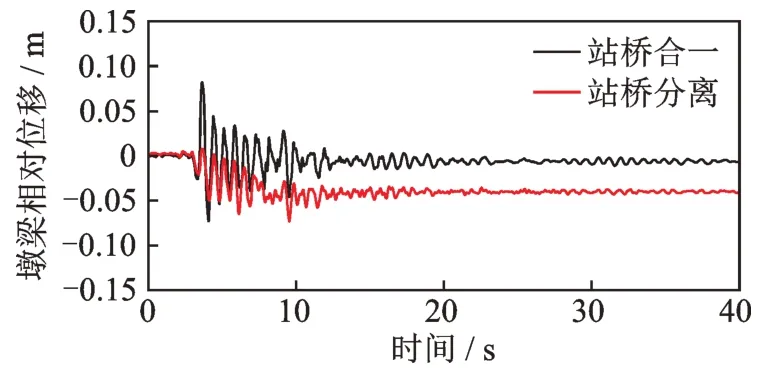
图19 低墩侧顺桥向墩梁相对位移时程图Fig.19 Time history diagram of relative displacement between beam and pier of low pier side along the bridge

可以看出两种结构形式的墩梁相对位移峰值差别不大，但站桥分离结构位移幅度更小，峰值出现时间更晚。同时时程分析表明，站桥分离结构出现了一定的残余位移，本次工程中盖梁纵向容许支撑宽度为1 m，符合《公路桥梁抗震设计规范》要求且远大于墩梁相对位移值，无落梁风险。

本次研究中连续钢箱梁桥在纵向地震动下的整体运动可视为刚体滑移振动，故1 号墩处墩梁相对位移可看做活动墩与固定墩墩顶相对位移。

图20，21 分别给出了3 号墩墩顶与墩底相对位移（下称桥墩变形）与桥梁基础相对地铁站顶板滑动位移（下称基础滑移）时程图。可以看出，站桥合一结构桥墩变形峰值为0.058 m，大于站桥分离结构，但基础没有发生滑移；站桥分离结构桥墩变形较小，而基础滑移量峰值达到了0.107 m，残余滑移位移量达到了0.037 m，远大于站桥合一结构。这说明两种站桥组合体系产生墩梁相对位移的原理不同，站桥合一结构产生墩梁相对位移主要原因为桥墩变形，而站桥分离结构的墩梁相对位移由桥梁基础滑移和桥墩变形叠加而形成，二者在地震中的变形如图22，23 所示。站桥分离结构桥墩变形更小，桥梁结构在地震过程中更趋于整体平动，更不易发生损伤。

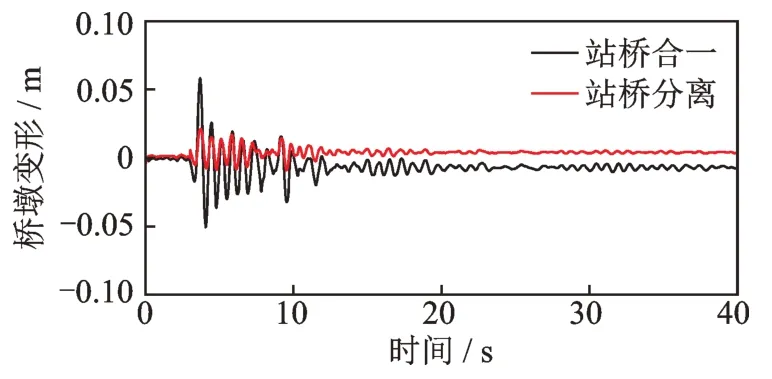
图20 3 号墩变形时程图Fig.20 Deformation time history of 3# pier

图21 3 号墩基础滑移时程图Fig.21 Time history diagram of 3# pier foundation slip

图22 站桥合一结构桥墩变形Fig.22 Deformation of pier of station-bridge integrated structure

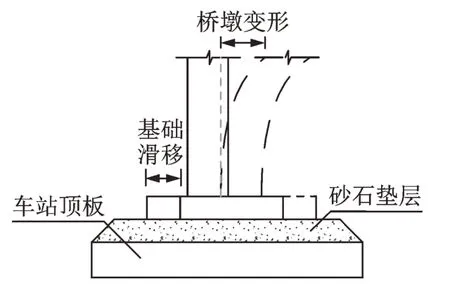
图23 站桥分离结构桥墩变形Fig.23 Deformation of pier of station-bridge separation structure

同时可以发现，站桥分离结构墩梁相对位移向某一特定方向发展，并产生一定残余墩梁相对位移，出现这一现象的原因是固定墩与活动墩在振动过程中滑移量不同，如图24 所示。

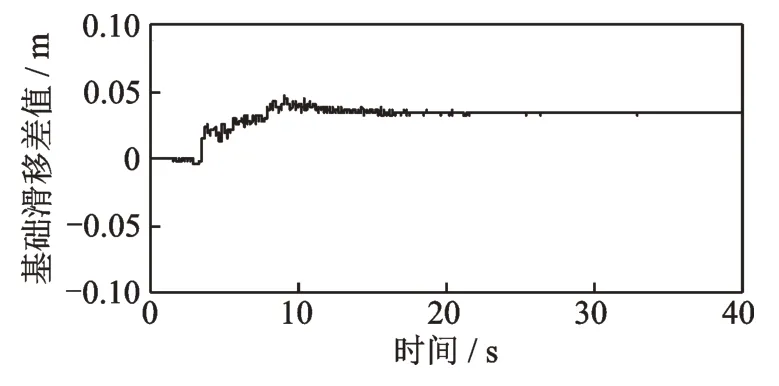
图24 站桥分离结构1，3 号墩基础滑移量差异值Fig.24 Foundation slip difference of 1# and 3# piers of station-bridge separation structure

在地震过程中，活动墩承担了半跨主梁重量，由于采用了滑动支座，在滑动后，仅传递摩擦力给下部结构，而固定墩在承担一跨主梁重量的同时，在地震作用下将承担的所有主梁惯性地震力给下部结构。因而，二者在地震过程中两种桥墩扩大基础和垫层间的摩擦力和承受地震力存在差异，固定墩基础更易滑移，产生残余位移。

5.3 桥墩损伤分析

为了深入研究不同站桥组合体系在地震过程中的损伤发展，本文依据DM（Damage Measure）准则对桥墩结构在地震作用下的塑性行为进行分析。DM 准则为定义结构极限状态的通用准则，该准则定义DM为结构在不同地震强度下的损伤指标度量值，将DM的阈值CDM定义为结构倒塌的极限值点，当DM≥CDM时，结构发生倒塌。

美国FEMA356 规范基于DM 准则，根据层间位移角θmax定义了结构三个极限状态点：立即使用（Immediate Occupancy，IO）、生命安 全（Life Safe，LS）和防止倒塌（Collapse Prevention，CP）［21］，其中IO 极限状态为塑性点，CP 极限状态为倒塌点。MIDAS/Civil 软件据此将结构塑性铰状态分为5 个等级，如表5 所示。

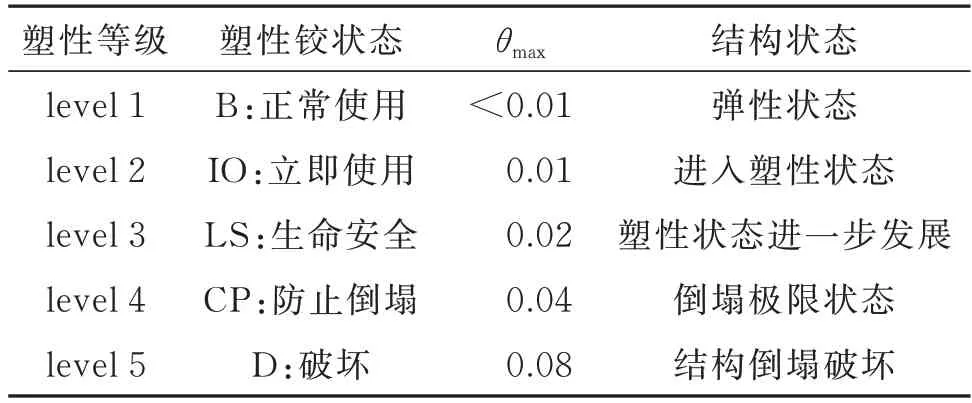
表5 塑性铰状态等级Tab.5 Plastic hinge state grade

在El Centro 地震波工况下，对比不同站桥组合体系中各桥墩最终塑性状态及形成时间，如图25所示。

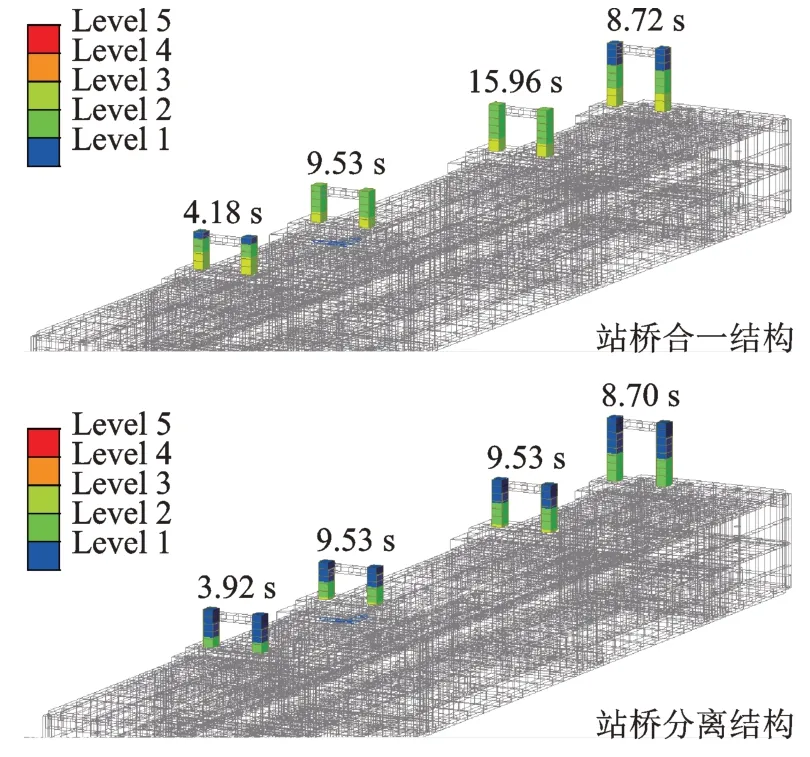
图25 两种结构最终塑性状态及形成时间Fig.25 Final plastic state and formation time of two structures

整体而言，站桥组合体系中桥墩墩底部分会更先发展至更高等级的塑性状态，产生相应的损伤。对比两种结构形式的最终塑性状态，站桥分离结构各墩顶均处于弹性状态，活动墩墩底为立即使用状态，仅固定墩墩底发展到生命安全状态。而站桥合一结构仅活动墩墩顶处于弹性状态，所有桥墩墩底均发展至维持生命安全状态。站桥分离结构的桥墩达到塑性状态等级更低，达到高等级塑性状态的结构范围更小，最终损伤程度更轻微，体现出更为优良的抗震性能。

以3 号墩为例，其滞回耗能曲线如图26 所示。可以看出在地震过程中，站桥合一结构桥墩明显进入更高等级塑性状态，而站桥分离结构桥墩基本处于弹性阶段，损伤程度更轻。

图26 3 号墩滞回耗能曲线Fig.26 Hysteretic energy consumption curve of 3# pier

两种结构形式中桥墩首次达到立即使用状态（level 2），即进入塑性状态的时间也能体现二者抗震性能的差异，如图27，28 所示，在0.11 s 与0.35 s时，站桥合一结构的固定墩大部分和1 号墩墩底分别进入塑性阶段，而直到1.69 s 和4.80 s 时，站桥分离结构1 号墩和3 号墩墩底才分别进入塑性阶段。

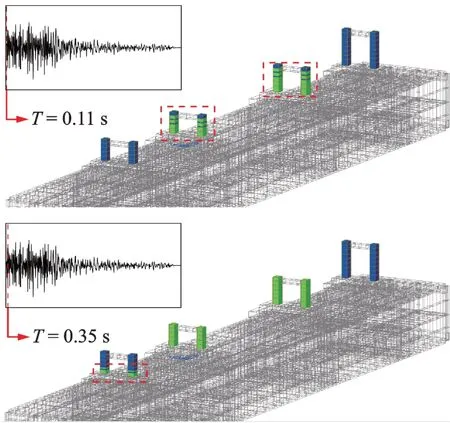
图27 站桥合一结构出现塑性状态时间Fig.27 Plastic state time of station-bridge integrated structure

图28 站桥分离结构出现塑性状态时间Fig.28 Plastic state time of station-bridge separation structure

站桥分离结构中桥墩出现塑性状态的时间更晚，对结构损伤有一定延缓作用。站桥合一结构中较活动墩更早进入塑性阶段的固定墩在站桥分离结构中更晚进入塑性阶段，说明站桥分离结构对固定墩损伤的延缓作用更明显，对整体结构起到了隔震保护作用。

6 结论

本文依托某实际地铁车站桥梁结构，使用有限元分析软件MIDAS/Civil 建立了站桥合一结构与站桥分离结构的三维非线性动力有限元模型并进行分析，对比两种结构形式在地震过程中动力响应以及损伤机理的差异，所得结论如下：

（1）从地铁车站动力响应来看，两种站桥组合体系中桥墩位置对应的地铁站立柱的动力响应水平明显大于普通立柱。而站桥分离结构可大幅降低地铁站支撑柱弯矩和剪力水平，极大程度改善了地铁站结构整体抗震性能。

（2）从桥梁动力响应来看，两种站桥组合体系固定墩动力响应更大。站桥分离结构中桥梁结构动力响应水平低于站桥合一结构，且桥梁整体趋于整体平动，砂石垫层起到良好的隔震作用。但站桥分离结构不同桥墩基础滑移量存在差异，导致产生墩梁残余相对位移。

（3）从桥墩损伤来看，站桥组合体系中桥墩损伤会先出现在墩底位置。站桥分离结构桥墩损伤程度更轻，出现塑性状态的时间更晚，对结构损伤有一定延缓，起到了隔震保护作用，体现出更优良的抗震性能。

（4）在站桥组合体系实际工程设计中，应结合工程现场实际情况，优先选择站桥分离结构，设计时需注意对桥墩位置对应处地铁站支撑柱的内力控制，同时应注意对墩梁相对位移及基础滑移的限位。