基于广义简约梯度算法的落差指数法参数优选

周绍阳,王 悦,龚朝海

(长江水利委员会水文局 长江下游水文水资源勘测局,江苏 南京 210011)

0 引 言

在水文测验领域,相比水位观测,流量测验更为复杂且费时费力。水位和流量在客观上存在显著关联性,可通过实时监测水位推算断面相应流量。然而,在天然河道中,受洪水涨落、断面冲淤、变动回水等因素影响,水位流量关系通常不具有单值函数的特性,呈不稳定形态,无法直接通过水位推算相应流量,只能采用连时序等方法整编流量;而连时序法需要布置大量测次,工作量大。因此,为了减少流量测次,降低工作强度,有必要建立水位与流量的单值化关系[1-2]。

水位和流量单值化关系研究的主要方法包括校正因素法、抵偿河长法、落差法等[3]。落差指数法是以落差法为基础,通过优选落差指数β,建立水位与流量同落差的β次方之比例关系。该方法适用于断面基本稳定、受变动回水或变动回水及洪水涨落综合影响的测站。自20世纪70年代以来,该方法逐步发展完善,已被广泛应用于水文站的资料整编[4]。在实际应用中,落差指数和落差系数等参数的确定是影响落差指数法精度的主要原因之一[5]。

传统参数确定方法通常是利用相关资料,通过试错法或优选法确定部分参数,再通过点绘关系图或试错法求解其他参数。该方法存在以下不足之处:① 点绘关系图工作量大,且受人工经验和技能水平影响,存在非唯一解的问题;② 各参数之间可能存在密切关联,传统方法得到的参数不一定是最优结果。近年来,随着计算机技术和机器学习的快速发展,落差指数法的参数优选问题得到更广泛研究。李正最[6]提出了一种直接求解落差指数法参数的方法,该方法简单易行,但计算量较大。喻娓厚等[7]则利用遗传算法的全局寻优能力对落差指数法中的参数进行优化,该方法适用范围广,但实现较为困难,需要对遗传算法有一定的理解。邓才等[8]引入粒子群算法直接求解落差指数法中的参数,该方法计算速度快,但算法实现较为困难,参数设置不当可能会导致出现局部最优解的情况。

本文研究了落差指数法原理,发现落差指数法的参数优选可视为一个非线性约束优化问题。广义简约梯度算法是求解非线性约束问题的最有效方法之一。相比其他优化算法,该方法具有简单实用、算法收敛快、计算精度高等优点[9-10]。因此,本研究采用广义简约梯度算法对落差指数法中的参数进行优选,以确定水位与流量的单值化关系。

1 研究方法

1.1 落差指数法

1972年,研究发现落差指数在0.5上下变动可明显提高定线精度[3]。1972～1975年,在深入研究了落差指数和相应的落差水尺优选及误差分析的基础上,提出了落差指数法[4]。落差指数法可由曼宁公式导出[11]:

(1)

式中:q为单值化流量,m3/s;Q为实测流量,m3/s;β为综合落差指数;ΔZ为综合落差,m,由式 (2) 计算:

ΔZ=α1ΔZ1+α2ΔZ2+…+αnΔZn

(2)

式中:ΔZ1,ΔZ2,…,ΔZn为与各参证站的同时落差,m;α1,α2,…,αn为落差系数,且α1+α2+…+αn=1。

单值化流量与水位具有明确的函数关系,在实际水文整编工作中,常采用的函数关系主要有指数方程、对数方程和多项式方程[12],其中,多项式方程表达式为

q=k0+k1Z+k2Z2+…+kmZm

(3)

式中:k0,k1,k2,…,km为多项式系数;Z为测站水位,m。

由式 (1)～ (3) 可知,整个求解过程中需要确定β,α1,α2,…,αn,k0,k1,k2,…,km等参数。利用传统方法很难将所有参数一起优化,一般先初定β值,再通过试错法定出Z-q关系曲线,直至定线精度符合单一曲线的定线要求。而利用广义简约梯度算法可快速实现参数的全部优化。

1.2 广义简约梯度算法

简约梯度算法(Reduced Gradient Method,简称RG算法)是非线性规划的单纯形法应用于仅具有线性约束的非线性约束规划问题。后来,RG算法被推广到非线性约束问题,得到广义简约梯度算法(Generalized Reduced Gradient Method,简称GRG算法)[13]。GRG算法是一种针对含有非线性约束的优化问题的求解方法[14-15],优化问题可简化为

minF(X)X∈En

s.t.H(X)=0

(4)

L≤X≤UL,U∈En

式中:X为设计变量;F(X)为目标函数;En表示n维空间;H(X)为约束函数,H(X)=[h1(X),h2(X),…,hm(X)]T;L为设计变量X的下限向量,L=[l1,l2,…,ln]T;U为设计变量X的上限向量,U=[u1,u2,…,un]T。

求解时,首先将X分为两部分,即X=[XB,XN]T。其中,XB为基向量,m维;XN为非基向量,(n-m)维。相应地,L=[LB,LN]T,U=[UB,UN]T。由隐函数存在定理可知,存在连续映射:

XB=V(XN)

(5)

式中:V(XN)为连续映射函数,将XN的取值通过某种关系映射到XB的取值。

目标函数F(X)可转化为

F(X)=F(XB,XN)=f(XN)

(6)

式中:f(XN)为关于非基向量XN的目标函数。

原来n个变量的目标函数F(X)可以转化为n-m个变量的函数f(XN),则f(XN)在Xk关于XN的梯度即为简约梯度,可得到F(X)关于XN的简约梯度为

∇f(XNk)=∇NF(Xk)-∇NH(Xk)

[∇BH(Xk)]-1∇BF(Xk)

(7)

式中:∇f(XNk)为简约梯度,表示非基向量XN的目标函数关于XN在第k步迭代中的梯度;∇NF(Xk)为原始目标函数关于非基向量XN在当前步骤k的梯度;∇NH(Xk)为原始约束函数关于非基向量XN在当前步骤k的梯度;∇BH(Xk)为原始约束函数关于基向量XB在当前步骤k的梯度;∇BF(Xk)为原始目标函数关于基向量XB在当前步骤k的梯度。可简记为

∇f(XNk)=[r1,r2,…,rn-m]T

(8)

式中:r1,r2,…,rn-m表示简约梯度向量∇f(XNk)的分量。

定义Sk=[s1,s2,…,sn-m]T,其中:

(9)

令

(10)

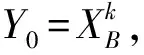
Yc+1=Yc-H(Yc,XNk+1)[∇BH(Y0,XNk+1)]-1

c=1,2,…

(11)

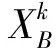
最后,求得满足H(Yc+1,XNk+1)=0时的Yc+1,即可得到最优值。

2 应用案例

2.1 研究区域概况

大通水文站位于安徽省池州市贵池区梅龙街道,东经117°37′,北纬30°46′,是国家一类水文站,也是长江下游干流最后一个径流控制站。测验河段上下游10 km范围内基本顺直。上游有皖河、秋浦河等水汇入,下游有九华河、青弋江等汇入,均对断面水流影响较小。影响水流的主要因素为上游干流来水和上游219 km处鄱阳湖出水。由于大通水文站位于潮区界点,距海口624 km,枯季感潮显著。多年来,该站水位流量关系虽然复杂,但总体稳定。落差指数法在大通水文站资料整编中具有较好的适用性,单值化后的水位流量关系采用多项式函数效果更优[12]。安庆水位站作为大通水文站上游参证站,位于安徽省安庆市沿江东路,距大通水文站约80 km。测站区位见图1。

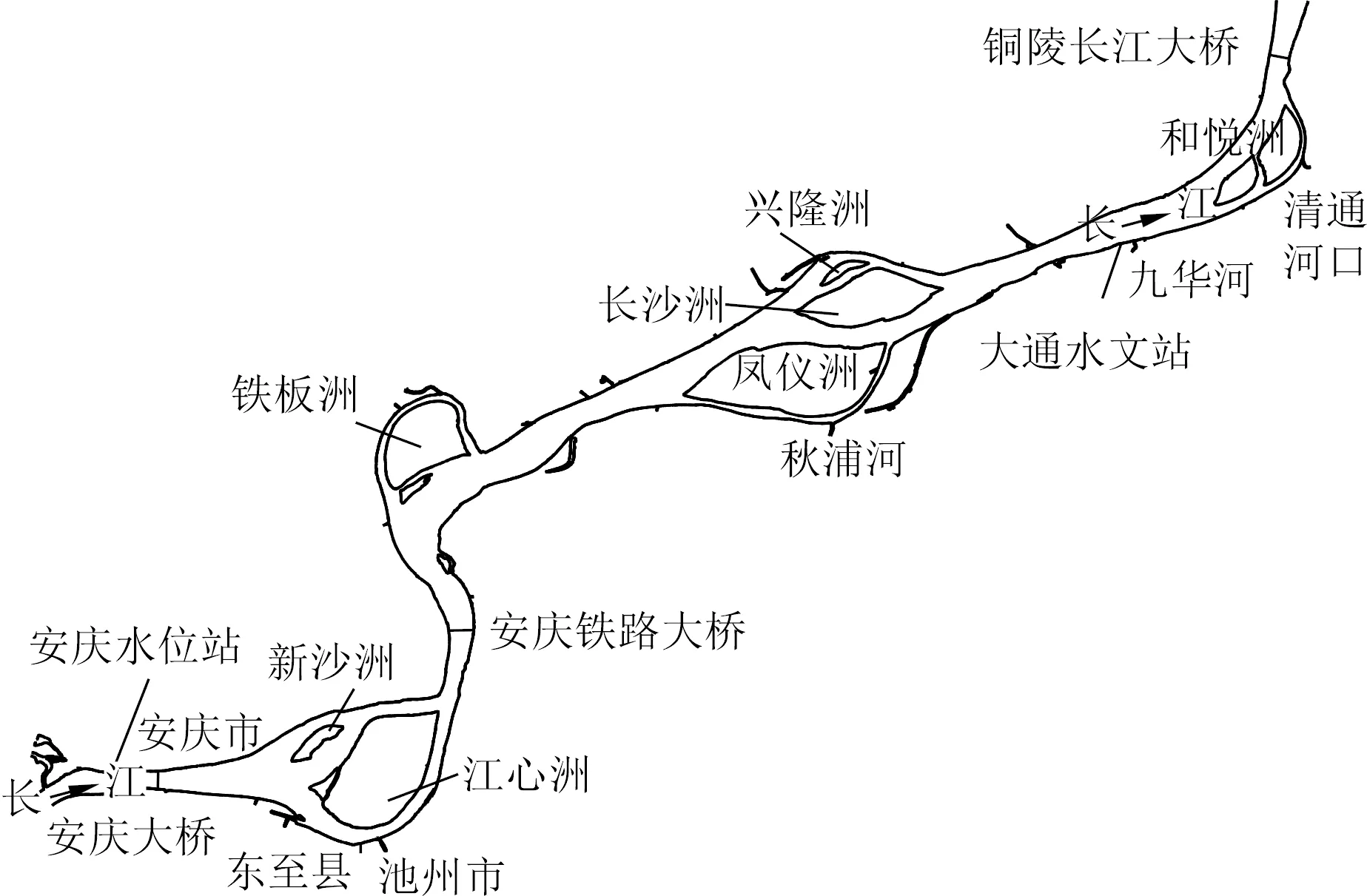
图1 大通水文站区位Fig.1 Location of Datong Hydrological Station

2.2 数学建模

采用落差指数法进行参数优选,主要精度评价指标为实测点对关系线的随机不确定度,计算公式为

(12)

(13)

结合大通水文站特性,公式 (2),(3),(1) 和(4) 可对应改写为下式 (14),(15),(16) 和(17)。

ΔZ=Z安庆-Z大通

(14)

q=k0+k1Z大通+k2Z大通2+k3Z大通3

(15)

Qci=q(ΔZ)β

=(k0+k1Z大通+k2Z大通2+k3Z大通3)·

(Z安庆-Z大通)β

(16)

(17)

式中:ΔZ为安庆与大通的落差水位,m;Z安庆为安庆站水位,m;Z大通为大通站水位,m;q为大通站单值化流量,m3/s;k0,k1,k2,k3为多项式系数。

2.3 算法实现

算法编程可以通过FrontlineSolvers、Matlab等商用软件实现[16]。考虑到大通水文站每年的实测数据只有40组左右,采用Excel规划求解工具中GRG算法模块实现参数优选更加便捷,算法实现流程见图2。节选大通水文站2018～2022年整编数据并代入数学模型计算,参数优选结果见表1。

表1 参数优选结果

图2 算法实现流程Fig.2 Flow chart of implementation of algorithm

3 结果分析

3.1 成果检验

将表1中计算出的相关参数代入公式 (15),即求得2008～2022年大通水文站水位流量关系单值化曲线,见图3。由图3可知,关系曲线拟合良好,符号、适线、偏离数值检验合理。统计实测点流量与推算流量的系统误差及随机不确定度,统计结果见表2。系统误差范围为-0.13%～-0.02%,随机不确定度范围为2.84%～5.24%。根据SL/T 247-2020《水文资料整编规范》中水位流量关系定线精度指标要求,采用水力因素法的一类精度的水文站,应满足系统误差不超过±2%,随机不确定度不大于10%。由此可见,基于GRG算法的定线精度满足规范要求,且在典型年(2020年长江流域特大洪水,2022年长江流域极端干旱)的情况下,成果可靠。

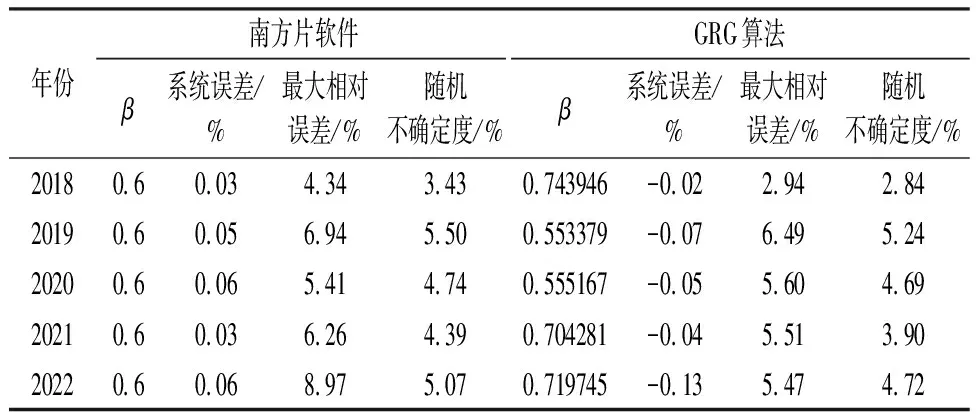
表2 GRG算法与南方片软件定线精度对比

3.2 精度对比

大通水文站现有落差指数法是基于南方片软件实现的,经验落差指数则是根据1998～2012年共15 a的实测资料试算求得,β=0.6,且在2013～2022年流量资料整编中验证了可靠性。表2为2018～2022年南方片软件定线与GRG算法定线的精度统计。由表2可知,两种方法均可满足大通水文站定线要求,系统误差无明显区别,但GRG算法定线的随机不确定度和最大相对误差(除2020年)均小于南方片软件定线。总体而言,基于GRG算法的定线精度更高。

4 结 论

(1) GRG算法计算速度快且易于实现,是目前求解约束非线性最优化问题有效的方法之一。本文将该方法应用于大通水文站2018～2022年落差指数法参数优选,并与传统方法进行了对比。结果表明:基于GRG算法的落差指数法参数优选是可行且实用的,不仅实现了参数的全部优化,提高了定线精度,还简化了传统方法的工作步骤,且不需要人工干预,为落差指数法的参数求解提供了一种新思路。

(2) 使用GRG算法的前提是落差指数法适用于测站。当测站水流或断面条件发生变化时,应注意分析方法的适用性。比如,大通水文站2022年个别数据不满足定线精度要求,其主要原因为该站受极端枯水及感潮等因素影响,水流受下游水位顶托影响严重,导致测站不符合落差指数法的适用条件,南方片软件和GRG算法的定线误差均较大。因此,遇到反常数据时应结合测站特性及水情加以分析。