基于全局与滑动窗口结合的Attention机制的非侵入式负荷分解算法

董哲,陈玉梁,薛同来,邵若琦

(北方工业大学,北京 100043)

0 引 言

有专家学者提出非侵入式负荷监测[1-2],目的是将整体能耗分解为单个设备的能耗。由此可以通过帮助家庭了解具体单个设备的能耗情况,从而合理规划家庭的整体能源使用[3-6],文献[7]研究表明,分类信息可以帮助家庭减少多达5%～15%的能源消耗。除此以外,非侵入式负荷分解是配电网需求侧精细化管理的关键技术,同时也是人工智能技术在配电领域的重要应用方向之一。相较于传统的侵入式负荷分解,利用信号处理或人工智能等方法的非侵入式负荷分解成本更加低廉,也更加安全可靠。

NILM是从一个监测的整体能耗中提取单个能耗信息,这属于单通道盲源分离(a single-channel blind source separation,BSS)问题。通常人们可以从用电总负荷数据中识别出包含哪种具有丰富特征的用电设备,例如,冰箱的工作状态(见图1),但在分解过程中,还存在着一些不确定因素的干扰,包括采集功率数据中的噪声,或多种相似工作状态,以及多个设备同时开启或同时关闭的情况,所以仅凭经验来对负荷进行分解是很不可靠的。

图1 冰箱的工作状态

文献[8-10]提出了加性阶乘隐式马尔可夫模型(AFHMM)是可以构造NILM模型的自然方法,在此基础上使用推理算法来预测设备信号,但效果并不理想。为了解决可识别性问题,文献[11]提出加入数据的本地信息(例如,设备功率水平,开关状态变化和持续时间),文献[12]在模型中纳入了全局信息(例如循环总数和总能耗)。但是,这些方法所需的标注需要手动提取,这使得这些方法难以应用。因此,使用深度学习在训练过程中自动提取这些特征信息更为有效。

文献[13]将深度学习方法应用于NILM,文章中提出了三种深度学习方案,分别是卷积神经网络(CNN),长短期记忆网络(LSTM)和堆叠式降噪自动编码器,并在UK-DALE[14]数据集上验证了深度学习方法应用在NILM的。文献[15]在提取单个负荷激活特征时,采用了具有两层的双向长短期记忆(LSTM)单元的递归神经网络架构,并在数据集(REDD)上测试了其模型[16]。这些方法学习具有相同时间戳的总负荷功率和单个负荷功率之间的非线性回归,但是这些方法存在着分解功率滞后,变化速度较慢,没有对于真实功率保持良好的跟踪性的问题。

为此,本文采用深度学习框架,提出一种基于全局与滑动窗口结合的Attention机制的负荷分解的方法,利用文献[17]发布的 REFIT数据集进行模型的训练与测试,并与文献[13]提出的基于CNN 和长短时记忆模型 (Long Short Term Memory,LSTM)的模型进行对比,验证本文所提模型的优越性。

1 非侵入式负荷分解模型

模型由6个部分组成,分别是输入层、功率嵌入层、双向LSTM组成的编码层、Attention层、单向LSTM的解码层、和输出层(见图2)。并加入Dropout等方法以解决可能出现的过拟合问题。

图2 系统结构框图

1.1 功率嵌入

低频数据集采样的总用电功率数据可能记录了几个月甚至几年的时间,而一整天的采样点就成千上万条,模型的输入长度是有限的且固定,所以对数据进行分段是必不可少的。对于m种用电负荷设定其输入深度学习模型的长度分别为N1,N2…Nm。

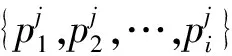
(1)

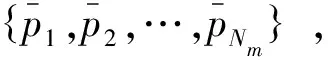
相较于自然语言处理中的词嵌入,通过捕捉不同的语言信息或依靠语法语义以及相似度的方法来构造词嵌入矩阵,本文采用均匀分布的初始化矩阵作为功率嵌入矩阵E=[v_s×e_s],v_s的大小取决于可能出现的总功率最大值,若取值不够大则可能会导致某些功率值没有对应映射向量的情况。e_s为单类功率值经由功率嵌入矩阵映射后的序列长度。

(2)

从功率序列到功率矩阵的映射保证了功率与高维向量的对应关系,有利于编码器抽取功率序列的时序信息,且可以有效降低深度学习模型的运算量以及提高分解功率的准确性。

1.2 基于Attention的Seq2seq模型

序列到序列(sequence to sequence,Seq2seq)是一种编码-解码(encoder-decoder)结构的模型,模型结构如图3所示,其中,Encoder部分是将输入的序列压缩成指定长度的向量,称其为向量C,Decoder部分负责将向量C解码成输出序列。

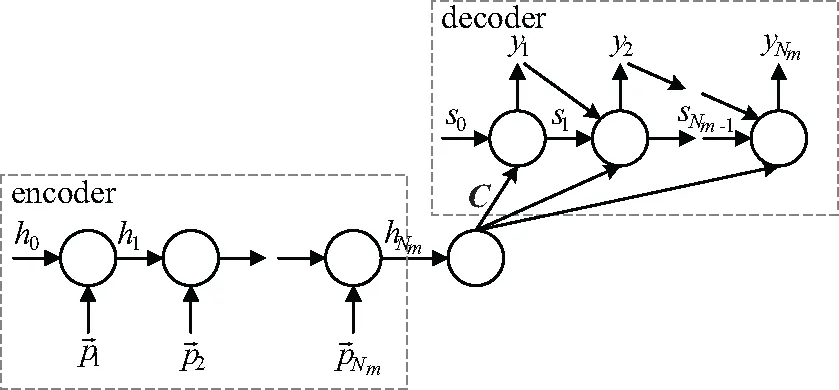
图3 Seq2seq模型

但随着输入序列长度的增加,编码器难以将所有输入信息编码为单一向量,编码信息缺失,难以完成高质量的解码。Bahdanau attention是一种加性Attention机制,如图4所示,将Decoder的隐藏状态和Encoder所有位置输出通过线性组合对齐,并计算相关权重得到向量C,进而保证用于解码的信息的完整性。

(3)

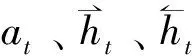
将每一时刻的ai与前一时刻解码层的隐藏状态st-1拼接,然后将其输入到全连接层并采用Softmax激活函数得到对于当前时刻的权重,计算公式如下:

et,i=Softmax(tanh(st-1Wdecoder+XWencoder)Wdense)

(4)

(5)

在解码过程中,在时间步t时,将语义向量C、前一时刻的隐藏状态st-1和输出yt-1作为输入,计算公式如下:

st=f(C,st-1,yt-1),t=1,2,…,Nm

(6)

再得到从d1到dNm的分解功率概率分布序列:

dt=g(st),t=1,2,…,Nm

(7)

式中g为从隐藏状态st到dt=[v_s*1]的分解功率概率密度分布的映射函数。由功率嵌入可得,v_s代表可能出现的总功率大值,那么dt即为分解功率在各个整数功率值的概率密度分布,选取其中概率大的功率值作为t时刻分解功率输出yt。

yt=ArgMax(dt)

(8)

1.3 全局与滑动窗口相结合的Attention机制

Attention的计算方法时间和空间复杂度都是O(n2),这使得难以在长序列上进行训练。比如洗衣机,洗碗机等电器负荷激活时间一般较长,在训练模型的时候会有较大的计算量。因此本文采用全局注意力机制结合滑动窗口注意力机制(GSWA,global+sliding window attention)的方法来降低模型的运算量。

1.3.1 滑动窗口注意力机制

局部注意力机制(local attention)是一种介于soft attention和hard attention之间的一种attention方式,可以将注意力定位在关键数据附近,进而减少attention机制的运算量。local attention首先会为decoder端当前的词,预测一个Encoder端对齐位置(aligned position)pt,然后基于pt选择一个窗口,用于计算向量C。其中位置向量pt预测的准确率直接影响到最终结果。然而在功率预测模型中,输入和输出是在相同时间戳下的总负荷功率和单负荷功率,其中位置向量pt就是当前t时刻的位置,故采用滑动窗口注意力机制(SWA,sliding window attention)可以在保证结果准确率的情况下提升attention 机制的运算效率。选择滑动窗口的范围(见图5)。

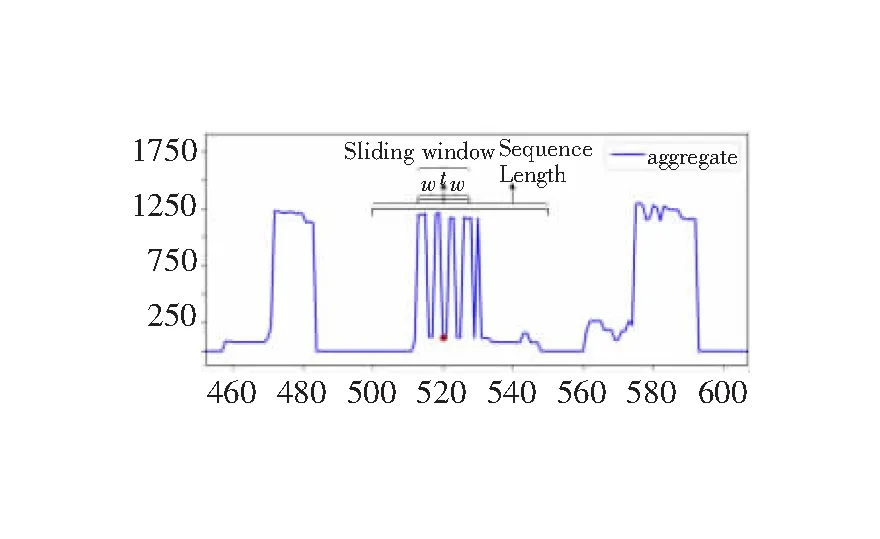
图5 滑动窗口的选取

计算公式如下:

(9)

1.3.2 空洞滑动窗口注意力机制

为了进一步增加提取特征的范围而不增加计算量,可以将滑动窗口“扩大”。本文在滑动窗口上加入空洞以此来增加提取功率变化特征的范围,即空洞滑动窗口注意力机制(DSWA,dilated sliding window attention),类似于空洞卷积神经网络(dilated/atrous convolution)[18-20],是在标准的卷积层(convolution map)里注入空洞,以此来增加感受野(reception field)。相比原来的正常卷积层,dilated convolution 多了一个超参数,称之为空洞率,指的是卷积核之间的间隔数量。本文在滑动窗口上加入扩张大小为d=1的间隙,窗口范围选择计算公式如下:

(10)

式中在范围内每个点相隔d个点,则每一层注意力区域约为d×w,即使d的值很小,也可以让提取信息的区域成倍增加。

1.3.3 全局与滑动窗口结合的注意力机制

DSWA相较于SWA虽然扩大了信息提取的区域,但不够灵活,空洞的加入也可能会漏掉功率变化的特征信息。因此,本文提出全局注意力机制与滑动窗口注意力机制相结合的方法,对功率输入序列进行处理,在功率值变化较大的地方加上标签,标签处采用全局注意力机制(global Attention)用于更好的关注功率序列的整体信息。其中标签的数量与电器的工作状态有关,而与输入序列的长度无关,故全局和滑动窗口组合的注意力机制在计算复杂度上仍为O(Nm)。

2 损失函数

由于本文模型将分解功率的值回归问题转换为了求取功率分解值在各个离散整数功率值下概率的多分类问题,故采用多分类交叉熵作为模型的损失函数,其定义如下:

(11)

式中Nm是单个用电负荷序列长度;v_s代表总负荷功率可能出现的类数;yt,i为t时刻真实功率为j的概率,该概率仅在j与t时刻真实功率相等时为 1,其余时刻为 0;ft,i(x) 为t时刻模型输出分解功率为j的概率。

3 实验结果与分析

3.1 数据集的选取

本文选取了文献[17]于2015 年发布的REFIT (Cleaned)数据集进行模型的训练与测试,其中包含20户家庭的单个负荷有功功率及家庭总负荷有功功率信息,有功功率的采样间隔为8 s。数据集的采集时间跨度从2013年持续到2015年,并对其中的数据进行了清洗:对于重复的时间戳进行合并,单个设备出现超过4 000 W的功率置零,对于缺失的数据进行填充。

3.2 用电器的选取

本文选取冰箱、热水壶、微波炉、洗衣机及洗碗机这5种常见用电器作为研究对象(见表1)。这5种用电器具有不同的工作状态,其中冰箱是周期性运行用电器,热水壶是大功率用电器,微波炉运行时间短且功率变化频率高,洗衣机和洗碗机是的长时间多状态用电器,可以全面验证本文所提模型的负荷分解性能。

表1 电器数据选择

3.3 提取负荷激活特征

根据每种用电电器的实际工作状态,从数据集中提取它们在运行时的功率数据,称为提取负荷激活特征,负荷激活特征参数与数量如表2所示。

表2 负荷激活特征提取的参数

3.4 构造均衡数据集

在提取负荷激活特征后,构造训练数据集。在本文模型中,每种负荷模型的输入为固定长度的序列,其输入的序列长度如表2所示。对于5种用电器,分别按照下列步骤构造其对应训练数据:

1)根据该用电器模型的输入序列长度Nm创建两个全零序列,一个用作存储输入的总用电功率,一个用作存储模型输出的单负荷功率;

2)在50%概率下,从该用电器的负荷激活特征中随机选取,即某次运行阶段的功率消耗数据,并在保证该段负荷激活可以完全放入序列的前提下,随机选取起点将放入序列中;在另外50%概率下,保持全零序列不变;

3)将其它四个用电器作为干扰电器,均以25%的概率随机选取一次负荷激活(无需保证序列的完整),随机选择起点放入序列中。

根据实际多种用电器同时工作的情况,调整训练集中干扰电器的选取概率,使得模型更符合实际的负荷分解情境。本文对于每种电器构造400万条数据用作训练数据集。

3.5 实验评估指标

本文选择准确率、召回率、F1值、平均绝对误差作为评价模型的指标,计算方法如下:

(12)

式中Precision为准确率;Recll为召回率;F1代表F1分数,又称平衡F分数;TP表示用电器实际处于工作状态且模型分解结果也为工作状态的序列点总数;FP表示用电器实际处于工作状态但模型分解结果为非工作状态的序列点总数;FN表示用电器实际未工作但模型分解结果为在工作状态的序列点总数;yt为时刻用电器真实功率;ft(x)为t时刻模型分解功率,MAE为时间段T0到T1内功率分解值的平均绝对误差。Precision反映了模型预测用电器处于工作状态的精确度;Recall代表着正确召回用电器处于工作状态的概率;F1分数综合Precision和Recall反映模型判断用电器是否处于工作状态的准确度,是负荷分解的基本指标,前人的研究已经将其做到了较高的水平。MAE可以反映模型每时刻分解功率值的准确性,其值越低,则功率分解值的准确性越高。

3.6 实验评估指标

总功率经模型预测输出的分解功率与真实功率如图6所示,对于功率的跟踪效果比较好,仅在起始点与终止点的定位有所偏差,故分解功率值仍是非常高的。这也说明对于不同工作状态的电器具有良好的负荷分解能力。

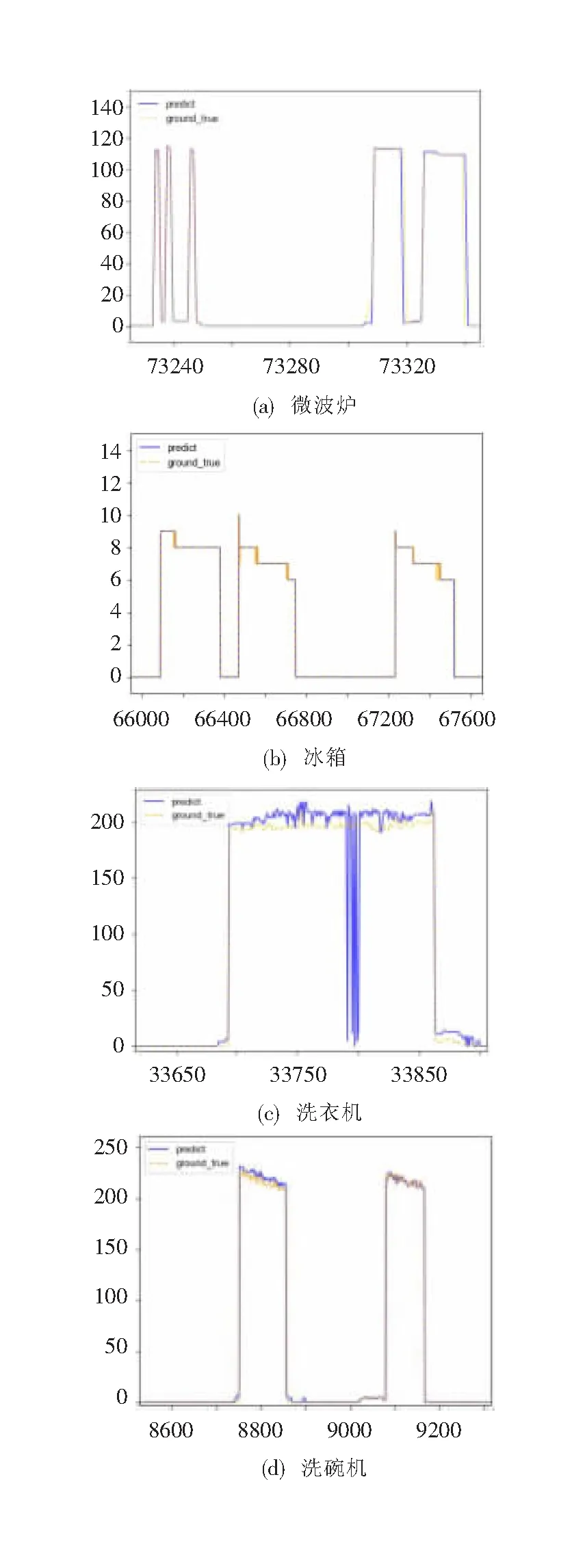
图6 各电器真实功率与模型分解功率对比

选取文献[13]所提出的LSTM模型与本文模型做训练时间上的对比,如表3所示,可以看出本文模型可以大幅度降低模型的训练时间测试结果总体如图7所示。

表3 模型训练耗时

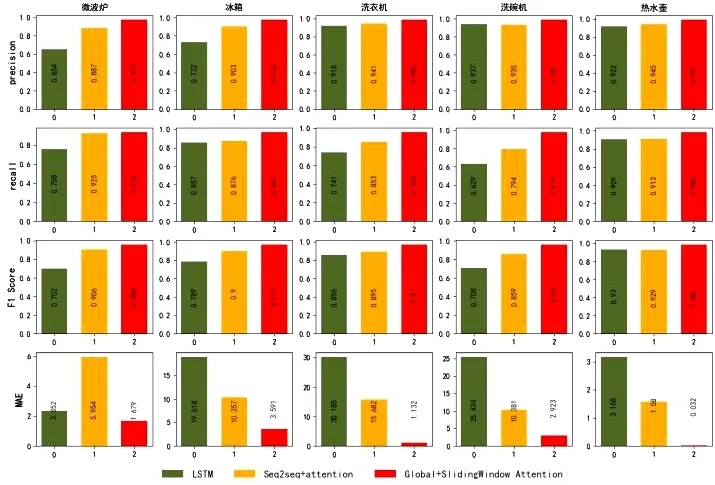
图7 测试结果

本文与文献[13]所提出的LSTM模型对比,准确率上有着较大的提高,可见本文所提模型对于多种工作状态的电器均有着优秀的建模能力。从滑动窗口,空洞滑动窗口,全局与滑动窗口结合的三种注意力机制来看,虽均有着较好的提升,但在全局与滑动窗口相结合的注意力机制更能全面而有效的提取长序列信息。

4 结束语

本文采用基于GSWA和Seq2seq的非侵入式负荷分解模型。该模型对Attention机制进行改善,将解码集中注意在与当前时刻相关度最高的编码层隐藏状态,在大幅提高模型分解功率准确值的同时,降低了模型计算量,加快了训练网络的速率。本文模型在准确率,召回率,F1值等指标上较前人均有提升,并显著降低训练时间。未来在对于提升网络的泛化能力以及对于小功率噪声的处理能力上开展研究。