基于空间插值算法确定离子型稀土矿体的底板
谢文强, 龙平, 胡世丽
(江西理工大学土木与测绘工程学院,江西 赣州 341000)
离子型稀土矿是我国重要的矿产资源,素有“工业维生素”和“工业黄金”之美誉,对现代高技术产业发展具有重要的作用[1]。离子型稀土矿的成矿条件极其复杂,花岗岩、火山岩、凝灰岩和混合岩等含稀土母岩,在温暖湿润的环境下,经物理、生物和化学等作用,母岩中的矿物相稀土转化为离子相形态,随着水流迁移,被黏土矿物吸附富集,形成离子型稀土矿[2]。目前,离子型稀土矿主要采用原地浸矿工艺进行开采[3]。原地浸矿是将浸矿剂溶液通过注液孔注入矿体,通过离子交换作用,将吸附在矿物表面的稀土离子解吸,形成稀土母液,稀土母液通过导流孔或巷道等收液工程收集,经过除杂、沉淀后实现稀土回收[4-6]。然而,该工艺在开采过程中常因矿体底板形状不明,导致注液、收液工程设计不合理,常出现收液率低,造成资源浪费、收液工程施工遇石返工耽误工期和反吸附严重等问题[7-9]。因此,准确确定离子型稀土矿体底板形状,对合理设计注液与收液工程、稀土资源回收和环境保护都具有重要意义。
地质勘探工作是当前探明矿体底板形状的有效手段[10],现场采用赣南钻进行勘探,通过钻孔打穿地表直至见水或见石处,以确定该勘探孔孔底的性质。然而,实际相邻勘探孔的间距较大,无法反映矿体底板局部区域的形状特征。因此,如何将有限勘探孔数据实现由点向面的转化,是确定矿体底板的有效方法。高原等[11]在径向基函数插值法的基础上,建立顾及地形特征的定权方法,有效反映了局部地形细节特征。申静等[12]将普通克里金法应用于海底地形的可视化表达。ZHANG等[13]提出的基于地形粗糙度的克里金法,相比传统的插值方法能显著提高插值效率与精度。李晓军等[14]对煤层底板进行贝叶斯地统计模型插值构造,认为该方法在地质层面高程预测方面具有一定的优越性。蒋伟达等[15]对埕岛海域地形演变进行多种插值方法分析,发现反距离权重法能更真实地反映该地区的水深地形。CHEN等[16]采用5种插值方法对不同粗糙程度的地形进行了评估,发现反距离权重法输出表面粗糙,难以体现地形细节特征。由此可见,空间插值方法在地质领域已被广泛运用,但基于空间插值算法确定离子型稀土矿体底板形状的研究较少。
本文采用常用的反距离权重法、径向基函数插值法、局部多项式法、普通克里金法和经验贝叶斯克里金法共5种空间插值方法,对离子型稀土矿体底板形状进行空间插值,利用独立数据集比较各方法的精度,分析稀土矿体底板的空间特征,为合理设计离子型稀土矿注液与收液工程提供指导。
1 实验部分
1.1 研究区域概况
试验场地位于福建省某离子型稀土矿山,该区域气候温和,雨水充沛,属于亚热带季风性气候,年均气温约18 ℃,年均降水量约1 700 mm[17]。该区域矿床母岩多以花岗岩为主,形成了储量较大、品位较高的离子型稀土矿,是我国南方重要的离子型稀土矿产资源富集区。
1.2 数据采集
勘探网度设置为约20 m×20 m,勘探孔直径设置为100 mm,采用赣南钻进行勘探工作。以潜水位或半风化层作为勘探孔的终孔依据,当勘探孔终孔至潜水位时标示孔底信息为见水,当勘探孔终孔至半风化层时标示孔底信息为见石,测量勘探孔深度。若某一勘探孔孔深明显小于周边的勘探孔,该位置可能遇到孤石,在附近再选一个位置进行勘探。该矿块共有440个见石勘探孔和39个见水勘探孔。采用GPS-RTK测量勘探孔孔口坐标,所有勘探孔的空间位置如图1所示。以见石勘探孔为研究对象,孔口高程减去相应勘探孔深度,即见石勘探孔孔底的高程。
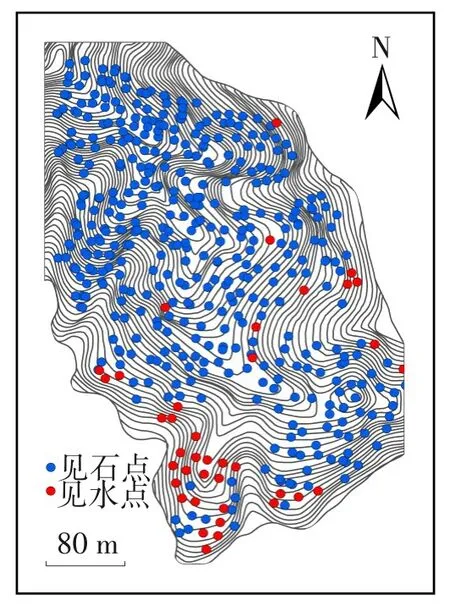
图1 福建省某离子型稀土矿勘探孔分布Fig.1 Distribution map of exploratory holes of an ionic rare earth ore in Fujian province
1.3 研究方法
采用泰森多边形聚类方法[18]对440个见石勘探孔孔底坐标数据进行离群检验,去除离群数据。基于莫兰指数[19]和K-S检验[20]对处理后的数据进行空间自相关性分析和正态性检验,判断是否具有正态性,能否进行地统计学方法分析,避免计算结果出现比例效应[18]。莫兰指数的取值范围为[-1,1],越趋近于1,说明数据的空间自相关性越好。通过K-S检验的P值判断数据是否服从正态分布,若P> 0.05,则服从正态分布;若P< 0.05,则不服从正态分布,需对数据进行转换,使其符合或基本符合正态分布。
分别随机取55%、65%、75%、85%和95% 5组数据作为训练点(数据点数按四舍五入取整),以其他数据作为检验点,通过反距离权重法[21]、径向基函数插值法[22]、局部多项式插值法[23]、普通克里金法[24](半变异函数为稳定函数)和经验贝叶斯克里金法[14]共5种空间插值方法分析训练点,预测检验点处的见石高程,以标准差(σ,式(1))、平均绝对误差(MAE,式(2))和均方根误差(RMSE,式(3))作为评价指标,量化检验点处高程预测值与实际值的误差。为了减少训练点选择的随机性对误差分析的影响,随机12次训练点,取12次检验点误差指标参数(σ、MAE、RMSE)的平均值作为每种方法的误差,根据误差值评价5种方法。
式(1)—式(3)中:N为样本数;Zcheck,i为实测高程;为预测高程为实测高程的平均值。
2 结果与讨论
2.1 数据点检验
440个见石勘探孔的聚类泰森多边形如图2所示,若某个多边形单元的级区间与其相邻单元的级区间都有所不同,则该单元的勘探孔为离群点,将离群单元用黑色表示,也绘制于图2中,本矿块的见石勘探孔共有15个离群点。将15个离群点去除,实际用于分析的见石勘探孔共有425个,离群处理后的见石勘探孔的聚类泰森多边形如图2(b)所示,由图2(b)可知,经过一次离群处理的数据,已经无新的离群点。

图2 离群值去除前(a)和去除后(b)的泰森多边形示意Fig.2 Schematic diagram of Tyson polygon before (a) and after (b) outlier removal
425个见石勘探孔的数据的莫兰指数为0.93,说明数据具有较高的空间自相关性,可应用地统计学方法进行空间插值分析。采用K-S检验分析勘探孔数据,得到P值为0.01(< 0.05),表明所分析的425个见石勘探孔数据不符合正态分布。运用对数变换对数据进行处理,在采用K-S检验进行分析,得到P值为0.06(> 0.05)。对数变换前,见石勘探孔高程频率分布直方图的偏度系数[25]为0.16;对数变换后,偏度系数为0.05。由此可见,采用对数转换处理后,可以提高数据的正态性,见石勘探孔高程数据可以视为正态分布(见图3 ),避免采用地统计学方法分析时的比例效应,保证了空间插值结果的精度。

图3 采用对数处理前(a)和后(b)见石勘探孔的频率分布直方图Fig.3 Frequency distribution histogram of stone exploratory holes before (a) and after (b) logarithmic processing
2.2 插值方法比较
从图4可知,5种插值方法的标准差(σ)、平均绝对误差(MAE)和均方根误差(RMSE)验证指标结果并不相同。随着检验点个数的增加,不同插值方法的精度均有所降低,总体上σ、MAE和RMSE随着检验点个数的增加而逐渐提升。在检验点个数相同的情况下,虽然5种插值方法在不同检验点个数的预测误差范围内均有所差异,但总体上径向基函数插值法的预测误差范围最小,其σ和RMSE均低于6.1,MAE低于4.9。由此可见,径向基函数插值法在插值精度上优于其他插值方法,预测效果更佳。

图4 检验点误差指标参数结果:(a) 标准差σ;(b) 平均绝对误差MAE;(c) 均方根误差RMSEFig.4 Parameter results of error index of checkpoints:(a) σ;(b) MAE;(c) RMSE
不同插值方法得到的稀土矿体底板空间形状格局大体相似,总体呈西北至东南方向逐渐降低的格局,但局部区域的细节特征及曲线平滑程度存在一定差异(见图5)。通过对比各插值方法的检验点误差分布(见图6),5种插值方法对区域 Ⅰ 内的见石勘探孔高程预测误差范围较大,主要是因为1号见石勘探孔(Z1=326.72 m)与相对邻近2号和3号(Z2=338.18 m,Z3=341.69 m)见石勘探孔实测高程相差颇远,极值点严重影响插值方法对局部区域的插值精度。各插值方法中,反距离权重法出现的频率相对更多,这是因为在插值过程中,该方法忽视各训练点之间的空间自相关性,仅以待测点附近训练点的距离大小,作为权重系数进行赋值,因而插值生成的拟合曲面极易受到极值点或点集群的影响,在局部区域内呈现孤立的“牛眼状”分布(见图6(a)),导致局部区域插值精度降低。

图5 基于5种插值方法生成的稀土矿体底板等值线:(a)反距离权重法;(b) 径向基函数插值法;(c) 局部多项式插值法;(d) 普通克里金法;(e) 经验贝叶斯克里金法Fig.5 Contour map of bottom plate of rare earth ore body based on five interpolation methods:(a)inverse distance weighting method;(b) radial basis function method;(c) local polynomial method;(d) ordinary Kriging method;(e) empirical Bayesian Kriging method

图6 检验点的误差分布:(a)反距离权重法;(b) 径向基函数插值法;(c) 局部多项式插值法;(d) 普通克里金法;(e) 经验贝叶斯克里金法Fig. 6 Error distribution of inspection point:(a)inverse distance weighting method;(b) radial basis function method;(c) local polynomial method;(d) ordinary Kriging method;(e) empirical Bayesian Kriging method
高程变化明显的区域也是各插值产生偏差的原因。在区域 Ⅱ 中,4号、5号和6号见石勘探孔高程(Z4=368.36 m,Z5=370.83 m,Z6=378.05 m)由东南至西北方向逐渐升高,该区域各插值方法的预测误差较其他平稳区域相差较大,表明各插值方法拟合形成的曲面均受到高程变化而影响精度。经验贝叶斯克里金法虽然通过利用训练点数据能模拟多个半变异函数进行插值分析,以此提高插值精度,但由图5(e)可知,该方法生成的预测表面过于平滑,难以反映局部高程区域的细节变化,而相比于插值精度最高的径向基函数插值法,该方法具备对训练点数据拟合程度高、生成预测表面平滑能力强等优点,能凸显矿体底板高程的变化幅度,对高程变化波动较大的数据,插值精度通常较高,能较好地反映底板局部变化特征与趋势。然而,径向基函数并非总体最优,相对局部训练点空白区域 Ⅲ 而言,该区域径向基函数插值法相比反距离权重法误差范围更大,表明在处理无训练点区域,径向基函数插值法插值精度相对较低。
此外,四周边缘区域缺少训练点数据作为参考,对稀土矿体底板预测空间分布也会造成较大的影响。从区域 Ⅳ 可知,8号和9号见石勘探孔分布在矿区的右边缘处,相比于中间区域,该区域训练点进行插值时,插值精度会受到周边训练点数目的影响。通过对比各插值方法的误差分布,局部多项式插值法和普通克里金法因边缘区域缺少足够的训练点数据,在区域的边缘化问题中,易产生更大的误差,造成周边区域插值精度降低,这与费坤等[21]的研究相吻合。
由此可见,虽然在局部训练点空白区域,径向基函数插值法的插值精度低于反距离权重法,但总体在插值精度或是插值效果上都优于其他方法,采用径向基函数插值法是确定离子型稀土矿体底板空间形状较好的方法。
3 结 论
本文基于有限的见石勘探孔高程数据,采用空间插值算法确定离子型稀土矿体底板形状,并通过标准差、平均绝对误差和均方根误差分析各种方法的精度,在此过程中得到以下结论:
1)去除离群点和对数处理后,见石勘探孔数据的莫兰指数和P值分别为0.93和0.06,说明对数处理后数据具有较好的空间自相关性和正态分布特性,能用地统计学插值方法进行分析。
2)随着检验点的增多,检验点的σ、RMSE和MAE均呈增加趋势,当检验点占比超过35%时,σ、RMSE和MAE量化参数趋于稳定。
3)径向基函数插值法的σ和RMSE均低于6.1以下,MAE低于4.9,总体插值精度和插值效果都优于其他插值方法,能更好地呈现离子型稀土矿体底板总体形状和局部变化的细节特征。

