基于断层影响下的充填体强度需求优化研究

李广波， 盛宇航， 吴再海， 宋泽普

（1.山东黄金矿业股份有限公司， 济南 250100； 2.山东黄金矿业科技有限公司充填工程实验室分公司，山东 莱州 261441）

随着金属矿山逐渐进入深井开采，充填采矿法得到广泛应用，充填体与矿体的变形破坏过程变得越来越复杂，研究其相互作用具有重要意义，特别是开采至断层处存在应力释放的风险[1-4]。当工作面向断层推进时，断层的构造应力与工作面超前支承压力叠加，形成的高应力集中作用于两侧的充填体及矿体上[5-6]。目前，研究者对充填体与矿体相互作用、断层影响下的围岩失稳机理等开展了大量研究。吴爱祥等[7]利用Belem模型分析计算了充填体3种应力状态下的目标强度，对比拱架效应引入前后充填体垂直应力降低比率。刘光生等[8-9]基于实际采充时序过程，考虑充填体与矿体接触作用，提出了充填体强度要求修正解析方法，并采用FLAC3D进行验证。还有研究者采用3种力学理论模型进行了分层胶结充填体强度需求解析计算，得到了胶结充填体强度与充填次数之间的数学模型及折减系数[10-11]；利用数值模拟、物理模型、解析公式和现场监测等方法对充填体成拱作用和应力分布进行研究[12-15]。目前的研究大多只考虑单一因素，并没有考虑断层对于充填体强度需求的影响，使得采场回采至上盘断层附近，因断层不稳固极易导致塌落[16-20]。现场施工时，经常出现2种情况，一是为保证安全偏离上盘断层较远，导致矿体损失；二是沿上盘断层施工时，上盘暴露面积过大，矿柱位置选择不合理，导致上盘塌落，矿体难以采出。

本文针对以上不足，以山东某矿的断层赋存特点为研究对象，首先根据该矿采场尺寸和充填体与矿体的物理力学参数，开展断层处充填体与矿体的两步采力学分析，确定出合理的充填体强度需求解析解；再利用FLAC3D建立采场三维数值模型，对两步采过程中断层处的充填体与矿体稳固性进行模拟研究，得到采充过程中两步采采场充填体强度需求数值解，对比研究充填体强度需求解析解、数值解和实际生产值，校验修正解析模型的可靠性，保证断层处矿体安全高效开采。

1 工程背景

该矿原设计的充填体强度及矿柱尺寸，主要是利用同类矿山经验类比选取的强度指标，导致矿山存在充填强度设计不合理、充填成本居高不下等问题。为了有效解决矿山面临的生产难题，本文选择该矿100线以北、116线以南矿体进行断层影响下的充填体强度需求研究。

1.1 矿体特征

该矿床属于第四系松散沉积物广泛分布，主断层倾角55°，落差2 m，矿体上盘主要为绢英岩，下盘主要为闪长岩，在断裂面上发育有一层厚约0.2 m的黑色断层泥。矿体上盘与围岩为断层接触关系，界线明显；而矿体下盘与围岩呈渐变过渡关系，无明显的边界线。断层两侧矿体受其影响，强度明显降低，破碎程度增大，并有一定的似层状特点，施工至断层处时极易发生冒顶、片帮等安全事故，所以亟需解决充填体强度需求问题。

1.2 采矿方法

由于矿区周边临近农田和村庄，同时结合矿体赋存条件，经综合考虑采用上向水平分层充填采矿法，按隔一采一顺序沿矿体走向先采矿房，出矿后胶结充填，再按顺序依次进行相邻两侧两步采采场回采，如图1所示。采场埋深600 m，走向长度120 m，倾向长度为80～100 m。

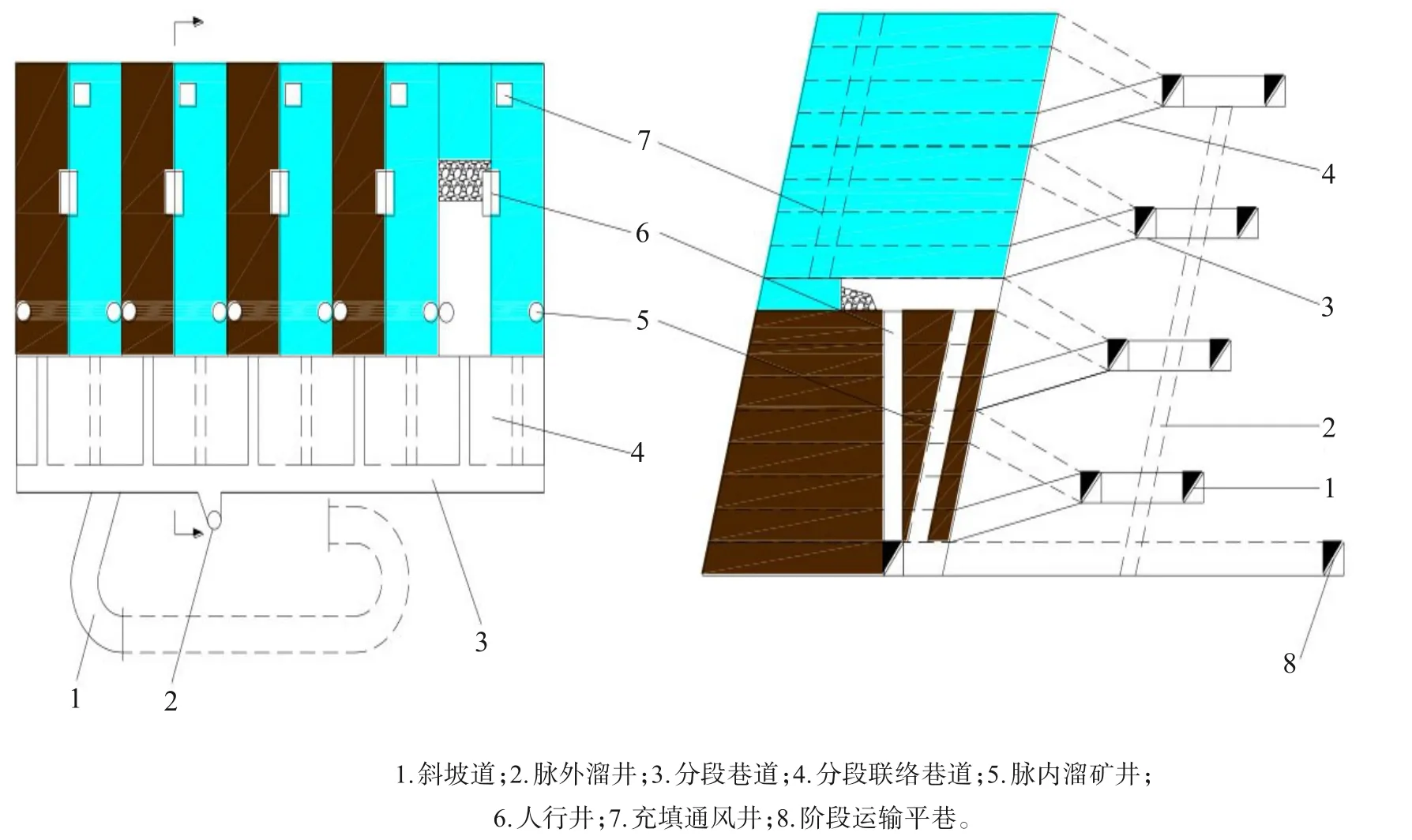
图1 盘区式上向水平分层充填法Fig.1 Panel upward cut and fill method

2 基于断层影响下的充填体强度需求力学分析

目前，对充填体力学特性的研究逐渐增多，但国内矿山仍然以经验类比进行充填强度计算研究，导致国内同类型矿山的充填水泥单耗远大于国外。针对该矿地质赋存条件，矿体整体较为破碎，特别是临近断层时两侧矿体受断层影响，强度明显降低，破碎程度增大，极易发生冒顶、片帮等安全事故。

本文进行充填体强度要求解析计算时，重点研究两步采回采过程中断层处力学模型。在两步采采场回采过程中，断层与相邻矿体、充填体并不是孤立存在的，受上盘岩体和断层两侧胶结充填体的夹制，以此进行两步采采场揭露前后胶结充填体的应力计算，如图2所示。

图2 两步采回采时断层力学分析Fig.2 Mechanical analysis of fault in two step mining

考虑充填体与矿体接触作用以及断层受到一步采采场充填体的水平挤压力，断层两侧壁接触面产生相应摩擦力，对断层进行应力平衡分析，得到：

式（1）中：W上盘为上盘岩体作用于两步采断层处的挤压力，单位kN；W断为断层自身重力，单位kN；f1为断层受到两侧壁的一步采采场胶结充填体水平挤压力产生的摩擦力，单位kN；ϕ断为断层的倾角，单位（°）。

上盘矿体的重力W上盘为：

式（2）中：γ1是上盘岩体的容重；h埋为矿体埋深高度；B和H为矿房的宽度和高度。由于上盘岩层较厚大，只考虑其投影等效面积。

断层的局部自重为：

式（3）中：γ2是断层的容重；h断为断层的厚度。

断层受到两侧壁的一步采采场胶结充填体摩擦力f1计算如下：

式（4）中：cs为接触面内聚力；H为矿房的高度。

假设采场岩壁十分粗糙，接触面内聚力cs与充填体内聚力c相等[21-23]，则胶结充填体内聚力c为：

假设充填体服从直线型摩尔库仑准则，则充填体内聚力c与单轴抗压强度σc的关系满足：

式（6）中：ϕc为一步采胶结充填体的内摩擦角，单位（°）。

将式（5）代入式（6）后，计算得出充填体单轴抗压强度σc：

将矿山采场尺寸及充填体参数γ1=26.87 kN/m3、γ2=15.47 kN/m3、B=4 m、H=5 m、ϕ断=55°、h断=0.2 m、h埋= 600 m、ϕc=30°代入式（7），可得极限平衡状态两步采采场回采时充填体强度需求解析解σc=2.85 MPa。

为进一步对比采场两步采过程中断层处充填体强度需求，需要利用FLAC3D建立采场三维数值模型，对两步采过程中断层处的充填体与矿体稳固性进行数值模拟研究，得到采场两步采过程中充填体强度需求数值解，将充填体强度需求解析解和数值解进行对比研究。

3 基于断层影响下的充填体与矿体数值模拟分析

3.1 模型建立

该矿经过岩石分级评价、钻探取芯和室内力学实验等后，得到各岩体的物理力学参数，如表1所列；同时，利用该矿的分级尾砂和胶凝材料开展充填体配比实验（质量浓度为68%），得到不同灰砂比充填体物理力学参数，如表2所列。

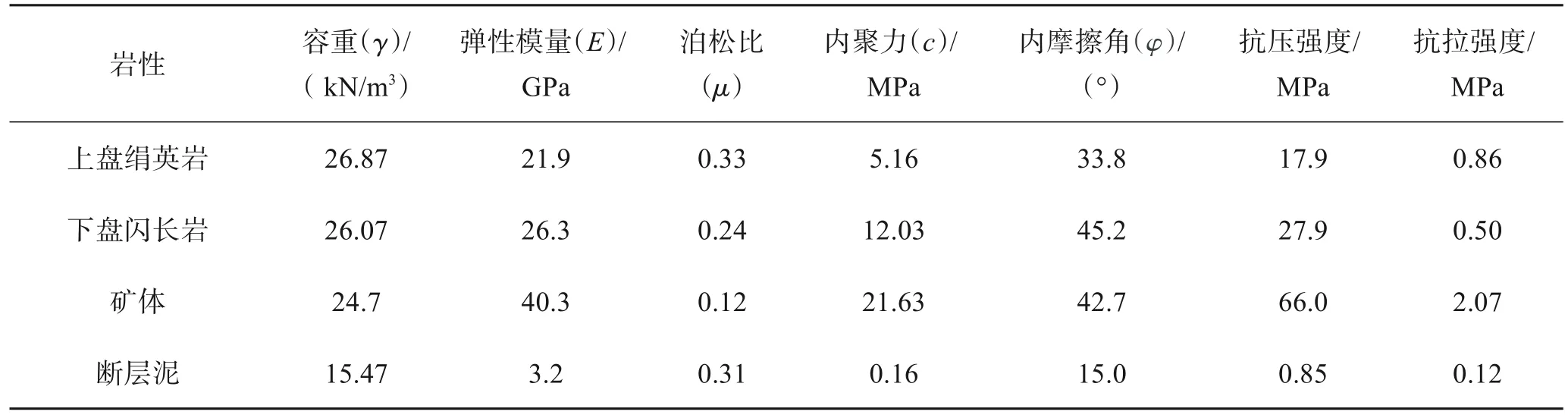
表1 各岩体物理力学参数表Table 1 Table of physical and mechanical parameters of rock masses

表2 不同灰砂比充填体物理力学参数表Table 2 Physical and mechanical parameters of filling body with different lime sand ratio

在前人研究的基础上，结合该矿的地质赋存条件和物理力学参数，建立断层与采场的数值计算模型，模型尺寸为300 m×200 m×100 m，如图3所示。计算采用摩尔库仑准则。

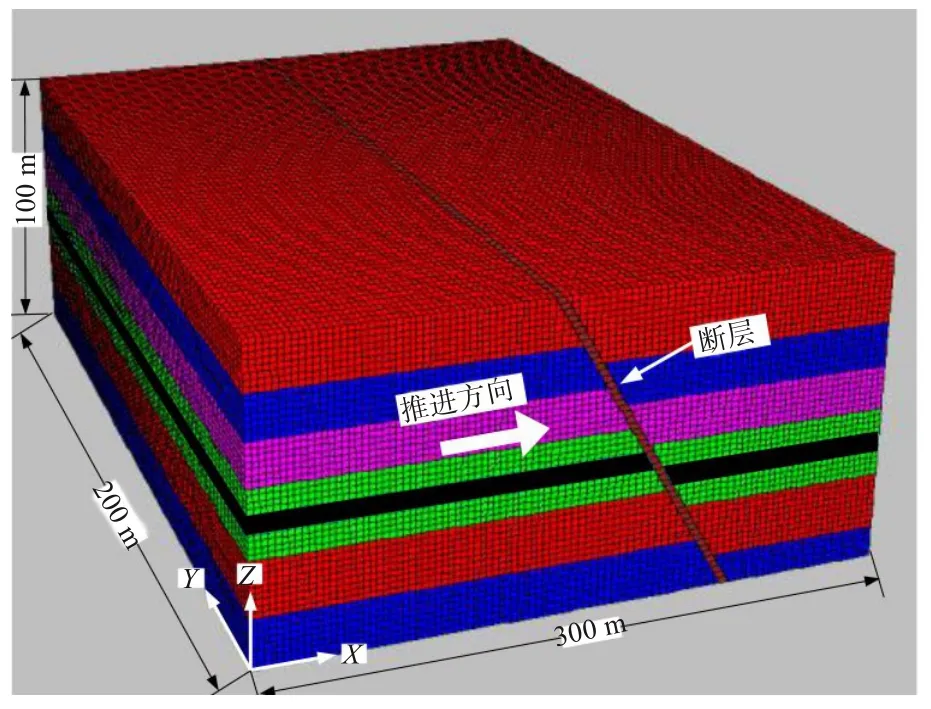
图3 断层计算三维模型Fig.3 3D model of fault calculation

边界条件为：模型Z方向上部为自由面，施加15 MPa的均布荷载，模拟上覆岩层600 m的自重荷载；模型X方向施加最大水平主应力17.72 MPa；Y方向施加最小水平主应力13.45 MPa。模型Z方向下部限制垂直方向位移，模型X、Y方向限制水平移动，工作面布置在断层下盘中。采场规格为长×宽×高=100 m×4 m×5 m，断层倾角55°。

开挖顺序为：①一步采：按照隔一采一顺序沿X轴正方向推进，分步开挖20、40、60、80、90 m，逐步向断层推进，记录断层处应力和位移变化情况，达到计算平衡后，将模型中的弹性位移清零（实际采场开挖后围岩的弹性位移在充填之前己基本释放完成）。②充填：开挖空间充填模拟时，采用多层充填加载方式，模拟矿山实际充填情况对开挖空间重新赋值（底部1 m采用质量浓度68%、灰砂质量比1∶4进行充填；接顶0.5 m采用质量浓度68%、灰砂质量比1∶10进行充填；中间层采用质量浓度68%、灰砂质量比1∶20进行充填）。待模型重新计算平衡后，进行两步采回采。③两步采：按顺序依次进行相邻两侧两步采采场的回采，分步开挖20、40、60、80、90 m，逐步向断层推进，记录断层处应力和位移变化情况，如图4所示。

图4 开挖示意图Fig.4 Schematic Diagram of Excavation

3.2 一步采——工作面推进至距断层不同距离应力演化规律

一步采回采过程中，工作面推进至距断层不同距离应力演化规律如图5所示。

图5 一步采过程中工作面推进至距断层不同距离处应力云图：（a） 80 m；（b） 60 m；（c） 40 m；（d） 20 m；（e） 10 mFig.5 Stress nephogram of working face advancing to different distances from the fault in one-step mining process：（a） 80 m；（b） 60 m；（c） 40 m；（d） 20 m；（e） 10 m

由图5可知，一步采回采矿体时，原岩应力的平衡状态被打破，应力重新分布，造成相邻的矿体应力集中。随着一步采工作面的推进，工作面顶底板垂直应力集中程度进一步增加，在工作面端部及两侧帮1～5 m处形成规则的应力集中区，当工作面距断层距离分别为80、60、40、20、10 m时，工作面端部的垂直应力值依次分别为2.72、3.65、4.57、5.29、4.21 MPa，两侧帮的垂直应力值依次分别为1.98、2.57、2.92、3.53、4.15 MPa。

由此可以看出，随着工作面的推进，工作面端部及两侧帮应力逐渐增加，当工作面推进至距断层10 m处，应力集中程度有减弱的趋势，工作面端部应力集中区与断层贯通，说明此处极易发生断层垮落等事故。

3.3 两步采——工作面推进至距断层不同距离应力演化规律

两步采回采过程中，工作面推进至距断层不同距离应力演化规律如图6所示。

图6 两步采过程中工作面推进至距断层不同距离处应力云图：（a） 80 m；（b） 60 m；（c） 40 m；（d） 20 m；（e） 10 mFig.6 Stress nephogram of working face advancing to different distances from the fault in two-step mining process：（a） 80 m；（b） 60 m；（c） 40 m；（d） 20 m；（e） 10 m

由图6可知：一步采采空区胶结充填后，两侧的充填体与矿体形成应力的二次平衡状态，此时胶结充填体既能够限制矿体的变形，又能够与矿体共同承载。随着两步采回采矿体，造成应力的二次分布。随着两步采工作面的推进，工作面顶底板及两侧帮垂直应力较开挖前明显减小，应力集中区向外移动。当工作面距断层距离分别为80、60、40、20、10 m时，工作面端部的垂直应力值依次分别为1.65、2.37、3.25、4.43、2.91 MPa，两侧帮的垂直应力值依次分别为1.47、1.95、2.61、2.88、2.97 MPa。与一步采应力值相比可知，一步采胶结充填体可减轻采场断层处因应力集中而导致的破坏，进而为采场安全施工及矿柱回采提供便利。

对比图6（c）和图6（d）可知：随着工作面的推进，工作面端部和两侧帮应力同样逐渐增加，当工作面推进至距断层20 m处，工作面端部应力集中区与断层应力集中区贯通，说明此时充填体可能已处于失稳状态，据此得出了该矿两步采的充填体强度需求解析解2.97 MPa。同时，由图6（d）和图6（e）可以明显看出，断层对于应力传递起到阻隔作用，在工作面上方30 m处形成应力释放区。

3.4 矿山充填体强度需求对比

通过上述研究分别得到该矿断层影响下两步采采场采充过程中充填体强度需求的解析解和数值解，对比可知解析解和数值解吻合度较好，说明基于断层影响下的充填体强度需求模型和数值模拟可以很好地计算两步采采场充填体的强度需求。经矿山调研，该矿充填质量管理规定根据经验公式求得，要求采场充填体强度大于两者，如表3所列。

表3 3种方式充填体强度需求Table 3 Strength requirements of three filling methods

为了进一步验证优化满足矿山充填开采技术现状的采场充填体实际强度需求，下一步将与矿方沟通进行试验采场验证。

4 结 论

1）通过对断层处的充填体和矿体进行力学分析，建立基于断层影响下的充填体强度需求力学模型，推导获得了极限平衡条件下充填体强度需求计算公式，得到了该矿二步采的充填体强度需求解析解为2.85 MPa。

2）利用FLAC3D构建了两步采回采充填体与矿体的数值计算模型，可以看出：随着工作面的推进，工作面端部及两侧帮应力逐渐增加，当工作面推进至距断层10～20 m处，应力集中程度有减弱的趋势，工作面前端应力集中区与断层贯通，得到了该矿两步采的充填体强度需求解析解为2.97 MPa。

3）通过进行充填体强度需求解析解和数值解对比，进一步验证了基于断层影响下的充填体强度需求力学模型的有效性；但矿山实际充填强度要求大于两者，需进一步验证优化。

4）虽然本文所建立的力学模型可以反映充填体内应力演化规律，但以上研究只涉及了力学推导和数值模拟等理论验证，未开展现场充填体应力监测验证，下一步通过开展现场应力监测来进一步验证力学模型的有效性。