复合材料高温力学性能自动化测试关键技术研究与系统设计
周翔 马占东 国凯 刘晓菲 马宝庆
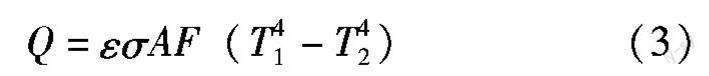
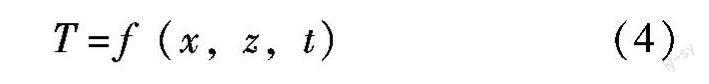
摘 要 针对传统人工操作模式下复合材料高温力学性能测试效率低、检测质量差、温控精度低的问题,本文设计了面向复合材料压缩测试的自动送样-测试-取样多模块测试系统,研究了封闭条件下环境箱温度场建模与补偿技术,建立了温度补偿模型,并设计高精度温度控制器,实现了对温度的精准补偿与控制;开展自动化测试系统的运动学和动力学建模研究,完成动力学参数在线辨识,在此基础上设计自动化测试系统自适应控制器,最后进行了控制实验。实验结果表明,神经网络自适应控制器可以实现系统的高精度控制,跟踪精度和定位精度均满足自动化测试要求。
关键词 复合材料;高温环境;力学性能;自动控制
Research on Key Technologies and System Design of
Automatic Testing of High Temperature Mechanical
Properties of Composite Materials
ZHOU Xiang1,MA Zhandong1,GUO Kai2,LIU Xiaofei1,MA Baoqing1
(1.AVIC Research Institute for Special Structures of Aeronautical Composite, Aviation Key Lab
of Science and Technology on High Performance Electromagnetic Windows, Jinan 250023;
2.Department of Mechanical Engineering, Shandong University, Jinan 250061)
ABSTRACT Aiming at the problems of low efficiency, poor detection quality and low temperature control accuracy of high temperature mechanical properties testing of composite materials under the traditional manual operation mode. In this paper, an automatic send-test-sample multi-module test system for composite materials compression testing was designed. The modeling and compensation technology of ambient box temperature field under closed conditions was studied. And a temperature compensation model was established, also a high-precision temperature controller was designed to achieve accurate compensation and control of temperature. The kinematics and dynamic modeling research of the automatic test system was carried out, the online identification of dynamic parameters was completed, and the adaptive controller of the automatic test system was designed on this basis, and finally the control experiment was carried out. The results showed that the neural network adaptive controller could achieve high-precision control of the system, and the tracking accuracy and positioning accuracy met the requirements of automated testing.
KEYWORDS composite materials, high temperature environment, mechanical properties, automatic control
通訊作者:周翔,工程硕士,高级工程师。研究方向为复合材料测试技术。E-mail: zhouxiang217@163.com
1 引言
复合材料具有比强度高、比模量高、可设计性强、耐高温、耐腐蚀、抗疲劳性能好等优点,在航空航天领域应用广泛,先进复合材料质量占飞机结构总质量的多少,在某种程度上已经成为评价该飞机技术先进程度和市场竞争力的重要指标[1-2]。随着航空工业的飞速发展,以军用武器装备为代表的高技术产品的需求量日益提高,军用武器装备产品所使用材料性能测试需求日益增大,传统的人工检测、测试手段已经无法满足现代化装备的支持保障测试效率的要求,自动化测试设备及系统正逐步成为大批量测试可靠运行的必要保证。近年来,自动化测试系统已经在设备故障诊断、精密机械加工、环境监测等多个领域获得广泛应用,特别是以军事领域强有力的需求为牵引,自动测试技术和自动测试设备发展十分迅速,已经成为国防建设和生产生活中不可或缺的重要组成部分。
近年来国内外研究人员对复合材料的高温拉伸[3-6]、剪切[7-9]、弯曲[10-14]性能进行了大量研究,取得了一系列优异成果,然而相关的实验设备大多采用人工操作,自动化程度低,检测稳定性难以保证。具体表现在以下几个方面:(1)封闭条件下环境箱温度场复杂多变,温度控制具有延迟性,控制精度低;(2)现有测量技术检测过程人员参与量大,人为操作误差大;(3)现有高温材料力学性能测试设备发展缓慢,智能化程度低,缺少自动化检测关键技术。由于以上问题的综合影响,在目前的人工操作模式下,复合材料高温力学性能检测在送样、加热、检测等环节严重影响着检测精度及质量,降低了检测效率。此外,高温环境箱需要绝热环境,频繁的开关环境箱门放置复合材料试样不仅会导致检测效率低下,而且会造成能源浪费。
本文综合了目前复合材料力学性能测试装置的研发与实验研究状况,针对高温环境下材料力学性能自动化测试需求,研制了自动化测试装置;研究了封闭条件下高温环境温度场建模及补偿技术,针对温度控制具有滞后性、温度分布不均匀等特性,深入研究了封闭环境下传热机理、温度调节与补偿技术,提高温度场均匀性,提高加热效率,缩短加热时间;针对目前自动送样测试系统存在智能化程度低、控制精度低、对不同规格待测材料适应性差等问题,研究了具有强适应性、高稳定性的新型控制方法,使用神经网络重构自动测试系统动力学模型,完成未知动力学参数在线辨识,设计了自动化测试系统自适应控制器,并进行了控制对比实验,验证了测试系统的优良控制性能。
2 自动化测试系统总体设计
2.1 测试系统总体设计
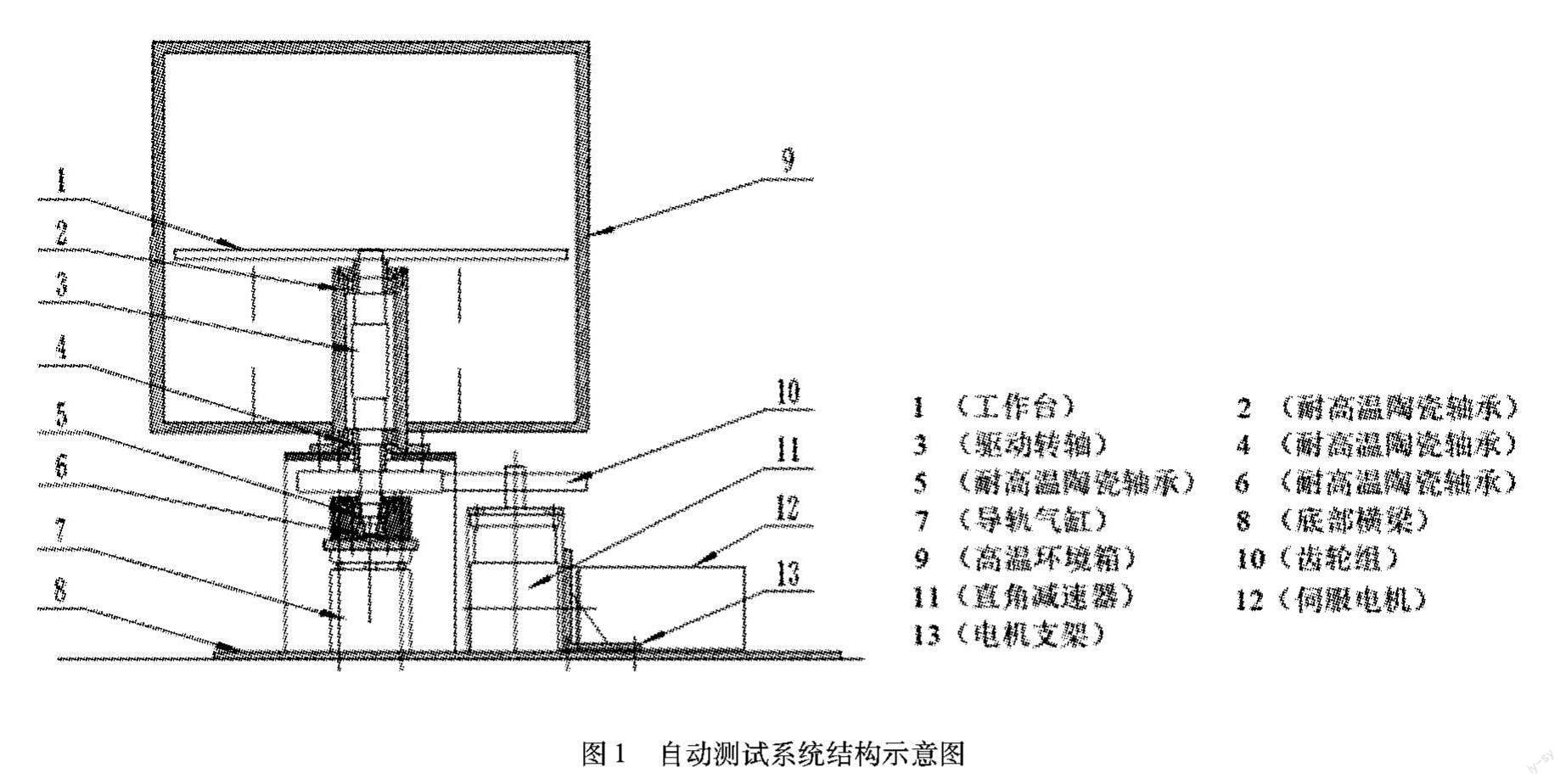
复合材料高温力学性能测试实验装置主要由高温环境箱、上压头和下压头三个部分组成,复合材料试样放于下压头上进行高温压缩力学性能测试,通过下压可以实现复合材料的压缩、弯曲、层间剪切等测试项目。设计的主要思路是先分析复合材料压缩测试的大致过程,再拟定出自动送料-测试-取样的实现方式。测试系统主要由工作台、伺服电机、减速器、齿轮组、导轨气缸和传动机构等部分组成,系统具有2个自由度,具体包括工作台的旋转运动,完成试样的旋转送料,以及驱动转轴的上下浮动,对应完成工作台的升降移动,系统整体结构示意图如图1所示。伺服电机12由电机支架13固定在底部横梁8上,经直角减速器11和齿轮组10减速后,驱动转轴3和工作台1旋转,实现复合材料试样旋转送料。气缸7由螺栓固定在底部横梁8上,通过推出和回缩实现工作台1在高温环境箱9内部的升降移动。自动测试系统均选用耐高温陶瓷轴承,使用温度范围宽,弹性模量高,不易因受力而导致变形,并可降低转动时的摩擦,延长装置整体使用寿命。
2.2 自动化测试工作流程
自动测试系统工作流程为:(1)当复合材料试样压缩实验完成后,由导轨气缸7推动转轴3和工作台1向上移动,使工作台1脱离下压头。(2)伺服电机12经过直角减速器11和齿轮組10减速后,带动转轴3和工作台1旋转,实现复合材料试样换料。(3)由导轨气缸7推动转轴3和工作台1向下移动,使工作台1紧贴下压头,进行新的复合材料试样的压缩。(4)重复以上步骤,直至工作台上本批次6个试样全部完成测试。系统详细工作流程图如图2所示。
上压头直径为80mm,环境箱宽度为400mm,为充分保证工作台的活动空间,工作台与环境箱内壁间隙设置为10mm,圆形工作台直径取380mm,厚度取为8mm。环境箱及工作台的具体尺寸布置如图3所示。
工作台设计6个工位,沿工作台周向间隔60°均匀分布,如图4所示,试样设有定位槽,定位槽分布圆直径为300mm,可实现复合材料试样的定位。
3 封闭条件高温环境温度场建模及补偿
3.1 环境箱温度场介绍
高温力学性能测试系统为封闭环境,高温环境下的温度控制精度对复合材料的力学性能测试有着重要的影响,直接决定测试精度及测试效率。温度控制具有滞后性、温度分布不均匀等特性,通过研究封闭环境下传热机理、温度调节与补偿技术,提高温度场均匀性,提高加热效率,缩短加热时间。环境箱的温度场建模及补偿技术,主要由以下三部分构成:
(1)分析环境箱结构,建立环境箱的三维物理模型和适用于有限元分析的二维传热简化模型,完成传热模型的离散化和网格划分,通过有限元分析环境箱温度变化。
(2)构建封闭环境中的瞬态传热微分方程,设置与环境箱实际热传导相符的边界条件,采用Matlab-PDE工具箱通过有限元法求解微分方程,获得环境箱中温度场的温度梯度及热流矢量,揭示时变状态下环境箱中温升特性。
(3)根据环境箱的温升模型设计高精度温度控制器,引入Smith补偿控制方法以加快系统滞后环节补偿速度,实现复合材料在环境箱中温度的精准补偿及控制。
3.2 环境箱模型构建
环境箱通常由加热模块、保温模块、循环模块和温度监测模块组成。目前使用的环境箱中,加热模块为5KW电阻丝阵列,位于箱体后方;保温模块由不锈钢箱体外壁及保温材料构成,具有良好的保温性能;循环模块为箱体后方电阻丝上方的循环风扇,它引起空气的强制对流;此环境箱中还有用于试样测试的金属工作台,其金属结构与外界连通,发生自然散热;温度监测模块布置于工作台中,其尽可能贴近被测试样的安装位置,可一定程度上提高温度测量的准确性。
抽象并简化环境箱中发生热量交换的主要结构,建立如图5所示的环境箱三维物理模型。工作台、上下压头及送样机构仅保留支撑杆和圆柱形主体结构,圆角、凸台等复杂结构均被忽略。环境箱工作时,电阻丝升温,作为系统热源实现环境箱内部的温升,循环风扇促进箱体内热空气的流动,加速升温过程并使温度场中的温度分布均匀,工作台和保温箱体持续向外散失热量。
为降低计算难度,提高仿真效率,将环境箱的三维物理模型进一步简化为如图6所示的二维传热模型,此二维模型以三维模型在x-z对称面上的投影为基础构建,可准确反映真实的温度场和热量交换情况。
使用Matlab-PDE工具箱对二维模型进行网格划分,网格类型设置为三角形网格,最大网格尺寸为0.005m,形成二维网格如图7所示,其中网格数为27968,节点数为56387。
至此完成环境箱模型的构建,在此模型的基础上通过有限元方法研究环境箱的温度分布和温升特性,并建立相应的温度控制及补偿策略。
3.3 环境箱温升特性研究
热量的传递包括热传导、热对流和热辐射三种基本形式。其中,热传导是物体各部分依靠分子、原子和自由电子的热运动所产生的热量传递,遵循傅里叶导热定律,如公式(1)所示。
式中,q*为热流密度,单位为W/m2;k为导热系数,单位为W/(m·K);?T/?x、?T/?z分别为沿x、z方向的温度梯度,负号表示热流量始终指向温度减小的方向。环境箱中热传导主要存在于电阻丝与附近空气、高温空气与低温空气之间。
热对流指固体表面与其周围的流体之间,由于温差存在而引起的热量交换,对流可分为自然对流和强制对流,一般作为边界条件施加。热对流可用牛顿冷却方程进行描述,如公式(2)所示。
式中,hf为对流换热系数,单位为W/(m2·K);Ts为固体表面的温度,单位为K;TB为周围流体的温度,单位为K。环境箱中热对流主要存在于空气与工作台、箱体外壁之间。
热辐射指物体发射电磁能,并被其他物体吸收转变为热能的热量交换过程,物体温度越高,热辐射越强。不同于需要传热介质的热传导和热对流,热辐射的进行无需任何介质。通常使用斯蒂芬-玻尔兹曼方程计算热辐射,如公式(3)所示。
式中,Q为热流率,单位为KW/℃;ε为辐射率,σ为斯蒂芬-玻尔兹曼常数,约为5.67×10-8W/(m2·K4);A为辐射体面积,单位为m2;F为形状系数,T1,T2分别为辐射体和被辐射体的热力学温度,单位为K。环境箱中的热辐射主要存在于箱体外壁与外部环境之间。基于三种基本传热形式,可构建环境箱的温度场函数如公式(4)所示。
式中,x、z分别为空间坐标,t为时间坐标。
根据傅里叶导热定律和能量守恒定律得到环境箱在空间x,z方向上的二维传热模型,如公式(5)所示。
式中,?为环境箱电阻丝的热源强度,单位为W/m3;kx,kz分别为材料沿x,z方向的导热系数,T0为环境箱的初始温度。
根据对环境箱结构的分析,设置环境箱温度场仿真中各系统结构的属性及边界条件如下:箱中空气:密度1.293kg/m3,導热系数0.0242W/(m·K);工作台及压头:密度7850kg/m3,导热系数48.85W/(m·K);电阻丝:设置温升曲线为T=Td·(e-3s/5s+1)℃,进入稳态阶段后看作恒温热源;循环风扇:强制对流边界条件,对流换热系数为100W/(m2·K);保温箱体:热辐射边界条件,辐射率为0.1。
最后,在仿真中将外界环境温度和环境箱各部分的初始温度均设置为30℃,热源温度设置为200℃,时间步长设置为1s,仿真时长500s。通过Matlab-PDE工具箱和传热模型网格完成环境箱求解升温过程中各时刻温度场分布情况,得到的环境箱温升过程温度场变化情况如图8所示。
为便于查看工作台附近的温度变化情况,于工作台附近布置测温阵列,测温点位布置为:工作台底部4个测点(-0.06,0.2)、(0.06,0.2)、(-0.15,0.2)、(0.15,0.2),中心位置1个测点(0,0.3),上方4个测点(-0.06,0.3)、(0.06,0.3)、(-0.15,0.3)、(0.15,0.3),依次编号为测点1-9。计算得到测点在环境箱温升过程中的温度变化曲线,如图9所示。它体现了待测的复合材料周围的温度变化,是环境箱的重要性能评价指标。
由图9可知,在温升的仿真过程中,经过约450s的加热后环境箱温度场达到稳态,由于工作台与环境箱体外壁等处的热量散失,工作台附近温度与热源之间存在约20℃的稳态误差。以九个测点温度数据的均值为基准,使用Matlab系统辨识工具箱对仿真数据进行拟合,得到包含延迟环节的环境箱温升特性模型,如公式(6)所示。
温升模型的响应曲线与环境箱温升仿真数据的对比如图10所示,可见其较准确地重现了环境箱的温升过程,可反应环境箱的温升特性。
3.4 环境箱温度控制及补偿策略
通过对环境箱温升过程中温度场变化的仿真和工作台附近温度的监测情况可知,若不进行外部调控,则环境箱温度调整需要较长时间,调整完成后相对于热源温度也有较大的稳态误差。因此,必须设计有效的控制器对环境箱温度进行控制和补偿。
工业中最常使用的控制器为PID控制器,它具有良好的鲁棒性,可对绝大多数系统做出有效的控制[15],因此首先为环境箱设计PID控制器,其闭环控制结构如图11所示。
依据环境箱温升特性模型和实际控制效果整定PID控制器参数。设置环境箱中工作台周围的理想温度为200℃,得到控制效果较好的一组参数为:Kp=2.2,Ki=0.1,Kd=2.8。PID控制器对于九个测点平均温度的控制结果和无控制器时环境箱内温度测点的变化情况如图12所示。
由图12可知,PID控制器的引入明显加快了环境箱内的温升过程,约390s时环境箱内温度即满足要求,温度控制的稳态误差基本完全消除。但是,由于环境箱温升过程中系统存在滞后环节,PID控制器对调温动态过程的改善受到较大限制,温度调节起始阶段的延迟难以得到改善,并且引入PID控制器后工作台附近的温度出现了较明显的震荡。
为减弱滞后环节对于温度控制的不利影响,以环境箱温升模型为基础,在PID控制器中引入Smith预估补偿[16],得到的预估补偿控制结构如图13所示。
保持PID控制器参数不变,使用Smith预估补偿闭环控制结构再次对环境箱进行控制实验,此时三种控制方法的温度变化情况如图14所示。
可见,Smith预估补偿的引入有效改善了环境箱的温度控制效果,仅经历300s后环境箱内的温度即满足要求,使响应速度进一步提升,系统稳定后温度均匀度控制在2℃以内。同时,PID温度控制中的波动得到有效抑制,温升过程更加平稳。因此,采用如图13所示的环境箱温度控制策略可实现复合材料在环境箱中温度的精准补偿及控制。
4 自动化测试控制系统设计
4.1 自动送样测试系统运动学与动力学建模
自动送样系统的整体结构如图15所示,系统的运动机构主要包括电机驱动装置、气缸浮动装置和送/取样转盘。气缸浮动装置通过电磁阀进行控制,其运动方向为轴向,利用上下机械限位限定气缸极限位置,主要作用是减缓压头下压对测试系统机械结构的冲击,对驱动电机的动力传递影响不大,在传动结构的运动学和动力学分析中做忽略处理。驱动装置则用于将驱动电机的力矩传递至送/取样转盘。自动送样系统的传动结构如图16所示。
在图16所示的传动结构下,驱动电机转角与送/取样转盘转角的运动学关系如公式(7)所示。
式中,qD,qM分别为送/取样转盘和驱动电机转角,N1为电机齿轮组的减速比。同时电机与转盘的速度和加速度也符合此关系,如公式(8)和公式(9)所示。
式中,τM为电机的驱动力矩,MM,MD分别代表电机侧、送/取样转盘的转动惯量。FM,FD分别代表电机侧、送/取样转盘的转轴摩擦,其大小与转速相关,具有明显的非线性。将公式(9)带入,可化简测试系统的动力学模型如公式(11)所示。
式中,M=MM+MD/N12为测试系统的集总质量,F=FM+FD/N1为测试系统的集总摩擦力。通过公式(11)所示的动力学模型,在各参数已知的情况下即可精确获得期望的转盘加速度所需的电机驱动力矩,实现自动化测试系统的精确控制。
4.2 自动测试系统动力学参数辨识与自适应控制
完成测试系统的动力学建模后,只要获得精确的动力学参数即可精确控制送/取样转盘的运动轨迹。在实际应用中,由于转盘负载的不确定性和转轴摩擦力的高度非线性,难以预先获取系统动力学参数的真值。因此,使用具有非线性拟合能力的神经网络在线辨识系统动力学参数,并设计自适应控制律以在自动测试系统中引入自适应控制,实现控制精度的提升。
首先将辨识网络的基本结构选择为经典的三层神经网络结构,它具有输入、隐藏和输出三层结构和两层网络权值,如图17所示。在具有足够多节点时,此网络可通过对输入数据的加权处理和隐藏层的非线性映射,以任意精度实现对任意光滑连续函数的逼近[17]。
在此基本结构的基础上,构建自动测试系统动力学参数辨识的分块神经网络结构,如图18所示。它包含分别对位置的惯性力和摩擦力进行辨识的两个三层子网络,通过送/取样转盘的理想加速度及速度计算所需的驱动力矩。同时,网络权值将根据计算结果与实际的偏差进行调整,以保证网络的精确性。力矩计算和网络权值更新的公式分别设计如公式(12)和公式(13)所示。
在神经网络对未知动力学参数辨识的基础上,进一步设计自动测试系统的自适应控制方法,定义自适应控制律如公式(14)所示。
为验证此控制方法的有效性,设计自动测试系统的控制实验。实验中使用经典的PID控制方法作为对照,PID控制参数和神经网络自适应控制中的控制参数均经过良好整定,实验结果如图19所示。
从图19中实验结果可以看出,在对自动测试系统的实际控制中,基于神经网络的自适应控制方法对于理想轨迹的追踪能力明显强于传统的PID控制方法,经历了短暂的参数识别过程后就几乎与理想轨迹完全重合,而采用传统的PID控制所得的轨迹与理想轨迹则存在明显的偏差和滞后。为了更清晰的对比两种控制方法的性能差异,进一步绘制实验过程中的跟踪误差,如图20所示。
由图20可知,神经网络自适应控制在动态性能上远优于传统的PID控制,对轨迹的跟踪误差取得了更好的抑制效果,相对于传統PID控制近5°的最大跟踪误差,神经网络自适应控制中最大跟踪误差仅不足0.5°,跟踪误差的收敛性明显好于PID控制。在定位精度上,传统PID控制方法的定位误差为1°左右,神经网络自适应控制中最大定位误差接近于零,定位精度更好,可以更好的满足自动化测试要求。以上实验结果充分说明了本设计采用的神经网络自适应控制方法对提升复合材料自动送样测试系统定位精度和轨迹跟踪精度的有效性。
5 结语
(1)为改善目前人工操作模式下复合材料高温力学性能实验效率低的问题,本文设计了面向复合材料压缩测试的自动送样-测试-取样多模块测试系统,详细阐述了系统的工作原理及工作流程。
(2)针对复合材料高温力学性能测试中普遍存在的温度场控制精度低、温度滞后大的问题,构建了环境箱的三维物理模型和二维传热简化模型,通过有限元分析得到环境箱温升特性模型,在此基础上设计了高精度温度控制器,并引入Smith补偿控制方法以加快系统滞后环节补偿速度,实现了复合材料在环境箱中温度的精准补偿及控制。
(3)为提高自动化测试系统的控制精度和可靠性,使用神经网络重构系统动力学模型,完成未知动力学参数在线辨识,设计了具有强适应性、高稳定性的神经网络自适应控制器,并开展自动化测试系统的控制实验,验证了测试系统的优良控制性能。实验结果表明,相比于传统的PID控制器,神经网络自适应控制器的跟踪精度和定位精度更高,跟踪误差和定位误差均接近于零,可以更好的满足高温自动化测试要求。
(4)本文设计的复合材料高温自动化力学性能测试系统结构简单,测试效率高,温度控制精度及定位精度得到极大的提高,可助力复合材料高温力学性能自动化测试技术的进一步发展。
参 考 文 献
[1]曹春晓.一代材料技术,一代大型飞机[J].航空学报,2008(03):701-706.
[2]邢丽英,蒋诗才,周正刚.先进树脂基复合材料制造技术进展[J].复合材料学报,2013,30(02):1-9.
[3]Chen X, Li Y, Shi C, et al. The dynamic tensile properties of 2D-C/SiC composites at elevated temperatures[J]. International Journal of Impact Engineering, 2015, 79(may):75-82.
[4]Yang C P, Jiao G Q, Wang B, et al. Mechanical degradation mechanisms of 2D-C/SiC composites: Influences of preloading and oxidation[J]. Journal of the European Ceramic Society, 2015, 35(10):2765-2773.
[5]Luo Z, Zhou X, Yu J. High-temperature mechanical properties of thermal barrier coated SiC/SiC composites by PIP process with a new precursor polymer[J]. Surface & Coatings Technology, 2014, 258:146-153.
[6]Shimoda K, Hinoki T, Kishimoto H, et al. Enchanced high-temperature performances of SiC/SiC composites by high densification and crystalline structure[J]. Composites Science & Technology, 2011, 71(3):326-332.
[7]Yan K F, Zhang C Y, Qiao S R, et al. In-plane shear strength of a carbon/carbon composite at different loading rates and temperatures[J]. Materials Science & Engineering A, 2011, 528(3):1458-1462.
[8]Yan K F, Zhang C Y, Qiao S R, et al. Failure and strength of 2D-C/SiC composite under in-plane shear loading at elevated temperatures[J]. Materials & Design, 2011, 32(6):3504-3508.
[9]Wang H L, Zhang C Y, Liu Y S, et al. Temperature dependency of interlaminar shear strength of 2D-C/SiC composite[J]. Materials & Design (1980-2015), 2012, 36:172-176.
[10]Guodong, Fang, Jun, et al. High temperature fracture behavior of ZrB_2-SiC-graphite composite in vacuum and air[J]. Journal of Alloys and Compounds: An Interdisciplinary Journal of Materials Science and Solid-state Chemistry and Physics, 2015, 619:145-150.
[11]Yang H, Zhou X, Yu J, et al. Microwave and conventional sintering of SiC/SiC composites: Flexural properties and microstructures[J]. Ceramics International, 2015, 41(9): 11651-11654.
[12]Bai Y, He X, Wang R, et al. High temperature physical and mechanical properties of large-scale Ti 2 AlC bulk synthesized by self-propagating high temperature combustion synthesis with pseudo hot isostatic pressing[J]. Journal of the European Ceramic Society, 2013, 33(13-14):2435-2445.
[13]Yu H, Zhou X, Wei Z, et al. Mechanical behavior of SiCf/SiC composites with alternating PyC/SiC multilayer interphases[J]. Materials & Design, 2013, 44(FEB.):320-324.
[14]Bird M W, Aune R P, Thomas A F, et al. Temperature-dependent mechanical and long crack behavior of zirconium diboride–silicon carbide composite[J]. Journal of the European Ceramic Society, 2012, 32(12):3453-3462.
[15]韓文杰,谭文.基于PID参数整定的线性自抗扰控制参数整定[J].控制与决策,2021,36(07):1592-1600.
[16]尹成强,高洁,孙群,等.基于改进Smith预估控制结构的二自由度PID控制[J].自动化学报,2020,46(06):1274-1282.
[17]周飞燕,金林鹏,董军.卷积神经网络研究综述[J].计算机学报,2017,40(06):1229-1251.

